Ученые изучающие вопрос параллельных прямых ix век (8 видео)

История термина параллельность. Параллельность вокруг нас.

В данной работе рассматривается термин параллельность начиная с ученых разного времени

Содержание

Просмотр содержимого документа «История термина параллельность. Параллельность вокруг нас.»
Геометрия Лобачевского
Параллельные прямые
🎬 Видео

Просмотр содержимого документа
«История термина параллельность. Параллельность вокруг нас.»

Параллельность вокруг нас

Название параллельных прямых произошло от греческого слова «параллелой», которое означает «рядом идущие». Слово стало употребляться как математический термин 2500 лет назад в школе Пифагаора.

Впервые термин «параллельные прямые» возник в книге «Начала», автором которой является древнегреческий математик Евклид. Определение параллельных прямых

Евклид(3 век до н.э.), в трудах «Начала»: «Параллельные суть прямые, которые находясь в одной плоскости и будучи продолжены в обе стороны неограниченно ни с той , ни с другой стороны между собой не встречаются».

Посидоний (1 век до н.э.).

« Две прямые, лежащие в одной плоскости, равноотстоящие друг от друга».

Древнегреческий ученый Папп( вторая половина 3 века до н.э.) ввел символ параллельности прямых. Впоследствии английский экономист Рикардо (1772-1823) этот символ использовал как знак равенства. Только в 18 веке стали использовать символ.

Практические способы построения

В жизни мы часто встречаем параллельные линии, не всегда задумываясь, каким способом их получить.

Можно строить параллельные прямые с помощью имеющихся в наличии инструментов. Самый простой инструмент для построения параллельных прямых — простая линейка и угольник.

Угольник передвигаем вдоль линейки и карандашом проводим прямые, которые будут параллельны между собой.

Инструменты, используемые на практике при построении

Рейсшина – чертежный прибор для проведения параллельных линий, который состоит из линейки с поперечной планкой. Промышленность выпускает различные виды рейсшин. Здесь пример конструкторской рейсшины обычной деревянной. При помощи рейсшины можно проводить горизонтальные параллельные прямые, а при помощи рейсшины или линейки и угольника можно без труда вычерчивать и вертикальные, и наклонные параллельные прямые.

Малка — инструмент для перенесения угловых размеров при разметке деталей, для построения параллельных прямых. При выполнения столярных работ для разметки параллельных прямых используется малка (две деревянные планки ,скрепленные шарниром).

В жизни мы часто встречаемся с понятием параллельности

При строительстве зданий строго учитывается понятие параллельности. Самый наглядный пример параллельности прямых — железнодорожное полотно.

Рельсы на горизонте пересекаются, но в действительности такого быть не может. Это оптическая иллюзия.

При строительстве зданий строго учитывается понятие параллельности. Параллельные линии придают улицам особую красоту и органично вписываются в пейзаж.

Лестница задает ритм движению человека.

При сервировке стола столовые приборы раскладывают строго параллельно друг другу.

Многие животные, рыбы, насекомые имеют «параллельный» окрас.

Видео:Математика это не ИсламСкачать

Геометрия Лобачевского

Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.

Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.

И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.

Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.

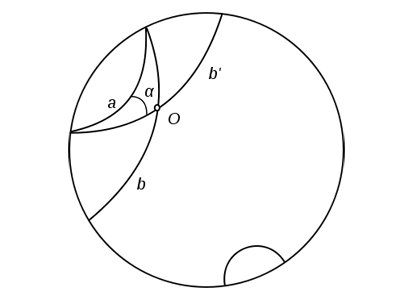
Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского выглядит следующим образом:

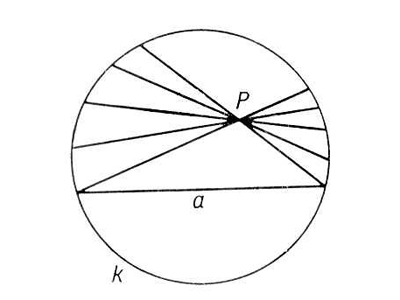
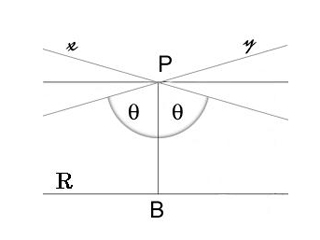
Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.

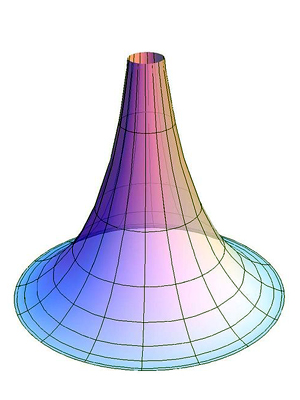
Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.

Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.

В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».

Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».

Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:

x 2 + y 2 + z 2 = c 2 t 2 ,

при делении на t 2 , то есть для скорости света, даёт уравнение сферы в пространстве с координатами v_x, v_y, v_z, которые являются составляющими скорости света по осям х, у, z.

Преобразование Лоренца сохраняет эту сферу, а поскольку они линейны, переводят прямые пространства скоростей в прямые. Из этого следует, (согласно модели Клейна) что в пространстве скоростей внутри сферы радиуса с , значит есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.

Видео:Аксиома параллельных прямых | Геометрия 7-9 класс #28 | ИнфоурокСкачать

Параллельные прямые

В «Началах» Евклида учения о параллельных излагается в одной из его 13 книг. Оно начинается с определения: «параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченном, ни стой, ни с другой стороны, между собой не встречаются».

Древнегреческий ученый Прокл, комментируя первую книгу «Начала», указывает, что еще в те времена существовали и другие определения параллельных; так, Посидоний(1 век до н. э. ) предлагает называть параллельными две прямые, лежащие в одной плоскости и равноотстоящие друг от друга. Однако! Это определение по своей сущности равносильно определению Евклида.

С развитием науки определение параллельных прямых претерпевало некоторые изменения. В современном школьном курсе геометрии параллельные определены, как прямые, лежащие в одной плоскости и не пересекающиеся.

Нам стало интересно, откуда произошел значок параллельности прямых и мы выяснили, что в III веке н. э. древнегреческий математик Папп пользовался для обозначения значком =. Так же поступал в XVIII в. после введения Рекордом знак равенства вошел в общее употребление, стали пользоваться ll , которой ввел Уильям Оутред.

Изучая теорию параллельных прямых, мы встретили термин — аксиома параллельных прямых, само слово аксиома нам знакомо(аксиома- утверждение которое не требует доказательства), поэтому нам стало интересно, какова аксиома параллельных прямых и кто ее ввел?

Этот вопрос имеет большую историю. В «Началах» Евклида содержится 5-ый постулат, из которого следует, что через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Многие математики , начиная с древних времен, предпринимали попытки доказать 5-ый постулат Евклида, т. е. вывести его из других аксиом. Однако эти попытки каждый раз оказывались неудачными. И лишь в прошлом веке было окончательно выяснено, что утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе других аксиом Евклида, а само является аксиомой. Огромную роль в решении этого непростог7о вопроса сыграл великий русский математик Н. И. Лобачевский.

Параллельные прямые очень часто встречаются в живописи. Вот один из примеров — картина Пабло Пикассо « Мужская голова».

Направление в котором выполнена эта картина- Кубизм. Этот стиль преобладал в эпоху Ренессанса. Главным направлением этого стиля является построение объемной фигуры из геометрических элементов.

Применение в архитектуре параллельных прямых очень важно и необходимо. Перед вами известные архитектурные сооружения, поглядев на которые, мы видим, что параллельные прямые здесь присутствуют.

Представьте, как бы выглядели эти знаменитые здания, если бы инженер, составляя план здания, не использовал при этом параллельные прямые. Не были бы они такими красивыми, яркими и, наверное, не смогли бы прослужить так долго.

А представьте себе, если бы рельсы не были параллельными, то они где-нибудь бы сходились и поезд претерпевал бы крушение.

А почему электрические провода параллельны? Если бы они не были параллельными, значит, соприкасаясь друг с другом, происходит замыкание, пробои, электрическая цепь размыкается и ток отключается.

Вывд один: без параллельных прямых невозможно.

На уроках геометрии мы выполняли построение с помощью угольника и линейки. Нам стало интересно существуют ли другие способы построение параллельных прямых, и некоторые из них мы вам покажем. Изобретательская мысль человечества не стоит на месте. Для построения параллельных прямых был изобретён прибор-рейсшина. Этот прибор мы смогли найти. Он состоит из линейки и цилиндра. Катая его по поверхности, можно легко построить параллельные прямые. Есть ещё одна конструкция рейсшины, которая состоит из планшета, прикреплённой к нему двигающейся линейки. ( посмотрите, как легко с помощью рейсшины можно это сделать)

2-ой способ построения параллельных прямых только с помощью одной линейки

3-ий способ именно он изучается в школьном курсе геометрии

4-ый и 5-ый способы- с помощью циркуля и линейки

Изучив вопросы по данной теме, мы подтвердили выдвинутую гипотезу и пришли к следующим выводам: а) Каждый обучающийся 7 класса должен знать историю параллельных прямых б) Параллельные прямые часто встречаются в окружающей нас жизни: в быту, в живописи, в архитектуре, при строительстве различных объектов и т. д. Параллельные прямые необходимы.

в) Умение строить параллельные прямые пригодится на практике.

Завершить выступление по данной теме мы хотим словами: « Было бы легче остановить Солнце, легче сдвинуть Землю, чем свести параллели к схождению». Надеемся, что этот проект, заинтересует кого-нибудь и пригодится при построении параллельных прямых.