У окружности бесконечно много осей симметрии (5 видео)

У окружности бесконечно много осей симметрии

Укажите номер верного утверждения.

1) Окружность имеет бесконечно много центров симметрии.

2) Прямая не имеет осей симметрии.

3) Правильный пятиугольник имеет пять осей симметрии.

4) Квадрат не имеет центра симметрии.

Проверим каждое из утверждений.

1) «Окружность имеет бесконечно много центров симметрии.» — неверно, плоская фигура обладает

центральной симметрией, если она симметрична сама себе относительно центра

2) «Прямая не имеет осей симметрии.» — неверно, прямая имеет бесконечное число осей симметрии.

3) «Правильный пятиугольник имеет пять осей симметрии.» — верно, каждая ось симметрии любого правильного многоугольника с нечетным числом сторон проходит через вершину и середину противоположной стороны.

4) «Квадрат не имеет центра симметрии.» — неверно, центр симметрии квадрата является точка пересечения диагоналей.

Содержание

Симметрия окружности
Сколько осей симметрии у круга?
Круг и окружность
Что такое ось симметрии?
Валы симметрии круга
💥 Видео

Видео:Осевая симметрия. 6 класс.Скачать

Симметрия окружности

Есть ли симметрия в окружности? Сколько осей симметрии имеет окружность? Что является центром симметрии окружности?

Окружность имеет бесконечно много осей симметрии.

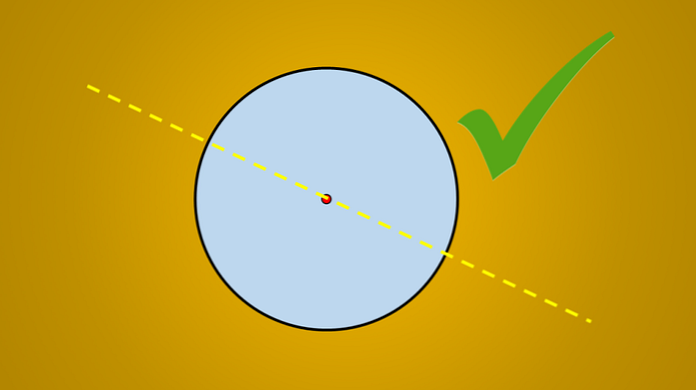
Осью симметрии окружности является любая прямая, содержащая диаметр окружности.

Проведём произвольный диаметр AB окружности.

Отметим на окружности произвольную точку X.

Из точки X проведём хорду, перпендикулярную диаметру.

Обозначим точки пересечения этой прямой с диаметром AB как P и X1.

Так как хорда перпендикулярна диаметру, то диаметр проходит через середину.

Следовательно, XP=X1P, а значит, точка X1 симметрична точке X относительно прямой, содержащей диаметр AB.

Имеем: точка, симметричная произвольной точке окружности относительно произвольного диаметра, также принадлежит окружности. Следовательно, любой диаметр окружности является её осью симметрии.

Что и требовалось доказать .

Окружность — центрально-симметричная фигура.

Осью симметрии окружности является её центр.

Отметим на окружности произвольную точку X.

Проведем через точку X диаметр XX1.

XO=X1O (как радиусы).

Таким образом, точка, симметричная произвольной точке окружности относительно её центра, также принадлежит окружности. Значит, окружность — центрально-симметричная фигура, а центр симметрии окружности — это центр окружности.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Сколько осей симметрии у круга?

оси симметрии круга Они бесконечны. Эти оси делят любую геометрическую форму на две точно равные половины.

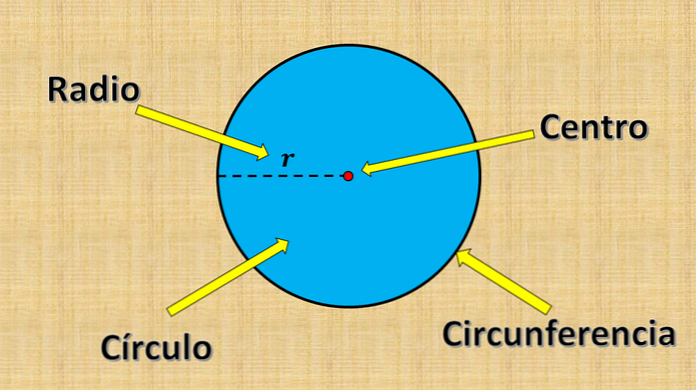
И круг состоит из всех точек, чье расстояние до фиксированной точки меньше или равно некоторому значению «r».

Упомянутая выше фиксированная точка называется центром, а значение «r» называется радиусом. Радиус — это наибольшее расстояние, которое может быть между точкой на окружности и центром..

С другой стороны, любой отрезок, концы которого находятся на краю окружности (окружности) и проходит через центр, называется диаметром. Его измерение всегда равно удвоенному радиусу.

Видео:Ось симметрииСкачать

Круг и окружность

Не путайте круг с кругом. Окружность относится только к точкам, которые находятся на расстоянии «r» от центра; то есть только край круга.

Однако при поиске осей симметрии безразлично, работаете ли вы с кругом или с кругом.

Видео:ОКРУЖНОСТЬ (симметрия в окружности) ЧАСТЬ 18Скачать

Что такое ось симметрии?

Ось симметрии — это линия, которая делит на две равные части определенную геометрическую фигуру. Другими словами, ось симметрии действует как зеркало.

Видео:Оси симметрии прямоугольника, равнобедренного треугольника, окружностиСкачать

Валы симметрии круга

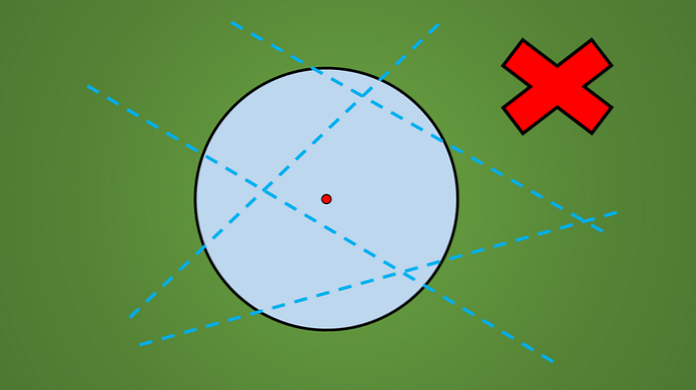
Если вы наблюдаете любой круг, независимо от его радиуса, вы можете видеть, что не каждая линия, которая пересекает его, является осью симметрии..

Например, ни одна из линий, нарисованных на следующем рисунке, не является осью симметрии..

Простой способ проверить, является ли линия осью симметрии или нет, состоит в том, чтобы перпендикулярно отразить геометрическую фигуру к противоположной стороне линии..

Если отражение не соответствует исходному рисунку, то эта линия не является осью симметрии. Следующее изображение иллюстрирует эту технику.

Но если рассматривается следующее изображение, хорошо известно, что нарисованная линия является осью симметрии круга.

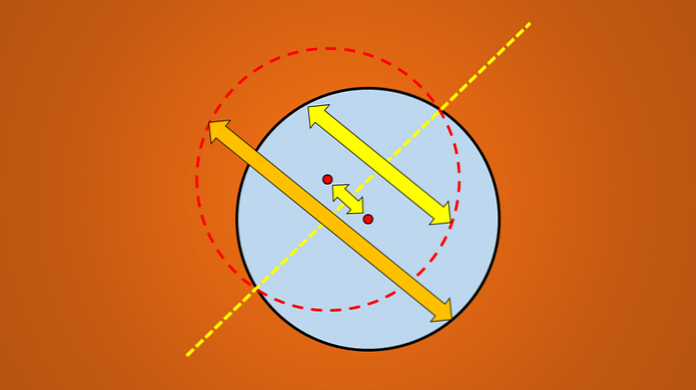
Вопрос: есть ли еще оси симметрии? Ответ — да. Если повернуть эту линию на 45 ° против часовой стрелки, полученная линия также является осью симметрии круга.

То же самое происходит, если вы поворачиваете на 90 °, 30 °, 8 ° и вообще на любое количество градусов.

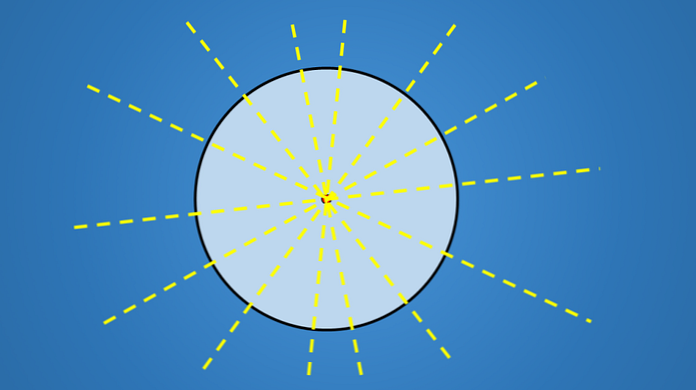
Важной особенностью этих линий является не склонность, которую они имеют, но все они проходят через центр круга. Следовательно, любая линия, содержащая диаметр окружности, является осью симметрии..

Таким образом, поскольку круг имеет бесконечное число диаметров, то он имеет бесконечное количество осей симметрии.

Другие геометрические фигуры, такие как треугольник, четырехугольник, пятиугольник, шестиугольник или любой другой многоугольник, имеют конечное число осей симметрии.

Причина, по которой круг имеет бесконечное число осей симметрии, заключается в том, что у него нет сторон.