Центры вписанной и описанной окружности совпадают верно или нет

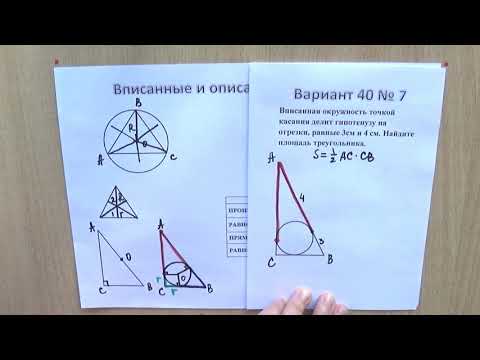
Укажите номера верных утверждений.

1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

2) Существует квадрат, который не является ромбом.

3) Сумма углов любого треугольника равна 180° .

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Центры вписанной и описанной окружностей равностороннего треугольника совпадают» — верно, т. к. совпадают точки пересечения биссектрис и серединных перпендикуляров этого треугольника.

2) «Существует квадрат, который не является ромбом» — неверно; верным будет утверждение: «Существует ромб, который не является квадратом».

3) «Сумма углов любого треугольника равна 180°» — верно по свойству треугольника.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Описанная окружность

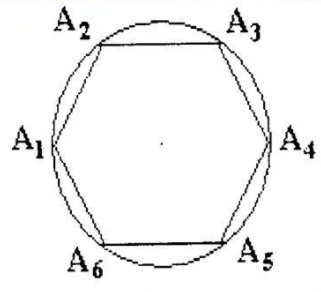
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Вписанная окружность

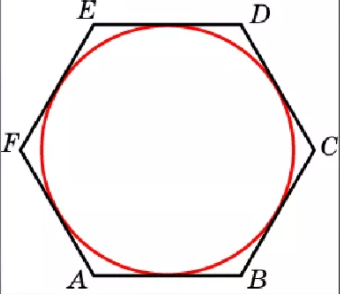
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 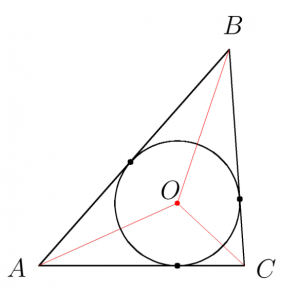Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

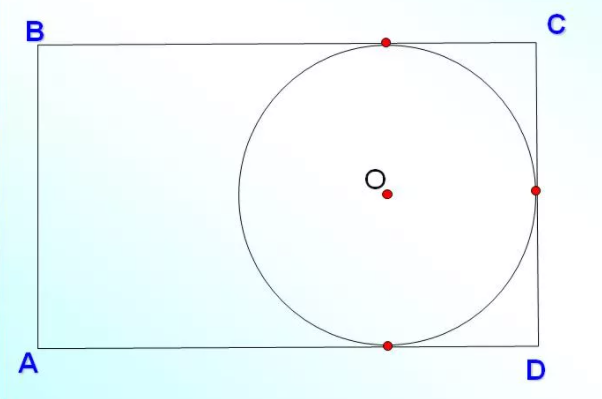
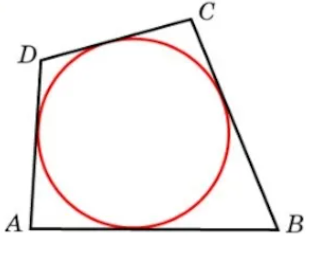
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Укажите номера верных утверждений 1)Центры вписанной и описанной окружности равностороннего треугольника совпадают?

Геометрия | 5 — 9 классы

Укажите номера верных утверждений 1)Центры вписанной и описанной окружности равностороннего треугольника совпадают.

2)Существует квадрат, который не является ромбом.

3)Сумма углов остроугольного треугольника равна 180.

Решение в скане.

Видео:Геометрия 8 класс. Тема: "Вписанная и описанная окружности. Решение задач"Скачать

Укажите в ответе номера верных утверждений : 1 )центром вписанной окружности треугольника является точка пересечения его высот ?

Укажите в ответе номера верных утверждений : 1 )центром вписанной окружности треугольника является точка пересечения его высот .

2)центром вписанной окружности треугольника является точка пересечения его медиан.

3) центром вписанной окружности является точка пересечения его биссектрис .

4)центром описанной окружности треугольника является точка пересечения его высот.

5) центром описанной окружности треугольника является точка пересечения его медиан .

6) центром описанной окружности треугольника является точка пересечения его биссектрис.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Выберите верное утверждение?

Выберите верное утверждение.

1 Сумма углов остроугольного треугольника равна 180 градусов.

2 Существует такой квадрат, который не является ромбом.

3 Центры вписанной и описанной окружностей равностороннего треугольника не совпадают.

Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Укажите номер верного утверждения?

Укажите номер верного утверждения.

1) Сумма длин катетов прямоугольного треугольника равна длине его гипотенузы.

2) Все равнобедренные треугольники подобны между собой.

3) В произвольный параллелограмм нельзя вписать окружность.

4) Радиус окружности, вписанной в равносторонний треугольник, в 2 раза меньше радиуса окружности, описанной вокруг него.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Укажите номера верных утверждений?

Укажите номера верных утверждений.

1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.

2) Существует параллелограмм, который не является прямоугольником.

3) Сумма углов тупоугольного треугольника равна 180°.

Видео:Радиус описанной окружностиСкачать

Помогите найти верное утверждение Укажите в ответ номера верных утверждений 1) если два угла трапеции равны, то трапеция равнобедренная?

Помогите найти верное утверждение Укажите в ответ номера верных утверждений 1) если два угла трапеции равны, то трапеция равнобедренная.

2) если один из углов равнобедренного треугольника острый, то и остальные его углы острые.

3) любой вписанный угол окружности равен половине любого ее центрального угла.

4) центром окружности, описанной около прямоугольного треугольника, является середина одного из его катетов.

5) около любого ромба можно описать окружность.

6) в любой пряоугольник можно вписать окружность.

7) если один из углов параллелограмма прямой, то и остальные его углы прямые.

Видео:Все о вписанных и описанных окружностях с нуля | PARTAСкачать

Укажите номера верных утверждений 1?

Укажите номера верных утверждений 1.

В правильном шестиугольнике все диагонали равны 2.

Центры вписанной и описанной около равнобедренного треугольника окружностей совпадают 3.

Если сумма двух внешних углов треугольника при двух разных вершинах равна 270 градусов то этот треугольник прямоугольный.

Видео:Вписанные и описанные окружности. Задание №16 | PARTA МАТЕМАТИКА ОГЭ 2023Скачать

Укажите номера верных утверждений1?

Укажите номера верных утверждений

Диагонали квадрата перпендикулярны

Сумма углов в ромбе равна 180 градусам

Медиана в любом треугольнике является высотой

Если в треугольнике катеты равны он является равносторонним.

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Укажите номера верных утверждений?

Укажите номера верных утверждений.

1) Любой квадрат является ромбом

2) Против равных сторон треугольника лежат равные углы.

3)через любую точку, лежащую вне окружности, можно провести касательные к этой окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Укажите номера верных утверждений 1)существует треугольник с внутренними углами 26, 73, 81?

Укажите номера верных утверждений 1)существует треугольник с внутренними углами 26, 73, 81.

2)В любом ромбе диагонали равны 3)Центром описанной окружности является точка пересечения медиан этого треугольника.

4)Сторона и 2 определенных угла треугольника однозначно определяют этот треугольник.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Укажите номера верных утверждений?

Укажите номера верных утверждений.

1. Сумма углов треугольника меньше 180 градусов.

2. У остроугольного треугольника все углы острые.

3. Существует треугольник, у которого углы равно 100 градусов, 30, 50.

4. Внешний угол треугольника может быть меньше, любого внутреннего угла этого треугольника.

Вопрос Укажите номера верных утверждений 1)Центры вписанной и описанной окружности равностороннего треугольника совпадают?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

2x + 5x + 2x + 5х = 42 14x = 42 x = 42÷14 x = 3 6 см одна сторона 15 см вторая.

Проведём высоту АК⊥ВС. В равнобедренном тр — ке высота АК является медианой. ВК = СК = ВС / 2 = 6 / 2 = 3 см. В прямоугольном тр — ке ВАК АК² = АВ² — ВК² = 5² — 3² = 16, АК = 4 см — это ответ. АД⊥АВС⇒ АД⊥ВС, АК⊥ВС, значит по теореме о трёх перпен..

Трапеция, ее признаки и свойства Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами. . Средняя линия трапеции — отрезок..

Решение в приложении.

Мама за 30 минут прошла 2, 5 км, Юра проехал 6 км. Имеем прямоугольный треугольник с катетами 2, 5 и 6 км. Надо найти гипотенузу. С² = 2, 5² + 6² = 6, 25 + 36 = 72, 25 с = √72, 25 = 8, 5 Ответ : 8, 5 км.

Вот 180 — (65 + 50) = 65 и т. Д На фото.

По — моему, есть ошибка в вопросе.

Пусть х — один из смежных углов, тогда второй угол 180 — х. Биссектриса первого угла — х / 2, второго — (180 — х) / 2 = 90 — (x / 2). Т. к. Биссектрисы выходят из одной точки то угол между ними равен (х / 2) + 90 — (х — 2) = 90. Следовательно, би..

📸 Видео

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

8 класс, 38 урок, Вписанная окружностьСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанная и описанная окружности. ЗадачиСкачать

Задание 1. Профильный ЕГЭ 2023. Вписанная и описанная окружность.Скачать

Вписанные и описанные окружностиСкачать