Геометрия | 10 — 11 классы
Центр вписанной окружности делит высоту равнобедренного треугольника, опущенную на основание, на отрезки 5 см и 3 см, считая от вершины.
Определите длину основания треугольника.
Пусть окружность вписана в треугольник АВС.
ВН — высота, биссектриса и медиана треугольника АВС.
ВН = ВО + ОН = 5_3 = 8 см
К — точка касания окружности и боковой стороны.
В прямоугольном треугольнике ВКО ВК = 4 ( треугольник — египетский, можно проверить по т.
Треугольники ВНС и ВКО — подобны( прямоугольные с общим острым углом при В).
АС = 2 * 6 = 12 см.
- Боковая сторона равнобедренного треугольника равна 10, а основание 16?
- Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см?
- В равнобедренный треугольник вписали окружность?
- Высота равнобедренного тр — ка опущенная на боковую сторону делит её на отрезки длиной 4 см и 16 см считая от вершины угла при основании?
- Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту, проведенную к основанию, в отношение 5 : 3?
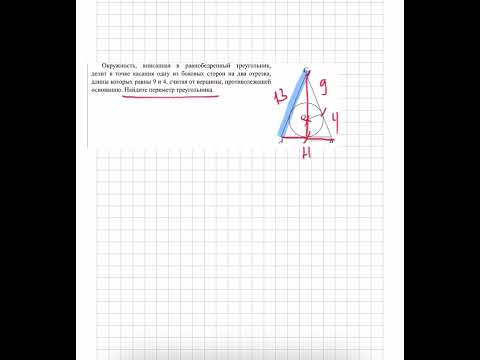
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию?
- Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см ; основание треугольника 12 см?
- 1) Вычислите периметр равнобедренного треугольника , если окружность, вписанная в треугольник , точкой касания делит его боковую сторону на отрезки длиной 4см и 5см, считая от основания?
- В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см?
- Основание AC равнобедренного треугольника ABC равно 12?
- Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту
- Как написать хороший ответ?
- Окружность, вписанная в треугольник. Теоремы и их рассмотрение
- Окружность, вписанная в равнобедренный треугольник
- Окружность, вписанная в прямоугольный треугольник
- Формулировка теоремы о вписанной окружности
- Теорема о центре окружности, вписанной в треугольник
- 📺 Видео
Видео:Геометрия Центр окружности, вписанной в равнобедренный треугольник, делит его высоту, проведеннуюСкачать

Боковая сторона равнобедренного треугольника равна 10, а основание 16?
Боковая сторона равнобедренного треугольника равна 10, а основание 16.
На какие отрезки делятся высота треугольника, опущенной из вершины, биссектрисой угла при основании?
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см?
Найдите основание равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60 см.
Видео:Геометрия К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 смСкачать

В равнобедренный треугольник вписали окружность?
В равнобедренный треугольник вписали окружность.
Точка касания делит боковую сторону треугольника на отрезки длиной 12 см и 6 см , считая от основания.
Вычислите периметр треугольника.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Высота равнобедренного тр — ка опущенная на боковую сторону делит её на отрезки длиной 4 см и 16 см считая от вершины угла при основании?
Высота равнобедренного тр — ка опущенная на боковую сторону делит её на отрезки длиной 4 см и 16 см считая от вершины угла при основании.
Найти основание тр — ка.
Видео:№690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружностиСкачать

Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту, проведенную к основанию, в отношение 5 : 3?
Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту, проведенную к основанию, в отношение 5 : 3.
Найдите радиус описанной окружности, если высота, проведенная к основанию равна 32 см.
Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
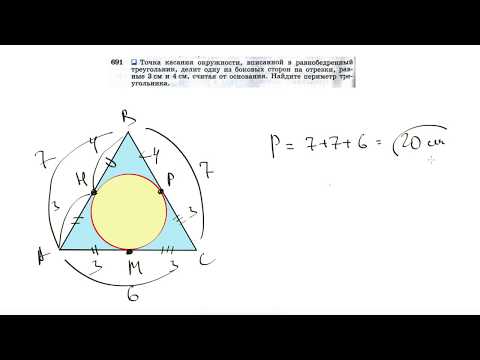
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию?
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию.
Найдите периметр треугольника.
Видео:Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторонСкачать
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см ; основание треугольника 12 см?
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см ; основание треугольника 12 см.
Найти площадь этого треугольника.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

1) Вычислите периметр равнобедренного треугольника , если окружность, вписанная в треугольник , точкой касания делит его боковую сторону на отрезки длиной 4см и 5см, считая от основания?
1) Вычислите периметр равнобедренного треугольника , если окружность, вписанная в треугольник , точкой касания делит его боковую сторону на отрезки длиной 4см и 5см, считая от основания.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см?
В равнобедренном треугольнике центр вписанной окружности делит высоту в отношении 17 : 15, а боковая сторона равна 34 см.
Найдите основание треугольника.
Видео:ЕГЭ Математика Задание 6#27935Скачать

Основание AC равнобедренного треугольника ABC равно 12?
Основание AC равнобедренного треугольника ABC равно 12.
Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.
Найдите радиус окружности, вписанной в треугольник ABC.
Сторона ромба равна 32, а острый угол равен 60°.
Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка.
Каковы длины этих отрезков?
Вы открыли страницу вопроса Центр вписанной окружности делит высоту равнобедренного треугольника, опущенную на основание, на отрезки 5 см и 3 см, считая от вершины?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту
Вопрос по геометрии:
Центр вписанной в остроугольный равнобедренный треугольник окружности делит высоту, проведенную к основанию, в отношение 5:3. Найдите радиус описанной окружности, если высота, проведенная к основанию равна 32 см
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Сделаем и рассмотрим рисунок.
Т.к. высота делится на отрезки с отношением 5:3, вся высота содержит 8 частей, и одна часть равна 32:8=4.
Тогда
r=ОН=4*3=12 см
ВО=4*5=20 см
Проведя радиус ОР в точку касания окружности и боковой стороны, получим прямоугольный треугольник ВРО.
По т. Пифагора
ВР=√(ВО²-ОР²)=16 см
Треугольники ВРО и ВНС подобны — оба прямоугольные и имеют общий острый угол при вершине В.
Коэффициент их подобия k=ВН:ВР=32:16=2 ⇒
ВС=ВО*2=40 см
СР=ОР*2=24 см.
Высота равнобедренного треугольника еще и медиана. ⇒
АС=48
R=abc:4S
S, найденная по формуле Герона, равна 768 ( вычисления приводить нет нужды, при желании можно их проверить)
R=40*40*48:(4*768)=25 см
———
[email protected]
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Окружность, вписанная в треугольник. Теоремы и их рассмотрение
Еще в Древнем Египте появилась наука, с помощью которой можно было измерять объемы, площади и другие величины. Толчком к этому послужило строительство пирамид. Оно предполагало значительное число сложных расчетов. И кроме строительства, было важно правильно измерить землю. Отсюда и появилась наука «геометрия» от греческих слов «геос» — земля и «метрио» — измеряю.
Исследованию геометрических форм способствовало наблюдение астрономических явлений. И уже в 17-м веке до н. э. были найдены начальные способы расчета площади круга, объема шара и главнейшее открытие — теорема Пифагора.

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:
В треугольник можно вписать только одну окружность.
При таком расположении окружность — вписанная, а треугольник — описанный около окружности.
Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:
Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.
Видео:Центр описанной окружности равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Окружность, вписанная в равнобедренный треугольник
Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.
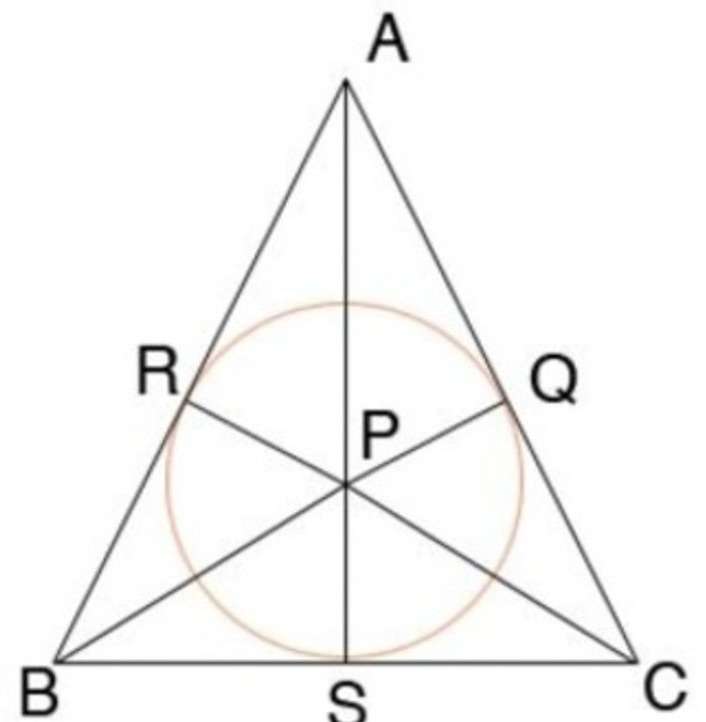
На фото ниже показана окружность, находящаяся внутри равнобедренного треугольника. Условие теоремы об окружности, вписанной в треугольник, соблюдено — она касается всех сторон треугольника AB, ВС И СА в точках R, S, Q соответственно.
Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).
Свойства теоремы об окружности, вписанной в треугольник:
- Отрезки, выходящие из одной вершины треугольника к точкам касания с окружностью, равны. На рисунке AR = AQ, BR = BS, CS = CQ.
- Радиус окружности (вписанной) — это площадь, деленная на полупериметр треугольника. Как пример, нужно начертить равнобедренный треугольник с теми же буквенными обозначениями, что на картинке, следующих размеров: основание ВС = 3 см, высота AS = 2 см, стороны АВ=ВС, соответственно, получаются по 2,5 см каждая. Проведем из каждого угла биссектрису и место их пересечения обозначим как Р. Впишем окружность с радиусом PS, длину которого нужно найти. Узнать площадь треугольника можно, умножив 1/2 основания на высоту: S = 1/2 * DC * AS = 1/2 * 3 * 2 = 3 см2. Полупериметр треугольника равен 1/2 суммы всех сторон: Р = (АВ + ВС + СА) / 2 = (2,5 + 3 + 2,5) / 2 = 4 см; PS = S/P = 3/4 = 0,75 см2, что полностью соответствует действительности, если измерить линейкой. Соответственно, верно свойство теоремы об окружности, вписанной в треугольник.
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

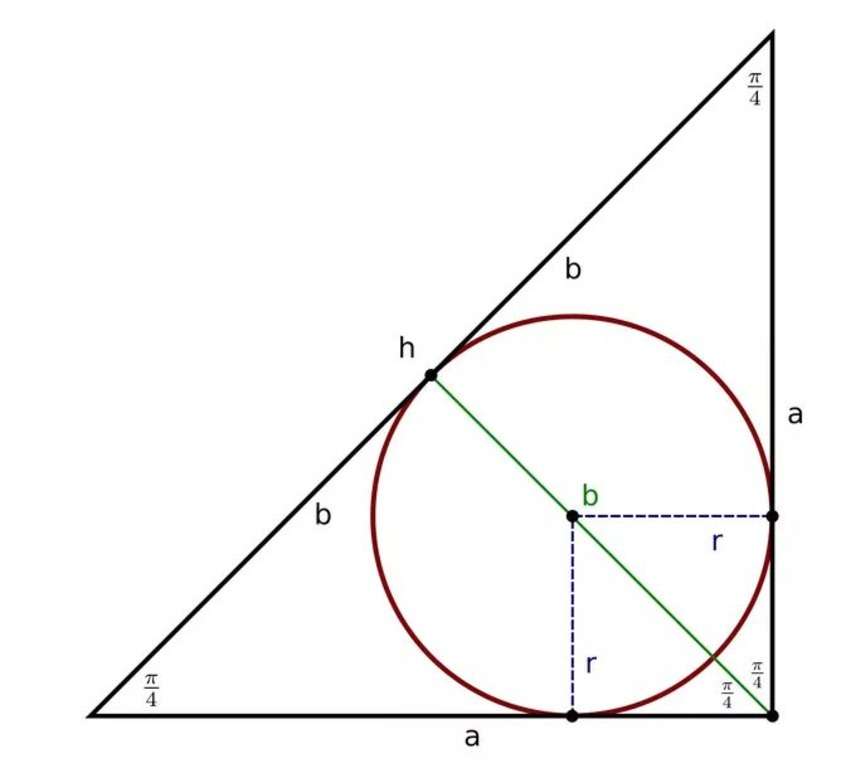
Окружность, вписанная в прямоугольный треугольник
Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.
Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.
Есть хорошая формула, которая поможет высчитать площадь треугольника — периметр умножить на радиус вписанной в этот треугольник окружности.
Видео:Построить описанную окружность (Задача 1)Скачать

Формулировка теоремы о вписанной окружности
В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:
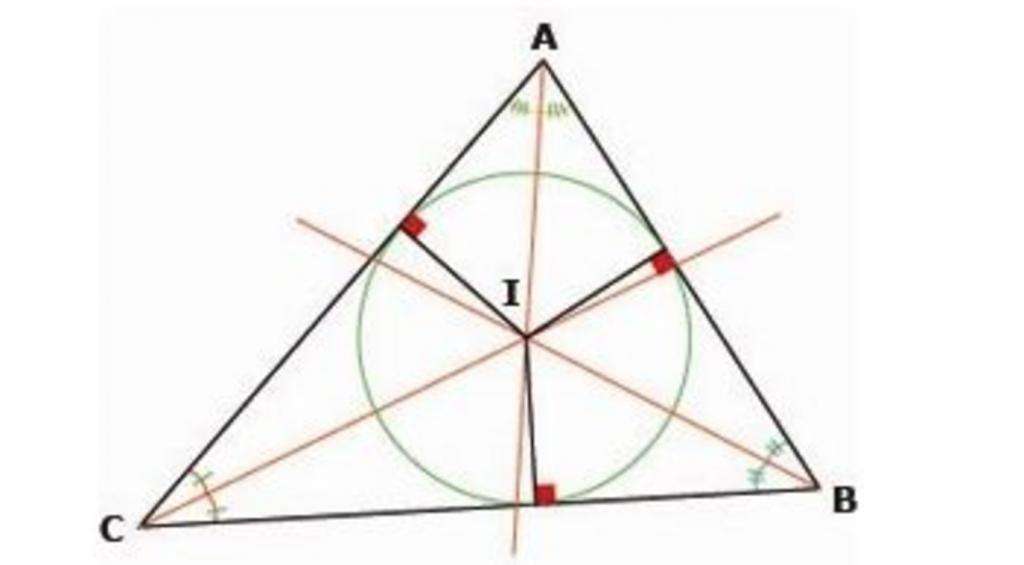
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.
На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.
Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Теорема о центре окружности, вписанной в треугольник
Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.
Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.
📺 Видео
2065 радиус окружности вписанной в правильный треугольник равен 29 Найдите высоту этого треугольникаСкачать

Равносторонний треугольник в окружностиСкачать

Задание 24 Площадь вписанного равнобедренного треугольникаСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать