Центр описанной окружности совпадает с точкой пересечения его

Геометрия | 1 — 4 классы

Центр описанной около треугольника окружности совпадает с точкой пересечения его.

Теорема о центре окружности, описанной около треугольника :

Центром описанной около треугольника окружности является точка пересечения его серединных перпендикуляров.

Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

Видео:Задание 3 ЕГЭ по математике. Урок 72Скачать

Диаметр окружности, описанной около прямоугольного треугольника, равен 18 см?

Диаметр окружности, описанной около прямоугольного треугольника, равен 18 см.

Найдите гипотенузу треугольника.

Где расположен центр окружности?

Видео:Построить описанную окружность (Задача 1)Скачать

Точка О – центр окружности, описанной около треугольника АВС?

Точка О – центр окружности, описанной около треугольника АВС.

Принадлежит ли точка С плоскости, в которой лежат точки А, В и О?

Видео:Задание 3 ЕГЭ по математике. Урок 70Скачать

Докажите, что если высота треугольника проходит через центр описанной около него окружности, то этот треугольник равнобедренный?

Докажите, что если высота треугольника проходит через центр описанной около него окружности, то этот треугольник равнобедренный.

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Центры вписанной и описанной около равностороннего треугольника окружностей совпадают?

Центры вписанной и описанной около равностороннего треугольника окружностей совпадают.

Доказать, что при этом радиус описанной окружности в 2 раза больше радиуса вписанной.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В равностороннем треугольнике проведены две медианы?

В равностороннем треугольнике проведены две медианы.

Является ли точка пересечения медиан центром окружности описанной около этого треугольника.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Помогите, пожалуйста?

Докажите, что если центр окружности, описанной около треугольника, принадлежит его высоте, то этот треугольник равнобедренный .

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Треугольник АВС равносторонний?

Треугольник АВС равносторонний.

Докажите, что центр описанной около этого треугольника окружности совпадает с центром вписанной в этот треугольник окружности.

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Около равнобедренного треугольника авс описана окружность с центром о?

Около равнобедренного треугольника авс описана окружность с центром о.

Найдите угол вао.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Около окружности с центром в точке О описан треугольник авс стороны которого равны 9, 10 и 11?

Около окружности с центром в точке О описан треугольник авс стороны которого равны 9, 10 и 11.

Найдите длины отрезков , на которые стороны треугольника делятся точками касания с окружностью.

Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

С решкнием пожалуйста 1)Центр вписанной в треугольник окружности совпадает с точкой пересечения его …а) медианб) биссектрисв) серединных перпендикуляров2)Центр вписанной в треугольник окружности равно?

С решкнием пожалуйста 1)Центр вписанной в треугольник окружности совпадает с точкой пересечения его …

в) серединных перпендикуляров

2)Центр вписанной в треугольник окружности равноудален от …

в) вершин треугольника

3)Центр вписанной в треугольник окружности является точкой пересечения его медиан.

Видео:Задание 3 ЕГЭ по математике. Урок 71Скачать

Дать определение вписанной и описанной окружности (указать где лежит центр окружности , вписанный в треугольник, и описанный около треугольника)?

Дать определение вписанной и описанной окружности (указать где лежит центр окружности , вписанный в треугольник, и описанный около треугольника).

На этой странице находится вопрос Центр описанной около треугольника окружности совпадает с точкой пересечения его?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 1 — 4 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

1 — I, 2 — II, 3 — III, 4 — IV, 5 — V, 6 — VI, 7 — VII, 8 — VIII, 9 — VIIII, 10 — X.

Это и есть арабские.

У меня так получилось.

1)x — 1 угол 14х — второй угол 14х + х = 180 15х = 180 х = 12 1 угол — 12 2 угол — 12 * 14 = 168.

. это первый номер.

Определиния дашь из учебника, найдешь.

Задача решается легко. Так как АС — основание то углы ВАС и ВСА равны, т. Е. уголВСА = ВАС = 50градусам. Так как АД — биссектриса, то угол А делим пополам(50 : 2 = 25градусов) — угол ДАС. Мы знаем что углы треугольника в сумме дают 180градусов. ..

Точкой, равноудаленной от всех сторон треугольника, является центр вписанной окружности, которым является точка пересечения биссектрис (свойство биссектрисы, любая точка которой находится на равном расстоянии от сторон угла, между которыми проведена ..

1) N = 180 — 109 = 71 P = 180 — 37 = 143 2)∠1 = ∠2, a∠3 = ∠4 ∠1 = ∠2 = 115 ∠3 = ∠4 = (360 — 2 * 115) / 2 = 65 3)∠A = 70, ∠B = 40 ∠B = 180 — 70 = 110 ∠D = 180 — 40 = 140.

A и с угол 1 + угол 3 = 42° + 138° = 180° угол 1 и 3 — односторонние при пересечении прямых а и с секущей d. Значит, по признаку параллельности прямых : если две прямые пересечены секущей и односторонние углы составляют в сумме 180°, то прямые парал..

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Центр описанной окружности

Где находится центр описанной около треугольника окружности? Что можно сказать о центре окружности, описанной около многоугольника?

Центр описанной около треугольника окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.

окружность (O;R) — описанная около ∆ ABC.

O — точка пересечения серединных перпендикуляров к сторонам ∆ ABC.

Соединим отрезками точки O и A, O и C.

OA=OC (как радиусы), следовательно, треугольник AOC — равнобедренный с основанием AC (по определению).

По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):

Следовательно, центр описанной окружности — точка O — лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину, то есть на серединном перпендикуляре к AC.

Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.

Так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, то точка O — центр описанной около треугольника ABC окружности.

Что и требовалось доказать.

Аналогичные рассуждения можно применить и для многоугольника, около которого можно описать окружность.

Центр описанной около многоугольника окружности является точкой пересечения серединных перпендикуляров к сторонам этого многоугольника.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

2 Comments

на мой взгляд у вас опечатка — «Соединим отрезками точки O и A, O и C.

OA=OB( написано ОВ вместо ОС) (как радиусы), следовательно, треугольник AOB — равнобедренный с основанием AC (по определению).»

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Окружность, описанная около треугольника

Видео:Описанная окружность | Геометрия 7-9 класс #75 | ИнфоурокСкачать

Определение окружности, описанной около треугольника

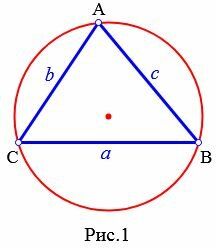
Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).

При этом треугольник называется треугольником вписанным в окружность .

Видео:8 класс, 39 урок, Описанная окружностьСкачать

Теорема об окружности, описанной около треугольника

Теорема 1. Около любого треугольника можно описать окружность.

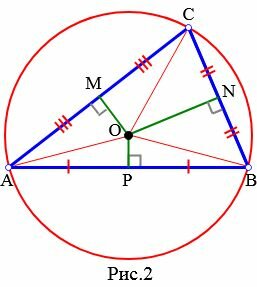Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.

Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

Замечание 1. Около любого треугольника можно описать только одну окружность.

Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.

📸 Видео

Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Точка O центр окружности описанной около остроугольного треугольникаСкачать

Изогональное сопряжение | Олимпиадная математикаСкачать

КАРАСЕВ: СБИТЫЙ "ИЛ" - ИГРА НА СРЫВ ПЕРЕГОВОРОВ? РЕШАЮЩИЙ МОМЕНТ: ВОЗДУШНАЯ ВОЙНА и "ЗАМЕРШИЙ" ФРОНТСкачать