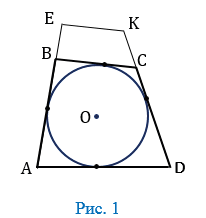
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность. На рисунке 1 четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
Теорема
| В любой треугольник можно вписать окружность. |
Доказательство
Дано: произвольный 
АВС.
Доказать: в АВС можно вписать окружность.
Доказательство:
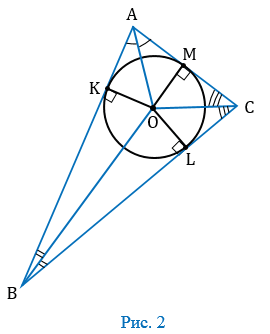
1. Проведем биссектрисы углов А, В и С, которые пересекутся в точке О (следствие из свойства биссектрис). Из точки О проведем перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА (Рис. 2).
2. Точка О равноудалена от сторон АВС (свойство биссектрис), поэтому ОК = ОL = ОМ. Следовательно, окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны АВС касаются этой окружности в точках К, L, М, т.к. они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в АВС. Теорема доказана.
Замечание 1
| В треугольник можно вписать только одну окружность. |
Доказательство
Предположим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают, значит в треугольник можно вписать только одну окружность. Что и требовалось доказать.
Замечание 2
| Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. |
Доказательство
На рисунке 2 мы видим, что АВС составлен из трех треугольников: АВО, ВСО и САО. Пусть АВ, ВС и АС основания треугольников АВО, ВСО и САО соответственно, тогда высотами данных треугольников окажутся отрезки ОК = ОL = ОМ = r ( r — радиус окружности с центром О). Следовательно, площади этих треугольников вычисляются по формулам: 
. Тогда, по свойству площадей, площадь треугольника АВС выражается формулой: 
, где 
— периметр АВС. Что и требовалось доказать.
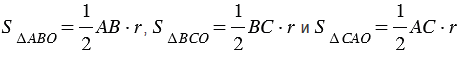
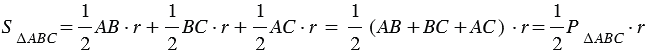
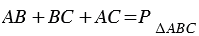
Замечание 3
| Не во всякий четырехугольник можно вписать окружность. |
Доказательство
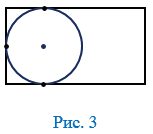
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т.е. прямоугольник, не являющийся квадратом. В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон (Рис.3), но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.к. диаметр окружности меньше большей стороны прямоугольника т.е. нельзя вписать окружность. Что и требовалось доказать.
Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
| В любом описанном четырехугольнике суммы противоположных сторон равны. |
Доказательство
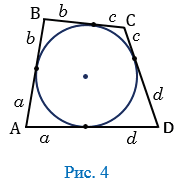
Рассмотрим четырехугольник АВСD, описанный около окружности (Рис. 4).
На рисунке 4 одинаковыми буквами обозначены равные отрезки касательных, т.к. отрезки касательных к окружности, проведенные из одной точки, равны. Тогда АВ + СD =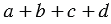 
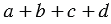
и ВС + АD = , следовательно, АВ + СD = ВС + АD.
Верно и обратное утверждение:
| Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. |
Доказательство
Пусть в выпуклом четырехугольнике АВСD
АВ + СD = ВС + АD. (1)
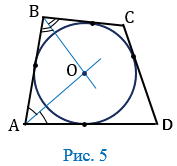
Точка О пересечения биссектрис углов А и В равноудалена от сторон АD, АВ и ВС (свойство биссектрис), поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (Рис. 5).
Докажем, что эта окружность касается также стороны СD и, значит, является вписанной в четырехугольник АВСD.
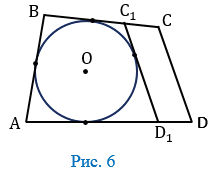
Предположим, что это не так. Тогда прямая СD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (Рис. 6). Проведем касательную С1D1, параллельную стороне СD (С1 и D1 — точки пересечения касательной со сторонами ВС и АD).
Так как АВС1D1 — описанный четырехугольник, то по свойству его противоположных сторон
АВ + С1D1 = ВС1 + AD1. (2)
Но ВС1 = ВС — С1С, АD1 = АD — D1D, поэтому из равенства (2) получаем:
С1D1 + С1С + D1D = ВС + АD — АВ.
Правая часть этого равенства в силу (1) равна СD. Следовательно, приходим к равенству
т.е. в четырехугольник С1СDD1 одна сторона равна сумме трех других сторон. Но этого не может быть, т.к. к аждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон. Значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны СD. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать
Равные хорды
Выясним, какими свойствами обладают равные хорды и равные дуги.
Равные хорды равноудалены от центра окружности.
Дано : окр. (O;R), AB и CD — хорды,
Соединим центр окружности с концами хорд.
I. Рассмотрим треугольники AOB и COD.
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.
II. Рассмотрим прямоугольные треугольники AOF и COK.
2) ∠A=∠C (по доказанному).
Из равенства треугольников следует равенство соответствующих сторон: OF=OK.
Что и требовалось доказать .
Если хорды равноудалены от центра окружности, то они равны.
Дано: окр. (O;R), AB и CD — хорды,
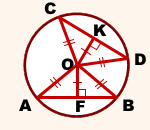
Соединим центр окружности с концами хорд.
I. Рассмотрим прямоугольные треугольники OKD и OFB.
1)OF=OK (по условию)
2)OD=OB (как радиусы).
Из равенства треугольников следует равенство соответствующих сторон:
II. Рассмотрим треугольники AOB и COD.
Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.
По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.
Что и требовалось доказать.
Равные хорды стягивают равные дуги.
Дано : окр. (O;R), AB и CD — хорды, AB=CD,
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.
Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD
Что и требовалось доказать .
Хорды, стягивающие равны дуги, равны.
Дано: окр. (O;R), AB и CD — хорды,
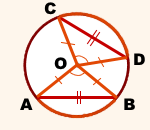
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.
Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.
Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать
Центр окружности равноудален от сторон
554. Докажите, что если центр окружности, описанной около треугольника, принадлежит его высоте, то этот треугольник равнобедренный.
555. Докажите, что если центр окружности, вписанной в треугольник, принадлежит его медиане, то этот треугольник равнобедренный.
556. Докажите, что если центры вписанной и описанной окружностей треугольника совпадают, то этот треугольник равносторонний.
557. Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 7 : 5, считая от вершины треугольника. Найдите стороны треугольника, если его периметр равен 68 см.
558. Периметр треугольника ABC , описанного около окружности, равен 52 см. Точка касания со стороной AB делит эту сторону в отношении 2 : 3, считая от вершины A . Точка касания со стороной BC удалена от вершины C на 6 см. Найдите стороны треугольника.
559. В треугольник с углами 30°, 70° и 80° вписана окружность. Найдите углы треугольника, вершины которого являются точками касания вписанной окружности со сторонами данного треугольника.
560. Окружность, вписанная в равнобедренный треугольник ABC , касается его боковых сторон AB и BC в точках M и N соответственно. Докажите, что MN ‖ AC .
561. Докажите, что если центр окружности, описанной около треугольника, принадлежит его стороне, то этот треугольник — прямоугольный.
562. В треугольник ABC вписана окружность, касающаяся стороны AB в точке M , BС = a . Докажите, что AM = p — a , где p — полупериметр треугольника ABC .
563. К окружности, вписанной в равносторонний треугольник со стороной a , провели касательную, пересекающую две его стороны. Найдите периметр треугольника, который эта касательная отсекает от данного.
564. В равнобедренный треугольник ABC ( AB = BC ) с основанием 10 см вписана окружность. К этой окружности проведены три касательные, отсекающие от данного треугольника треугольники ADK , BEF и CMN . Сумма периметров этих треугольников равна 42 см. Чему равна боковая сторона данного треугольника?
565. В треугольнике ABC отрезок BD — медиана, AB = 7 см, BC = 8 см. В треугольники ABD и BDC вписали окружности. Найдите расстояние между точками касания этих окружностей с отрезком BD .
566. Каждый из углов BAC и ACB треугольника ABC разделили на три равные части (рис. 308). Докажите, что ∠ AMN = ∠ CMN .
567. Пусть вершина угла B недоступна (рис. 309). С помощью транспортира и линейки без делений постройте прямую, содержащую биссектрису угла B .
568. Точки F и O — центры вписанной и описанной окружностей равнобедренного треугольника ABC соответственно (рис. 310). Они находятся на одинаковом расстоянии от его основания AC . Найдите углы треугольника ABC .
Упражнения для повторения
569. Биссектриса угла ABC образует с его стороной угол, равный углу, смежному с углом ABC . Найдите угол ABC .
570. В равнобедренном треугольнике из вершины одного угла при основании провели высоту треугольника, а из вершины другого угла при основании — биссектрису треугольника. Один из углов, образовавшихся при пересечении проведённых биссектрисы и высоты, равен 64°. Найдите углы данного треугольника.
571. На рисунке 311 BC ‖ AD , AB = 3 см, BC = 10 см. Биссектриса угла BAD пересекает отрезок BC в точке K . Найдите отрезки BK и KC .
572. В треугольнике ABC известно, что AB = BC , AM и CK — медианы этого треугольника. Докажите, что MK ‖ AC .
Наблюдайте, рисуйте, конструируйте, фантазируйте
573. В квадрате ABCD вырезали заштрихованную фигуру (рис. 312). Разделите оставшуюся часть квадрата на четыре равные фигуры.
🔥 Видео
Центр окружности описанной вокруг треугольникаСкачать
#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать
Окружность и треугольникСкачать
Вписанная окружность | Геометрия 7-9 класс #74 | ИнфоурокСкачать
Точка пересечения двух окружностей равноудалена ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Вписанная окружностьСкачать
№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать
8 класс, 38 урок, Вписанная окружностьСкачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Геометрия В треугольнике ABC известны длины сторон AB = 18, AC = 36, точка O — центр окружностиСкачать
Точка O центр окружности описанной около остроугольного треугольникаСкачать
Три точки, задающие окружностьСкачать
№274. Докажите, что в равнобедренном треугольнике середина основания равноудалена от боковых сторон.Скачать
№200. Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около мноСкачать
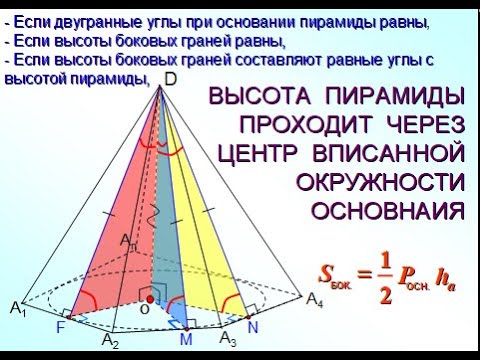
Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать
Радиус описанной окружностиСкачать
✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать
ЕГЭ Задание 16 Две касающиеся окружностиСкачать
