Тригонометрическая окружность со всеми значениями для печати скачать (5 видео)

Тригонометрический круг.

Содержание

Скачать шаблоны для тригонометрии.
Примеры.
Замечание.
mathematichka@yandex.ru
Тригонометрический круг. Основные значения тригонометрических функций
Тригонометрический круг: вся тригонометрия на одном рисунке
А теперь подробно о тригонометрическом круге:
🌟 Видео

Видео:Тригонометрическая окружность для непонимающихСкачать

Скачать шаблоны для тригонометрии.

Здесь голубая сетка — линии декартовой системы координат. Масштаб — 1:10. В этом масштабе радиус окружности, равный единице, составляет 10 клеточек. sin30° = 1/2 составляет 5 клеточек, и т.п. Можно примерно (на глаз) отмечать или определять значения синусов и косинусов.
Зеленая радиальная сетка — лучи с шагом 15° или, что одно и то же, с шагом π/12. Удобно рисовать углы в радианах или градусах и ориентироваться в их величинах и расположении относительно четвертей круга.

Лучше всего использовать смешанную сетку — рисунок слева. Этот рисунок вы можете скачать себе на компьютер и распечатать на черно-белом принтере. Получится тонкая сетка линий, как бы нарисованных карандашом, поверх которой вам будет удобно делать свои чертежи для решения задач по тригонометрии. На втором рисунке показан пример использования такой смешанной сетки для того, чтобы проверить правильно ли определены значения sin(−π/3) и cos(−π/3). Остальные примеры и пояснения к ним расположены ниже.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Примеры.

4/π ≈ 4/3,14 ≈ 1,28
Значит 4 радиана это угол 1π + 0,28π. Кусочек 0,28π больше, чем π/4 = 0,25π, и меньше, чем π/3 ≈ 0,33π
Рисуем луч внутри сектора с границами π + π/4 и π + π/3. (Здесь серым шаблон — то, что получится после распечатки, фиолетовым — то, что отметите вы вручную.)

Отмечаем проекцию на вертикальную ось — ось синусов. Попали на отрицательный участок оси в 8-ю клеточку из 10-ти. Следовательно, sin4 ≈ −8/10 = −0,8.
Для сравнения — с помощью калькулятора получим ответ −0,7568.

Те, кто лучше ориентируется при измерении углов в градусах, могут вспомнить, что 1 радиан равен приблизительно 57,3 градуса. Соответственно, 4 рад ≈ 229º. Попробуйте самостоятельно начертить этот луч на круге.

Пример 2. Требуется убедиться, что правильно запомнились табличные значения тригонометрических функций для характерных («геометрических») углов.

Вспоминаем, что:
1/2 = 0,5 = 5/10 – пять клеток от центра окружности;
√2 _ /2 ≈ 1,4142/2 = 0,707 ≈ 7/10 – семь клеток от центра окружности (чуть дальше, чем граница седьмой клетки);
√3 _ /2 ≈ 1,7321/2 = 0,866 ≈ 8,7/10 – чуть дальше, чем середина девятой клетки.
Отмечаем значения синусов и косинусов на синей сетке, значения углов — на зелёной.
Совмещаем обе сетки. Если всё правильно, то в результате получатся картинки, аналогичные следующим.

Замечание.

Не забывайте – значения синусов и косинусов любых углов по абсолютной величине не превышают 1. Если вы пытаетесь записать в ответ большее число, то ищите ошибку. Возможно, вы пишите ответ в клеточках, а не в заданных единицах?

mathematichka@yandex.ru

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Внимание, © mathematichka. Копирование рисунков на других сайтах запрещено. Ставьте ссылку.

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Тригонометрический круг. Основные значения тригонометрических функций

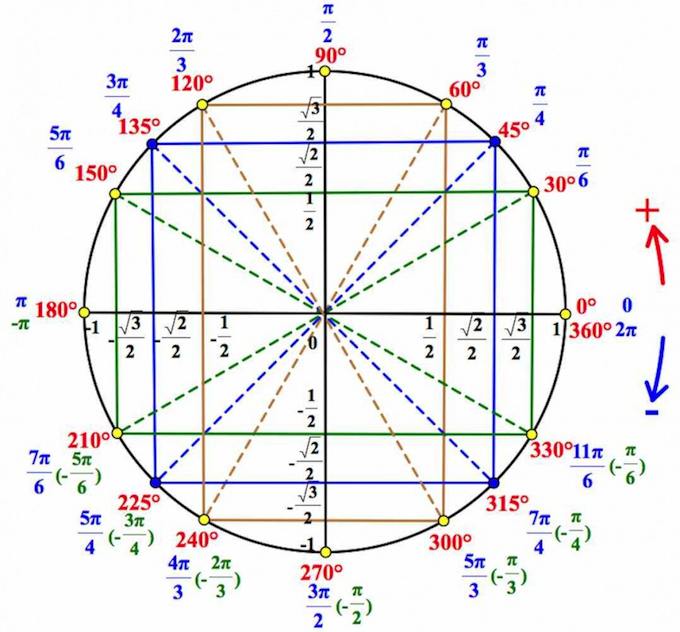
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг :

Мы же здесь будем все подробно разбирать шаг за шагом + показать

Тригонометрический круг – не роскошь, а необходимость

Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…

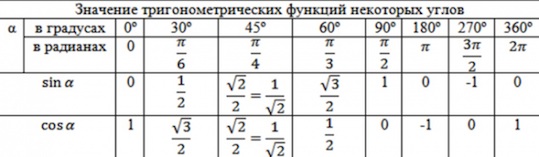
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.

Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!

Нас выручит тригонометрический круг ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!

К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, градусов, или .

Никак. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!

А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.

Знакомство с тригонометрическим кругом

Давайте по порядку.

Сначала выпишем вот такой ряд чисел:

И, наконец, такой:

Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .

Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».

И зачем оно нам?

Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.

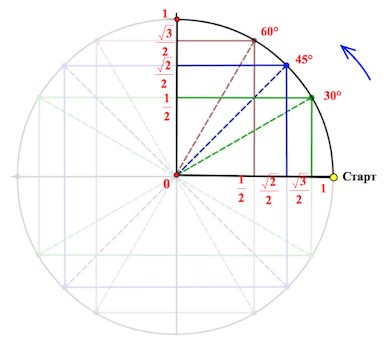
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).

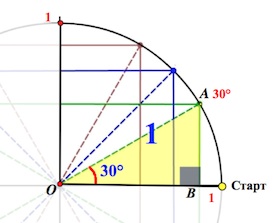
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .

Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.

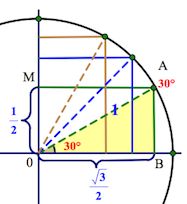
Это почему же, спросите вы?

Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.

Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть ).

Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора

Надеюсь, уже что-то становится понятно?

Так вот точка В и будет соответствовать значению , а точка М – значению

Аналогично с остальными значениями первой четверти.

Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . Про тангенс и котангенс позже.

Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.

Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг , без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.

Видео:Как искать точки на тригонометрической окружности.Скачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

Видео:ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬСкачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,