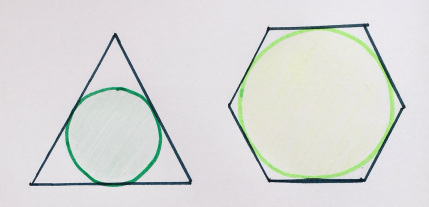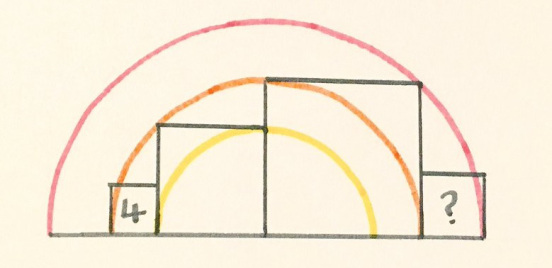Три окружности в квадрате

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:ПЛОЩАДЬ КРУГА. ЛАЙФХАК #math #логика #загадка #математика #геометрияСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Окружность, вписанная в квадрат

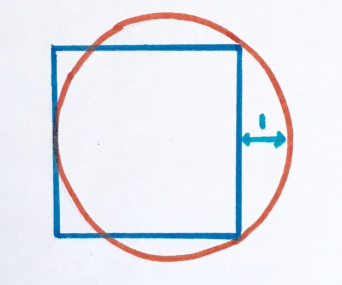
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:Три окружности в прямоугольнике.Скачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Площадь круга. Математика 6 класс.Скачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Радиус и диаметрСкачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Метод выделения полного квадрата. 8 класс.Скачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

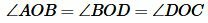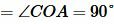(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

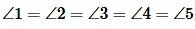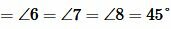(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Двадцать задачек (по безумной, восхитительной геометрии)

Предупреждение врача. Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.

Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.

Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).

Наслаждайтесь. И не говорите, что врач не предупреждал.

Видео:Длина окружности. Математика 6 класс.Скачать

1. Сад часов

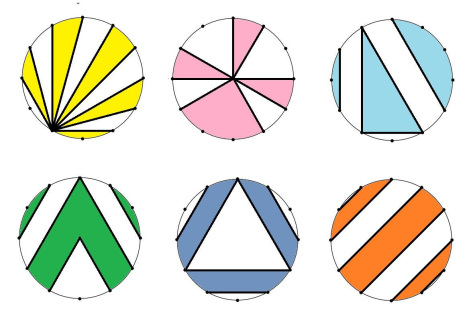
Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)

«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».

Видео:Лучший способ найти площадь кругаСкачать

2. Опрокинутый квадрат

(Как по мне, это классика).

Видео:✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

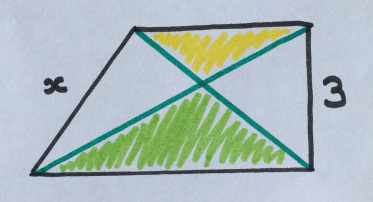
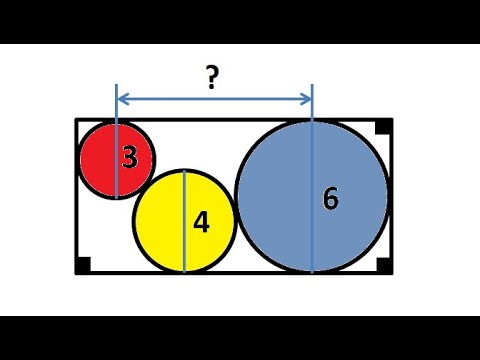
3. Это ловушка

В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?

«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».

Видео:Что важнее площадь или периметр?Скачать

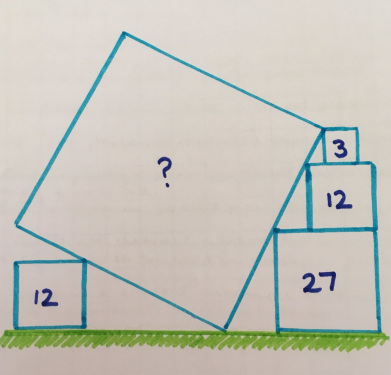
4. Три квадратных тарелки

Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?

«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

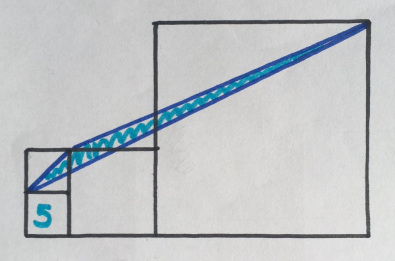
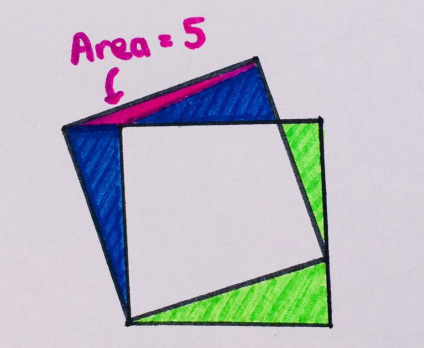
5. Красивая стрижка

Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?

«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».

Видео:Площадь квадрата. Как найти площадь квадрата?Скачать

6. Все люди рождены равными

«Ещё одна переделка, которую я предпочитаю оригиналу».

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

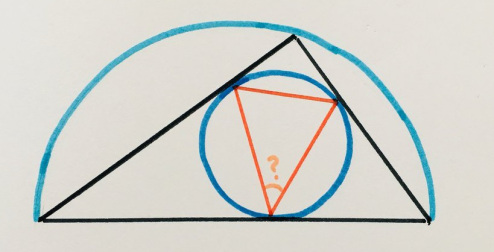
7. Полукруг турдакен

«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

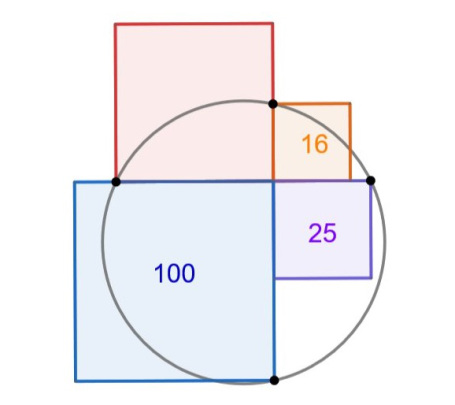
8. Степенные хорды

Какова площадь круга?

«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»

Видео:Задача, которую боятсяСкачать

9. Сказка о двух кругах

У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.

«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»

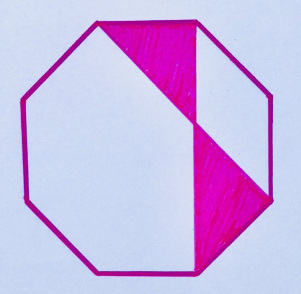
10. Doc Oct

У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?

«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».

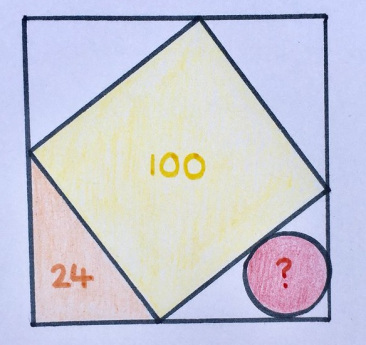
11. Всё в квадрате

«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».

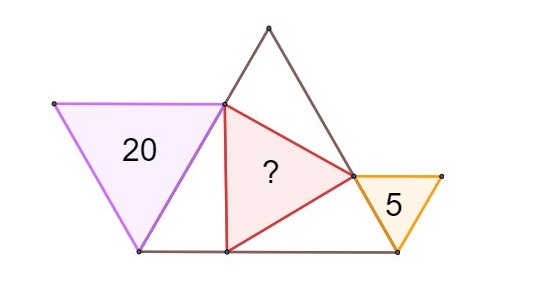
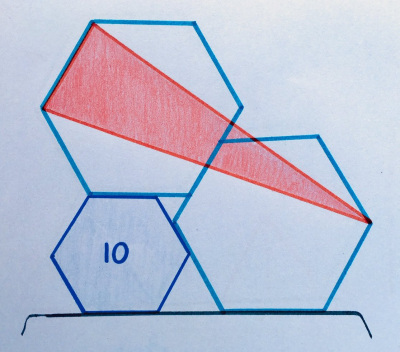
12. Шип в улье

Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?

«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».

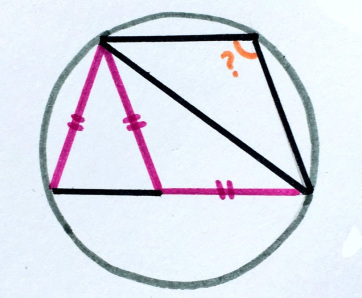
13. Я видел равнобедренных

Все четыре треугольника равнобедренные. Найдите угол.

«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»

14. Зеленый против синего

На картинке больше зелёного цвета или синего (и на сколько)?

«Ещё одна из моих любимых».

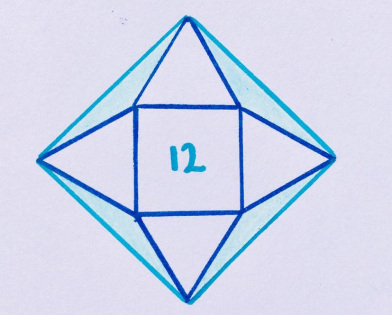
15. Резцы по камню

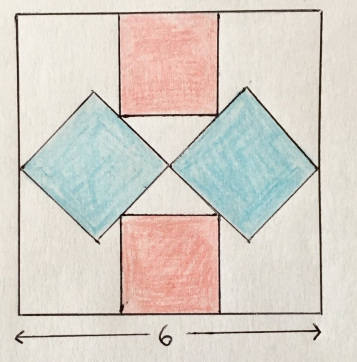
Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?

«Тут самое лучшее — действительно хорошие решения по рассечению площади».

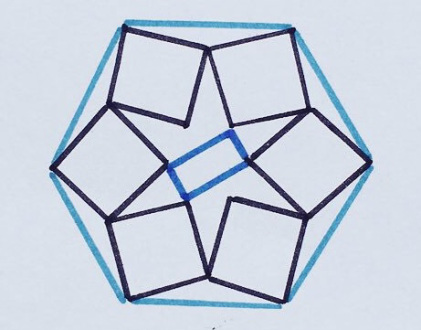
16. Едем, едем, уехалиугольник

Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?

«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»

17. Только один факт

Какова площадь этого квадрата?

«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».

18. Стиральная машина

Какая часть большого квадрата закрашена?

«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».

19. Летающие флаги

У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?

«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».

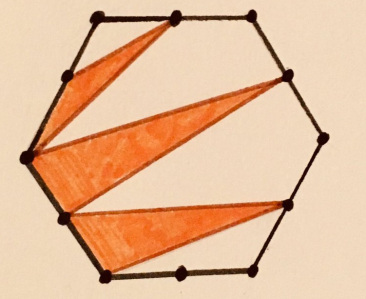
20. Тигрогон

Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.

«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».

БОНУС:

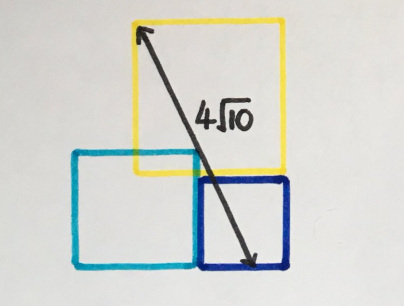
Закат над Квадратным городом

У левого квадрата площадь 4. Какова площадь правого квадрата?

«Мне нравится эта задачка, она напоминает закат над городом скверов.”

Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.

Как вы пришли к разработке своих головоломок?

Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.

Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.

Как проходит творческий процесс?

Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.

Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?

Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.

Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.

Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.

Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?

Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!

Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!

Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.

Советы для потенциальных создателей головоломок?

Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.

Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:

1. Красивая постановка задачи. Предоставьте минимум информации, чтобы читателю стало интересно, как вообще можно решить такую задачу. Или несколько дразнящих кусочков информации, каждый из которых якобы предлагает способ решения. Правильные многоугольники и круги — фантастические штуки, потому что скрывают огромное количество информации.
2. Красивый метод. Трюк или кратчайший путь, или внезапное озарение, которое всё упрощает. Это может быть не самый очевидный метод. Я видела много задачек, которые решаются с помощью алгебры или иррациональных чисел, или ужасных выражений с pi, а в конце всё внезапно сокращается — и я понимаю, что есть более простой способ.
3. Красивый ответ. Мало удовольствия работать над головоломкой, чтобы в конце получить некрасивый ответ.

В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы. Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.

math4school.ru

Сангаку. Священная математика

Период Эдо

Первый осенний дождь.
И обезьяна хочет
Маленький соломенный плащ.

Период Эдо (1603–1867) – это период истории Японии начавшийся с приходом к власти сёгуната Токугава и проведением им политики сакуку : закрытием всех государственных границ, прекращение всех возможных торговых и культурных связей с внешним миром, период полной изоляции Японии. Однако именно эта полная культурная изоляция привела к бурному расцвету во многих областях культуры японского народа. Именно в этом периоде появляются ярчайшие представители японской культуры: в литературе – Мацуо Басё (1644 – 1694), в живописи – Кацусика Хокусай (1760 – 1849), в математике – Секи Кова (1642 – 1708).

Кацусика Хокусай. Ирисы и луговая цикада. Гравюра, около 1832 года

Период изоляции привёл также к созданию уникальной японской математической школы – васан (в отличие от западной – иосан ). Васан – независимый вид математики, а точнее, математических традиций, распространенный и успешно развивавшийся в Японии в период Эдо. Ряд математических достижений японскими математиками были осуществлены в одно и то же время со своими европейскими коллегами, а некоторые даже раньше. Однако, с наступлением эпохи Мэйдзи (1868 – 1912) границы Японии вновь открылись для западного влияния и учеными была позаимствована европейская математическая традиция, нивелировавшая значимость оригинальных методов, созданных в рамках васан.

Секи Такакадзу (ок. 1642 – 1708)

Уровень васан испытал резкий скачок в конце XVII века, в основном – благодаря работам Секи Такакадзу (известного так же как Секи Кова или Сэки Кова), самого известного математика Японии. О силе Секи рассказывается множество историй, однако, как и к историям про юного Гаусса, к ним стоит относиться с долей скептицизма. Большинство работ Секи было опубликовано посмертно его учениками, и поскольку математики в Японии традиционно проявляли уважение к своим учителям, всегда трудно в точности узнать, что сделал он, а что – не он. Точные дата и место рождения Секи неизвестны, но он был современником Ньютона и Лейбница.

Происходя из самураев, он был в детстве принят в благородную семью Секи Городзаэмона, и далее действовал под этой фамилией. Впоследствии он работал с казной клана Кофу, главой которого был лорд Токугава Цунасигэ. В 1704 году Секи был взят на работу, как самурай сёгуната, в правительство Токугава, и работал два года казначеем среднего уровня. В 1706 году он вышел в отставку, а в 1708 – умер.

Секи возмужал в подходящий момент, как раз в эру Гэнроку, и у него была возможность изучить обильное количество математических книг, которые тогда издавались. В 1672 году, когда ему было около 30 лет, он написал свою первую рукопись. Из книг Секи при его жизни была опубликована лишь одна. Умирая, он оставил 21 книгу в рукописях, включая 7 по астрономии. В 1712 году его ученик Араки Мурахидэ опубликовал 4 тома работ Секи под заглавием «Коллекция важных математических результатов». Именно из этой коллекции и известно о многих достижениях Секи.

Хотя иногда и появляются сомнения в ассоциации имени Секи с изобретением энри (определённого интеграла), несомненно, что именно он первым разработал теорию определителей, за десятилетие до Лейбница. С помощью своего собственного способа вписывания правильных многоугольников в окружность получил значение π = 3,14159265359 , правильно вычислив 11 его значащих цифр. Он, также, открыл числа Бернулли до Якоба Бернулли, и схему Горнера за 150 лет до того как эта процедура стала известна на Западе, после того, как английский школьный учитель Уильям Горнер (1786 – 1837) опубликовал её в 1830-м году.

Оригинальные обозначения Секи для определителей Один из подлинных чертежей Секи для 15-угольника
из его рукописи 1633 года «Кайфуку дай» из его книги «Кацуё: санпо»

Увы, Япония в эпоху Эдо сохраняла средневековый, к тому же изолированный от внешнего мира, жизненный уклад. Возможно, именно поэтому достижения Секи Ковы не получили дальнейшего развития, и японские математики стали вновь показывать результаты мирового уровня только в 20 веке, включившись в общемировой научный процесс.

Приношения богам

Надо заметить, что математика XVII века и в Японии, и в Европе была весьма своеобразным интеллектуальным занятием, сохранившим в себе нечто от цеховых традиций средневековья. Обычной была ситуация, когда отдельные мастера, придумав какую-нибудь сложную задачу, бросали публичный вызов своим собратьям по цеху, предлагая им найти решение и показать своё мастерство. Методы решения задач держались в тайне от соперников, – точно так же, как любой цеховой мастер оберегал тайны своего профессионального мастерства. Пьер Ферма унёс с собой многие тайны своего искусства; и многочисленные открытия Ньютона ждали своей публикации не один десяток лет.

Однако к концу XVII века занятия математическими науками в Европе стали приобретать принципиально иную форму. «Вызовы на задачу» сменились публикациями в научных журналах. Теперь учёный, развивший новый метод, не хранил его в секрете как своё «тайное оружие», но сразу же раскрывал свои результаты перед коллегами в статье, утверждавшей его приоритет. Так европейская математика из интеллектуального досуга одарённых любителей науки стала постепенно превращаться в фабрику по систематическому и целенаправленному производству новых знаний, и на смену учёным-любителям пришли профессионалы, группировавшиеся в XVIII веке вокруг нескольких крупных академий, а в XIX веке – вокруг многочисленных университетов.

Однако в Японии переход к новым формам организации научной жизни в это же самое время не произошёл. Тогда как страны Запада активно шли вперёд по новому пути развития, самурайская Япония в эпоху Эдо изолировалась от западного мира, сохраняя средневековый жизненный уклад. Обычной была ситуация, когда отдельные мастера, придумав какую-нибудь сложную задачу, бросали публичный вызов своим собратьям по цеху, предлагая им найти решение и показать своё мастерство. Рисунки к этим задачам, а это как правило были геометрические задачи, красиво раскрашивались на деревянных досках и вывешивались в синтоистских храмах как дар богам ками .

Сангаку (1893), префектура Фукусима Сангаку (1846), префектура Мияги

Японцы считают, что безымянных синтоистских божеств ками – восемь миллионов, и все они тайно странствуют по земле. Когда человеку открывается что-то прекрасное, это означает, что рядом с ним прошло незримое божество. Как пишут в предисловии к своей книге собиратели и исследователи задач японской храмовой геометрии Х. Фукагава и Д. Педое

чувство формы и восприятие природной красоты всегда отличали жителей Японии, так что не удивительно, что геометрия, притягательная своей красотой и неочевидностью задач и теорем, стала для практикующих это искусство людей не только развлечением, но и подходящим предметом для приношений богам.

Сангаку

Чертежи к теоремам вырезались на деревянных досках и красиво раскрашивались. Такие деревянные таблички получили название сангаку (или сан гаку , буквальный перевод: счётная или математическая дощечка).

Не все доски посвящены геометрическим задачам: на некоторых решались диофантовы уравнения или отыскивались объёмы криволинейных тел. На большинстве досок приводился только результат, а доказательство отсутствовало. Готовые доски вывешивались над входом в синтоистское святилище или буддистский храм в качестве приношения богам, а заодно – и вызова коллегам.

Структура сангаку почти всегда одинакова. После посвящения, справа налево следуют один за другим раскрашенные чертежи, под каждым из них условие задачи и ответ. Задачи предполагались вызовом: «Попробуй реши» – для своих учеников или коллег. Каждая табличка содержит от одной до 16 – 18 задач разной степени трудности, иногда, весьма трудных.

Задачи васан можно было найти не только в храмах. В эпоху Эдо 12 сборников задач сангаку было издано в печати, и сотни других задач остались в неопубликованных рукописях. Более того, авторы, вывешивавшие новые сангаку, безжалостно убирали задачи из более ранних коллекций. Ни об этих табличках, ни о книгах не следует думать, как о текстах в современном смысле; они никоим образом не составляют связного изложения васан. На отдельной сангаку задача, доступная 12-летнему ребёнку, может соседствовать с задачей, которая поставит в тупик выпускника университета. Частично, причина этого в том, что сангаку часто создавались группами людей с разными уровнями подготовки.

Круг основных идей японской храмовой геометрии довольно разнообразен и немного непривычен для геометра, воспитанного на традициях, теоремах и картинках западной геометрической школы, преимущественно унаследованной от древних греков. Первое бросающееся в глаза отличие – это повышенное внимание японских геометров к окружностям и эллипсам: как правило, ни одна табличка сангаку не обходится без задач об окружностях. Более того, количество окружностей в одной задаче может быть довольно велико, а иногда подразумеваться и бесконечным.

Хотя техника работы с окружностями не выходит за круг метрических теорем, не устаёшь удивляться наблюдательности и изощрённости создателей сангаку. В отличие от западной математики, в васан нет теорем о пересечении нескольких прямых в одной точке и не фигурируют другие коники, кроме эллипса. Возможно, это связано с тем, что в Японии эллипс мыслился не как сечение конуса, что привычно для западной геометрии, но как сечение цилиндра.

Многие из теорем сангаку по своим темам и стилю заметно отличаются от теорем, известных в геометрии Запада, а некоторые из них повторяют достижения европейской математики Нового времени. Японскими геометрами были открыты и доказаны многочисленные теоремы о цепях Штейнера, которые в европейской геометрии доказывались с помощью метода инверсии. Характерным было также использование пространственных образов при доказательстве планиметрических теорем. В частности, возможно, что в качестве аналога метода инверсии японские математики использовали стереографическую проекцию.

Вообще же метод открытия геометрических теорем, практиковавшийся японскими геометрами, основывался на интенсивной и продолжительной концентрации на рассматриваемом чертеже. Когда одного геометра спросили, как он получил свои замечательные теоремы об эллипсах, он ответил, что не размышлял ни над чем, кроме эллипсов, в течение последних десяти лет! Интересно, что когда японские геометры получили в свои руки китайский перевод «Начал» Евклида, они были очень сильно удивлены. «Зачем, – сказали они, – доказывать такие очевидные факты, когда есть ещё столько красивых и сложных геометрических теорем?»

Среди задач сангаку изредка встречаются арифметические задачи. Предполагалось решение этих задач с помощью соробана – японских счёт.

Соробан – японские счёты (абак). В дословном переводе с японского языка – «счётная доска».
Происходит от китайского суаньпаня, завезённого в Японию в Средние века.

Интересно, что соробан сегодня переживает настоящее возрождение: не только по всей Японии, но и во всём мире открываются школы по обучению счёта на соробане. Соробан введён как общеобязательный предмет в младших классах японских школ наряду с чтением, письмом и каллиграфией. Соробан является самым быстрым в мире механическим счётным устройством и неотъемлемой частью японской культуры.

Следующая табличка посвящена единственной арифметической задаче:

На этой табличке изображён соробан с отложенным на его костяшках 47-значным числом

Задача состоит в вычислении на соробане корня 16 степени из этого числа. Ответ: 753. Поистине фантастически виртуозная техника вычислений!

В сангаку 1807 года приводится алгебраическая задача решения системы уравнений в целых числах

7 √ x + 7 √ y + 7 √ z = 12.

В табличке приведено решение

x = 5 7 = 78125, y = 4 7 = 16384, z = 3 7 = 2187.

Кроме того, поставлена задача найти все решения этой системы при произвольных правых частях уравнений. Система сводится к уравнению 49-ой степени. Непростой задачей является уже получение этого уравнения.

В середине XVIII века население Эдо – будущего Токио – достигало 1 000 000 человек. Население Киото и Осаки составляло примерно по 400 000 человек. Наибольшее число дошедших до наших дней сангаку равно 880. Некоторые из задач еле заметны. Тот, кто не знает их достаточно хорошо, может ошибиться, глядя на плоскую деревянную дощечку. Число всех сангаку, созданных в период изоляции, составляет примерно 5000. Получается, что в среднем за 250 лет сакоку создавалось примерно 20 сангаку в год.

В течение более двух веков японские математики – профессионалы и любители, мужчины и женщины – создавали то, что по сути было такими покрытыми математикой витражами: деревянные таблички, украшенные прекрасными геометрическими задачами, являвшиеся одновременно и произведениями искусства, и религиозными дарами. Создатели сангаку вывешивали их десятками и сотнями в буддистских храмах и синтоистских святилищах по всей Японии, и по этой причине всё собрание задач сангаку стало известно, как храмовая геометрия, священная математика .

Рассмотрим далее несколько задач, взятых из сангаку.

Восемь окружностей

Шесть из восьми кругов имеют очевидные отношения между их радиусами. В порядке уменьшения длин радиусов:

Необходимо найти радиус двух маленьких окружностей по радиусу самой большой.

Будем полагать, радиус самой большой окружности равным R = 3 r . Тогда r – радиус каждой окружности в вертикальном триплете и 2r – радиус каждого из двух больших двойников. Пусть х – неизвестный радиус.

По теореме Пифагора:

AB 2 = OB 2 + ОA 2 ,

Так как R = 3r , то радиус наименьшей окружности выражается через радиус наибольшей окружности следующим образом:

Квадрат и окружность в готическом куполе

Две четверти окружности, вписанные в квадрат, образуют фигуру, похожую на готический купол. В этот готический купол вписан квадрат и окружность, как показано на рисунке. Как относятся радиус этой окружности и сторона этого квадрата?

Будем полагать, что сторона большего квадрата равна 1 , сторона меньшего квадрата GF = х и радиус окружности с центром в точке О равен r .

По теореме Пифагора из прямоугольного Δ AFG имеем:

AG 2 = AF 2 + FG 2 ,

Единственный положительный корень последнего квадратного уравнения х = 3 /₅ .

Применим теорему Пифагора к Δ AMO и получим:

AO 2 = AM 2 + MO 2 ,

Последнее уравнение сводится к линейному уравнению с корнем r = 39 /₃₂₀ .

Три касающиеся окружности

Три окружности с центрами А, В, С и радиусами a, b, c, соответственно, касаются друг друга и прямой l и расположены так, как показано на рисунке. Докажите, что

Возможно, это одна из наиболее известных задач среди тех, которые встречаются в сангаку. Редкая книга или статья о японской храмовой геометрии обходится без упоминания об этих трёх окружностях и прямой, попарно касающихся друг друга. Рассматриваемый результат, конечно, был известен ещё древним грекам, что никак не умаляет достижений японских математиков. Навряд ли мы узнаем, как к решению этой задачи подходили в период Эдо в Японии. Мы же выбрали технически простой способ доказательства – используются лишь теорема Пифагора и простейшие алгебраические преобразования, – но по-своему элегантный и тонкий. Ниже приведено изображение сангаку с этой жемчужиной васан:

Сангаку с задачей о трёх касающихся окружностях и прямой.
Префектура Гумма, 1824 год

Как видим на следующем рисунке, мы имеем дело с тремя прямоугольными треугольниками, гипотенузами которых служат отрезки попарно соединяющие центры данных окружностей.

Введём вспомогательные отрезки x и y , как показано на рисунке. Рассматривая треугольники сверху вниз и слева направо выпишем тройки их сторон:

Тогда из теоремы Пифагора следует справедливость системы: