Три окружности радиуса 6 касаются друг друга

В 17:17 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Видео:Геометрия Три окружности радиусов R1 = 6 см, R2 = 7 см, R3 = 8 см попарно касаются друг другаСкачать

Вопрос вызвавший трудности

Видео:Три окружности касаются прямой и друг друга внешним образомСкачать

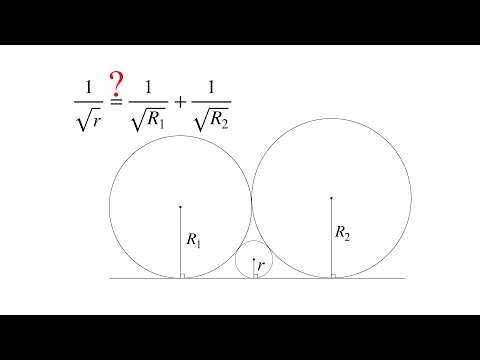
Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Три окружности, радиусы которых равны 6 см, 2 см и 1 см, попарно касаются друг друга внешним образом. Найдите площадь треугольника, вершинами которого являются центры этих окружностей

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

решение задания по геометрии

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Матвеева Оксана Анатольевна — автор студенческих работ, заработанная сумма за прошлый месяц 91 600 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

Видео:Геометрия Три окружности разных радиусов попарно касаются друг друга. Отрезки, соединяющие их центрыСкачать

Три окружности, радиусы которых равны 6 см, 2 см и 1 см, попарно касаются друг друга внешним образом. Найдите площадь треугольника,

В 17:17 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Видео:Три окружностиСкачать

Вопрос вызвавший трудности

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Три окружности, радиусы которых равны 6 см, 2 см и 1 см, попарно касаются друг друга внешним образом. Найдите площадь треугольника, вершинами которого являются центры этих окружностей

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

решение задания по геометрии

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Матвеева Оксана Анатольевна — автор студенческих работ, заработанная сумма за прошлый месяц 91 600 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

Видео:ЕГЭ Задание 16 Комбинация трёх окружностейСкачать

Три окружности радиуса 6 касаются друг друга

1. Правильно сделать рисунок. К сожалению не проходят вложения.

Из центров окружностей — первых двух и четвертой — образуется равнобедренный тр-ик О1О2О3 с основанием О1О2= 12 и боковой стороной:

О1О3=О2О3 = 6+х, где х — искомый радиус 4-ой окр-ти.

Высота этого тр-ка О3А = 12-х и с другой стороны по теореме Пифагора:

Итак получим уравнение:

Ответ: 4 см.

2. АС = 6, АВ = ВС = 5. АN,BD,CM — высоты

AО= CО = AD/cosa, где а = угол МСА = уголNAC = угол ABD

cosa = BD/АВ = (кор(25-9))/5 = 4/5

Тогда: АО = СО = 3/(4/5) = 15/4

OD = AD*tga = 3*3/4 = 9/4

BO = BD — OD = 4 — (9/4) = 7/4

Ответ: 15/4; 15/4; 7/4.

3.Центр впис. окр. — на пересечении биссектрис углов тр-ка АВС.

r — радиус вписаной окр-ти.

Из чертежа (надо правильно его выполнить, проведя радиусы в точки касания): отрезки до точек касания равны r/tg(A/2), r/tg(B/2), r/(tg(c/2).

Тангенс половинного угла считается по формуле tg(a/2) = sina/(1+cosa).

Итак в нашей задаче надо найти r и тригоном. ф-ии углов тр-ка.

r=? S = pr и S = кор(p(p-a)(p-b)(p-c)), p = (6+9+12)/2 = 27/2

S = (27кор15)/4 r = S/p =(кор15)/2

Функции углов:cosB = (81+36-144)/(2*9*6) = — (1/4), sinB = (кор15)/4

По теореме синусов: 9/sinC = 12/sinB, sinC = (3кор15)/16, cosC = 11/16.

Аналогично: sinA = (кор15)/8, cosA = 7/8.

tg(A/2) = (кор15)/15; tg(B/2) = (кор15)/3; tg(C/2) = (кор15)/9.

Искомые отрезки равны: 15/2, 9/2, 3/2.

Попарно по сторонам:

Ответ:15/2 и 9/2; 9/2 и 3/2; 15/2 и 3/2.

📹 Видео

✓ Три окружности | Планиметрия | Олимпиада Ломоносов-2020 | Борис ТрушинСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

ЕГЭ Задание 16 Три окружностиСкачать

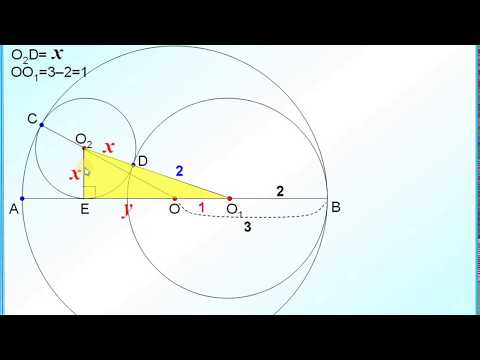
С4, егэ. Задача про три касающиеся друг друга окружностиСкачать

Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

ЕГЭ Задание 16 Внешнее касание трёх окружностейСкачать

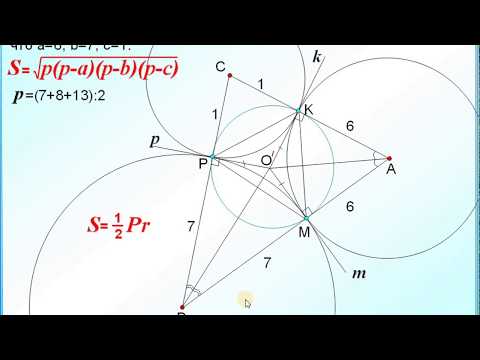
Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Задача по геометрии.Скачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать

Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать

Задача по геометрии.Скачать

КРАСИВАЯ ПЛАНИМЕТРИЧЕСКАЯ ЗАДАЧА (3 ОКРУЖНОСТИ)Скачать

Вирусная задаче из социальных сетей, которую почти никто не смог решитьСкачать