Треугольники в ромбе равны

В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Определение ромба

Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).

Примечание: квадрат является частным случаем ромба.

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Свойства ромба

Свойство 1

Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.

Свойство 2

Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.

Свойство 3

Диагонали ромба являются биссектрисами его углов.

Свойство 4

Сторону ромба a можно найти через его диагонали d₁ и d₂ (согласно теореме Пифагора).

• a – гипотенуза любого из 4 прямоугольных треугольников (например, ΔBEC );
• половины диагоналей d₁ и d₂ – катеты треугольников.

Свойство 5

В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Радиус вписанной в ромб окружности r вычисляется по формуле:

Видео:№540. Периметр треугольника CDE равен 55 см. В этот треугольник вписан ромб DMFN так, чтоСкачать

Признаки ромба

Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:

1. Его диагонали пересекаются под прямым углом.
2. Если его диагонали являются биссектрисами его углов.
3. Две смежные стороны равны (следовательно, все стороны равны).

Примечание: Любой четырехугольник, стороны которого равны, является ромбом.

Видео:Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать

Свойства ромба

Свойства ромба — это свойства параллелограмма плюс собственные свойства.

Свойства ромба

1) Стороны ромба равны (по определению ромба).

2) Противолежащие углы ромба равны (по свойству параллелограмма).

3) Сумма углов, прилежащих к одной стороне ромба, равна 180º (по свойству параллелограмма).

4) Диагонали ромба пересекаются и точкой пересечения делятся пополам (по свойству параллелограмма).

6) Диагонали ромба являются биссектрисами его углов.

7) Сумма квадратов диагоналей ромба равна сумме квадратов его сторон (по свойству параллелограмма).

8) Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба (по свойству параллелограмма).

9) Угол между высотами ромба, проведенными из вершины острого угла, равен тупому углу ромба.

Проиллюстрируем эти свойства для ромба ABCD:

3) ∠A+∠B=180º; ∠B+∠C=180º; ∠C+∠D=180º; ∠A+∠D=180º;

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Треугольники в ромбе равны

С помощю этого онлайн калькулятора ромба можно найти неизвестные этлементы ромба по известным элементам. Для нахождения неизвестных элементов ромба, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Видео:8 класс, 8 урок, Ромб и квадратСкачать

Определение ромба

Определение 1. Ромб − это параллелограмм, у которого все стороны равны.

На рисунке 1 изображен ромб ABCD.

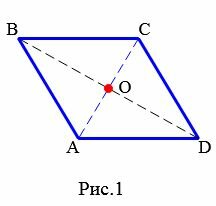Определение 2. Ромб − это четырехугольник, у которого все стороны равны.

Ромб разделяет плоскость на две части, одна из которых называется внутренней областью ромба, а другая внешней областью ромба.

Объединение ромба и ограниченной им части плоскости также называют ромбом.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Свойства ромба

Поскольку ромб является параллелограммом, то имеет следующие свойства:

• 1. У ромба противолежащие углы равны (( small angle A = angle C, ; angle B = angle D.) )
• 2. У ромба противолежащие стороны равны (( small AB = DC, ; BC=AD.) )
• 3. У ромба противолежащие стороны параллельны ( small( AB || DC, ; BC || AD).)
• 4. У ромба соседние углы дополняют друг друга до 180° ( small ( angle A +angle B=180°, ) ( small angle C + angle D=180°).)
• 5. Диагонали ромба точкой пересечения делятся пополам ( small ( AO = OC, ) ( small BO=OD).)

Ромб имеет также и следующие свойства:

• 6. Диагонали ромба пересекаются под прямым углом (( small AC perp BD.) )
• 7. Диагонали ромба являются биссектрисами его углов (( small angle ABD = angle CBD, ) ( small angle ADB = angle CDB, ) ( small angle DAC = angle BAC, ) ( small angle BCA = angle DCA. ))
• 8. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
• 9. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженная на четыре ( small (AC^2+BD^2=4AB^2). )

Докажем свойства 6 и 7, сформулировав следующую теорему:

Теорема 1. Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Доказательство. По определению 1, ( small AD = DC ) (Рис.2). Следовательно треугольник ( small DAC ) равнобедренный. Тогда ( small angle DCO = angle DAO. ) Учитывая, что ( small AO = OC ) (свойство 5 ромба), получим, что треугольники ( small DOA ) и ( small DOC ) равны по двум сторонам и углу между ними (см. статью Треугольники. Признаки равенства треугольников). Тогда равны углы DOC и DOA. Но эти углы смежные и их сумма равна 180°. Следовательно ( small angle DOC= angle DOA=90°. ) То есть диагонали AC и BD перпендикулярны.

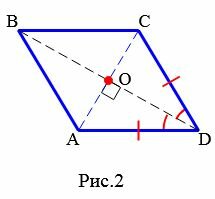Из равенства треугольников ( small DOA ) и ( small DOC ) также следует, что ( small angle CDO= angle ADO,) следовательно BD является биссектрисой угла ADС, то есть BD является биссектрисой ромба ABCD.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Признаки ромба

Признак 1. Если смежные стороны параллелограмма равны, то этот параллелограмм − ромб.

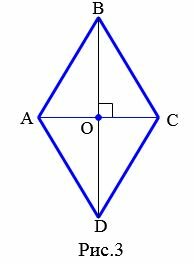Доказательство. Пусть смежные стороны параллелограмма ABCD равны. То есть имеем: AB=BC (Рис.3). У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда DC=AB=BC=AD. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм − ромб.

Доказательство. Пусть диагонали параллелограмма ABCD перпендикулярны (Рис.3). Рассмотрим прямоугольные треугольники AOB и COB. Так как у параллелограмма диагонали точкой пересечения разделяются пополам (Свойство 2 статьи Параллелограмм), то AO=OC. Тогда прямоугольные треугольники AOB и COB равны по двум катетам (AO=OC, BO общий катет (см. статью Прямоугольный треугольник. Свойства, признаки равенства)). Следовательно AB=BC. Тогда по признаку 1 этот параллелограмм является ромбом.

Признак 3. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм − ромб.

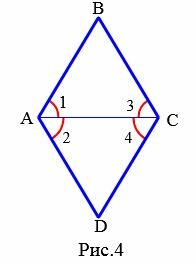Доказательство. Пусть диагональ AC параллелограмма ABCD является биссектрисой угла BAD (Рис.4). Тогда ( small angle 1= angle 2 .) У параллелограмма ABCD ( small AB || DC .) Тогда для параллельных прямых AB и DC и секущей AC справедливо равенство ( small angle 1= angle 4 .) (см теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично, для параллельных прямых BC и AD и секущей AC справедливо равенство ( small angle 2= angle 3 .) Так как ( small angle 1= angle 2 ,) то ( small angle 1= angle 2=angle 3= angle 4 .) Из ( small angle 1= angle 3) следует, что треугольник ABC равнобедренный (Признак 2 статьи Равнобедренный треугольник). Тогда AB=BC. У параллелограмма противоположные стороны равны (Свойство 1 статьи Параллелограмм). Тогда AB=BC=CD=DA. То есть все стороны параллелограмма равны и по определению 1, этот параллелограмм является ромбом.

Признак 4. Если стороны четырехугольника равны, то этот четырехугольник − ромб.

Доказательство. Пусть у четырехугольника все стороны равны. Тогда этот четырехугольник является параллелограммом (признак 2 статьи Параллелограмм). А по определению 1, этот параллелограмм является ромбом.

🔥 Видео

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Про параллелограмм, который ромбСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

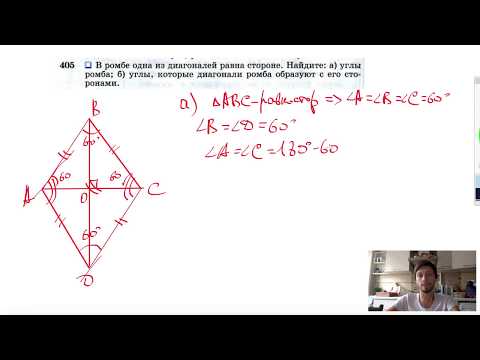
№405. В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы,Скачать

№476. Докажите, что площадь ромба равна половине произведения его диагоналей. ВычислитеСкачать

Прямоугольник. 8 класс.Скачать

Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.Скачать

Ромб и его свойства доказательствоСкачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Ромб. 8 класс.Скачать

№407. Найдите углы, которые образуют диагонали ромба с его сторонами, если одинСкачать