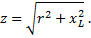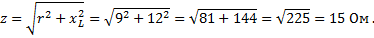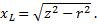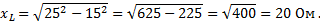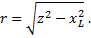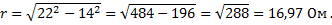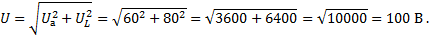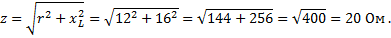Треугольник сопротивлений rl цепи

Автор: Евгений Живоглядов.
Дата публикации: 01 апреля 2015 .
Категория: Статьи.

Если стороны треугольника напряжений (рисунок 1, а) разделить на ток I (рисунок 1, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому – треугольник сопротивлений (рисунок 1, в).

Рисунок 1. Получение треугольника сопротивлений

В треугольнике сопротивления, показанном отдельно на рисунке 2, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного x_L сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

Если одно из сопротивлений цепи (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко можно убедиться непосредственным расчетом.

Пример 1. Определить полное сопротивление цепи, в которой r = 9 Ом и x_L = 12 Ом.

Было бы совершенно неправильно, если бы для определенного полного сопротивления были арифметически сложены оба сопротивления r и x_L, так как

Результат, как мы видим, в этом случае получается неверный.

Пример 2. Полное сопротивление обмотки электромагнита z = 25 Ом. Активное сопротивление обмотки r = 15 Ом. Определить индуктивное сопротивление.

Пример 3. Индуктивное сопротивление обмотки электродвигателя переменного тока равно 14 Ом. Полное сопротивление ее равно 22 Ом. Найти активное сопротивление.

Пример 4. В цепи, изображенной на рисунке 3, определить показание вольтметра.

Рисунок 3. К примеру 4

Определим общее сопротивление:

Если умножить z на ток I, получим:

то есть тот же результат, что и выше.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

Видео:Откуда взялась формула полного сопротивления цепи? Треугольник напряжений, треугольник сопротивленийСкачать

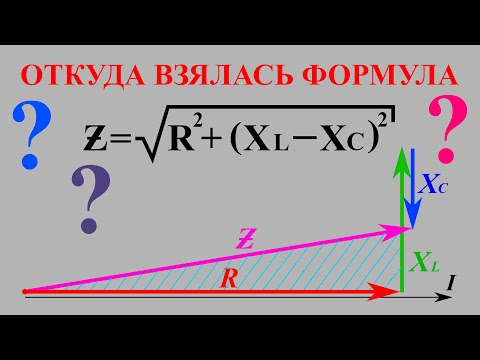
Последовательная RL-цепь

Рассмотрим цепь, состоящую из последовательно соединенных резистора R и катушки L, в электротехнике такая цепь часто называется последовательной RL-цепью.

Напряжение, приложенное к цепи равно

По второму Кирхгофа, для рассматриваемой цепи можно записать выражение

Напряжение на резисторе и катушке равно

Тогда напряжение, приложенное к цепи

Подставив ток в выражение для напряжения, получим

Из выше приведенной формулы первое слагаемое это напряжение на резисторе, то есть

Из этого можно сделать вывод, что ток и напряжение в резисторе совпадают по фазе.

Напряжение на катушке

Напряжение на катушке опережает ток на угол π/2.

Реактивное сопротивление катушки равно

Сопротивление катушки зависит от частоты. При постоянном токе, частота равна нулю, а значит и сопротивление тоже.

Сдвиг фаз RL-цепи можно определить по формуле

Полное сопротивление RL-цепи

Амплитудное значение тока

К цепи, состоящей из последовательно соединенных катушки и резистора приложено синусоидальное напряжение. Ток в цепи равен 1,2 А. Сопротивление резистора 10 Ом, индуктивность катушки 26 мГн. Найдите напряжение U, U_R, U_L, сдвиг фаз φ. Постройте векторную диаграмму.

Найдем напряжение на каждом из элементов, зная ток в цепи и их сопротивление

Найдем сдвиг фаз между током и напряжением в цепи. В нашем случае реактивное сопротивление x состоит только из индуктивного сопротивления x_L

Построим векторную диаграмму напряжений для нашей цепи. Подробнее об этом в статье Построение векторных диаграмм.

Напряжение в цепи найдем из треугольника напряжений

Видео:R, L, C в цепи переменного тока/Треугольник сопротивлений/Сдвиг по фазеСкачать

Анализ линейных электрических цепей (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

Сравнение реактивного (1.22) и комплексного (1.31) сопротивлений индуктивности показывает, что на комплексной плоскости реактивное (индуктивное) сопротивление катушки откладывают на положительной вертикальной полуоси (рис. 1.32, б), потому что эта величина мнимая и положительная.

Запишем выражения комплексных амплитуд тока и напряжения для цепи, содержащей емкость. Из (1.16) и (1.26) следует, что:

,

где UmC и Im, а также ju и ji связаны соотношениями (1.27). Векторы напряжения на емкости и тока в ней сдвинуты друг относительно друга на –90°, при этом ток опережает напряжение (рис. 1.31, в).

Комплексное сопротивление емкости найдем как:

Здесь учтено, что .

Очевидно, что реактивное сопротивление емкости является мнимым отрицательным числом, на комплексной плоскости оно откладывается на отрицательной вертикальной полуоси (рис. 1.32, в).

Мы уже знаем, что любое комплексное число, записанное в алгебраической форме , имеет вещественную а и мнимую jb составляющие, а число, записанное в показательной форме – модуль A и аргумент j.

Анализ выражений (1показывает, что комплексное сопротивление резистора является вещественным и не содержит мнимой составляющей, его аргумент равен нулю; комплексное сопротивление индуктивности, наоборот, является мнимым, его аргумент равен +90°; комплексное сопротивление емкости также мнимое, но аргумент его равен –90°.

На рис. 1.33, а и 1.34, а показаны последовательные RL и RC цепи. Комплексное сопротивление последовательной RL цепи в алгебраической форме содержит сумму положительного вещественного резистивного сопротивления R и положительного мнимого индуктивного сопротивления jXL (рис. 1.33, б):

где .

В показательной форме это сопротивление запишется в виде:

,

где модуль ZRL называется полным сопротивлением последовательной RL цепи, а аргумент jZ – углом этого сопротивления. Полное сопротивление ZRL и аргумент jZ подсчитываются, как это следует из рис. 1.33, б, по формулам

Пример 1.11. Определим комплексное сопротивление цепи, изображенной на рис. 1.33, а, на частоте 50 Гц для R = 10 Ом и L = 100 мГн.

Рассчитаем значение индуктивного сопротивления цепи, используя (1.31),

Комплексное сопротивление RL-цепи

В показательной форме комплексное сопротивление RL-цепи

Комплексное сопротивление последовательной RC цепи в алгебраической форме состоит из положительного вещественного резистивного сопротивления R и отрицательного мнимого емкостного (рис. 1.34, б):

где

В показательной форме это комплексное число выглядит как

,

где – полное сопротив­ление последовательной RC цепи;

– угол этого сопротивления.

Комплексное сопротивление ZRC изображено на рис. 1.34, б в виде вектора на комплексной плоскости. Там же показаны его проекции на вещественную и мнимую оси.

Прямоугольный треугольник, составленный из резистивного, реактивного и полного сопротивлений (рис. 1.35), называется треугольником сопротивлений.

Пример 1.12. Определим комплексное сопротивление цепи, изображенной на рис. 1.34, а, на частоте 5 кГц для R = 100 Ом, С = 318 нФ.

Рассчитаем значение емкостного сопротивления цепи

Комплексное сопротивление RC-цепи

Вектор комплексного сопротивления RC-цепи изображен на рис. 1.36.

Запишем комплексное сопротивление последовательной RLC цепи (рис. 1.37, а). Оно будет содержать положительное вещественное резистивное сопротивление R и мнимое сопротивление , знак которого будет зависеть от соотношения индуктивного XL и емкостного XC сопротивлений, следовательно:

,

где .

Напомним, что значения XL и XC зависят от частоты и от соответствующих элементов L и С, поэтому может случиться так, что на определенной частоте и при определенных значениях L и С значение XL будет больше значения XC, как это показано на рис. 1.37, б, или наоборот, значение XC будет больше, чем XL (рис. 1.37, в).

Из треугольника сопротивлений легко вычислить резистивное и реактивное сопротивления, зная полное сопротивление и его угол:

.

Случай, когда реактивное сопротивление Х = 0, т. е. XL = XC, является особым. Когда это имеет место, то говорят, что в последовательной RLC цепи возникает резонанс напряжений. Частота, на которой индуктивное и емкостное сопротивления оказываются равными, называется частотой резонанса напряжений. Комплексное сопротивление всей RLC цепи равно при этом резистивному сопротивлению R. В дальнейшем явление резонанса напряжений будет рассмотрено более детально.

Пример 1.13. Определим резистивное и реактивное сопротивления последовательной RLC цепи, комплексное сопротивление которой

Сопротивление X = XL – XC положительное, т. е. XL > XC, треугольник сопротивлений такой цепи изображен на рис. 1.38.

При параллельном соединении элементов удобнее иметь дело не с сопротивлениями, а с проводимостями – резистивной G = 1/R, реактивными и , полной Y = 1/Z и комплексной Y = 1/Z. Если при последовательном соединении элементов складыва
лись их комплексные сопротивления, то при параллельном соединении складываются их проводимости.

Для параллельной RLC цепи (рис. 1.39, а) ее комплексная проводимость запишется в виде:

,

где G = 1/R – резистивная проводимость;

– емкостная проводимость;

– индуктивная проводимость;

– реактивная проводимость;

– полная проводимость;

– угол проводимости.

Резистивную и реактивную проводимости можно найти из треугольника проводимостей (рис. 1.39, б):

.

Случай, когда реактивная проводимость В равна нулю, т. е. когда также представляет особый интерес. В этот момент в параллельной RLC цепи наступает резонанс токов. Поэтому частота, на которой происходит совпадение реактивных проводимостей ветвей получила название частоты резонанса токов. Комплексная проводимость всей цепи при резонансе становится равной резистивной проводимости G. Более подробно явление резонанса токов будет рассмотрено позднее.

Пример 1.14. Определить комплексное сопротивление параллельной RLC цепи (рис. 1.39, а) на частоте f = 1 кГц для R = 100 Ом, L = 10 мГн, С = 10 мкФ.

Элементы цепи соединены параллельно, поэтому рассчитаем вначале комплексную проводимость YRLC, используя выражение (1.36).

Комплексная проводимость цепи

Комплексное сопротивление цепи обратно пропорционально комплексной проводимости, поэтому

Из данного раздела мы узнали, что:

1.3. Расчет реакций цепи в символической
форме

Расчет реакций в цепи с одним источником. Используется следующий порядок расчета:

1. Цепь, содержащую источник гармонических колебаний, преобразуют, заменяя ее элементы их комплексными сопротивлениями, а мгновенные значения эдс, токов и напряжений записывая в комплексной (символической) форме.

2. Рассчитывают комплексные значения токов в ветвях и напряжений на сопротивлениях, используя закон Ома и законы Кирхгофа.

3. Определяют соответствующие мгновенные значения токов и напряжений в цепи.

Пример 1.15. Определим мгновенные значения тока и напряжений на элементах цепи, содержащей источник гармонического напряжения В, сопротивление R = 300 Ом, индуктивность L = 0,6 Гн и емкость С = = 0,625 мкФ (рис. 1.40).

В соответствии с порядком расчета реакции в цепи с одним источником заменяем элементы цепи их комплексными сопротивлениями.

Анализируя выражение для мгновенного значения напряжения u(t), определяем, что круговая частота w = 2000 рад/с, т. е. частота колебаний f = w/(2p) = = 318,3 Гц. Сопротивление R = 300 Ом остается неизменным. Индуктивность L = 0,6 Гн заменяется сопротивлением

Емкость С = 0,625 мкФ заменяется сопротивлением

Гармоническое напряжение пред­ставим в показательной форме записи в виде

В результате получаем схему, изображенную на рис. 1.41.

Для определения тока и напряжений в этой схеме рассчитаем вначале комплексное сопротивление цепи Z относительно зажимов источника. Все сопротивления включены последовательно, поэтому

Отметим, что индуктивное и емкостное сопротивления цепи частично компенсировали друг друга и что реактивное сопротивление цепи меньше по величине, чем сопротивление любого из реактивных элементов.

Фактически возможно полностью исключить наличие реактивного сопротивления в цепи, изменив частоту генератора напряжения до выполнения условия |ZL| = |ZC|.

В рассматриваемом примере сопротивление цепи имеет индуктивный характер, поскольку реактивная составляющая комплексного сопротивления цепи имеет знак «плюс».

Комплексный ток Im в цепи определим, используя закон Ома для комплексного напряжения Um­­ источника и комплексного сопротивления Z. Имеем:

Преобразуя комплексное сопротивление Z в показательную форму для упрощения деления комплексных чисел, получаем

Амплитудное значение тока равно 0,02 А, а начальная фаза равна –53°.

Напряжения на сопротивлениях цепи определяем, умножая ток Im на соответствующие сопротивления.

Ток Im имеет начальную фазу (–53°), напряжение UmR имеет такую же начальную фазу, т. е. векторы Im и UmR направлены по одной прямой на векторной диаграмме, изображенной на рис. 1.42.

Напряжение на индуктивности опережает ток на 90°, таким образом, UmL опережает вектор на горизонтальной оси рис. 1.42 на 37°.

Напряжение на емкости отстает от тока на 90°, а от горизонтальной оси на 143°.

Отметим также, что сдвиг фаз между UmL и UmС составляет 180°.

В соответствии с законом напряжений Кирхгофа

Последние два слагаемых представляют собой сум­му напряжений на индуктивности и емкости, и этот суммарный вектор может быть направлен либо по UmL, либо по UmС в зависимости от того, какое из этих напряжений больше по величине. В нашем случае он имеет направление UmL.

Вектор UmR может быть добавлен к сумме UmL + UmС и результатом является вектор Um, как показано на рис. 1.42.

Мгновенные значения тока и напряжений на элементах цепи можно записать в виде

Векторная диаграмма часто бывает полезна при объяснении и интерпретации результатов расчета.

Пример 1.16. Найдем токи и напряжения в цепи, изображенной на рис. 1.43, если заданы значения R1 = 2 Ом, R2 = 2 Ом, ХL = 4 Ом, ХС = 2 Ом, .

Во-первых, определим комплексное сопротивление Zаб параллельного соединения резистора R2 и емкостного сопротивления ХС:

Сопротивление Zаб можно представить в виде Zаб = = Rаб – jXаб.

Получаем эквивалентную схему, изображенную на рис. 1.44.

Эквивалентное комплексное сопротивление цепи определяется как

Ток (рис. 1.45) определяется по закону Ома:

Токи Im1 и Im2 определяем по формулам разброса:

Следует отметить, что согласно закону токов Кирхгофа, Im1 + Im2 = Im. Векторная диаграмма токов приведена на рис. 1.46.

Определим напряжения на элементах цепи (рис. 1.43):

Согласно закону напряжений Кирхгофа (рис. 1.47)

Расчет реакций в цепи с несколькими источниками. Все методы расчета цепей в режиме постоянного тока применимы и к расчету цепей при гармоническом воздействии. Методы наложения, узловых напряжений, контурных токов, эквивалентного генератора используются для определения реакций в цепи с несколькими источниками гармонических колебаний.

Расчет выполняется для символической формы записи токов, напряжений и сопротивлений цепи.

Пример 1.17. Методом наложения определим токи в ветвях цепи, изображенной на рис. 1.48, если заданы значения R1 = 2 Ом, ХL = 4 Ом, ХС = 2 Ом,

Выберем направления токов в ветвях цепи (рис. 1.48). Поскольку в схеме два источника, то истинные направления токов неизвестны, поэтому выбираем их произвольно.

Метод наложения основан на принципе суперпозиции, согласно которому реакция линейной цепи на сумму воздействий равна алгебраической сумме реакций от каждого воздействия в отдельности.

Частичные схемы, в каждой из которых оставлен только один источник, а другой заменен его внутренним сопротивлением, изображены на рис. 1.49, а и 1.49, б.

Рассчитаем токи в первой частичной схеме (рис. 1.49, а). Внутреннее сопротивление источника тока равно бесконечности, поэтому . По закону Ома

Рассмотрим вторую частичную схему (рис. 1.49, б). Ток равен току источника тока, т. е.

Токи и рассчитываем, используя формулу разброса,

Токи в ветвях исходной схемы

Пример 1.18. Методом узловых напряжений определим токи в ветвях цепи, изображенной на рис. 1.48.

Заземляем узел 2. Потенциал этого узла равен нулю, Vm2 = 0.

Для узла 1 составляем уравнение состояния:

В этом уравнении Y11 – это собственная проводимость 1 узла, т. е. сумма проводимостей всех ветвей, подсоединенных к узлу 1:

Y12 – взаимная проводимость узлов 1 и 2, совпадающая в рассматриваемом примере с величиной Y11;

Из уравнения состояния находим потенциал первого узла

Токи в ветвях находим по закону Ома:

Значения токов в ветвях цепи рис. 1.48 те же самые, что и при расчете методом наложения.

Пример 1.19. Методом контурных токов определим токи в ветвях цепи, изображенной на рис. 1.48.

Выберем направления обхода контуров в цепи (рис. 1.50).

Для определения контурного тока составляем урав­нение состояния:

В этом уравнении Z11 – собственное сопротивление 1 контура, равное сумме сопротивлений всех ветвей, образующих этот контур:

Z12 – взаимное сопротивление 1 и 2 контуров:

Из уравнения состояния находим контурный ток Imк1:

Зная контурные токи, находим токи ветвей,

Значения токов совпадают с теми, которые были получены при расчете цепи методами наложения и узловых напряжений.

Пример 1.20. Методом эквивалентного генератора определим ток Im1 в цепи, изображенной на рис. 1.48.

Разомкнем ветвь с емкостью и для определения напряжения холостого хода Umхх составим уравнение по второму закону Кирхгофа

В режиме холостого хода ток Imхх = –Imг, поэтому

Сопротивление эквивалентного генератора Zэг равно

Ток Im1 найдем по формуле

Получаем то же самое значение Im1, что и при применении других методов расчета.

Из данного раздела мы узнали, что

1.4. Комплексный коэффициент передачи

Рассмотрим электрическую цепь, изображенную на рис. 1.51.

Нас может интересовать любая реакция цепи (напряжение или ток в любом элементе или ветви цепи) на любое из приложенных воздействий. В этом случае цепь удобно представить четырехполюсником, на входе которого включен источник с заданным воздействием, а на выходе – интересующий нас элемент, например, как это сделано на рис. 1.52.

Символическое изображение напряжений и токов на входе и выходе четырехполюсника, показано на рис. 1.53.

Важнейшей характеристикой линейной электрической цепи является комплексный коэффициент передачи Н. Он определяется отношением комплексной амплитуды реакции к комплексной амплитуде воздействия.

В зависимости от того, что считается реакцией и воздействием, различают следующие виды коэффициентов передачи.

1. Комплексный коэффициент передачи по напряжению

2. Комплексный коэффициент передачи по току

3. Комплексное передаточное сопротивление

4. Комплексная передаточная проводимость

Комплексное число H может быть представлено в показательной форме

где Н – модуль передаточной функции, а j – ее аргумент.

Действительно, рассмотрим передаточную функцию

.

Модуль передаточной функции

представляет собой отношение амплитуды гармонической реакции цепи к амплитуде гармонического воздействия, т. е. показывает во сколько раз амплитуда гармонического колебания на входе цепи изменилась при прохождении колебания через цепь. Поэтому величину Hu называют коэффициентом передачи по напряжению.

Аргумент передаточной функции

показывает изменение начальной фазы входного колебания после передачи этого колебания по цепи и называется фазовым сдвигом.

Знание комплексного коэффициента передачи цепи позволяет вычислить реакцию цепи на гармоническое воздействие. Амплитуда реакции равна

а начальная ее фаза

Другими словами, чтобы найти амплитуду гармонического колебания на выходе цепи, нужно амплитуду входного гармонического колебания умножить на коэффициент передачи по напряжению, а чтобы найти начальную фазу выходного гармонического колебания, нужно к начальной фазе входного гармонического колебания добавить фазовый сдвиг, вносимый цепью.

В символической форме записи комплексная амплитуда гармонического колебания на выходе цепи определяется из соотношения:

Аналогичным образом вычисляют коэффициент передачи по току

и сдвиг фаз колебания тока

полное передаточное сопротивление цепи

и фазовый угол этого сопротивления

а также полную передаточную проводимость

и ее фазовый угол

В общем виде можно записать

Очевидно, что в схеме рис. 1.51 в качестве реакции может выступать напряжение или ток в любом элементе или любой ветви цепи, а в качестве воздействия использоваться не только напряжения или токи источников, но и любые напряжения или токи элементов (ветвей) цепи.

Пример 1.21. Найдем комплексный коэффициент передачи по напряжению цепи, приведенной в Примере 1.15, если реакцией цепи является напряжение на емкости uC(t).

При решении Примера 1.15 воздействие было записано в символической форме

Напряжение на емкости, т. е. реакция цепи, также было определено:

Комплексный коэффициент передачи

Коэффициент передачи по напряжению

показывает, что при прохождении по цепи амплитуда воздействия уменьшилась в 10 раз.

показывает, что напряжение на емкости отстает от входного колебания на 143°.

Пример 1.22. Найдем комплексный коэффициент передачи по току цепи, изображенной на рис. 1.54, если Imг = 5ej90°, А, R2 = 10 Ом, L = 30 мГн, f = 50 Гц, реакцией цепи является ток в индуктивности.

Для расчета комплексного коэффициента передачи по току

необходимо определить ток в индуктивности. Используя формулу разброса, получаем:

Комплексный коэффициент передачи по току

Очевидно, что комплексный коэффициент передачи цепи определяется значениями элементов цепи R2, L и частоты f.

Пример 1.23. Найдем напряжение на индуктивности uL(t) в цепи, приведенной в Примере 1.22, если комплексное передаточное сопротивление HZ = 6,86ej46,8° Ом.

Амплитуда напряжения на индуктивности

Начальная фаза напряжения на индуктивности

Мгновенное значение напряжения

Из данного раздела мы узнали, что

Вопросы и задания для самоконтроля

1. Какие колебания называются гармоническими?

2. Какие параметры характеризуют гармоническое колебание?

3. Как определяется величина и знак начальной фазы гармонического колебания по его графику?

4. Как связаны частота и период гармонического колебания?

5. Записать выражение для мгновенного значения тока, график которого изображен на рис. 1.5, б, если период колебания Т = 2 с. Определить значение тока в момент времени t1 = T/8.

6. Построить в одной системе координат графики напряжений u1(t) = , u2(t) = .

7. Какая связь между векторным и временным представлением гармонических колебаний?

8. Построить векторы гармонических колебаний, приведенных в п. 6.

9. Построить в одной системе координат графики гармонических колебаний, которым соответствуют векторы и , вращающиеся с одинаковой частотой. Определить сдвиг фаз этих колебаний.

10. Какая связь между параметрами комплексного и временного представления гармонических колебаний?

11. Сформулировать закон Ома для резистивной, индуктивной и емкостной цепей.

12. Какой сдвиг фаз между напряжением и током в резисторе (емкости, индуктивности)?

13. Как рассчитывается комплексное сопротивление последовательного соединения R, L, C элементов?

14. Как рассчитывается комплексная проводимость параллельного соединения R, L, C элементов?

15. Определить комплексное сопротивление цепи, изображенной на рис. 1.55, если

R1 = 20 Ом, R2 = 40 Ом,

Построить треугольник сопротивления цепи.

16. Какие методы используются для расчета цепей с источниками гармонических колебаний?

17. Рассчитать токи в ветвях цепи, изображенной на рис. 1.55, если на вход подается напряжение , В. Построить векторную диаграмму токов.

18. Рассчитать ток Im2 в цепи, изображенной на рис. 1.56, методом наложения и методом эквивалентного генератора, если заданы сопротивления R = 10 Ом, ХL = 30 Ом, ХС = 20 Ом и Um = 10ej0° В, Imг = ej270° А.

19. Что такое комплексный коэффициент передачи? Какие виды комплексных коэффициентов передачи известны?

20. Определить коэффициенты передачи в цепи Примера 1.16, если реакцией является Im2.

* Следует различать резисторы, катушки индуктивности и конденсаторы как физические элементы электрической цепи и резистивные, индуктивные и емкостные элементы как идеализированные элементы, обладающие свойствами необратимого рассеяния энергии или свойствами накопления энергии магнитного и электрического полей. В инженерной практике резистивный, индуктивный и емкостной элементы часто называют просто сопротивлением, индуктивностью и емкостью, отождествляя по существу элемент с его параметром. В дальнейшем для простоты, где это не приведет к недоразумению, мы также будем пользоваться этой терминологией.

💥 Видео

ТРЕУГОЛЬНИК СОПРОТИВЛЕНИЙ RL-ЦЕПИ. Решение задачи 5.50Скачать

Задача на расчет эквивалентного сопротивления цепиСкачать

Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Векторная диаграмма для трехфазной цепи │ТРЕУГОЛЬНИКСкачать

RL ЦЕПЬ │Теория и задача │Переменный токСкачать

Трехфазные электрические цепи │Теория ч. 1Скачать

Построение векторной диаграммы. Цепь RLCСкачать

ОТЦ 2021. Лекция 11. Комплексное сопротивление простых RC и RL цепей.Скачать

КАК РАБОТАЕТ RL - ЦЕПЬСкачать

Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Трехфазные цепи - ТРЕУГОЛЬНИК. Расчет трехфазной цепи, соединенной треугольникомСкачать

Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Соединение трехфазных цепей звездой и треугольникомСкачать

Параллельное соединение RLC элементов │Переменный токСкачать

RL-ЦЕПЬ. Решение задачи 5.39Скачать

Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать