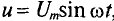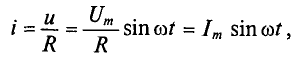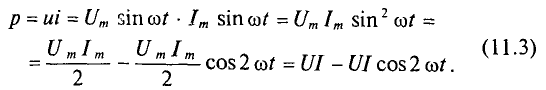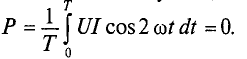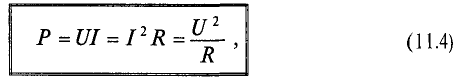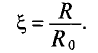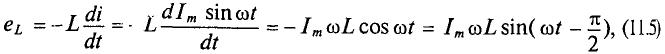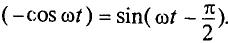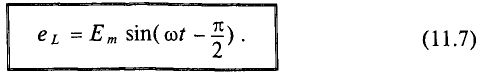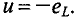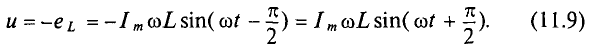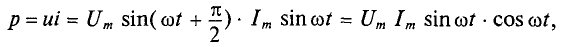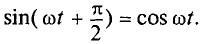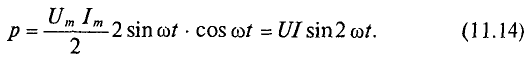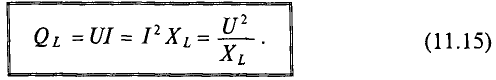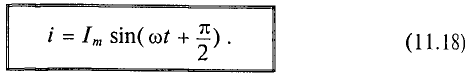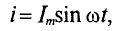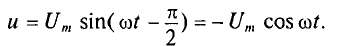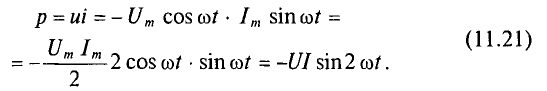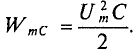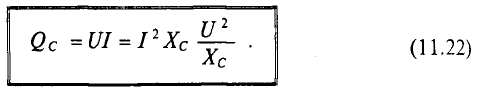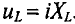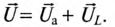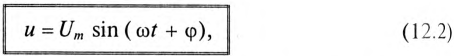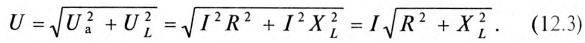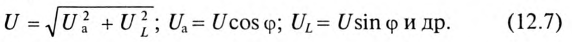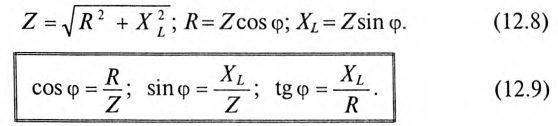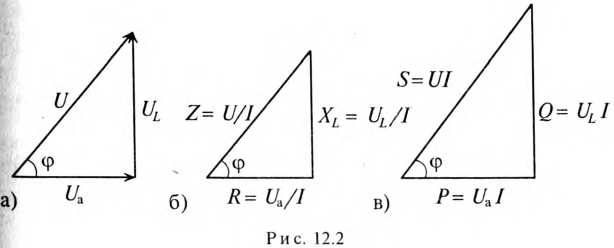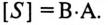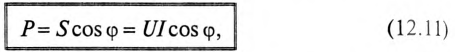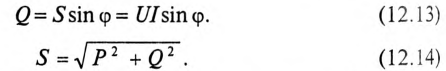Треугольник сопротивлений катушки индуктивности

Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.

Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.

В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.

Видео:R, L, C в цепи переменного тока/Треугольник сопротивлений/Сдвиг по фазеСкачать

Схема замещения катушки с последовательным соединением элементов

В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.

Активное сопротивление определяется величиной мощности потерь

R = P/I 2

а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = I_msinωt. Требуется определить напряжение в цепи и мощность.
При переменном токе в катушке возникает э. д. с. самоиндукции e_L поэтому ток зависит от действия приложенного напряжения и эдс e_L. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:

Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых u_R равно падению напряжения в активном сопротивлении, а другое u_L уравновешивает эдс самоиндукции.

В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — u_R совпадает по фазе с током, U_L опережает ток на 90°.

u = R*I_msinωt + ωLI_msin(ωt+π/2).

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Векторная диаграмма реальной катушки и полное её сопротивление

Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения

а действующие величины

Вектор общего напряжения

Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.

За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.

Вектор U_R по направлению совпадает с вектором тока I, а вектор U_L направлен перпендикулярно вектору I с положительным углом.

Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ 2 Z (13.21)

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):

(13.22)

Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить

cosφ = P/S; sinφ = Q/S; tgφ = Q/P. (13.23)

Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).

Активная мощность Р меньше или равна полной мощности цепи.
Отношение активной мощности цепи к ее полной мощности P/S =
= cosφ называют коэффициентом мощности.

Назначение приемников электрической энергии — преобразование
ее в другие виды энергии. Поэтому колебания энергии в цепи не только
бесполезны, но и вредны, так как при этом в приемнике не совершается
полного преобразования электрической энергии в работу или тепло,
а в соединительных проводах она теряется.

Видео:Откуда взялась формула полного сопротивления цепи? Треугольник напряжений, треугольник сопротивленийСкачать

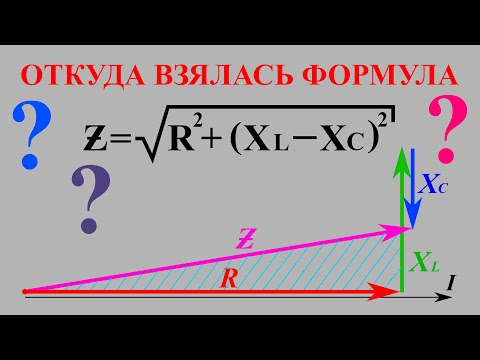
Схема замещения реальной катушки с параллельным соединением элементов

Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной B_L проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.

Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: I_G —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; I_L — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.

Вектор тока I и его составляющие I_G и I_L образуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается I_а. Для катушки по схеме на рис. 13.12, б I_a = I_G.

Составляющая тока в реактивном элементе

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки I_р = I_L .

Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = I_G/U и индуктивная В_L = I_L/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.

Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим

Видео:Индуктивное сопротивлениеСкачать

Электрические цепи синусоидального тока

Содержание:

Видео:Резистор, конденсатор, катушка индуктивности, сравнение свойств в электрических цепяхСкачать

Электрические цепи синусоидального тока:

В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.

При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.

Видео:Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Цепь с активным сопротивлением

Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).

Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение

где

Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны ( 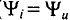= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.

Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 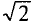=1,41.

Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.

Активная мощность

Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.

Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.

Количественно мощность в цепи с активным сопротивлением определяется следующим образом:

Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 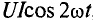, изменяющейся с двойной частотой.

Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть

Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:

где U- действующее значение напряжения; I— действующее значение тока.

Единицей активной мощности является ватт:

Поверхностный эффект и эффект близости

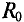
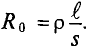
Сопротивление проводника постоянному току называют омическим сопротивлением и определяют выражением (2.8) Сопротивление проводника переменному току R называют активным.

Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.

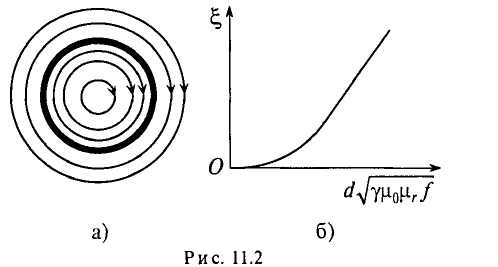
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).

На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.

Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.

Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 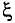(кси)

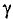
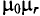
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости , магнитной проницаемости материала проводника и частоты переменного тока , проходящего по проводнику, показан на рис. 11.26.

При токах большой частоты (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.

На величину активного сопротивления проводника R оказывает влияние и эффект близости.

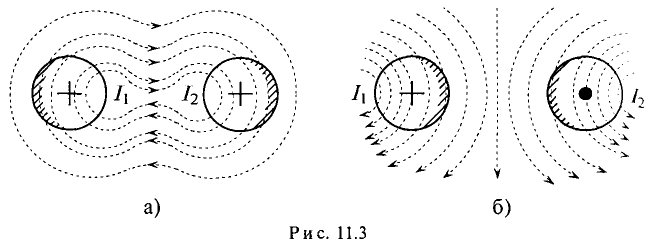
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.

Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).

Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Цепь с идеальной индуктивностью

Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.

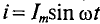
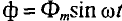
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток , то этот ток создает в катушке синусоидальный магнитный поток , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)

так как

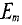
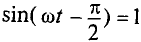
Очевидно, эта ЭДС достигает своего амплитудного значения тогда, когда :

Тогда

Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 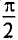(рис. 11.46, в).

По второму закону Кирхгофа для мгновенных значений можно записать

Откуда

Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):

Очевидно, напряжение достигает своего амплитудного значения U_m тогда, когда :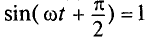

Следовательно,

Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 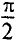(рис. 11.46, в).

Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).

Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 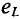противодействует изменению тока.

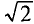
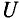
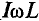
Если уравнение (11.10) разделить на =1,41, то получается =, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением X_L.

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление X_L — это противодействие, которое ЭДС самоиндукции e_L оказывает изменению тока.

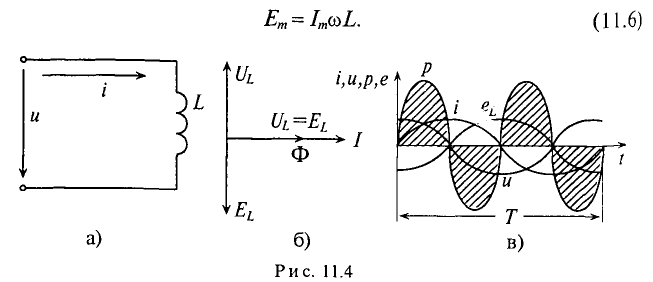
Реактивная мощность в цепи с индуктивностью

Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока

где

Следовательно,

Полученное уравнение умножают и делят на 2:

Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.

Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.

Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (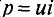) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.

То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно

Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.

Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.

Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.

Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).

Величина реактивной мощности в рассматриваемой цепи определяется выражением

Так как реактивная мощность Q_L имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. X_L.

Видео:Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать

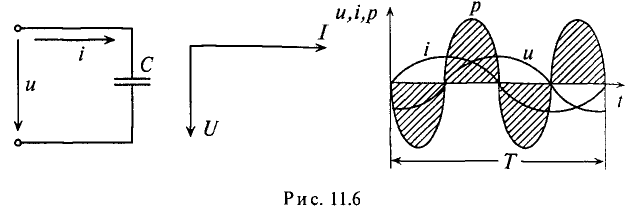
Цепь с емкостью

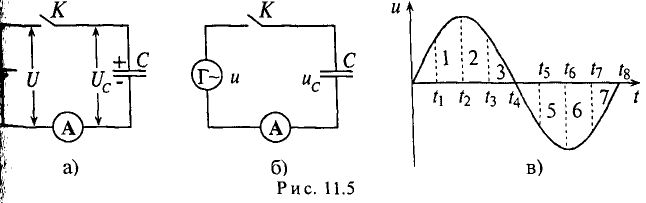
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе U_c не станет равным напряжению источника U.

Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).

Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе U_c отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 — конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 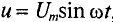, то в цепи конденсатора проходит ток i (рис. 11.6а):

где q= Си согласно (6.3).

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда :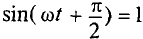

Тогда

Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=

Следовательно, напряжение отстает по фазе от тока на 90° = (рис. 11.66).

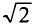
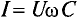
Если уравнение (11.17) разделить на = 1,41, то получится равенство или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.

Очевидно, знаменатель этого равенства является сопротивлением конденсатора Х_с, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).

Реактивная мощность в цепи с конденсатором

Если в цепи конденсатора емкостью 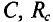= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:

Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно

Мгновенная мощность в цепи с конденсатором

Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).

Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.

Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.

Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно

В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.

Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.

Величина реактивной мощности в цепи конденсатора определяется выражением

Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) — аналитическом выражении мгновенной мощности в цепи с конденсатором.

Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Х_с).

Видео:Последовательное соединение активного сопротивления, индуктивности и емкостиСкачать

Расчет линейных электрических цепей синусоидального тока

Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.

Цепь с активным сопротивлением и индуктивностью

Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 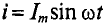(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки

Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

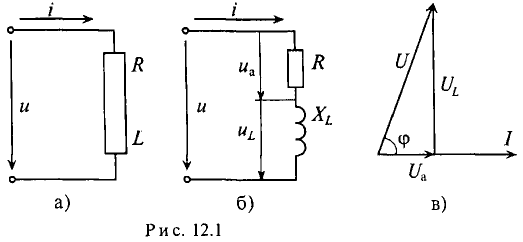
Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением X_L (рис. 12.16).

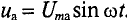
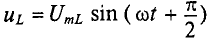
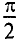
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано . Индуктивное напряжение опережает ток на угол 90° = .

Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 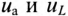согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений

Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).

Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 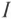на угол ф. Мгновенное значение этого напряжения может быть записано:

где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.

Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.

Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Z_k — полное, или кажущееся, сопротивление реальной катушки.

Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.

Треугольники напряжений, сопротивлений, мощностей

Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).

Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:

Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:

Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).

Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).

Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е.

Однако потребляется в цепи только часть полной мощности — активная мощность

где cos ф показывает, какая часть полной мощности 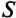потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:

Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.

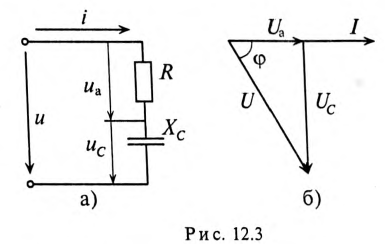
Цепь с активным сопротивлением и емкостью

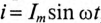
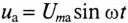
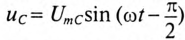
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток , то он создает падение напряжения на активном сопротивлении и на емкостном сопротивлении . Векторная диаграмма для этой цепи изображена на рис. 12.36.

Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Урок 28. КАТУШКА ИНДУКТИВНОСТИ в цепи переменного токаСкачать

Свойства активного и реактивного сопротивления

В электротехнике понятие сопротивления представляет собой величину, за счет которой определенная часть цепи может противодействовать электрическому току. Она образуется за счет изменения и перехода электроэнергии в другое энергетическое состояние. Данное явление присуще только переменному току, когда в сети образуется активное и реактивное сопротивление, выражающееся в необратимом изменении энергии или передаче этой энергии между отдельными компонентами электрической цепи. В случае необратимых изменений электроэнергии сопротивление будет считаться активным, а при наличии обменных процессов – реактивным.

Видео:ИндуктивностьСкачать

Основные различия между активным и реактивным сопротивлением

Когда электрический ток проходит через элементы с активным сопротивлением, происходят необратимые потери выделяемой мощности. Типичным примером служит электрическая плита, где в процессе работы происходят необратимые превращения электричества в тепловую энергию. То же самое происходит с резистором, в котором тепло выделяется, но обратно в электроэнергию не превращается.

Помимо резисторов, свойствами активного сопротивления обладают приборы освещения, электродвигатели, трансформаторные обмотки, провода и кабели и т.д.

Характерной особенностью элементов с активным сопротивлением являются напряжение и ток, совпадающие по фазе. Рассчитать этот параметр можно по формуле: r = U/I. На показатели активного сопротивления оказывают влияние физические свойства проводника – сечение, длина, материал, температура. Эти качества позволяют различать реактивное и активное сопротивление и применять их на практике.

Реактивное сопротивление возникает в тех случаях, когда переменный ток проходит через так называемые реактивные элементы, обладающие индуктивностью и емкостью. Первое свойство характерно для катушки индуктивности без учета активного сопротивления ее обмотки. В данном случае причиной появления реактивного сопротивления считается ЭДС самоиндукции. В зависимости от частоты тока, при ее возрастании, наблюдается и одновременный рост сопротивления, что отражается в формуле xl = wL.

Видео:ДЛЯ ЧЕГО НУЖНА КАТУШКА ИНДУКТИВНОСТИ? #катушка #индуктивность #электроникаСкачать

Сравнение влияния реактивного сопротивления на активную мощность сети

Из рисунков 1 и 2 видно, что сдвиг фаз на рисунках не одинаков. Вывод — чем больше в полном сопротивлении Z будет влияние XL или XC тем больше будет разница фаз U и I.

Угол сдвига между током и напряжением называется φ .

Реактивная мощность однофазная:

Uф, Iф — фазные ток и напряжение

Вывод: реактивная мощность – не выполняет полезного действия.

Она «перегоняется» по сети нагревая кабели и увеличивая потери. На крупных промышленных предприятиях это особо ощутимо в силу наличия электроприводов и других крупных потребителей. Этот вопрос очень актуален для энергосбережения и модернизации производства. Поэтому на пром. предприятиях устанавливаются компенсаторы реактивной мощности. Они могут быть разного типа и кроме компенсации выполнять еще и роль фильтров. С помощью компенсаторов стараются сохранить баланс реактивной мощности для минимизации ее влияния на сеть и подогнать угол φ к нулю.

Для компенсации реактивной мощности необходимо максимально сбалансировать в сети количество (L, C) элементов.

Видео:Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать

Индуктивное сопротивление

Реактивное сопротивление подразделяется на два основных вида – индуктивное и емкостное.

При рассмотрении первого варианта следует отметить возникновение в индуктивной обмотке магнитного поля под действием переменного тока. В результате, в ней образуется ЭДС самоиндукции, направленной против движения тока при его росте, и по ходу движения при его уменьшении. Таким образом, при всех изменениях тока и наличии взаимосвязей, ЭДС оказывает на него противоположное действие и приводит к созданию индуктивного сопротивления катушки.

Под влиянием ЭДС самоиндукции энергия магнитного поля обмотки возвращается в электрическую цепь. То есть, между источником питания и обмоткой происходит своеобразный обмен энергией. Это дает основание полагать, что катушка индуктивности обладает реактивным сопротивлением.

В качестве типичного примера можно рассмотреть действие реактивного сопротивления в трансформаторе. Данное устройство имеет общий магнитопровод, с расположенными на нем двумя обмотками или более, имеющими общую зависимость. На одну из них поступает электроэнергия из внешнего источника, а из другой выходит уже трансформированный ток.

Под действием первичного тока, проходящего по катушке, в магнитопроводе и вокруг него происходит наведение магнитного потока. В результате пересечения витков вторичной обмотки, в ней формируется вторичный ток. При невозможности создания идеальной конструкции трансформатора, магнитный поток будет частично уходить в окружающую среду, что приведет к возникновению потерь. От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.

Видео:Активное и реактивное сопротивление цепи переменного тока. 11 класс.Скачать

Разновидности катушек индуктивности

Контурные катушки индуктивности

Эти катушки используются совместно с конденсаторами для получения резонансных контуров. Они должны иметь высокую стабильность, точность идобротность .

Такие катушки применяются для обеспечения индуктивной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току цепи базы иколлектора и т. д. К таким катушкам не предъявляются жёсткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи.

Это катушки, индуктивность которых можно изменять в процессе эксплуатации для перестройки колебательных контуров. Они состоят из двух катушек, соединённых последовательно. Одна из катушек неподвижная (статор), другая располагается внутри первой и вращается (ротор). При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра. Такая система позволяет изменять индуктивность в 4 − 5 раз. В ферровариометрах индуктивность изменяется перемещением ферромагнитного сердечника.

Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному. Обычно включаются в цепях питания усилительных устройств. Предназначены для защиты источников питания от попадания в них высокочастотных сигналов. На низких частотах они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники.

две намотанных встречно катушки индуктивности, используются в фильтрах питания. За счёт встречной намотки и взаимной индукции более эффективны при тех же габаритных размерах. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания; в дифференциальных сигнальных фильтрах цифровых линий, а также в звуковой технике.

Видео:Что такое ИМПЕДАНС | РЕАКТИВНОЕ СОПРОТИВЛЕНИЕСкачать

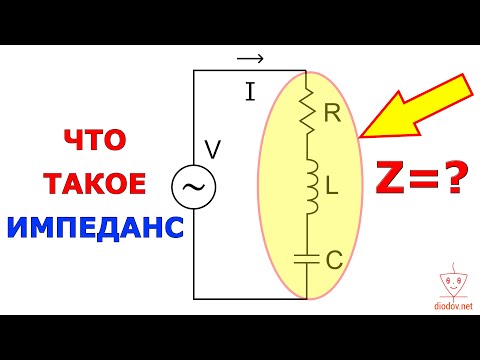
Емкостное сопротивление

В цепи, содержащей емкость и источник переменного тока происходят изменения заряда. Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.

В конструкцию конденсатора входят токопроводящие пластины в количестве двух и более штук, разделенных слоями диэлектрика. Такое разделение не позволяет постоянному току проходить через конденсатор. Переменный ток может проходить через емкостное устройство, отклоняясь при этом от своей первоначальной величины.

Изменения переменного тока происходят под влиянием емкостного сопротивления. Чтобы лучше понять схему работы, найдем и рассмотрим принцип действия данного явления. Переменное напряжение, приложенное к конденсатору, изменяется в форме синусоиды. Под его воздействием на обкладках наблюдается всплеск, одновременно здесь накапливаются заряды электроэнергии с противоположными знаками. Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.

В момент изменения полупериода колебания, напряжение на обкладках конденсатора меняет свою полярность на противоположное значение, потенциалы также изменяются, а заряды пластин перезаряжаются. За счет этого удается создать течение первичного тока и находить способ противодействовать его прохождению, при уменьшении величины и сдвиге угла. Зарядка обкладок позволяет току, проходящему через конденсатор, опережать напряжение на 90.

Видео:АКТИВНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ | ОБЪЯСНЯЮ НА ПАЛЬЦАХСкачать

Устройство катушки

Катушку изготавливают путем наматывания на цилиндрический или тороидальный каркас провода в изоляции. Изоляция — обязательный атрибут, без нее из-за межвиткового замыкания, катушка превратится в обычный проводник.

На концах намотанного провода устанавливают контакты. С их помощью катушка индукции подключается в цепь последовательно с нагрузкой. Внутрь каркаса может помещаться металлический сердечник.

При изготовлении катушки провод наматывают двумя способами:

1. в один слой: такую обмотку называют «рядовой с шагом»;
2. в несколько слоев: способ обозначают терминами «внавал» или «универсал».

Расстояние, на которое витки провода отстоят друг от друга, называется шагом. При намотке некоторых катушек шаг постепенно увеличивают (прогрессивный шаг), чем добиваются снижения паразитной емкости.

Видео:Катушка индуктивности в цепи переменного токаСкачать

Полное сопротивление[ | ]

Как реактивное сопротивление X <displaystyle scriptstyle > так и обычное сопротивление R <displaystyle scriptstyle > компоненты импеданса Z <displaystyle scriptstyle > .

• Z — импеданс, измеряемый в омах;
• R — сопротивление, измеряемый в омах. Это также реальная часть импеданса: R = ℜ ( Z ) <displaystyle <R=Re >>
• X — реактанс, измеряемый в омах. Это также мнимая часть импеданса: X = ℑ ( Z ) <displaystyle <X=Im >>
• j — мнимая единица, чтобы отличать от тока, который обозначается обычно i .

Когда и конденсатор и индуктор соединены последовательно в цепь, их вклады к полному импедансу цепи противоположны. Ёмкостное сопротивление X C <displaystyle scriptstyle <X_>> , и индуктивное сопротивление X L <displaystyle scriptstyle <X_>> ,

вносят свой вклад в общее реактивное сопротивление X <displaystyle scriptstyle > в виде суммы

• X L <displaystyle scriptstyle <X_>> — индуктивное сопротивление, измеряемое в омах;
• X C <displaystyle scriptstyle <X_>> — ёмкостное сопротивление, измеряемое в омах;
• ω — угловая частота, 2 π умноженная на частоту в Гц.

• если X > 0 0> , то реактанс имеет вид индуктивности;
• если X = 0 , импеданс чисто реальный;
• если X

🔥 Видео

катушка индуктивности в цепях постоянного и переменного токаСкачать

3 3 Катушка индуктивности в цепи переменного синусоидального токаСкачать

Урок №8. Катушка индуктивностиСкачать