О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Никогда не торгуй эту фигуру! И знакомым запрети!Скачать

Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Видео:Паттерн треугольник в трейдинге - Одна из самых часто встречаемых фигур на графикеСкачать

Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Видео:Технический анализ треугольник [Артём Звёздин]Скачать
![Технический анализ треугольник [Артём Звёздин]](https://i.ytimg.com/vi/G5ZIXR5fBPU/0.jpg)
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
| x | y |
| 0 | -1 |
| 1 | 2 |
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 0 | 2 |
| 1 | 1 |
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Видео:Математика это не ИсламСкачать

Графики элементарных функций
Прямая линия — график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a
Парабола — график функции квадратного трёхчлена у = ах 2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а 2 + bx +с =0
Гипербола — график функции 
Экспонента (показательная функция по основанию е) у = е x . (Другое написание у = ехр(х)). Асимптота — ось абсцисс.
Логарифмическая функция y = logax (a > 0)
у = sinx. Синусоида — периодическая функция с периодом Т = 2π
у = а•sin(ωx+φ) — функция гармонических колебаний. Обозначения: а — амплитуда, ω — частота (ω = 2π/Т), φ — фаза (сдвиг).
Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на 
Тангенсоида y = tgx. Точки разрыва при х = 
Гауссиана у = Аe -(ax 2 ) . Кривая «нормального» закона распределения ошибок, у которого


σ 2 — дисперсия ошибки. Симметрия относительно оси у.
у = secx — кривая «цепной линии», эту форму принимает абсолютно гибкая нить, подвешенная в параллельном поле тяжести. А полная функция периодична, и её асимптоты х = 
Затухающее колебание y = Ae -ax •sin(ωx+φ)
Квадратный корень — элементарная функция и частный случай степенной функции 


Как функция комплексного переменного корень — двузначная функция, листы которой соединяются в нуле.
Кубический корень — нечётная функция.
Функция модуль является четной функцией. Производная функции модуль в точке x=0 не существует. График функции модуль симметричен относительно оси ординат.
Видео:Что Такое Фракталы? Простое Объяснение!Скачать

Технический анализ. Треугольники. Часть первая
Среди фигур технического анализа треугольники занимают почётное место. Есть несколько видов треугольников. Они достаточно часто встречаются на графиках и в основном служат признаками продолжения тенденции, но при определённых обстоятельствах указывают на разворот.
Фигуры продолжения обычно означают, что период коррекции является не более чем паузой в развитии основной тенденции и направление движения цен останется прежним после их завершения.
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Симметричный треугольник
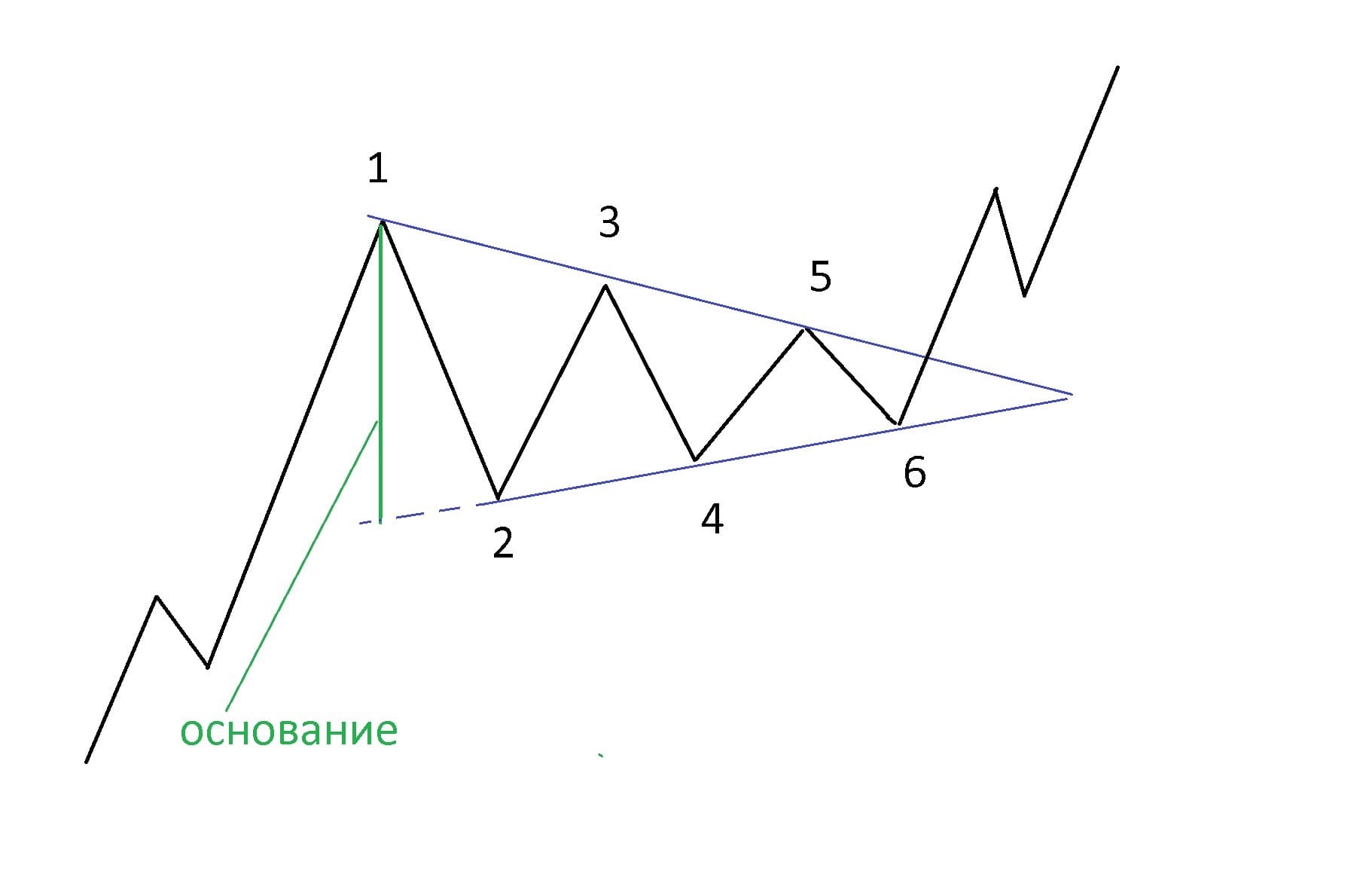
Этот тип треугольников образуется двумя сходящимися линиями, где верхняя линия опускается, а нижняя поднимается. В данном случае не стоит придавать слову «симметричный» такой же смысл, как в геометрии, то есть линии, образующие треугольник, не обязательно будут равны.
Минимальным требованием для построения любого треугольника является наличие четырёх точек — две сверху и две снизу. В действительности треугольники могут иметь шесть таких точек.
«Симметричный треугольник», как правило, является фигурой продолжения тенденции.
Высота, проведённая из точки 1 к продолжению нижней линии, называется основанием треугольника, а точка пересечения линий — это вершина. Фигура сохраняется до тех пор, пока цена не пробьёт одну из линий. При выходе нередко цена возвращается к пробитой линии, отбой от которой позволяет присоединиться к начавшемуся движению.
Выход цены из треугольника должен быть в пределах от 50% до 75% ширины треугольника по горизонтали.
Под шириной треугольника понимается расстояние от основания фигуры до её вершины.
Если цены не вышли из треугольника в этих пределах, фигура начинает терять свой потенциал.
Это означает, что цены продолжат движение к вершине треугольника, а затем — дальше, за её пределы. При этом боковая тенденция сохраняется и принимает иную форму, но опираться в анализе на эту фигуру уже не стоит.
Видео:ВОСХОДЯЩИЙ И НИСХОДЯЩИЙ ТРЕУГОЛЬНИК | Паттерны для новичков | Технический анализ для начинающихСкачать

Построение целевых ориентиров
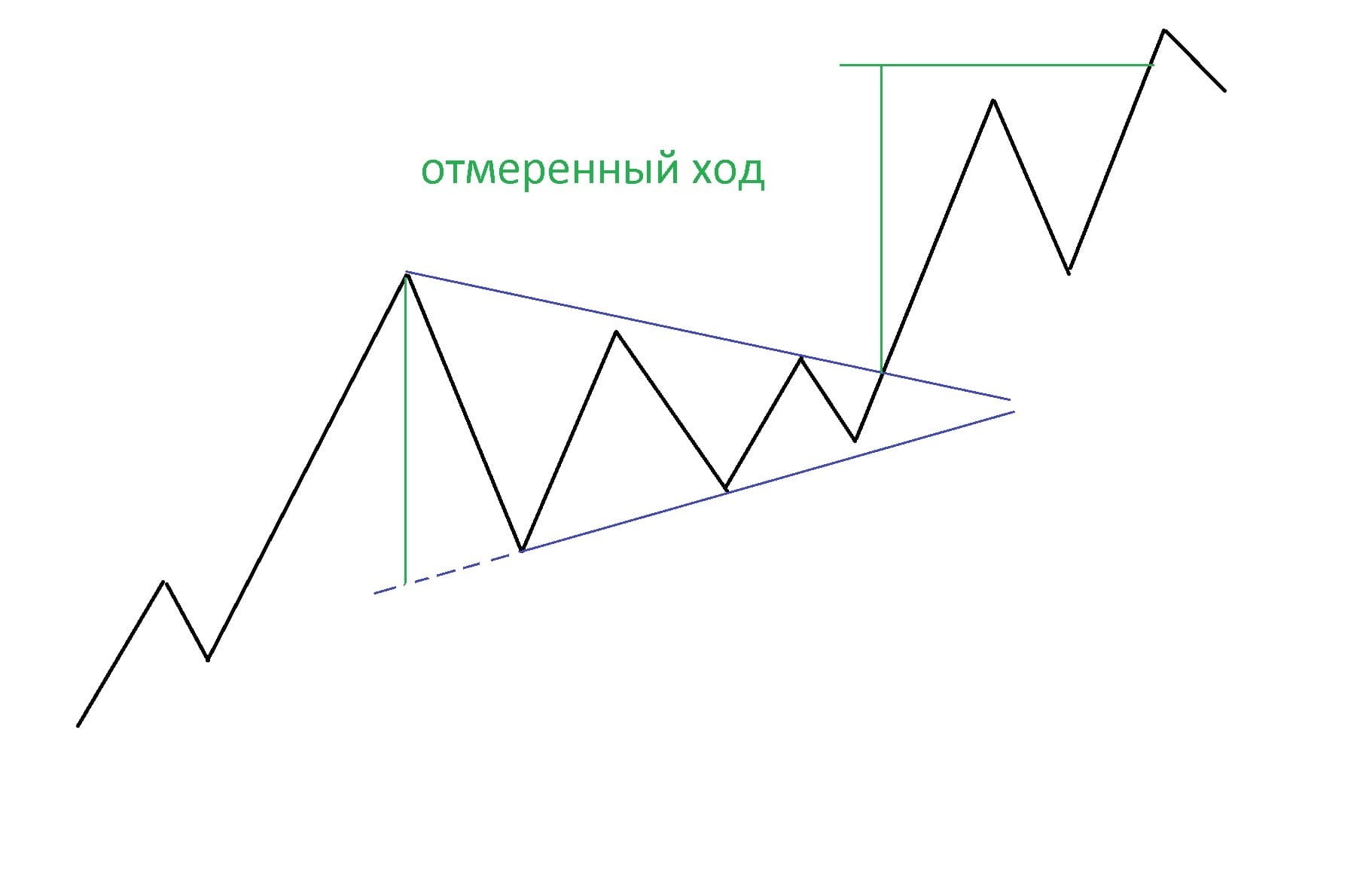
Существует два способа определения цели для движения цены после пробоя. Один из них уже известен и состоит в измерении высоты основания, которая затем откладывается от точки пробоя.
Этот способ уже был описан ранее в статье про фигуру «Голова и плечи».
Другой способ позволяет построить цель, проводя параллельную линию из точки основания треугольника.
Этот способ аналогичен построению границ канала. Из вершины 1 проводится линия параллельно линии поддержки в треугольнике.
Оба способа построения цели равновесны, поэтому их можно использовать одновременно.
Не забываем о том, что построение цели на графиках — это лишь предположение и не обязывает цену поступать соответствующе.
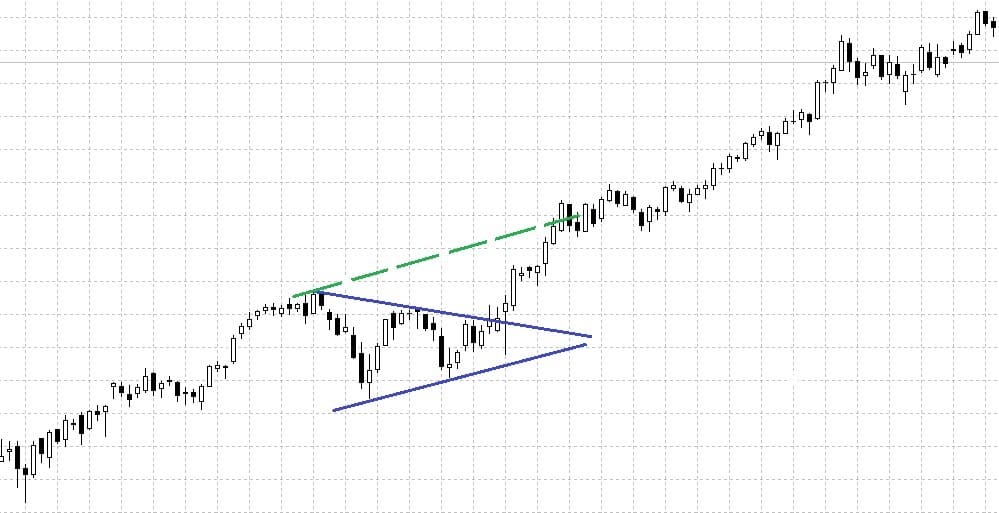
На восходящем движении образуется коррекция. Её форма соответствует фигуре «Симметричный треугольник», указывающей на продолжение роста. Ценовой ориентир получаем первым способом, измеряя высоту основания и откладывая её от точки пробоя.
В данном случае цель определена вторым способом. Из основания треугольника проведена линия параллельно нижней границе треугольника.
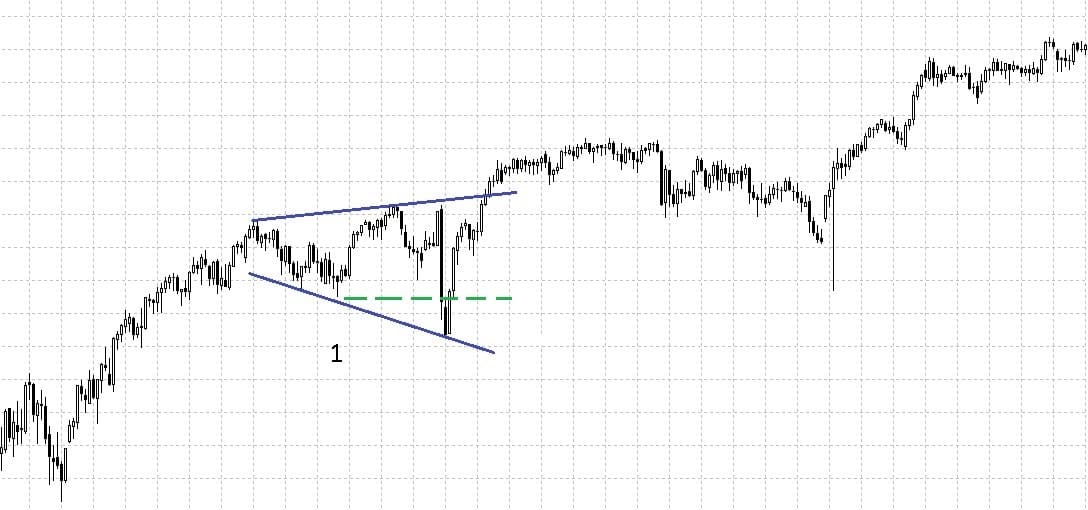
Симметричный треугольник на падающем рынке также выступает фигурой продолжения. Имеет аналогичные свойства и характеристики.
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Расширяющийся треугольник
Этот вид треугольников отличается от симметричного тем, что начинается с вершины и движется к основанию, увеличивая размах колебания. Линии, ограничивающие его, как и у «Симметричного треугольника», расходятся в разные стороны.
Использование этих треугольников иное, нежели симметричных. Основная проблема этого вида коррекций именно в том, что размах колебания увеличивается. Новый максимум создаёт ложный сигнал на рост, а пробой уровня коррекции в точке 1 создаёт ложный ориентир на падение. Построить цель из фигуры проблематично.
Расширяющийся треугольник нередко становится фигурой разворота.
Спекулянты, торгующие с плечом, шутят, что расширяющийся треугольник — это пила, которая перепилит любой депозит.
В следующей статье мы рассмотрим другие виды треугольников.
Информация, представленная в статье, не является призывом или рекомендацией к действию. Принимая решение совершать торговые операции на финансовых рынках, вы в полной мере осознаёте и принимаете на себя все риски.
При подготовке данного цикла статей были использованы материалы из книг: Дж. Швагер «Технический анализ. Полный курс», Т. Р. Демарк «Технический анализ — новая наука», С. Нисон «Японские свечи», Г. Моррис «Японские свечи».
С теорией всё более-менее понятно, а что насчёт практики? Откройте брокерский счёт онлайн в «Открытие Брокер» и начинайте торговать прямо сейчас! А мы поможем советами и рекомендациями — всё самое полезное каждую неделю будет приходить прямо на ваш email, если подпишетесь на рассылку.
Без минимальной суммы, платы за обслуживание и скрытых комиссий
проект «Открытие Инвестиции»
Москва, ул. Летниковская, д. 2, стр. 4
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
📺 Видео
Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

ПАТТЕРН ТРЕУГОЛЬНИК В ТРЕЙДИНГЕ - ВСЯ СУТЬ!Скачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Производная: Разбираем её Геометрический и Физический СмыслСкачать

СИММЕТРИЧНЫЙ ТРЕУГОЛЬНИК В ТРЕЙДИНГЕ Как Находить? Как Правильно Использовать? на Бинарных Опционах!Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Как построить точки в системе координат OXYZСкачать

Математический анализ, 15 урок, АссимптотыСкачать

Фигуры теханализа на которых крупняк обманывает толпу. Фигуры трейдинга треугольникСкачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать








 при х ≠ -1.
при х ≠ -1.






 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0. , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b