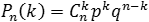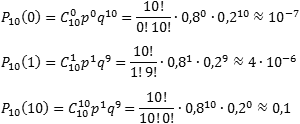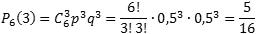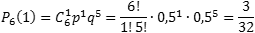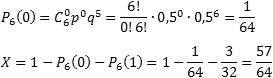Треугольник эйлера бернулли задачи

Не будем долго размышлять о высоком — начнем сразу с определения.

— это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A , причем известна вероятность этого события P ( A ) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

1. A — появление события A с вероятностью p;
2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A , которое возникает с одной и той же вероятностью p.

Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C _n k — число сочетаний, q = 1 − p.

Эта формула так и называется: . Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A », т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные ( k = 0), что только одна деталь без брака ( k = 1), и что бракованных деталей нет вообще ( k = 10):

Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:

1. герб выпадет три раза;
2. герб выпадет один раз;
3. герб выпадет не менее двух раз.

Итак, нас интересует событие A , когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A », когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.

Таким образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим вероятность того, что герб выпал три раза, т.е. k = 3:

Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:

Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k , кроме 0 и 1, т.е. надо найти значение суммы X = P ₆(2) + P ₆(3) + . + P ₆(6).

Заметим, что эта сумма также равна (1 − P ₆(0) − P ₆(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз ( k = 1) или не выпал вообще ( k = 0). Поскольку P ₆(1) нам уже известно, осталось найти P ₆(0):

Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?

Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.

Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.

Найдем вероятность получить два «дефектных» телевизора ( k = 2) и три ( k = 3):

Очевидно, P ₂₀(3) > P ₂₀(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.

Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.

P . S . А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.

Видео:Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Методические указания для выполнения практической работы «Вычисление вероятностей событий в схеме Бернулли».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Министерство образования и науки Самарской области

Государственное бюджетное образовательное

учреждение среднего профессионального образования

«Тольяттинский политехнический техникум»

Зам. директора по УР

___________ C .А.Гришина

__ _________ 20__ г.

для выполнения практической работы №5

«Вычисление вероятностей событий в схеме Бернулли»

дисциплина Теория вероятностей и математическая статистика

специальностей: 09.02.06 Сетевое и системное администрирование

09.02.07 Информационные системы и программирование

от ___ _____20__ № ____

Руководитель УПО №2

________ Л.Г. Светличная

___ ______ 20__

Методические указания разработаны Захаровой С.В. – преподавателем

математических дисциплин ГБПОУ СО «ТПК».

Методические указания предназначены для студентов второго курса дневного отделения специальностей 09.02.06 «Сетевое и системное администрирование», 09.02.07 «Информационные системы и программирование». Методические указания составлены в соответствии с рабочей программой и могут быть использованы с целью формирования практических умений и навыков при изучении темы «Вычисление вероятностей событий в схеме Бернулли».

Практическая работа №5

Тема: «Вычисление вероятностей событий в схеме Бернулли»

• научиться вычислять вероятности событий с помощью формулы Бернулли

В результате выполнения практической работы студент должен:

• вычислять вероятности событий с помощью формулы Бернулли.

Краткие теоретические сведения

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;

2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой.

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р , т.е. p=P(A) , а вероятность противоположного события (событие А не наступило) — буквой q=P( )=1−p .

Тогда вероятность того, что событие А появится в этих n испытаниях ровно m раз, выражается формулой Бернулли

Распределение числа успехов (появлений события) носит название биномиального распределения .

Образец решения задач

1. В семье 3 детей. Найти вероятность того, что среди этих детей 2 мальчика. Вероятность рождения мальчика равна 0,8.

Нужно найти, что родится мальчик.

p = 0,8 – вероятность рождения мальчика,

q =1-0,8=0,2 – вероятность рождения девочки.

Используем формулу Бернулли:

Ответ: вероятность рождения мальчика 0,384

2. В цеху имеются 4 резервных мотора. Для каждого мотора вероятность того, что он включён, равна 0,3. Найти вероятность того, что в данный момент 3 мотора выключены.

Нужно найти, что 3 мотора выключены.

p = 1-0,3=0,7 – вероятность того, что мотор выключен,

q =0,3 – вероятность того, что мотор включён.

Ответ: вероятность того, что мотор выключен, равна 0,4116

3. Прибор состоит из 6 узлов. Вероятность безотказной работы каждого узла равна 0,8. Узлы выходят из строя независимо друг от друга. Найти вероятность того, что за некоторое время откажут 2 узла.

Нужно найти, что 2 узла откажут.

p =0,2 – вероятность отказа узла,

q =0,8 – вероятность безотказной работы узла.

Ответ: вероятность того, что за некоторое время откажут 2 узла, равна 0,2457

4. В партии 10 деталей Вероятность отклонения от наминала равна 0,4. Найти вероятность того, что в данной партии есть 5 деталей без отклонения от наминала.

Нужно найти, что 5 деталей без отклонения от наминала.

p =0,6 – вероятность без отклонения от наминала,

q =0,4 – вероятность отклонения от наминала.

Ответ: вероятность того, что в данной партии есть 5 деталей без отклонения от наминала, равна 0,20066.

5. Вероятность всхожести семян в среднем составляет 0,8. Найти вероятность того, что из 7 семян взойдёт более 5. Решение:

Нужно найти, что что из 7 семян взойдёт более 5 ( или 6 семян, или 7 ).

p =0,8 – вероятность всхожести семян,

q =0,2 – вероятность не всхожести семян.

Искомая вероятность равна

Ответ: вероятность того, что из 7 семян взойдёт более 5, равна 0,57671.

6. Пять стрелков производят по одному выстрелу по мишени. Вероятность попадания в мишень для каждого стрелка 0,9. Найти вероятность того, что в мишени будет не менее 4 пробоин.

В мишени будет не менее 4 пробоин из 5 выстрелов ( т. е. или 4 пробоины, или 5)

p = 0,7 – вероятность попадания в мишень,

q =0,3 – вероятность промаха.

Искомая вероятность равна

Ответ: вероятность того, что в мишени будет не менее 4 пробоин, равна 0,52822.

7. В ящике 5 разноцветных шаров. Вероятность вынуть белый шар равна 0,4. Найти вероятность вытащить не менее 2 раз белый шар из 4 попыток.

Вытащить не менее 2 раз белый шар из 4 попыток ( т. е. или 2 раза, или 3 раза, или 4 )

p = 0,4 – вероятность попадания в мишень,

q =0,6 – вероятность промаха.

Искомая вероятность равна

Ответ: вероятность вытащить не менее 2 раз белый шар из 4 попыток равна 0,5248.

8. Монету бросают 2 раза. Найти вероятность того, что «герб» выпадает хотя бы раз.

Герб выпадет хотя бы раз (т. е. или раз из двух, или два из двух)

p = 0,5 – вероятность того, что выпадет герб,

q =0,5 – вероятность того, что выпадет решка.

Найдём вероятность того, что герб не выпадет ни разу, т. е. 0 раз из двух бросаний.

p = 0,5 – вероятность того, что выпадет герб ,

q =0,5 – вероятность того, что выпадет решка.

Искомая вероятность равна

Ответ: вероятность того, что «герб» выпадает хотя бы раз, равна 0,75.

9. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Событие А – достали белый шар. Тогда вероятности
, .
По формуле Бернулли требуемая вероятность равна
.

10. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.

Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А — «появление нестандартной детали», его вероятность , тогда . Отсюда по формуле Бернулли находим
.

11. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.

Решение : Вычисляем по формуле Бернулли:

Задания для самостоятельного решения

Практическая работа №4

Тема: «Вычисление вероятностей событий в схеме Бернулли»

1. Прибор состоит из 10 узлов. Вероятность безотказной работы каждого узла равна 0,8. Узлы выходят из строя независимо друг от друга. Найти вероятность того, что за некоторое время откажут 2 узла.

1. В партии 10 деталей Вероятность отклонения наминала равна 0,4. Найти вероятность того, что в данной партии есть 5 деталей с отклонением от наминала.

1. Монету бросают 6 раз. Найти вероятность того, что «герб» выпадает хотя бы два раза.

1. В семье 5 детей. Найти вероятность того, что среди этих детей более трёх мальчиков. Вероятность рождения мальчика равна 0,7.

1. Вероятность того, что расход электроэнергии за сутки превышает установленную норму равна 0,3. Найти вероятность того, что за 10 суток расход электроэнергии в течении суток не превысит нормы.

Видео:132 Змеи, или Треугольник Бернулли—ЭйлераСкачать

«24 февраля 2012 г. Памяти Филиппа Флажоле Дискретную математику можно определить как науку, изучающую конечные множества. При таком определении она становится . »

Введение в дискретную математику

24 февраля 2012 г.

Памяти Филиппа Флажоле

Дискретную математику можно определить как науку, изучающую конечные множества. При таком определении она становится всепроникающей трудно представить себе раздел математики, не связанный с конечными множествами, и необъятной. Поэтому всякий курс дискретной математики, как начальный, так и более сложный, поневоле ограничивается какими-то аспектами этой науки. Выбор излагаемых аспектов обычно опирается на вкусы автора. В настоящем курсе я следовал своим пристрастиям и исследовательскому опыту. Я также стремился связать курс дискретной математики с другими математическими курсами. Так, изучение производящих функций поддерживает изучение разложений функций в ряд в курсе математического анализа.

Курс разбит на три части. Первые две посвящены перечислительной комбинаторике и графам. В третей, посвященной конечным автоматам, формальным языкам и грамматикам, дается представление о том, как подходы, описанные в первых двух частях, могут применяться для построения простейших вычислительных моделей. В свою очередь, эти модели дают новые подходы к решению перечислительных задач. В приложениях даются решения задач, сопровождающих каждую главу, и образцы контрольных и экзаменационных работ.

Разумеется, вводный характер изложения сказывается и на содержании каждой из частей. Так, из всего богатства результатов о конечных графах я излагаю лишь начальные сведения об их перечислении и инвариантах. В то же время я стремился к тому, чтобы в изложении присутствовал материал, активно используемый в современных математических исследованиях, например в топологии и статистической физике.

При работе с конечными объектами конечными множествами, графами, словами и т.д. ключевую роль играют действующие на них группы, в первую очередь, симметрические группы, или группы перестановок. Любые другие конечные группы являются подгруппами в группах перестановок.

Свойства объектов в значительной мере определяются комбинаторикой соответствующих групп, что позволяет этим группам играть связующую роль между частями книги. Оказывается, однако, что несмотря на многолетние усилия по изучению конечных групп, даже в комбинаторике симметрических групп остается много неизведанного, а некоторые вопросы еще и не поставлены.

В основе первой части книги лежат мои “Лекции о производящих функциях” (первое издание вышло в 2002 г. при поддержке РФФИ, в 2007 г.

издательство Московского центра непрерывного математического образования выпустило их 4-м изданием, а в 2003 г. в издательстве Американского математического общества вышел их перевод на английский язык).

Эти лекции читались первокурсникам Независимого Московского университета. Для курса “Введение в дискретную математику”, который читается на факультете математики Высшей школы экономики во втором семестре первого года обучения, они были существенно переработаны, расширены и i обогащены новыми задачами. Помимо отдельных параграфов в эту часть вошла новая глава про теневое исчисление.

В разные годы вместе со мной этот курс вели Г. Л. Рыбников, А. И. Зыкин и П. Н. Пятов. Многие задачи в том числе для контрольных и экзаменационных работ предложены ими, и я им очень благодарен. П. Н. Пятов кроме того написал решения целого ряда задач. Я также благодарен студентам факультета математики ВШЭ, живая реакция которых позволила, я надеюсь, заметно улучшить первоначальные записки лекций.

Некоторые разделы курса рассчитаны на студентов, уровень подготовки которых выше среднего. Сюда относятся, в первую очередь, вопросы, связанные со структурами алгебр Хопфа на пространствах многочленов и пространствах графов. Остальной материал не опирается на эти структуры, и их изучение можно безболезненно опустить.

ii Оглавление I Элементы перечислительной комбинаторики 1 Элементарные производящие функции 1.1 Перестановки и сочетания. 1.2 Бином Ньютона. 1.3 Экспонента. 1.4 Производящие функции и действия над ними. 1.5 Дифференцирование и интегрирование производящих функций 1.6 Алгебра и топология формальных степенных рядов. 1.7 Задачи. 2 Рациональные производящие функции 2.1 Геометрическая прогрессия. 2.2 Последовательность Фибоначчи. 2.3 Рекуррентные соотношения и рациональные производящие функции. 2.4 Неоднородные рекуррентные соотношения. 2.5 Произведение Адамара рациональных производящих функций 2.6 Асимптотика коэффициентов рациональных функций. 2.7 Задачи. 3 Перечисление путей на графах 3.1 Пути в графах. 3.2 Пути, перечисляемые рациональными производящими функциями. 3.3 Числа Каталана. 3.4 Задачи. 4 Производящие функции нескольких переменных 4.1 Треугольник Паскаля. 4.2 Экспоненциальные производящие функции. 4.3 Треугольник Дика. 4.4 Треугольник Бернулли–Эйлера и перечисление up-down перестановок. 4.5 Числа Эйлера в треугольнике Дика с кратностями. iii 4.6 Производящая функция для треугольника Дика с кратностями 4.7 Задачи. 5 Теневое исчисление 5.1 Определения и примеры. 5.2 Применения биномиальных последовательностей. 5.3 Биномиальные последовательности и сдвиги. 5.4 Явное построение биномиальных последовательностей. 5.5 Последовательности Шеффер. 5.6 Коалгебра многочленов. 5.7 Задачи. 6.3 Разбиения множеств в треугольнике Моцкина с кратностями 13 Языки и формальные грамматики с однозначным выводом 13.2 Формальные грамматики с однозначным выводом. 13.3 Производящие функции регулярных языков. 13.4 Представления производящих функций в виде непрерывных 13.5 Сравнения в последовательностях. Элементы перечислительной комбинаторики Глава Элементарные производящие функции В первой части курса мы займемся задачами перечисления. Они заключаются в подсчете числа объектов, принадлежащих некоторому семейству конечных множеств. У каждого множества семейства имеется свой номер, и результатом перечисления служит некоторая последовательность натуральных чисел. Перечислительные задачи встречаются во всех областях математики, и в последние годы они вышли на первый план в алгебраической геометрии, топологии, многих направлениях математической физики.

Как правило, задача перечислительной комбинаторики “в принципе” разрешима: для каждого множества из семейства можно выписать все его элементы и таким образом узнать их число. Проблема, однако, состоит в том, чтобы найти “хорошее” решение, не требующее выписывания всех элементов изучаемых множеств. При этом понять, что такое хорошее решение, довольно трудно. Зачастую удается лишь сравнить два решения и сказать, какое из них лучше.

Наиболее подходящим языком для решения перечислительных задач оказывается язык производящих рядов. Операции с комбинаторными объектами очень естественно выражаются в терминах производящих функций. Однако перечислительная комбинаторика не сводится к производящим функциям привлечение методов из смежных областей математики (например, из анализа или теории групп) дает новый взгляд на перечислительные задачи и позволяет находить неожиданные подходы к их решению.

1.1 Перестановки и сочетания Будем обозначать число элементов в конечном множестве A через |A|; например, || = 3.

Пусть Nn обозначает множество натуральных чисел от 1 до n, т.е. Nn = . Перестановка этого множества это его взаимно-однозначное отображение в себя, : Nn Nn. Тождественная перестановка оставляет каждый элемент на месте. Множество всех перестановок этого множества обозначается через Sn. Композиция перестановок является перестановкой, и у каждой перестановки есть обратная такая, композиция с которой является тождественной перестановкой. Поэтому множество Sn образует группу.

Подсчитаем количество различных перестановок, т.е. количество элементов в группе Sn. Это количество равно количеству различных взаимнооднозначных отображений любых двух множеств из n элементов (не обязательно одинаковых). Подсчитать их можно, например, так. Группа S состоит, очевидно, из одного элемента тождественного отображения множества N1 = в себя. Разобьем теперь все взаимно-однозначные отображения из Nn в себя на n подмножеств в зависимости от того, в какой элемент перешел элемент 1. Все эти n подмножеств содержат одинаковое количество элементов, и это количество равно количеству взаимно-однозначных отображений двух (n 1)-элементных множеств, т.е. числу элементов группы Sn1. Поэтому Это число произведение всех натуральных чисел от 1 до n принято называть факториалом числа n и обозначать n!.

Множество Nn содержит n одноэлементных подмножеств. Нетрудно видеть, что число двухэлементных подмножеств в нем равно n(n1). Действительно, первый элемент из двух мы можем выбрать n способами, а второй n 1 способами из еще невыбранных элементов. Значит, упорядоченную пару элементов можно выбрать n(n 1) способами. Поскольку две пары a, b и b, a образуют одно и то же множество, для подсчета двухэлементных подмножеств необходимо количество упорядоченных пар поделить на 2.

Как подсчитать число k-элементных подмножеств в Nn для произвольного натурального числа k? Во-первых, очевидно, что при k n это число равно 0. Если же k n, то будем строить все k-элементные подмножества в Nn следующим образом. Возьмем произвольную перестановку множества Nn, и возьмем первые k элементов в этой перестановке (т.е. те элементы, в которые перешли 1, 2. k). Ясно, что таким образом мы получим все k-элементные подмножества, причем каждое из них будет встречаться одно и то же количество раз. Это количество раз равно k!(nk)!, поскольку перестановки первых k элементов и оставшихся n k элементов не меняют выбранное подмножество. Поэтому для подсчета числа k-элементных подмножеств в Nn нужно разделить общее число перестановок на k!(n k)!.

Полученное число называется числом сочетаний из n элементов по k и обозначается через (В литературе на русском и французском языках чаще встречается обознаk ло; мы же будем пользоваться сочетаниями в ситуациях, когда n не обязательно натуральное число, что и объясняет наш выбор обозначения n,k принятого в англоязычных текстах.) Поскольку дополнение k-элементного множества в множестве из n элементов состоит из n k элементов, количество k-элементных подмножеств в n-элементном множестве равно количеству (nk)-элементных подмножеств в нем, что прекрасно подтверждается выведенной нами формулой для числа сочетаний:

В случае k = n формула для числа сочетаний имеет вид Поскольку число n-элементных подмножеств в n-элементном множестве, очевидно, равно 1, мы обязаны положить 0! = 1. Тогда формула для числа сочетаний приобретает смысл и при k = 0:

в произвольном множестве имеется ровно одно 0-элементное подмножество (пустое множество).

Числа сочетаний это в точности коэффициенты, встречающиеся в разложении степеней бинома:

Действительно, и коэффициент при xnk y k в произведении равен количеству k-элементных подмножеств в множестве из n скобок (x + y). Это в точности те скобки, из которых мы выбираем слагаемое y.

Уже это простое наблюдение позволяет вывести нетривиальные комбинаторные тождества. Например, как результат подстановки x = 1, y = 1 в разложение бинома (1.2). (Вот другой вывод того же тождества: 2n это общее количество подмножеств в множестве из n элементов, а в левой части равенства суммируются количества подмножеств с данным числом элементов.) Точно так же получаем При нечетном n это равенство очевидным образом следует из симметрии k = nk, а вот при четном n его проще всего получить подстановкой x = 1, y = 1 в разложение бинома.

Разложение бинома нам еще не раз встретится в этой книге, в том числе и в настоящей главе.

1.2 Бином Ньютона Числитель и знаменатель дроби в формуле (1.1) для числа сочетаний можно сократить на (n k)!, переписав ее в виде Такое сокращение позволяет расширить круг значений, к которым она применима в качестве аргумента n можно брать произвольное число, не обязательно натуральное. Например, 1/2(1/2)(3/2)(5/2). ((3 2k)/2) При таком подходе число сочетаний перестает быть целым и теряет прямой комбинаторный смысл (нельзя сказать, что это число k-элементных подмножеств в “полуэлементном множестве”). Вообще, число n может быть иррациональным и даже комплексным. Однако по-прежнему естественно полагать для произвольного n = 0.

Если n натуральное или 0, то при k n в числителе формулы (1.3) встречается нулевой множитель, и поэтому все выражение равно 0. Напротив, если n не является целым неотрицательным числом, то число сочетаний k не является нулевым ни при каком k.

Такие обобщенные числа сочетаний можно применить для получения разложения бинома в произвольной степени, не только в целой. А именно, Здесь в обозначениях n заменено на, чтобы подчеркнуть, что мы больше не считаем показатель натуральным, а первая переменная заменена на 1, чтобы не было необходимости решать, что такое x в ненатуральной степени (1 = 1 для любого показателя ). В случае, если число является натуральным, разложение (1.4) совпадает с обычной степенью бинома. Для ненатурального показателя степени оно было введено Ньютоном и представляет собой бесконечный степенной ряд. Этот ряд можно считать определением левой части (а можно и в курсе математического анализа это делается доказывать, что ряд сходится при |s| 1, причем слева от знака равенства действительно написана функция, к которой он сходится).

Вот пример разложения бинома для = 1 :

1.3 Экспонента Экспонента является одной из важнейших функций во всей математике. Ее определяющее свойство состоит в том, что она преобразует сумму в произведение. Давайте найдем такую функцию f = f (s), что тождественно выполняется равенство Подставляя s = 0, t = 0, мы сразу заключаем, что f (0) = f (0) · f (0), откуда f (0) равняется либо 0, либо 1. Мы рассмотрим только случай f (0) = 1, оставив случай f (0) = 0 в качестве задачи в конце главы (см. задачу 1.4).

Пусть f имеет разложение Тогда условие (1.5) на функцию f записывается в виде равенства которое должно выполняться тождественно по s и t. Найдем, к каким ограничениям на коэффициенты ai приводит это равенство. Для этого будем последовательно сравнивать коэффициенты при мономах данной степени в левой и правой его частях. При мономах первой степени получаем равенство которое выполняется тождественно при любом значении коэффициента a1.

Зафиксируем какое-нибудь значение этого коэффициента и обозначим его через a, a1 = a.

Для мономов степени 2 должно выполняться равенство или которое выполняется тождественно только если a2 = a2 /2. Рассуждая так же далее получаем откуда Нетрудно видеть, что на каждом шаге, если соответствующее уравнение разрешимо, то решение единственно и дает значение an равным an с некоторым коэффициентом.

Можно было бы показать, что решение действительно всегда существует и коэффициент при an равен 1/n!. Мы поступим наоборот и определим экспоненту разложением Это бесконечный степенной ряд, коэффициенты которого обратные факториалы.

Теперь нетрудно проверить, что Действительно, нам надо доказать, что В левой части равенства моном sk tl появляется только в разложении бинома (s + t)n, где n = k + l, причем коэффициент при этом мономе равен Этот коэффициент в точности совпадает с коэффициентом при sk tl в правой части равенства. Поэтому всякий моном входит в левую и правую части равенства с одним и тем же коэффициентом.

Зная, что решение уравнения (1.5) с f (0) = 1 если оно существует однозначно определяется коэффициентом при s, мы заключаем, что экспонента и является этим единственным решением. При a = 0 экспонента тождественно равна 1. Если же a = 0, то экспонента eas получается из es обратимой заменой s на as. Поэтому чаще всего мы будем пользоваться экспонентой es, отвечающей значению a = 1.

Тригонометрические функции просто выражаются через экспоненту:

Здесь 1 комплексное число, квадрат которого равен 1; его часто обозначают через i, однако такое обозначение может привести к путанице.

Смысл переменной s, от которой берется экспонента, может быть самым разным. Например, s может обозначать дифференцирование:

и мы вправе спросить себя, что является экспонентой от дифференцироваdk ния. Здесь k-я степень дифференцирования dt это операция взятия k-ой производной, dt = dtk. Для того, чтобы понять, чему равна экспонента от дифференцирования, посмотрим, как она действует на многочленах.

Для этого достаточно посмотреть, как она действует на всех степенях tk переменной t. К счастью, результат (k + 1)-го и всех старших дифференd цирований монома tk равен 0, поэтому при применении e dt к tk в правой части равенства остается лишь конечное число слагаемых:

Правая часть последнего равенства есть не что иное как разложение бинома (1 + t)k, и мы заключаем, что Поскольку экспонента дифференцирования действует на многочленах линейно, это означает, что для любого многочлена p = p(t) Другими словами, экспонента дифференцирования является сдвигом на 1.

Это глубокое утверждение лежит в основе теории групп Ли. Мы будем им неоднократно пользоваться.

1.4 Производящие функции и действия над ними Перейдем к строгим определениям.

Определение 1.4.1. Пусть a0, a1, a2. произвольная (бесконечная) последовательность чисел. Производящей функцией (производящим рядом) для этой последовательности будем называть выражение вида или, в сокращенной записи, Если все члены последовательности, начиная с некоторого, равны нулю, то производящая функция является производящим многочленом.

Числа, входящие в последовательность, могут иметь различную природу. Мы будем рассматривать последовательности натуральных, целых, рациональных, вещественных и комплексных чисел. Производящую функцию, как и обычную функцию, мы будем часто обозначать одной буквой, указывая в скобках ее аргумент:

Две производящие функции равны в том и только в том случае, если у них совпадают коэффициенты при каждой степени переменной. Поэтому мы часто будем проверять равенство производящих функций или решать уравнения на них, последовательно сравнивая коэффициенты при s0, s1, s и т.д.

Замечание 1.4.2. Употребляя слово “функция”, мы вовсе не имеем в виду, что написанное выражение действительно является функцией. Так, не следует думать, будто мы можем сказать, чему равно “значение A(1) производящей функции A в точке 1”. Для этого нам пришлось бы сосчитать сумму бесконечного ряда a0 + a1 + a2 +. Изучение производящих функций не требует суммирования бесконечных числовых рядов. Переменная s является формальной, и сумма ряда a0 + a1 s + a2 s2 +. смысла не имеет.

Однако верны утверждения A(0) = a0, A (0) = a1, A (0) = 2a2 и т.д..

Производящая функция представляет последовательность чисел в виде ряда по степеням формальной переменной. Поэтому наряду с термином “производящая функция” мы будем также пользоваться термином “формальный степенной ряд”.

Определение 1.4.3. Суммой двух производящих функций называется производящая функция Произведением производящих функций A и B называется производящая функция Операции сложения и умножения производящих функций, очевидно, коммутативны (A + B = B + A, AB = BA) и ассоциативны ((A + B) + C = A + (B + C), (AB)C = A(BC)); кроме того, выполняется дистрибутивный закон (A(B + C) = AB + AC).

Определение 1.4.4. Пусть две производящие функции, причем B(0) = b0 = 0.

Подстановкой производящей функции B в производящую функцию A называется производящая функция A(B(t)) Если, например, B(t) = t, то Производящая функция A = A(s) называется четной, если A(s) = A(s) нечетной, если A(s) = A(s). Функция является четной в том и только в том случае, если ее степенной ряд содержит лишь члены четной степени.

Функция является нечетной в том и только в том случае, если ее степенной ряд содержит лишь члены нечетной степени. Так, например, функция cos(s) четная, функция sin(s) нечетная, а функция exp(s) не является ни четной, ни нечетной ее разложение в ряд содержит ненулевые коэффициенты как при четных, так и при нечетных степенях переменной s.

Обратите внимание на то, что операция подстановки функции, отличной от нуля в нуле, не определена. При попытке подставить такую функцию мы столкнулись бы с необходимостью суммировать бесконечные числовые ряды.

Конечно же, если обе производящие функции A и B являются многочленами, то определения суммы, произведения и подстановки для них совпадают с обычными определениями этих операций для многочленов. Определения этих операций на степенных рядах являются результатом их продолжения с многочленов.

Чтобы познакомиться с производящими функциями поближе, давайте докажем важную теорему. Линейную функцию B(t) = bt, b = 0, легко обратить обратной к ней относительно подстановки функцией является функция s/b. Добавление старших степеней переменной не влияет на обратимость функции.

Теорема 1.4.5 (об обратной функции). Пусть функция такова, что B(0) = b0 = 0, а b1 = 0. Тогда существуют такие функции что Функции A и C единственны.

Функция A называется левой обратной, а функция C правой обратной к функции B.

Доказательство. Докажем существование и единственность левой обратной функции. Доказательство для правой обратной аналогично. Будем определять коэффициенты функции A последовательно. Коэффициент a определяется из условия a1 b1 = 1, откуда Предположим теперь, что коэффициенты a1, a2. an уже определены. Коэффициент an+1 определяется из условия где точками обозначен некоторый многочлен от a1. an и b1. bn. Тем самым, условие представляет собой линейное уравнение на an+1, причем коэффициент bn+1 при an+1 отличен от нуля. Такое уравнение имеет единственное решение, и теорема доказана.

Итак, мы научились складывать и умножать степенные ряды и подставлять их друг в друга. Хотелось бы также научиться делить их друг на друга. Последняя операция не всегда корректно определена. В этом отношении степенные ряды похожи на целые числа: не всегда целое число при делении на другое целое число дает в ответе целое число. Однако, во всяком случае, возможно деление на степенной ряд, значение которого в нуле отлично от нуля.

Утверждение 1.4.6. Пусть формальный степенной ряд, причем A(0) = a0 = 0. Тогда существует единственный формальный степенной ряд такой что A(s)B(s) = 1.

Доказательство. Снова проведем доказательство по индукции. Значение коэффициента b0 находится легко, b0 = a0. Пусть теперь все коэффициенты ряда B вплоть до степени n1 однозначно определены. Коэффициент при sn определяется из условия Это линейное уравнение на bn, причем коэффициент a0 при bn отличен от нуля. Поэтому уравнение имеет единственное решение.

Отметим, что, несмотря на теоремы существования, нахождение обратной функции относительно подстановки или относительно деления в явном виде может оказаться сложной задачей, даже если сама функция относительно проста. Скажем, вычисление функции 1/ cos s займет у нас целый параграф, и приведет к очень интересному результату.

1.5 Дифференцирование и интегрирование производящих функций Для производящих функций обычное определение производной можно записать в следующем виде.

Определение 1.5.1. Пусть A = A(s) производящая функция. Производной этой функции называется функция Поскольку при t = 0 числитель дроби в определении производной обращается в нуль, этот числитель делится на t, и определение корректно.

Дифференцирование, очевидно, линейная операция, поэтому для того, чтобы понять, как оно действует на производящих функциях, достаточно посмотреть на его действие на степенях переменной. Имеем Здесь многоточие в числителе обозначает многочлен, делящийся на t2 ; после деления на t и приравнивания t нулю этот многочлен обращается в 0.

Тем самым, дифференцирование произвольной производящей функции A(s) = a0 + a1 s + a2 s2 +. дает Докажем правило дифференцирования сложной функции:

В силу линейности дифференцирования, для проверки этого равенства достаточно рассмотреть случай, когда A(s) = sk моном. Теперь мы должны доказать равенство для любой производящей функции B. Доказательство этого равенства требует последовательного сравнения коэффициентов при ti, i = 0, 1, 2.

Коэффициенты функции B при степенях i+2 и выше не влияют на коэффициенты при ti в обеих частях равенства. Поэтому его достаточно проверить для случая, когда B многочлен, а в этом случае оно хорошо известно.

Определение дифференцирования само по себе позволяет нам решать простейшие дифференциальные уравнения. Найдем, например, функцию, производная которой совпадает с ней самой, Пусть F имеет вид F (s) = f0 +f1 s+f2 s2 +. Тогда F (s) = f1 +2f2 s+3f3 s2 +. Сравнивая коэффициенты при нулевой степени переменной в левой и правой частях равенства (1.6), мы заключаем, что f1 = f0. Сравнение коэффициентов при первой степени s дает 2f2 = f1, откуда f2 = 2 f1 = 1 f0.

Продолжая таким же образом, мы заключаем, что fk = k! f0 для всех k = 1, 2, 3. Обозначим f0 через c. Наше рассуждение приводит к следующему выводу:

Всякое решение уравнения (1.6) имеет вид для некоторой постоянной c. Тем самым, уравнение (1.6) имеет единственное решение с заданным значением F (0) = c. Ниже в этой книге мы не раз будем обсуждать решение дифференциальных уравнений на производящие функции.

Интегралом функции A называется функция Операция дифференцирования обратна операции интегрирования:

Операция же интегрирования производной приводит к функции с нулевым свободным членом, и поэтому результат, вообще говоря, отличается от исходной функции, Замечание 1.5.2. Нетрудно видеть, что для функций, представимых в виде степенных рядов, формула для производной соответствует обычной. Формула для интеграла соответствует значению интеграла с переменным верхним пределом Последнее замечание позволяет подсчитывать производящие функции для большого числа разнообразных последовательностей. Вычислим, например, обратную функцию к экспоненте. Эта функция называется натуральным логарифмом и обозначается ln(·), ln(es ) = s. Разложение экспоненты начинается с 1, поэтому аргумент логарифма нужно сдвинуть в 1:

(свободный член в разложении равен 0, поскольку ln(1) = 0).

Для вычисления коэффициентов разложения логарифма воспользуемся тем, что производная функции и обратной к ней в произведении дают 1.

Действительно, если A(B(s)) = s, то A (B(s))B (s) = 1 и откуда, интегрируя, Мы будем чаще пользоваться следующим вариантом последней формулы:

Отметим, что бином Ньютона удобно записывать с помощью экспоненты:

В качестве еще одного примера, вычислим производящую функцию Умножая функцию f на s2 и дифференцируя, получаем откуда 1.6 Алгебра и топология формальных степенных рядов Ниже приводятся некоторые сведения из теории формальных степенных рядов.

Они не используются в книге, но могут помочь обозначить место этой теории в ряду других математических дисциплин.

С алгебраической точки зрения множество формальных степенных рядов (с коэффициентами в поле комплексных, вещественных или рациональных чисел) образует (бесконечномерное) векторное пространство над этим полем. Операция умножения рядов превращает это векторное пространство в алгебру, которая обозначается C[[s]] (соотв., R[[s]] или Q[[s]]). Важную роль в этой алгебре играют идеалы, т.е. такие подмножества I C[[s]], что f I I для любого элемента f C[[s]]. В алгебре формальных степенных рядов все идеалы главные, т.е. все они имеют вид f C[[s]] для некоторой функции f C[[s]]. Более того, все идеалы легко описать: они имеют вид Ik = sk C[[s]], k = 0, 1, 2. (т.е. идеал Ik состоит из всех формальных степенных рядов, делящихся на sk ). Эти идеалы вложены друг в друга, I1 I2 I3.

Один из идеалов Ik, а именно I1, максимален: он не содержится ни в каком другом идеале, отличном от всей алгебры. Алгебра с одним максимальным идеалом называется локальной. Свойство локальности сближает алгебру формальных степенных рядов с координатными алгебрами в окрестности начала координат (алгебрами ростков бесконечно дифференцируемых или аналитических функций).

Факторалгебры C[[s]]/Ik называются алгебрами срезанных многочленов и тоже очень важны.

В алгебре формальных степенных рядов определена топология. Открытыми в этой топологии являются идеалы Ik, k = 0, 1, 2. и пустое множество. Введенная топология определяет понятие сходимости: последовательность F1 (s), F2 (s).

сходится к формальному степенному ряду F (s), если для любого числа n существует такой номер N, что все коэффициенты при степенях s0, s1. sn у рядов Fk (s) при k N совпадают с коэффициентами при соответствующих степенях у ряда F (s). Многочлены формальные степенные ряды, в которых лишь конечное число коэффициентов отлично от нуля, образуют векторное подпространство (и подалгебру) в алгебре формальных степенных рядов, которое плотно относительно введенной топологии. Все операции над рядами сложение, умножение, подстановка, деление, определяются для многочленов обычным образом, а на степенные ряды продолжаются так, чтобы продолженные операции были непрерывны. Такие продолжения существуют и единственны.

Задача 1.1. Перестановка двух элементов множества Nn = , оставляющая остальные элементы на месте, называется транспозицией. Найдите число транспозиций в группе Sn.

Задача 1.2. Всякую перестановку можно разложить в произведение независимых циклов. Такое разложение однозначно с точностью до порядка умножаемых циклов. В частности, набор длин этих циклов определяется перестановкой однозначно. Например в Sn, для транспозиции набор длин циклов состоит из одной двойки и n 2 единиц, а набор длин циклов тождественной перестановки состоит из n единиц. Сумма длин циклов равна числу элементов перестановки; другими словами, набор этих длин является разбиением длины перестановки. Перестановка называется длинным циклом, если ее разложение в произведение независимых циклов состоит из единственного цикла. Длина такого цикла, разумеется, совпадает с длиной перестановки. Найдите число длинных циклов в группе Sn.

Задача 1.3. Найдите число элементов в Sn, отвечающих разбиениям а) 1n4 22 (произведение транспозиций двух пар элементов, среди которых нет общих); б) 1n3 31 (циклов длины 3).

Задача 1.4. Докажите, что если функция f = f (s), представимая в виде степенного ряда, преобразует сумму в произведение, т.е. тождественно выполняется равенство f (s + t) = f (s)f (t), и f (0) = 0, то она тождественно равна 0.

Задача 1.5. Докажите, что логарифм преобразует произведение в сумму:

Задача 1.6. Докажите следующие равенства: а) sin2 s + cos2 s = 1;

б) (1 + s) (1 + s) = (1 + s)+ ; в) ln((1 s) ) = ln(1 s).

Задача 1.7. Пусть p = p(t) многочлен. Чему равны а) exp(a dt )p(t)? б) sin dt p(t)? в) cos dt p(t)? г) exp( dt + dt2 )p(t)? д) exp( dt dt2 )p(t)?

Задача 1.8. Докажите, что степенные ряды вида образуют группу относительно операции подстановки.

Задача 1.9. Пусть функция B = B(s) = b1 s + b2 s2 + b3 s3 +. такова, что b1 = 0. Докажите, что правая обратная функция A(t) и левая обратная функция C(t) совпадают. Эта общая обратная функция обозначается через B 1 (t).

функции для последовательностей Задача 1.11. Вычислите три первых ненулевых коэффициента функций, обратных относительно операции подстановки к следующим функциям: а) sin s;

Задача 1.12. Найдите разложение арксинуса:

Задача 1.13. Докажите, что не существует такого формального степенного ряда A(s), что sA(s) = 1.

Задача 1.14. Докажите, что если каждый из степенных рядов A(s) и B(s) отличен от нуля, то и их произведение A(s)B(s) отлично от нуля.

Задача 1.15. Пусть ряды A(s) = a0 + a1 s + a2 s2 +. a0 = 0, и B(s) = b1 s+b2 s2 +. b1 = 0, имеют целые коэффициенты. При каких условиях на коэффициенты этих рядов ряды A(s), B 1 (s) имеют целые коэффициенты?

Задача 1.16. Найдите все решения дифференциальных уравнений а) F (s) = aF (s), б) F (s) = F 2 (s).

Задача 1.17. Найдите производящие функции для последовательностей Задача 1.18. Докажите, что для ряда B = B(t) с нулевым свободным членом, B(0) = 0, и произвольного ряда A = A(s) (формула замены переменных в интеграле).

Задача 1.19. Докажите формулу Ньютона–Лейбница Задача 1.20. Докажите формулу интегрирования по частям:

Задача 1.21. Докажите, что при заданном натуральном значении k любое натуральное число n единственным образом представимо в виде где 0 b1 b2 · · · bk. Например, при k = 1 это верно, так как всякое число n допускает единственное представление в виде n = n. Нижеследующие задачи взяты из знаменитого сборника Полиа и Сеге “Теоремы и задачи из анализа” в скобках указан номер задачи в этом сборнике.

Задача 1.22 (I.16). Определите коэффициент an в разложении Задача 1.23 (I.33). Докажите тождество Задача 1.24 (I.37). Докажите тождество Задача 1.25 (I.38). Докажите тождество Задача 1.26 (I.39). Докажите тождество Задача 1.27 (I.41). Положим Докажите, что тогда (Обратите внимание на то, что функции и, хотя и представляют собой бесконечные суммы, не являются формальными степенными рядами, а значения (n) и (n) при натуральном аргументе n корректно определены, поскольку при подстановке в ряды натурального значения аргумента все слагаемые кроме конечного числа обращаются 0.) Задача 1.28 (I.42). Докажите тождество Задача 1.29 (I.44). Докажите, что для любого многочлена f выполняется равенство Глава Рациональные производящие функции Рациональная функция это отношение двух многочленов. Рациональные производящие функции образуют большой класс производящих функций.

Производящие функции, встречающиеся на практике, очень часто принадлежат к этому классу. Например, как мы увидим, рациональными оказываются производящие функции для языков, распознаваемых конечными автоматами (регулярных языков, см. главу 12). Кроме того, теория рациональных производящих функций совпадает, по существу, с теорией решений обыкновенных дифференциальных уравнений с постоянными коэффициентами.

2.1 Геометрическая прогрессия Простейшая рациональная функция отвечает простейшей последовательности коэффициентов постоянной последовательности 1, 1, 1. Производящая функция для этой последовательности имеет вид и ее несложно выразить через элементарные производящие функции, которые мы рассматривали в предыдущей главе. Действительно, умножив обе части равенства (2.1) на s, получим откуда Тот же вывод с незначительными изменениями проходит для произвольной последовательности вида a, ar, ar2, ar3. :

откуда Приведенные выше выкладки представляют собой не что иное, как известный вывод формулы для суммы бесконечной геометрической прогрессии. Результат этих выкладок согласуется, как нетрудно видеть, с разложением бинома (1 s)1.

2.2 Последовательность Фибоначчи Знаменитая последовательность Фибоначчи определяется своими начальными членами f0 = f1 = 1 и соотношением Из этого соотношения легко получить начало последовательности Фибоначчи в которой каждый член, начиная с f2, равен сумме двух предыдущих. Чтобы вывести формулу производящей функции умножим обе части равенства (2.5) на s + s2. Получим или откуда Полученную формулу можно понимать как композицию двух производящих функций, а именно, (1 s)1 и s + s2, т.е.

Такое разложение, однако, не очень удобно, так как в его членах перемешаны различные степени переменной s и оно не дает явной формулы для коэффициентов. Полезнее представить дробь в виде суммы двух элементарных дробей:

где s1 = (1 + 5)/2, s2 = (1 5)/2 корни уравнения 1 s s2 = 0.

Из последнего разложения немедленно получаем Поэтому Здесь мы воспользовались тем, что s1 s2 = 1.

Число |1/s1 | = |s2 | = 1+2 5 1.6180339887 называется золотым сечением. Прямоугольник, отношение сторон которого равно золотому сечению, можно разрезать на два подобных ему одинаковых прямоугольника.

Другой способ вывода производящей функции для чисел Фибоначчи использует элементарные понятия линейной алгебры. Рассмотрим пару последовательных чисел Фибоначчи fn, fn+1 как координаты вектора в двумерном вещественном пространстве R2 :

Тогда соотношение (2.4) можно интерпретировать как правило перехода от вектора fn+1 к вектору fn+1 :

Последнее преобразование линейно, и его можно записать в матричном виде:

Переход от вектора fn+2 к вектору fn+3 осуществляется путем повторного применения преобразования, и т.д. Таким образом, производящая функция для векторной последовательности Фибоначчи принимает вид Здесь через I обозначена единичная матрица, I =, и мы применили к векторной производящей функции вывод производящей функции для геометрической прогрессии. Единственное отличие в результате: выражение (I s)1 понимается как обратная матрица к матрице I s.

Явное выражение для чисел Фибоначчи можно получить, вычислив явно матрицу n для произвольного n. Для этого матрицу нужно диагонализировать, представив ее в виде где диагональная матрица, а матрица L невырождена. Имеем, Отсюда, воспользовавшись соотношением и выражениями для чисел s1, s2, получаем равенство (2.7).

2.3 Рекуррентные соотношения и рациональные производящие функции Последовательность Фибоначчи определяется линейным рекуррентным соотношением fn+2 = fn+1 + fn. Исходя из этого соотношения и начальных значений последовательности, мы смогли найти явный вид производящей функции. Производящая функция оказалась рациональной отношением двух многочленов. На самом деле в нашем выводе нигде не использовался конкретный вид рекуррентного соотношения. Действуя точно таким же образом, мы можем доказать аналогичную теорему о производящей функции для произвольной последовательности, задаваемой линейным рекуррентным соотношением.

Теорема 2.3.1. Пусть последовательность an задается линейным рекуррентным соотношением порядка k с постоянными c1. ck :

и числа a0, a1. ak1 заданы. Тогда производящая функция A(s) = a0 + a1 s + a2 s2 +. рациональна, A(s) = Q(s), причем степень многочлена Q равна k, а степень многочлена P не превосходит k 1.

Доказательство. Доказательство этой теоремы повторяет, по существу, рассуждение для чисел Фибоначчи. Умножив производящую функцию A(s) на c1 s + c2 s2 + · · · + ck sk, получим некоторый многочлен, степень которого не превосходит k 1. Дейгде P ствительно, коэффициент при sn+k в правой части первого равенства совпадает с правой частью выражения (2.8). Отсюда непосредственно получаем утверждение теоремы.

Отметим, что в процессе доказательства теоремы 2.3.1 был выписан явный вид многочлена Q, стоящего в знаменателе рациональной производящей функции:

Этот многочлен определяется рекуррентным соотношением, а для вычисления числителя функции нам необходимо знать начальные члены последовательности.

Производящая функция для чисел Фибоначчи представима в виде линейной комбинации двух дробей 1/(1 s/s1 ) и 1/(1 s/s2 ). Нетрудно видеть, что аналогичное утверждение справедливо и для любой рациональной функции:

Теорема 2.3.2. Пусть F (s) = P (s)/Q(s) представление рациональной производящей функции в виде отношения двух взаимнопростых многочленов, Q(0) = 1. Тогда F представляется в виде суммы многочлена и линейной комбинации элементарных дробей вида 1/(1 qi s)ki, где значения qi обратны (комплексным) корням многочлена Q, а показатели степени ki не превосходят кратности корня 1/qi. Такое представление единственно.

Действительно, пусть d1. dm кратности попарно различных комплексных корней многочлена Q, а q1. qm величины, обратные к этим корням. Представим многочлен Q в виде произведения где каждый из многочленов Qi (s) имеет единственный корень 1/qi, Qi (s) = (1qi s)di. Существует константа cm, такая, что знаменатель разности F (s) cm /(1 qm s)dm имеет степень, меньшую чем Q. Эта константа равна значению рациональной функции в точке s = 1/qm. Теперь теорема доказывается индукцией по степени знаменателя.

Вывод векторной производящей функции для последовательности Фибоначчи также непосредственно переносится на случай произвольной рекуррентной последовательности. В общем случае двумерный вектор следует заменить k-мерным вектором а матрица A перехода к следующему k-мерному вектору, соответствующая рекуррентному соотношению, будет выглядеть так:

Таким образом, мы получаем векторную производящую функцию Матрица, задающая рекуррентное соотношение для чисел Фибоначчи, приводится к диагональному виду линейным преобразованием. Для произвольной матрицы A это, вообще говоря, не так. Это можно сделать, лишь если ее собственные числа попарно различны. Однако в общем случае ее можно привести к жордановой нормальной форме, степени которой также несложно вычислить.

Оказывается, рациональные производящие функции в точности совпадают с производящими функциями для последовательностей, задаваемых линейными рекуррентными соотношениями. Точнее, справедлива следующая обратная теорема.

Теорема 2.3.3. Если производящая функция A(s) = a0 +a1 s+a2 s2 +. раP (s) циональна, A(s) = Q(s), где многочлены P и Q взаимно просты, Q(0) = 0, то начиная с некоторого номера n последовательность a0, a1, a2. задается линейным рекуррентным соотношением где k степень многочлена Q, а c1, c2. ck некоторые константы.

Доказательство читателю предлагается провести самостоятельно.

2.4 Неоднородные рекуррентные соотношения В предыдущем параграфе мы построили рациональные производящей функции для последовательностей, заданных линейными рекуррентными соотношениями с постоянным коэффициентами. Эти соотношения линейны и однородны каждое слагаемое в правой их части представляет собой член последовательности, умноженный на некоторую константу. Наше построение несложно обобщить на случай неоднородных соотношений. Рассмотрим последовательность 2, 3, 5, 9, 17. заданную соотношением с начальным условием a0 = 2. Это рекуррентное соотношение порядка очередной член последовательности определяется предыдущим членом.

Однако в отличие от рекуррентных соотношений, рассматривавшихся нами ранее, в правой части соотношения (2.10) имеется неоднородная добавка константа 1. Как следствие, теорема 2.3.1 напрямую неприменима.

Для того, чтобы вычислить производящую функцию выпишем рекуррентное соотношение (2.10) для члена проследовательности с номером n + и, вычтя из него исходное соотношение, получим В результате мы свели соотношение первого порядка (2.10) к линейному рекуррентному соотношению второго порядка, а такие соотношения мы уже умеем решать.

Ясно, как обобщить это рассуждение на случай рекуррентного соотношения произвольного порядка, в котором добавка представляет собой произвольный многочлен.

Теорема 2.4.1. Пусть последовательность a0, a1. задана линейным неоднородным рекуррентным соотношением с постоянными коэффициентами порядка k, т.е. an+k = c1 an+k1 + c2 an+k2 + · · · + ck an + hm (n), где hm (n) есть многочлен степени m от номера n члена последовательности.

Тогда последовательность an задается однородным линейным рекуррентным соотношением порядка n + m + 1 с постоянными коэффициентами и, как следствие, производящая функция A(s) для нее рациональна.

Доказательство. Пусть многочлен hm имеет вид Член последовательности с номером n + k + 1 имеет вид Разность этого и предыдущего членов равна an+k+1 an+k = c1 an+k + (c2 c1 )an+k1 + · · · ck an + (hm (n + 1) hm (n)).

Тем самым, мы представили член последовательности с номером n + k + 1 в виде линейной комбинации предыдущих k + 1 членов последовательности, к которой прибавлен многочлен hm (n + 1) hm (n). Этот многочлен имеет вид т.е. коэффициент при nm в нем равен 0 и его степень как многочлена от n меньше m. Теперь мы можем рассуждать по индукции, последовательно уменьшая степень многочлена h в правой части рекуррентного соотношения, пока она не станет равной 0 случай, обращаться с которым мы уже научились.

2.5 Произведение Адамара рациональных производящих функций Одно из наиболее привлекательных свойств рациональных производящих функций их замкнутость относительно произведения Адамара.

Определение 2.5.1. Произведением Адамара производящих функций называется производящая функция Таким образом, произведение Адамара двух последовательностей это последовательность, состоящая из почленных произведений соответственных членов этих последовательностей. Необходимость в производящей функции для произведения Адамара возникает при перечислении пар объектов одинакового порядка: если число объектов первого типа равно an, а число объектов второго типа bn, то число пар объектов, составленных из элементов первого и второго типа, равно an bn.

Теорема 2.5.2. Произведение Адамара двух рациональных производящих функций рационально.

Для доказательства этой теоремы нам понадобится новая характеризация рациональных производящих функций.

Лемма 2.5.3. Производящая функция для последовательности a0, a1, a2. рациональна тогда и только тогда, когда существуют такие числа q1. ql и такие многочлены p1 (n). pl (n), что Выражение в правой части равенства (2.11) называется квазимногочленом от переменной n.

Доказательство. Заметим прежде всего, что производящая функция (1 qs)k имеет вид Коэффициент при sn в этой производящей функции равен где Pk1 (n) = (n + 1)(n + 2). (n + k 1) многочлен от n степени k 1. Всякая рациональная функция от переменной s представляется в виде суммы многочлена и линейной комбинации элементарных дробей вида ( qi s)ki, поэтому коэффициенты соответствующей производящей функции являются квазимногочленами.

Наоборот, предположим, что коэффициенты производящей функции, начиная с некоторого номера, представляются в виде квазимногочлена. Покажем, что в случае квазимногочлена p(n)q n соответствующая производящая функция рациональна. Пусть степень многочлена p равна k 1. Многочлены P0, P1. Pk1, определенные равенством (2.12), образуют базис в пространстве многочленов степени не выше k 1. И в самом деле, любая последовательность многочленов степеней 0, 1. k 1 образует базис в этом пространстве. Поэтому многочлен p представляется в виде линейной комбинации многочленов Pi и соответствующая производящая функция есть просто линейная комбинация функций (1qs)j, j = 0, 1. k 1.

Для произвольного квазимногочлена мы получаем линейную комбинацию функций такого вида при разных qi. Лемма доказана.

Доказательство теоремы 2.5.2. Для завершения доказательства теоремы осталось заметить, что произведение квазимногочленов является квазимногочленом. Это утверждение непосредственно вытекает из формулы (2.11).

2.6 Асимптотика коэффициентов рациональных При решении перечислительных задач зачастую приходится интересоваться поведением числа элементов множества при росте перечисляющего параметра. Это особенно важно, если мы хотим, например, перечислять объекты на компьютере и пытаемся оценить время работы программы.

Определение 2.6.1. Функции f : N R и g : N R имеют одинаковую асимптотику, или одинаковый рост, при n, если существует предел limn f (n) и он равен 1. Функция f растет медленнее функции g, если предел limn f (n) существует и он равен 0. В последнем случае говорят также, что функция g растет быстрее функции f.

При вычислении асимптотики некоторые функции мы считаем “образцами”, а другие “сводим” к этим образцам. В качестве образцов берутся обычно наиболее простые монотонные функции, поведение которых хорошо изучено. Образцами могут служить • экспонента an при различных значениях основания a 0;

• степенная функция n при различных значениях показателя ;

а также произведения и композиции этих функций в различных комбинациях.

Нетрудно расположить функции-образцы в порядке убывания скорости роста:

Пример 2.6.2. Коэффициенты производящей функции ln(1 s)1 = s + 2 s + 3 s +. растут, как n (в этом случае естественнее было бы говорить “убывают, как n ”).

Пример 2.6.3. Асимптотика произвольного многочлена p(n) = c0 nk +c1 nk1 + · · · + cn, c0 0, совпадает с асимптотикой его старшего члена c0 nk.

В этом разделе мы найдем асимптотику коэффициентов рациональных производящих функций. Согласно лемме 2.5.3, последовательность коэффициентов рациональной производящей функции, начиная с некоторого момента, является квазимногочленом (2.11), в котором q1. ql некоn торые комплексные числа. Если |qi | |qj |, то последовательность pi (n)qi растет медленнее, чем pj (n)qj какими бы ни были ненулевые многочлены pi (n) и pj (n). Действительно, отношение этих последовательностей стремится к нулю, поскольку qj 1, и n-я степень этого числа стремится к нулю быстрее любой заданной степени числа n. Тем самым, асимптотика квазимногочлена (2.11) определяется слагаемыми, содержащими qi с самыми большими модулями.

В свою очередь, асимптотика многочлена p(n)q n определяется старшим мономом многочлена p, поэтому асимптотика любого слагаемого pi (n)qi в квазимногочлене совпадает с асимптотикой монома ci n qi, где ci n старший моном многочлена pi. Тем самым, мы приходим к следующему утверждению.

Утверждение 2.6.4. Если в квазимногочлене (2.11) имеется единственn ное слагаемое pi (n)qi с наибольшим по модулю значением qi и многочленом pi наибольшей степени, то асимптотика этого квазимногочлена совпадает с асимптотикой монома |ci |ndi |qi |n, где ci ndi старший моном многочлена pi.

Если же таких слагаемых несколько, то вопрос об асимптотике становится более тонким. Например, в последовательности, задаваемой квазимногочленом (2)n + 2n (отвечающим значениям q1 = 2, q2 = 2, deg p1 = deg p2 = 0), все члены с нечетными номерами равны 0, в то время, как члены с четными номерами n = 2k растут как 2 · 22k. Поэтому вопрос об асимптотике таких квазимногочленов требует более аккуратной постановки и более тщательного исследования.

Приведенный пример показывает, что при наличии нескольких значений qi с наибольшим модулем, степени многочленов при которых совпадают, разные подпоследовательности значений многочлена имеют различную асимптотику. Поэтому речь может идти только об асимптотике “наиболее возрастающих” подпоследовательностей. Это те подпоследовательности, в которых модули слагаемых суммируются (или почти суммируются).

Для таких подпоследовательностей утверждение 2.6.4 принимает следующий вид.

Утверждение 2.6.5. Если в квазимногочлене (2.11) имеется несколько слагаемых pi (n)qi с наибольшим по модулю значением qi и многочленом pi наибольшей степени d, то последовательность значений этого квазимногочлена содержит подпоследовательность, асимптотика которой совпадает с асимптотикой монома cnd |q|n, где c = |ci | сумма модулей старших коэффициентов многочленов pi, d общее значение модулей чисел qi. Это наибольшая возможная асимптотика подпоследовательности значений квазимногочлена.

Доказательство этого утверждения аналогично доказательству утверждения 2.6.4, и мы его не приводим.

Для квазимногочлена (2.11), отвечающего рациональной функции Q(s), постоянные qi это величины, обратные к корням многочлена Q, т.е. к полюсам рациональной функции. В свою очередь, степень многочлена pi это уменьшенный на 1 порядок полюса функции Q(s) в точке s = 1/qi. Поэтому утверждение 2.6.4 можно переформулировать следующим образом.

Утверждение 2.6.6. Если у рациональной функции Q(s) среди ближайших к началу координат полюсов имеется единственный полюс 1/q наибольшего порядка k, то асимптотика ее коэффициентов совпадает с асимптотикой коэффициентов элементарной дроби c/(1 qs)k в разложении этой функции в сумму элементарных дробей.

Утверждение 2.6.5 допускает аналогичную переформулировку.

В частности, для рациональной функции, задаваемой рекуррентным соотношением (2.8), асимптотика ее коэффициентов определяется ближайшими к началу координат корнями многочлена Q(s) = 1 c1 s c2 s2 · · · ck sk и их порядками. Например, для последовательности Фибоначчи Q(s) = 1 s s2, поэтому ближайший к началу координат корень вещественный, равен s1 = (1 + 5)/2 и имеет порядок 1. Значит, числа Фибоначчи имеют асимптотику c(1/s1 )n для некоторой константы c. Мы вычислили эту константу она оказалась равна (1 + 5)/2 5.

Задача 2.1. Рекуррентное правило образования последовательности Фибоначчи позволяет продолжить ее “назад” для отрицательных значений индекса. Так, например, f1 = 0. Чему равно f10 ?

Задача 2.2. Рациональны ли производящие функции для последовательностей Найдите соответствующие производящие функции в тех случаях, когда они рациональны.

Задача 2.3. Найдите представление в виде суммы элементарных дробей слеs 1+2s дующих рациональных функций: а) 1s2s2 ; б) 13s+4s3 ; в) 13s3.

Задача 2.4. Найдите представление в виде квазимногочлена и линейные рекуррентные соотношения с постоянными коэффициентами для коэффиs 1+2s циентов следующих степенных рядов: а) 1s2s2 ; б) 13s+4s3 ; в) 13s3.

Задача 2.5. Известно, что следующие последовательности задаются линейными рекуррентными соотношениями с постоянными коэффициентами порядка 3: а) 1, 2, 6, 18, 52, 152, 444. ; б) 1, 2, 2, 6, 8, 16, 28, 48, 88. в) 1, 2, 3, 6, 9, 18, 27. Найдите эти соотношения и проверьте, что выписанное начало последовательности действительно им подчиняется.

Задача 2.6. Найдите производящие функции и линейные рекуррентнные соотношения с постоянными коэффициентами для следующих последовательностей, заданных квазимногочленами: а) an = 2 · 3n 3 · 2n ; б) bn = Задача 2.7. Пользуясь производящей функцией для чисел Фибоначчи, докажите для них тождества Задача 2.8. Докажите теорему 2.3.3.

Задача 2.9. Докажите, что в жордановой нормальной форме матрицы из уравнения (2.9) каждому собственному числу соответствует одна жорданова клетка, размер которой равен кратности этого собственного числа как корня характеристического многочлена. [Указание: Воспользуйтесь связью между кратностью собственного числа и порядком нуля многочлена в знаменателе рациональной производящей функции.] Задача 2.10. Найдите производящие функции и явные выражения для элементов последовательностей, заданных рекуррентными формулами:

а) an+2 = 4an+1 4an, a0 = a1 = 1;

б) an+3 = 3an+2 3an+1 an, a0 = 1, a1 = a2 = 0;

в) an+3 = 2 an+2 1 an, a0 = 0, a1 = 1, a2 = 2.

Задача 2.11. Найдите производящую функцию для чисел Фибоначчи с четными номерами n f2n sn.

Задача 2.12. Найдите производящую функцию для последовательности 2, 3, 5, 9, 17. заданную неоднородным линейным рекуррентным соотношением an+1 = 2an 1.

Задача 2.13. Для следующих последовательностей, заданных неоднородными линейными рекуррентными соотношениями, найдите задающие их однородные линейные рекуррентные соотношения и производящие функции: а) an+1 = an + 2, a0 = 1; б) an+2 = an + n + 1, a0 = 1, a1 = 0; в) an+2 = an+1 an + n2 + 1, a0 = 1, a1 = 0.

Задача 2.14. Найдите произведения Адамара функций от s Задача 2.15. Найдите производящие функции для последовательностей, заданных рекуррентными соотношениями а) Jn = Jn1 +2Jn2 (1, 1, 3, 5, 11. );

б) Tn = Tn1 + Tn2 + Tn3 (1, 1, 2, 4, 7. “числа Трибоначчи”).

Задача 2.16. Докажите, что производящая функция ln(1 s) не является рациональной а) воспользовавшись известной асимптотикой ее коэффициентов; б) воспользовавшись тем, что знаменатель ее производной 1/(1 s) имеет в точке s = 1 нуль кратности 1.

Задача 2.17. Докажите, что производящая функция, обратная к функции G(s) = s + s2 (т.е. функция, выражающая s через t = G(s)), не является рациональной.

Задача 2.18. Найдите произведение Адамара Задача 2.19. Докажите, что множество формальных степенных рядов, все коэффициенты которых отличны от 0, образует группу относительно произведения Адамара.

Задача 2.20. Обозначим через an число разбиений полоски шириной 1 и длиной n квадратиков на части, каждая из которых является либо квадратиком 1 1, либо домино 1 2. Например, a1 = 1, a2 = 2, a3 = 3, a4 = 5.

Найдите производящую функцию для последовательности an.

Задача 2.21. Обозначим через bn число разбиений полоски шириной 2 и длиной n квадратиков на домино 1 2. Например, b0 = 1, b1 = 1, b2 = 2, b3 = 3. Найдите производящую функцию для последовательности bn.

Задача 2.22. Обозначим через cn число разбиений полоски шириной 3 и длиной n квадратиков на домино 1 2. Например, c0 = 1, c1 = 0, c2 = 3, c3 = 0. Найдите производящую функцию для последовательности cn.

Задача 2.23. Обозначим через dn число разбиений стоимости n полоски шириной 2 и длиной несколько квадратиков на домино 1 2. Здесь стоимость замощения равна h + 2v, где h количество горизонтальных, а v количество вертикальных доминошек в замощении. Например, d0 = 1, d1 = 0, d2 = 2, d3 = 0, d4 = 4. Найдите производящую функцию для последовательности Задача 2.24. Обозначим через tn число разбиений полоски шириной 1 и длиной n квадратиков на части, каждая из которых является либо квадратиком 1 1, либо домино 1 2, либо тримино 1 3. Например, t1 = 1, t2 = 2, t3 = 4, t4 = 7. Найдите производящую функцию для последовательности Задача 2.25. Найдите производящую функцию для количества лесенок площадью n клеток на клетчатой плоскости (см. Рис. 2.1), состоящих из не более, чем а) двух ступенек; б) трех ступенек. (Высота каждой ступеньки равна 1, и при движении снизу вверх ступеньки укорачиваются.) Рис. 2.1: Лесенка из трех ступенек, состоящая из 10 клеток Задача 2.26. Преобразованием Пфаффа последовательности , n = 1, 2. называется последовательность pn = Pf(), состоящая из пфаффианов (пфаффиан кососимметрической матрицы равен квадратному корню из ее определителя). Например, первые члены преобразования Пфаффа последовательности степеней двойки 1, 2, 4. 2n1. равны Докажите, что преобразование Пфаффа переводит а) последовательность в последовательность единиц 1, 1, 1. ; б) последовательность в последовательность единиц 1, 1, 1. ; в) последовательность Фибоначчи Fibn в последовательность степеней двойки 1, 2, 4. 2n1.

Найдите преобразование Пфаффа последовательностей г) Jn и д) Tn из задачи 2.15.

Задача 2.27. Полимино это область на клетчатой плоскости, ограниченная простой замкнутой ломаной, идущей по сторонам клеток. (Два полимино одинаковы, если одно можно получить из другого сдвигом.) Полимино называется стековым, если нижние горизонтальные отрезки его границы образуют один отрезок (см. рис. 2.2). Докажите, что число стековых полимино с периметром 2n + 2 равно Fib2n2. На рис. 2.3 изображены все стековых полимино с периметром 8 (n = 3).

Задача 2.28. (Фибоначчиева система счисления) Докажите, что любое натуральное число единственным образом представляется в виде a1 f1 +a2 f2 +. где fn числа Фибоначчи, а каждое из чисел ai равно нулю или единице, причем единиц в сумме конечное число и два идущих подряд элемента последовательности ai не могут равняться единице. Придумайте алгоритмы перевода чисел из фибоначчиевой системы счисления в позиционную и обратно, а также алгоритмы сложения и умножения чисел в этой системе счисления.

Задача 2.29. Пусть рациональные производящие функции, заданные несократимыми дробями, их произведение Адамара, представленное в виде несократимой дроби. Что можно сказать про многочлен Q, если многочлены Q1 и Q2 известны?

Задача 2.30. Сколько цифр в десятичной записи числа Фибоначчи с номером а) 100; б) 1000?

Задача 2.31. Какую наибольшую асимптотику может иметь подпоследовательность последовательности коэффициентов производящей функции Глава Перечисление путей на графах Многие последовательности натуральных чисел полезно представлять себе как последовательности, перечисляющие пути в некоторых графах. При этом вид графа оказывается тесно связан со свойствами производящих функций, отвечающих данным последовательностям. Задачи о перечислении путей часто встречаются в статистических моделях математической физики. В этой главе мы рассмотрим примеры таких перечислений.

3.1 Пути в графах Граф представляет из себя набор вершин, некоторые из которых соединены ребрами. Часто удобно представлять себе граф нарисованным на плоскости (см. рис. 3.1). Среди перечислительных задач, о которых мы будем говорить, есть задачи перечисления путей в графе. Например, сосчитаем количество различных путей ладьи из клетки A в клетку B на доске, изображенной на рис. 3.2 а), при условии, что ладья может ходить только вправо или вверх в клетку, соседнюю с той, в которой она находится.

Такие задачи проще всего решаются следующим способом. Поставим 1 в каждую клетку, до которой из A можно дойти за один шаг. Затем поставим числа во все клетки, до которых можно дойти за один шаг из этих клеток.

Эти числа равны суммам всех единиц в клетках, из которых можно попасть в эти. Этот процесс можно продолжить и дальше, пока мы не доберемся до Рис. 3.2: а) Шахматная доска с вырезом и б) подсчет количества путей ладьи, ведущих из клетки A в клетку B; в каждой клетке указано количество путей из A в эту клетку клетки B, см. рис. 3.2 б). Число 100 сумма чисел в соседних клетках слева и снизу, которое должно стоять в этой клетке, и будет интересующим нас количеством различных путей. Разнообразные варианты этого простого рассуждения играют принципиальную роль в решении многочисленных задач.

3.2 Пути, перечисляемые рациональными производящими функциями Построим граф, пути в котором перечисляются последовательностью Фибоначчи. Мы рассмотрим два варианта построения такого графа. В первом варианте расположим (бесконечное) множество вершин графа слева направо и будем считать вершины занумерованными числами 0, 1, 2, 3. Соединим каждую вершину ребром с ее правым соседом, а также с вершиной, следующей за ее правым соседом (см. рис. 3.3). (Мы делаем исключение, не проводя горизонтальную стрелку из первой вершины во вторую начальные значения последовательности Фибоначчи заданы и не подчиняются рекуррентному правилу.) На каждом ребре поставим стрелку, указывающую направление движения по нему. Для каждой вершины графа подсчитаем различные пути, идущие из двух начальных вершин в данную. Ясно, что число различных путей, ведущих из начальных вершин в вершину с номером n + 1, n 1, равно сумме числа путей, ведущих в вершину с номером n 1, и числа путей, ведущих в вершину с номером n. Тем самым, числа путей удовлетворяют тому же рекуррентному соотношению, что и числа Фибоначчи, и тем же начальным условиям; поэтому последовательность этих чисел совпадает с последовательностью Фибоначчи.

Другой способ построения графа состоит в следующем. Нарисуем вместо одной две бесконечные последовательности вершин, одна над другой.

Для удобства мы верхнюю последовательность сдвинем на одну позицию вправо (см. рис. 3.4). Из каждой вершины нижнего ряда выходят стрелки в Рис. 3.3: Бесконечный граф для изображения путей, перечисляемых числами Фибоначчи соседние с ней справа вершины обоих рядов. Из каждой вершины верхнего ряда выходит стрелка в соседнюю справа вершину нижнего ряда. Число путей в этом графе, идущих из начальной точки в точку с номером n в нижнем ряду точек, равно n-ому числу Фибоначчи. Над ним стоит (n 1)-е число Фибоначчи. Пару чисел в графе, стоящих одно над другим, можно рассматривать как координаты двумерного вектора. Тогда преобразование перехода от очередной пары точек, образующих вертикальный столбец, к следующей паре есть не что иное как линейное преобразование, которое мы рассматривали в п. 2.2: верхнее число в новом столбце совпадает с нижним числом предыдущего столбца, а нижнее равно сумме верхнего и нижнего чисел из предыдущего столбца.

B 1 rB 1 rB 2 rB 3 rB 5 rB 8 rB13r21r34r

Видео:Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать

E E E B B B

Рис. 3.4: Бесконечный граф из двух рядов вершин для изображения путей, перечисляемых числами Фибоначчи Обобщим нашу конструкцию с чисел Фибоначчи на произвольные рациональные производящие функции. Обобщению поддаются оба способа построения графа, однако мы будем говорить лишь о втором, который приводит к “более читаемым” картинкам. Согласно теореме 2.3.1, последовательность коэффициентов рациональной функции задается линейным рекуррентным соотношением с постоянными коэффициентами вида (2.8). В качестве примера рассмотрим последовательность, задаваемую соотношением третьего порядка с начальными условиями a0 = 1, a1 = 0, a2 = 2. Вот начало этой последовательности: 1, 0, 2, 5, 10, 22. Поскольку порядок рекурентного соотношения равен 3, вершины графа образуют три последовательности (см.

рис. 3.5). Из каждой вершины двух нижних рядов идет стрелка в вершину следующего ряда, стоящую в следующем столбике. Кроме того, из каждой вершины третьего ряда и из каждой вершины нижнего ряда, начиная с третьей, идет стрелка в вершину нижнего ряда, стоящую в следующем столбике. При этом над горизонтальными стрелками в первом ряду мы ставим число 2 “кратность”, или “вес отрезка пути”. Вместо этого мы могли бы нарисовать две стрелки, однако это загромоздило бы рисунок (загромождение было бы еще более заметно, если бы вместо коэффициента 2 стояло большее число). Точно так же мы могли бы нарисовать стрелки из второго ряда в нижний, поставив на них кратность 0, что тоже не сделало бы рисунок прозрачней.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

B B B B B B B B

Рис. 3.5: Бесконечный граф для изображения путей, перечисляемых коэффициентами рациональной функции Теперь ясно, как нарисовать граф, отвечающий произвольной рациональной функции. Кратность ребра при этом может быть произвольным числом, не обязательно натуральным (например, кратность может быть дробной или отрицательной). Эта кратность равна соответствующему коэффициенту в рекуррентном соотношении, задающем коэффициенты разложения рациональной функции. С помощью подобного графа легко сосчитать первые члены последовательности. Такой способ подсчета может оказаться эффективнее вычислений с помощью квазимногочленов в том случае, если нули знаменателя рациональной функции не рациональны.

3.3 Числа Каталана Порядок вычислений в арифметических выражениях задается расстановкой скобок, например, Если стереть все элементы выражения, за исключением скобок, то оставшиеся скобки образуют правильную скобочную структуру :

Вот все правильные скобочные структуры с числом пар скобок 1, 2 и 3:

Определение 3.3.1. Числом Каталана cn называется число различных правильных скобочных структур из n пар скобок.

Удобно полагать c0 = 1. Тогда последовательность чисел Каталана начинается так:

Чтобы вывести производящую функцию для чисел Каталана, найдем сначала рекуррентное соотношение для этих чисел.

Всякая правильная скобочная структура удовлетворяет следующим двум условиям:

1. число левых и правых скобок в правильной скобочной структуре одинаково;

2. число левых скобок в любом начальном отрезке правильной скобочной структуры не меньше числа правых скобок.

Наоборот, всякая (конечная) последовательность левых и правых скобок, удовлетворяющая условиям 1 и 2, является правильной скобочной структурой.

В правильной скобочной структуре все скобки разбиваются на пары:

каждой левой скобке соответствует парная ей правая. Парная правая скобка выделяется следующим правилом: это первая правая скобка справа от данной левой скобки, такая, что между выбранными двумя скобками стоит правильная скобочная структура.

Рассмотрим в правильной скобочной структуре из n + 1 пар скобок пару скобок, в которую входит самая левая скобка структуры. Тогда последовательность скобок внутри этой пары образует правильную скобочную структуру и последовательность скобок вне этой пары образует правильную скобочную структуру: (. ). где каждое многоточие обозначает некоторую правильную скобочную структуру. Если число пар скобок во внутренней структуре равно k, то во внешней структуре n k пар скобок. Наоборот, по каждой паре скобочных структур из k и n k пар скобок можно восстановить структуру из n + 1 пар скобок, заключив первую структуру в скобки и приписав к результату справа вторую структуру.

Отсюда мы получаем рекуррентное соотношение для чисел Каталана.

На этот раз соотношение оказывается нелинейным (слагаемые в правой части являются произведениями элементов последовательности):

Например, при n = Рассмотрим производящую функцию для чисел Каталана Возведя ее в квадрат и умножив результат на s, получим что дает нам квадратное уравнение на производящую функцию (Второй корень квадратного уравнения отбрасывается, так как числитель 1 + 1 4s не делится на знаменатель 2s.) Вид производящей функции (3.3) позволяет найти явную формулу для чисел Каталана. Бином Ньютона в применении к выражению (1 4s)1/2 в числителе дает откуда, умножая числитель и знаменатель на n! и сокращая на 2n+1, получаем В частности, производящая функция для чисел Каталана не является рациональной формула для числа cn показывает, что это число не является квазимногочленом от n.

Последняя формула дает и более простое (хотя и с переменными коэффициентами) рекуррентное соотношение для чисел Каталана:

Числа Каталана перечисляют самые разнообразные комбинаторные объекты. Литература, им посвященная, необозрима. Известно несколько десятков их различных определений. Приведем лишь еще две часто встречающиеся их реализации.

Рассмотрим выпуклый (n + 2)-угольник, вершины которого занумерованы против часовой стрелки числами от 0 до n+1. Диагональной триангуляцией назовем разбиение многоугольника на треугольники непересекающимися диагоналями. Всякая такая триангуляция содержит n 1 диагоналей.

На рис. 3.6 приведены все различные диагональные триангуляции четырехугольника и пятиугольника.

число триангуляций (n + 2)-угольника при n 1; положим Пусть tn t0 = 1. Рассмотрим произвольную триангуляцию и выделим треугольник, примыкающий к стороне 01 (см. рис. 3.7 а)). Пусть k номер третьей Рис. 3.6: Диагональные триангуляции 4-х и 5-угольника Рис. 3.7: а) Треугольник, примыкающий к стороне 01, и б) перенумерация вершин многоугольников разбиения вершины этого треугольника. Выделенный треугольник разбивает (n + 2)угольник на k-угольник и (n k + 3)-угольник, каждый из которых триангулирован диагоналями. Перенумеруем вершины этих многоугольников против часовой стрелки так, чтобы нумерация вершин в каждом из них начиналась с 0 (см. рис. 3.7 б)). В результате получим пару триангуляций k-угольника и (n k + 3)-угольника.

Наоборот, каждая пара триангуляций k-угольника и (nk+3)-угольника определяет триангуляцию исходного многоугольника. Поэтому и, поскольку t0 = 1, последовательность чисел tn совпадает с последовательностью Каталана.

Описанная выше процедура сопоставления триангуляции (n+2)-угольника пары триангуляций k-угольника и (n k + 3)-угольника позволяет установить и взаимно-однозначное соответствие между триангуляциями (n+2)угольника и скобочными структурами из n пар скобок. Действительно, предположим, что для всех меньших значений n такое соответствие установлено. Каждой триангуляции (n+2)-угольника мы сопоставили пару триангуляций многоугольников с меньшим числом сторон. По предположению, этой паре триангуляций соответствует пара скобочных структур. Заключим первую из этих скобочных структур в скобки и припишем к ней вторую получим новую скобочную структуру, соответствующую исходной триангуляции всего (n + 2)-угольника.

Еще одна важная реализация чисел Каталана связана с путями Дика на те. Путем Дика1 называется непрерывная ломаная, составленная из векторов (1, 1) и (1, 1), начинающаяся в начале координат и заканчивающаяся на оси абсцисс (см. рис. 3.8).

Рис. 3.8: Путь Дика и соответствующая ему скобочная структура Совершенно ясно, как устанавливается соответствие между путями Дика и правильными скобочными структурами: нужно сопоставить вектору (1, 1) левую скобку, а вектору (1, 1) правую скобку (см. рис. 3.8). Тогда условие того, что путь лежит в верхней полуплоскости и заканчивается на оси абсцисс, и есть в точности условие правильности скобочной структуры.

Поэтому Число путей Дика из 2n звеньев равно n-му числу Каталана cn.

Тем самым, числа Каталана перечисляют пути из начальной вершины в вершины нижней строки в бесконечном графе, изображенном на рис. 3.9. В отличие от графов, пути в которых перечисляются коэффициентами рациональных производящих функций, этот граф содержит бесконечно много строк вершин.

Рис. 3.9: Граф, пути в котором перечисляются числами Каталана Пути Дика и их различные вариации имеют многочисленные интерпретации и не раз еще встретятся нам в этой книге.

1 Названы в честь немецкого математика Walther von Dyck (1856–1934). Произношение и русская транскрипция имени имеют варианты; возможны написания Дайк, Дейк, Дюк.

Задача 3.1. а) В графе на рис. 3.4 в вершину с номером 5 в нижнем ряду ведет 8 различных путей. Нарисуйте все эти пути. б) В графе на рис. 3.5 в вершину с номером 4 в нижнем ряду ведет 10 “различных” путей. Нарисуйте все эти пути.

Задача 3.2. Выпишите все 14 правильных скобочных структур из четырех пар скобок.

Задача 3.3. Пути Моцкина определяются так же, как и пути Дика, только они могут включать в себя горизонтальные векторы (1, 0) (см. рис. 3.10).

значается через mn. Вот начало последовательности Моцкина: m0 = 1, m1 = 1, m2 = 2, m3 = 4. Вычислите несколько следующих членов этой последовательности. Найдите для нее рекуррентное соотношение и производящую функцию.

Задача 3.4. Придумайте алгоритмы последовательного вывода а) правильных скобочных структур; б) путей Моцкина с данным количеством звеньев.

Задача 3.5. Рассмотрим множество путей на прямой, состоящих из шагов длины 1 вправо или влево. Найдите производящую функцию для числа таких путей из n шагов, начинающихся в 0 и а) оканчивающихся в 0; б) оканчивающихся в 0 и не заходящих в отрицательную полупрямую; в) оканчивающихся в фиксированной точке N 0; г) оканчивающихся в фиксированной точке N 0 и не заходящих в отрицательную полупрямую.

Задача 3.6. Рассмотрим множество путей на прямой, состоящих из шагов длины 2 вправо и шагов длины 1 влево. Найдите производящую функцию для числа таких путей из n шагов, начинающихся в 0 и а) оканчивающихся в 0; б) оканчивающихся в 0 и не заходящих в отрицательную полупрямую;

в) оканчивающихся в фиксированной точке N 0; г) оканчивающихся в фиксированной точке N 0 и не заходящих в отрицательную полупрямую.

Задача 3.7. В таблице из двух строк длины n расставлены числа от 1 до 2n, каждое по одному разу, так, что • в каждой строке числа возрастают;

• в каждом столбце числа возрастают (т.е. число, стоящее во второй строке, больше стоящего над ним).

Подсчитайте число таких расстановок.

Задача 3.8. Преобразованием Ганкеля последовательности , n = 0, 1, 2. называется последовательность hn = H(), состоящая из определителей Например, первые члены преобразования Ганкеля последовательности Каталана 1, 1, 2, 5. Catn. равны Докажите, что преобразование Ганкеля переводит а) последовательность Каталана в последовательность единиц 1, 1, 1. ; б) последовательность Каталана, начинающуюся с члена с номером 1, в последовательность единиц 1, 1, 1. ; в) последовательность Моцкина 1, 1, 2, 4. mn. (см. задачу 3.5) в последовательность единиц 1, 1, 1. г) Найдите преобразование Ганкеля последовательности Моцкина 1, 2, 4. mn+1. начинающейся с члена с номером 1.

Задача 3.9. Полимино (см. задачу 2.27) называется параллелограммным, если его граница представляет собой объединение двух ломаных, идущих вправо и вверх из общего левого нижнего конца в общий правый верхний конец, см. рис. 3.11. Докажите, что число параллелограммных полимино периметра 2n + 2 равно числу Каталана Catn.

Рис. 3.11: а) Параллелограммное полимино б) Пять параллелограммных полимино периметра Задача 3.10. Докажите, что производящая функция для чисел Каталана допускает следующее разложение:

Задача 3.11. Рассмотрим множество путей на плоскости, состоящих из векторов (1, 0), (1, 0), (0, 1). Найдите производящую функцию для числа таких путей длины n, начинающихся в 0 и несамопересекающихся (т.е. векторы (1, 0) и (1, 0) не могут идти непосредственно друг за другом).

Задача 3.12. Найдите произведение Адамара производящей функции для чисел Каталана и производящих функций а) 1s ; б) (1s)2 ; в) (1s)3.

Глава Производящие функции нескольких переменных Понятие производящей функции естественным образом распространяется на функции нескольких переменных. Производящие функции двух переменных отвечают двухиндексным последовательностям. Такие последовательности удобно записывать в виде треугольника (соответствующего положительному квадранту целочисленной решетки).

4.1 Треугольник Паскаля Треугольник Паскаля изображен на рис. 4.1. Элементы этого треугольника перечисляют пути, идущие из его вершины в соответствующую клетку. Пути имеют вид ломаных, составленных из векторов единичной длины двух видов: идущих вправо-вниз и идущих влево-вниз.

Числа, стоящие в треугольнике Паскаля, это уже хорошо знакомые нам биномиальные коэффициенты Это несложно доказать индукцией по n. Предположим, что числа в n-й строчке треугольника совпадают с коэффициентами разложения многочлена (1+s)n. Число различных путей, ведущих в точку (n+1, k), равно сумме числа путей, ведущих в точку (n, k 1), и числа путей, ведущих в точку (n, k), cn+1,k = cn,k1 + cn,k. Поэтому число cn+1,k совпадает с коэффициентом при sk в многочлене (1 + s) · (1 + s)n = (1 + s)n+1.

Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую Рис. 4.1: Треугольник Паскаля а), пути, которые он перечисляет б) и возможные нумерации его элементов в), г) функцию Второй способ соответствует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис. 4.1 г)). Для этой нумерации и производящая функция имеет вид На этот раз она оказалась симметричной по переменным x и y.

И, наконец, имеется еще один способ: сопоставить треугольнику Паскаля экспоненциальную производящую функцию. Экспоненциальная произЭкспоненциальные производящие функции водящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности an, а числа an /n!. Экспоненциальные производящие функции заслуживают отдельного обсуждения, к которому мы сейчас и переходим.

4.2 Экспоненциальные производящие функции Зафиксируем произвольную последовательность . Каждой последовательности мы можем сопоставить производящую функцию определяемую последовательностью . Если в последовательности отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались только обычными производящими функциями отвечающими последовательности n 1. В зависимости от преследуемых целей пользу могут принести и другие последовательности. Чаще всего используется последовательность n = n!. Соответствующие ей производящие функции называются экспоненциальными.

Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операций над ними. Сумма ведет себя обычным образом:

а вот произведение иначе:

Коэффициенты произведения вычисляются по формуле Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных (и интегрировании).

Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их величины:

Обычная производящая функция A(s) = a0 +a1 s+a2 s2 +. выражается через экспоненциальную A(t) = a0 + a1 t + a2 t2 +. по формуле Действительно, Теперь мы можем выписать экспоненциальную производящую функцию для треугольника Паскаля:

Треугольник Дика перечисляет пути в положительном квадранте плоскости, выходящие из начала координат и составленные из векторов (1, 1) и (1, 1) (см. рис. 4.2). Пути, оканчивающиеся на оси абсцисс, это пути Дика из раздела 3.3.

Рис. 4.2: Треугольник Дика и пути, которые он перечисляет Нетрудно видеть, что элементы dij треугольника Дика отличны от нуля в том и только в том случае, если i j и i + j четно. Обозначим через D(x, y) производящую функцию Дика двух переменных Правило построения треугольника Дика подсказывает нам уравнение на эту производящую функцию Действительно, коэффициент при любом мономе xi y j, отличном от единичного, представляет собой сумму коэффициентов при мономах xi1 y j Мы знаем, что коэффициенты разложения правой части по степеням переменной x являются многочленами от y, хотя из формулы это совершенно не очевидно.

4.4 Треугольник Бернулли–Эйлера и перечисление up-down перестановок Треугольник Бернулли–Эйлера (рис. 4.3), как и треугольник Паскаля, обладает многими замечательными свойствами. Левая сторона этого треугольника называется стороной Бернулли, правая стороной Эйлера1.

Рис. 4.3: Треугольник Бернулли–Эйлера и пути, которые он перечисляет Элементы треугольника Бернулли–Эйлера тоже числа путей из вершины треугольника в данную клетку. Но при этом рассматриваются только пути, идущие зигзагом: нечетные шаги влево, четные вправо. Поэтому каждое число в треугольнике Бернулли–Эйлера равно сумме чисел предыдущей строки, стоящих слева или справа от него, в зависимости от четности строки.

Можно дать и более простое индуктивное правило определения чисел в треугольнике Бернулли–Эйлера, если чередовать знаки через каждые две строчки (см. рис. 4.4). В таком альтернированном треугольнике каждый 1 Отметим, что есть еще две последовательности чисел, которые также носят имена Бернулли и Эйлера.

элемент равен сумме двух ближайших элементов, стоящих справа и справа сверху от него. Для того чтобы однозначно задать треугольник, необходимо доопределить сторону Эйлера, чем мы сейчас и займемся.

Рис. 4.4: Альтернированный треугольник Бернулли–Эйлера Нам понадобится еще одна интерпретации треугольника Бернулли–Эйлера в терминах up-down перестановок.

Определение 4.4.1. Перестановка на множестве называется пилообразной, или up-down перестановкой, если каждый элемент в ней либо больше, либо меньше обоих своих соседей.

Например, перестановка (3, 2, 7, 1, 6, 4, 5) пилообразная. Вот все пилообразные перестановки для n = 2, 3, 4, 5, в которых последний элемент меньше своего левого соседа (а значит, первый элемент больше своего правого соседа, если n четно, и меньше его, если n нечетно):

(1, 3, 2, 5, 4) (1, 4, 2, 5, 3) (1, 4, 3, 5, 2) (1, 5, 2, 4, 3) (1, 5, 3, 2, 4) (2, 3, 1, 5, 4) (2, 4, 1, 5, 3) (2, 4, 3, 5, 1) (2, 5, 1, 4, 3) (2, 5, 3, 4, 1) (3, 4, 1, 5, 2) (3, 4, 2, 5, 1) (3, 5, 1, 4, 2) (3, 5, 2, 4, 1) (4, 5, 1, 3, 2) (4, 5, 2, 3, 1) Тем самым, последовательность, перечисляющая пилообразные перестановки, последний элемент в которых меньше своего левого соседа, начинается так: 1, 1, 2, 5, 16. Это в точности те числа, которые стоят по сторонам треугольника Бернулли–Эйлера: числа с четными номерами ненулевые элементы стороны Бернулли, а числа с нечетными номерами ненулевые элементы стороны Эйлера. В дальнейшем мы будем рассматривать только такие пилообразные перестановки, в которых последний элемент меньше своего левого соседа, и не будем это специально оговаривать, называя их просто пилообразными перестановками.

Чтобы понять, откуда берется связь с треугольником Бернулли–Эйлера, рассмотрим пилообразные перестановки, первый элемент в которых равен k.

Лемма 4.4.2. Пусть cn,k число up-down перестановок на множестве , начинающихся с n + 1 k. Тогда cn,k есть k-е число в n-й строке треугольника Бернулли–Эйлера.

Например, как видно из предыдущего списка, среди пилообразных перестановок пяти элементов 5 начинаются с 1, еще 5 с двойки, 4 с тройки, 2 с четверки и ни одна не начинается с пятерки. Строка 0, 2, 4, 5, 5 совпадает с четвертой строкой треугольника Бернулли–Эйлера.

Доказательство. Для первых двух строк треугольника утверждение проверяется непосредственно. Докажем, что если оно верно для n-й строки, то оно верно и для строки с номером n+1. Пусть, для определенности, n+ четно. Тогда n и n+2 нечетны; мы изучаем перестановки из n+1 элементов.

Первый элемент в такой перестановке является локальным максимумом, второй минимумом, поэтому второй элемент меньше первого.

Отбрасывание первого элемента в перестановке после перенумерации остальных элементов с сохранением их относительного порядка дает однозначно определенную up-down перестановку на множестве из n элементов.

Наоборот, по каждой пилообразной перестановке множества , первый элемент в которой равен l k, можно построить пилообразную перестановку множества , первый элемент в которой равен k:

допишем k слева и увеличим на 1 все элементы k, k + 1. n.

Таким образом, Для строки с нечетным номером справедливо аналогичное рассуждение.

Тем самым, числа cn,k удовлетворяют тем же соотношениям, что и элeменты треугольника Бернулли–Эйлера, а значит, именно они и стоят в этом треугольнике.

Выведем теперь производящие функции для сторон треугольника Бернулли–Эйлера. Рассмотрим по отдельности два случая:

• n нечетно; соответствующее число up-down перестановок обозначим через bn и введем экспоненциальную производящую функцию • n четно; соответствующее число up-down перестановок обозначим через en и введем экспоненциальную производящую функцию Выведем рекуррентную формулу для числа up-down перестановок. Максимальный элемент в пилообразной перестановке разделяет ее на две перестановки, каждая из которых является пилообразной нужно лишь перенумеровать элементы в левой и правой части перестановки, сохраняя их относительный порядок. Например, (2, 7, 3, 9, 1, 6, 5, 8, 4) ((2, 7, 3), (1, 6, 5, 8, 4)) ((1, 3, 2), (1, 4, 3, 5, 2)).

В результате мы сопоставили каждой пилообразной перестановке на множестве из n + 1 элементов две пилообразные перестановки на множестве из k и из n k элементов, n k нечетно.

При нечетном n получаем рекуррентное соотношение на числа bn :

Биномиальный коэффициент возникает из-за того, что при склеивании двух up-down перестановок мы должны всеми возможными способами распределить номера по левой и правой частям перестановки, т.е. выбрать из n номеров те, которые соответствуют левой перестановке.

Вспоминая, что для экспоненциальных производящих функций правая часть соответствует квадрату производящей функции B(x), а левая ее же производной, перепишем уравнение (4.1) в виде Нетрудно проверить, что у этого уравнения есть единственное решение, разложение которого начинается с B(x) = x +. Такое решение мы знаем это тангенс, поскольку (tg x) = tg2 x + 1.

Таким образом, сторона Бернулли определяет разложение в ряд тангенса:

Коэффициенты bn в разложении тангенса называются тангенциальными числами. Обратите внимание на то, что единица в вершине треугольника не включается в сторону Бернулли.

Замечание 4.4.3. Уравнение (4.2) несложно и решить непосредственно. Вспомнив, что B (x) = dB/dx, имеем Если же n четно, то рекуррентное соотношение принимает вид и ему соответствует уравнение на производящие функции. Решая последнее уравнение, получаем и сторона Эйлера определяет разложение в ряд секанса. Коэффициенты en этого разложения называются числами Эйлера 2.

Воспользовавшись подстановкой мы можем переписать производящие функции сторон для альтернированного треугольника в виде Теперь у нас есть все необходимое для вычисления экспоненциальной производящей функции альтернированного треугольника Бернулли–Эйлера. Обозначим через bek,l элемент треугольника, имеющий координату k вдоль стороны Бернулли и координату l вдоль стороны Эйлера.

«ЧТО КНИГА ГОВОРИТ О СПОРТЕ СТЮАРТ ВИЕР 1 Эту книгу я посвящаю моим детям, Кристин и Джонатану, чьи занятия спортом были для меня огромным источником радости. 2 ЧТО КНИГА ГОВОРИТ О СПОРТЕ СТЮАРТ ВИЕР 3 БЛАГОДАРНОСТЬ Я признателен всем людям, благодаря которым стало возможным создание этой книги. Я благодарен Наоми Старки из издательства Байбл ридинг феллоушип (BRF) за предложение написать подобную книгу и за е ободрение во время процесса работы над ней. В течение 10 лет я был сотрудником. »

«tv-программа совет чудесная сюрпризы стр. 7-8, 17-18 дает ответ механотерапия осени афиша стр. 3 стр. 22 стр. 12 стр. 16 ОЛГИЕ Издается с августа 2000 года РУДЫ № 38 (127) пятница, 25 сентября 2009 года Еженедельная городская газета http://ia-dolpr.mosoblonline.ru Картинки с выставки С 23 по 26 сентября в Международном выставочном центре Крокус Экспо проходит шестая межотраслевая Международная выставкапрезентация Московской области ПодмосковьеНынешний год для Московской области особенный –. »

«Энциклопедия намаза Издание 2-е Библиотека Рисалат Москва 2011 Редакционный совет: сотрудники канонического отдела ДУМД Курамухаммад-хаджи Рамазанов Мангуев Магомед-хаджи Мутаилов Магди-хаджи Ахмедов Камалудин-хаджи Исаев Ахмед-хаджи Мирзоев Магомед-Шамиль-хаджи Магомедов Мухаммад-Ханапи-хаджи Саадуев Мухаммадрасул-хаджи Давудов Мухаммад-хаджи Гамзатов Зайнулла-хаджи Магомедов Мухаммад-хаджи Канонический редактор: Магомедов Абдуламагомед Магомедович Составитель: Омаров Магомедрасул Магомедович. »

«РОССИЙСКИЙ МОРСКОЙ РЕГИСТР СУДОХОДСТВА УТВЕРЖДАЮ Генеральный директор М.Г. Айвазов 19.07.2013 Условия, принципы и цели сертификации систем менеджмента Организаций НД № 2-070101-008 32B Дата введения в действие: 01.09.2013 Номер документа в СЭД Тезис – 115624 Разработчик: 327 Санкт — Петербург 2013 РОССИЙСКИЙ МОРСКОЙ РЕГИСТР СУДОХОДСТВА Условия, принципы и цели сертификации систем менеджмента Организаций Издание: Оглавление 1 Область распространения 2 Нормативные ссылки 3 Термины. Определения. »

«-1Глория Поло Свидетельство От иллюзии к истине Я стояла перед вратами рая и ада Перевод с немецкого: Dr. Gloria Polo Von der Illusion zur Wahrheit Ich stand an der Pforte des Himmels und der Holle Испанский оригинал: Testimonio de Gloria Polo Интернет: www.gloriapolo.net или Apostolat ANE, Postfach 102 AT-1011 Wien, Austria Перевел с немецкого: Д-р Йосип Марцелич -2СВИДЕТЕЛЬСТВО ГОСПОЖИ ДР. ГЛОРИИ ПОЛ Несчастье, случившееся во время грозы Доброе утро, Слава Богу, дорогие братья и сестры! Я. »

«RU 2 457 002 C1 (19) (11) (13) РОССИЙСКАЯ ФЕДЕРАЦИЯ (51) МПК A61M 16/01 (2006.01) A61B 5/0488 (2006.01) A61K 31/4468 (2006.01) A61B 5/0476 (2006.01) A61K 31/5517 (2006.01) A61K 31/135 (2006.01) A61K 31/05 (2006.01) A61K 31/47 (2006.01) A61K 31/4168 (2006.01) ФЕДЕРАЛЬНАЯ СЛУЖБА ПО ИНТЕЛЛЕКТУАЛЬНОЙ СОБСТВЕННОСТИ A61K 31/13 (2006.01) A61K 31/02 (2006.01) A61P 23/00 (2006.01) (12) ОПИСАНИЕ ИЗОБРЕТЕНИЯ К ПАТЕНТУ (21)(22) Заявка: 2011103585/14, 01.02.2011 (72) Автор(ы): Лебедева Майя Николаевна (RU). »

«КАНОНИЧЕСКИЕ ТЕКСТЫ ПУШКИНА В ЛИРИКЕ И РОМАНЕ БОРИСА ПАСТЕРНАКА КОНСТАНТИН ПОЛИВАНОВ 1. Тема с вариациями У Пастернака пушкинские аллюзии и реминисценции встречаются, как у любого поэта ХХ в., на протяжении всего его литературного пути: и в одном из первых опубликованных стихотворных текстов Февраль. Достать чернил и плакать. и в стихотворениях первой книги стихов Венеция и Близнецы (см. [Баевский: 171–188; Гаспаров, Поливанов: 79, 90]), и во многих позднейших текстах. Во второй книге. »

«Эллисон Пирсон И как ей это удается? OCR Альдебаран http://www.litres.ru/pages/biblio_book/?art=121062 И как ей это удается?: Фантом Пресс; Москва; 2004 ISBN 5-86471-345-7 Оригинал: AllisonPearson, “I dont know how she does it” Перевод: Елена Е. Ивашина Аннотация Знакомьтесь: Кейт Редди, фондовый менеджер и мать двоих детей. Она может делать десять дел одновременно: продавать и покупать акции, менять пеленки, выяснять отношения с мужем, отбиваться от тупого босса, стряпать пироги, следить за. »

«R CDIP/13/10 ОРИГИНАЛ: АНГЛИЙСКИЙ ДАТА: 27 МАРТА 2014 Г. Комитет по развитию и интеллектуальной собственности Тринадцатая сессия Женева, 19-23 мая 2014 г. ГИБКИЕ ВОЗМОЖНОСТИ В ПАТЕНТНОЙ СФЕРЕ, ПРЕДУСМОТРЕННЫЕ В МНОГОСТОРОННЕЙ НОРМАТИВНОЙ БАЗЕ, И ИХ РЕАЛИЗАЦИЯ В ЗАКОНОДАТЕЛЬСТВЕ НА НАЦИОНАЛЬНОМ И РЕГИОНАЛЬНОМ УРОВНЕ ЧАСТЬ III подготовлено Секретариатом В контексте обсуждения Рекомендации 14 Повестки дня в области развития на 1. одиннадцатой сессии Комитета по развитию и интеллектуальной. »

«Выпуск № 21, 2013 МЕЖДУНАРОДНЫЙ ЛИТЕРАТУРНЫЙ АЛЬМАНАХ ИЗДАЁТСЯ ПРИ УЧАСТИИ БЕЛОРУССКОГО ФОНДА МИРА ББК 84 Ч82 Коллектив авторов: В. Акатов, О. Биченкова, А. Бондаревский, И. Борисова, И. Брагин, Л. Браташ, Л. Варакина, В. Григоров, А. Гущин, А. Долинов, Г. Ежова, Л. Жеглова, А. Зайнутдинова, С. Земцов, О. Иванова-Захарова, Ю. Ишков, Е. Казмировский, Т. Квитко, И. Киреев, О. Кириллов, Е. Кондратьева, З. Коровин, А. Кудинова, Т. Лагутёнок, К. Ландышева, Д. Либерман, А. Лосева, Т. Лукьянчук, Н. »

«165 Рита Осиповна Мазель учитель русского языка и литературы, исследователь творчества Ф. М. Достоевского (Москва, Российская Федерация) levinanadya@mail.ru. СЦЕНЫ СЧАСТЬЯ В РОМАНАХ ДОСТОЕВСКОГО Аннотация: В предлагаемой статье Достоевский предстает перед чи­ тателем как поэт счастья. Пережив уникальный опыт страданий, он по­ стиг иное измерение жизни. Со страстью первооткрывателя он утвержда­ ет благодать живой жизни. Жизнь — дар, жизнь — счастье, каждая минута может быть веком счастья, — вот. »

«016446 B1 Евразийское (19) (11) (13) патентное ведомство ОПИСАНИЕ ИЗОБРЕТЕНИЯ К ЕВРАЗИЙСКОМУ ПАТЕНТУ (12) (51) Int. Cl. C07D 401/12 (2006.01) (45) Дата публикации и выдачи патента A61K 31/4545 (2006.01) 2012.05.30 A61P 9/12 (2006.01) (21) Номер заявки 2010000 (22) Дата подачи заявки 2008.06. ПРОИЗВОДНЫЕ N5-(2-ЭТОКСИЭТИЛ)-N3-(2-ПИРИДИНИЛ)-3,5ПИПЕРИДИНДИКАРБОКСАМИДА, ПРЕДНАЗНАЧЕННЫЕ ДЛЯ ПРИМЕНЕНИЯ В КАЧЕСТВЕ ИНГИБИТОРОВ РЕНИНА (56) WO-A-2007/ (31) 07012412.8; 07111290. WO-A-2007/ (32) 2007.06.25;. »

«У Н И В Е Р С И Т Е Т С К А Я Б И Б Л И О Т Е К А А Л Е К С А Н Д Р А П О Г О Р Е Л Ь С К О Г О С Е Р И Я Ф И Л О С О Ф И Я ЭРНСТ МА Х А Н А Л ИЗ О Щ У ЩЕНИЙ И ОТ Н ОШ ЕН ИЕ Ф И З И Ч Е СК О ГО К П С ИХ ИЧЕС К О МУ МОСКВА Т Е Р Р И Т О Р И Я Б УД У Щ Е Г О УДК ББК 87. М СОСТАВИТЕЛИ СЕРИИ: В. В. Анашвили, Н. С. Плотников, А. Л. Погорельский НАУЧНЫЙ СОВЕТ: А. Л. Глазычев, А. И. Уткин, А. Ф. Филиппов, Р. З. Хестанов М 36 Эрнст Мах. Анализ ощущений. »

«Аналитический отчёт LiveInternet для сайта buhgalter.kz за март 2013 г. Базовые месячные показатели посещаемости сайта: Просмотров страниц 192,652 (-24% мес/мес) Посетителей 52,085 (-13% мес/мес) Доля женщин 71.4 % Доля мужчин 28.6 % Посетители младше 18 лет 3.3 % Посетители от 18 до 24 лет 23.5 % Посетители от 25 до 34 лет 31.6 % Посетители от 35 до 44 лет 22.2 % Посетители старше 44 лет 19.3 % Преобладающая страна — Казахстан 79.8 % Структура переходов на страницы сайта: Внутренние 51.1 %. »

«ОРГАНИЗАЦИЯ A ОБЪЕДИНЕННЫХ НАЦИЙ ГЕНЕРАЛЬНАЯ АССАМБЛЕЯ Distr. GENERAL A/HRC/8/41 28 May 2008 RUSSIAN Original: ENGLISH СОВЕТ ПО ПРАВАМ ЧЕЛОВЕКА Восьмая сессия Пункт 6 повестки дня УНИВЕРСАЛЬНЫЙ ПЕРИОДИЧЕСКИЙ ОБЗОР Доклад Рабочей группы по универсальному периодическому обзору Швейцария* * Ранее издан под условным обозначением A/HRC/WG.6/2/L.7; незначительные исправления были внесены по поручению секретариата Совета по правам человека на основе редакционных изменений, сделанных государствами по. »

«ФОНД РУССКИЙ МИР РУССКАЯ ШКОЛЬНАЯ БИБЛИОТЕЧНАЯ АССОЦИАЦИЯ (РШБА) ЧТО ЧИТАТЬ ДОШКОЛЬНИКАМ И МЛАДШИМ ШКОЛЬНИКАМ КРУГ ЧТЕНИЯ * ЧТО ЧИТАТЬ ДОШКОЛЬНИКАМ И МЛАДШИМ ШКОЛЬНИКАМ Рекомендательный указатель детской литературы МОСКВА РШБА * Затраты на реализацию проекта покрыты за счет Гранта, предоставленного фондом Русский мир. СОДЕРЖАНИЕ Об указателе детской литературы ЧТО ЧИТАТЬ ДОШКОЛЬНИКАМ И МЛАДШИМ ШКОЛЬНИКАМ Тихомирова И.И. Обращение к читателям ЧТО ЧИТАТЬ ДОШКОЛЬНИКАМ И МЛАДШИМ ШКОЛЬНИКАМ 1. »

«XIV Всероссийский научный форум 24–27 сентября Мать и Дитя 2013 Москва, МВЦ Крокус Экспо V cъезд акушеров-гинекологов России Научная программа q ОРГАНИЗАТОРЫ: Министерство здравоохранения Российской Федерации ФГБУ Научный центр акушерства, гинекологии и перинатологии имени академика В.И. Кулакова Министерства здравоохранения Российской Федерации Российское общество акушеров-гинекологов Конгресс-оператор ООО МЕДИ Экспо 24–27 сентября, 2013 XIV Всероссийский научный форум V cъезд. »

«RU 2 445 135 C1 (19) (11) (13) РОССИЙСКАЯ ФЕДЕРАЦИЯ (51) МПК A61N 5/00 (2006.01) A61N 2/04 (2006.01) A61K 35/02 (2006.01) A61P 15/02 (2006.01) ФЕДЕРАЛЬНАЯ СЛУЖБА ПО ИНТЕЛЛЕКТУАЛЬНОЙ СОБСТВЕННОСТИ (12) ОПИСАНИЕ ИЗОБРЕТЕНИЯ К ПАТЕНТУ (21)(22) Заявка: 2010131765/14, 28.07.2010 (72) Автор(ы): Юрьев Сергей Юрьевич (RU), (24) Дата начала отсчета срока действия патента: Валькевич Ольга Михайловна (RU), 28.07.2010 Рузаева Юлия Федоровна (RU), Большанова Оксана Витальевна (RU), Приоритет(ы): Мустафина. »

«УДК 316.774:39(497.11)2001/2007 32.019.5:39(497.11)2001/2007 Срђан Радовић Етнографски институт САНУ Етнологија у медијима транзиционе Србије Струјање знања и порука спроводи се у многољудним друштвеним заједницама преко читавог низа институционализованих канала комуникације и друштвене социјализације, који – макар одавали утисак демократичности и доступности због своје опште присутности – и у 21. веку већином функционишу захваљујући, пре свега, ограниченом броју креатора и медијатора знања и. »

«Постановление Правительства Республики Казахстан от 16 января 2012 года № 72 Об утверждении Правил предоставления услуг почтовой связи и Правил применения почтового штемпеля на почтовых отправлениях В соответствии с подпунктами 5) и 7) пункта 1 статьи 8 Закона Республики Казахстан от 8 февраля 2003 года О почте Правительство Республики Казахстан ПОСТАНОВЛЯЕТ: 1. Утвердить прилагаемые: 1) Правила предоставления услуг почтовой связи; 2) Правила применения почтового штемпеля на почтовых. »

© 2014 www.kniga.seluk.ru — «Бесплатная электронная библиотека — Книги, пособия, учебники, издания, публикации»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

🎥 Видео

Задача, которую исключили из экзамена в АмерикеСкачать

11 класс, 49 урок, Задача ЭйлераСкачать

#225. КВАТЕРНИОНЫ и углы ЭйлераСкачать

Теория вероятностей | Математика TutorOnlineСкачать

Закон БернуллиСкачать

Формула БернуллиСкачать

Этой задачей русские дети 10 лет мучили американцев. Американцы не понимали, что делают не такСкачать

Прямая ЭйлераСкачать

Гипотеза Римана - Numberphile на русском.Скачать

Функция ЭйлераСкачать

Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Малая теорема Ферма и теорема Эйлера | Ботай со мной #037 | Борис Трушин !Скачать

Окружность Эйлера (окружность 9 точек) и прямая ЭйлераСкачать

Схема испытаний Бернулли | Теория вероятностейСкачать

ФОРМУЛА БЕРНУЛЛИ. ТЕОРИЯ ВЕРОЯТНОСТЕЙСкачать

Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать