Треугольник abc является изображением

Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.

Просмотр содержимого документа
«Контрольная работа № 2 по теме «Параллельность в пространстве» (10 класс, Мерзляк А.Г. и др.)»

Контрольная работа № 2 по теме «Параллельность в пространстве»

1 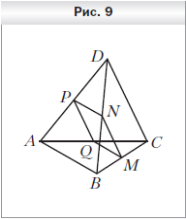. Точки M, N, P и Q — середины отрезков BC, BD, AD и AC соответственно, AB = 14 см, CD = 18 см (рис. 9). Определите вид четырёхугольника MNPQ и вычислите его периметр.

2. Плоскость α пересекает стороны AB и BC треугольника ABC в точках M и K соответственно и параллельна стороне AC, MK = 4 см, MB : MA = 2 : 3. Найдите сторону AC треугольника.

3 . Треугольник ABC является изображением правильного треугольника A₁B₁C₁ (рис. 10). Постройте изображение высоты треугольника, опущенной на сторону A₁C₁.

4. Плоскости α и β параллельны. Из точки M, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости α и β в точках A₁ и B₁, а другой — в точках A₂ и B₂ соответственно. Найдите отрезок B₁B₂ , если он на 2 см больше отрезка A₁A₂ , MB₁ = 7 см, A₁B₁ = 4 см.

5. Точки A, B, C, не лежащие на одной прямой, являются параллельными проекциями трёх последовательных вершин правильного шестиугольника. Постройте изображение этого шестиугольника.

1 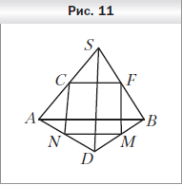. Точки F, M, N и C — середины отрезков BS, DB, AD и AS соответственно, SD = 30 см, AB = 36 см (рис. 11). Определите вид четырёхугольника FMNC и вычислите его периметр.

2. Плоскость β пересекает стороны AB и AC треугольника ABC в точках N и D соответственно и параллельна стороне BC, AD = 6 см, DN : CB = 3 : 4. Найдите сторону AC треугольника.

3 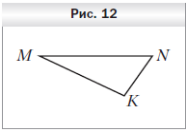. Треугольник MNK является изображением правильного треугольника M₁N₁K₁ (рис. 12). Постройте изображение биссектрисы треугольника, проведённой из вершины M₁.

4. Плоскости α и β параллельны. Через точку M, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках A₁ и B₁, а другая — в точках A₂ и B₂ соответственно. Найдите отрезок A₁A₂ , если он на 1 см меньше отрезка B₁B₂ , MA₂ = 4 см, A₂B₂ = 10 см.

5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин квадрата и его центра. Постройте изображение квадрата.

1 . Точки N, M, C и K — середины отрезков BD, DF, FA и AB соответственно, BF = 24 см, AD = 18 см (рис. 13). Определите вид четырёхугольника NMCK и вычислите его периметр.

2. Плоскость α пересекает стороны MF и MK треугольника MFK в точках A и B соответственно и параллельна стороне FK,
AB = 12 см, AM : AF = 3 : 5. Найдите сторону FK треугольника.

3 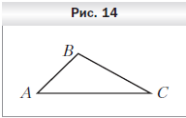. Треугольник ABC является изображением правильного треугольника A₁B₁C₁ (рис. 14). Постройте изображение центра вписанной окружности треугольника A₁B₁C₁.

4. Плоскости α и β параллельны. Из точки O, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости α и β в точках C₁ и D₁, а другой — в точках C₂ и D₂ соответственно. Найдите отрезок C₁C₂, если он на 5 см меньше отрезка D₁D₂, OC₁ = 4 см,
C₁D₁ = 10 см.

5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин правильного треугольника и его центра. Постройте изображение этого треугольника.

В 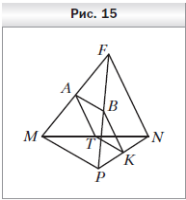ариант 4

1. Точки A, B, K и T — середины отрезков MF, PF, PN и MN соответственно, MP = 10 см, FN = 16 см (рис. 9). Определите вид четырёхугольника ABKT и вычислите его периметр.

2 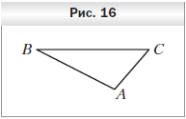. Плоскость β пересекает стороны CF и CD треугольника CDF в точках M и N соответственно и параллельна стороне FD, MN = 6 см, FD = 21 см, MC = 10 см. Найдите сторону FC треугольника.

3. Треугольник ABC является изображением правильного треугольника A₁B₁C₁ (рис. 16). Постройте изображение центра описанной окружности треугольника A₁B₁C₁.

4. Плоскости α и β параллельны. Через точку D, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках M₁ и N₁, а другая — в точках M₂ и N₂ соответственно. Найдите отрезок M₁M₂ , если он на 8 см больше отрезка N₁N₂ , N₁M₁= 30 см, DN₁ = 5 см.

5. Точки A, B и M, не лежащие на одной прямой, являются соответственно параллельными проекциями двух соседних вершин параллелограмма и середины его противолежащей стороны. Постройте изображение этого параллелограмма.

Видео:№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

Интегрированный урок (геометрия + черчение) по теме «Изображение пространственных фигур на плоскости». 10-й класс

Класс: 10

План урока

Цели урока

1. Образовательные цели: изучение понятия «параллельное проецирование» и его свойств, формирование навыков построения изображений плоских и пространственных фигур на плоскости с помощью аксонометрической проекции, развитие умений сравнивать явления
2. Развивающие цели:развитие абстрактного мышления, пространственного воображения и интуиции, развитие познавательного интереса и интереса к поисково-исследовательской деятельности.
3. Воспитательные цели:развитие навыков коллективной работы, создание атмосферы доброжелательности на уроке.

Оборудование: компьютер, учебный диск, интерактивная доска, проектор, модели плоских геометрических фигур.

Ход урока

1. Организационный момент.

Учитель математики: Сегодня у нас с Вами необычный урок. Сегодня на нашем уроке встретятся геометрия и черчение. Тема нашего урока «Изображение пространственных фигур на плоскости».

2. Актуализация знаний учащихся с помощью дидактической игры «Верно – неверно». Этап сопровождается показом слайдовой презентации (приложение 1).

Учитель математики: Чтобы работа на уроке была плодотворной, давайте вспомним некоторые факты, характеризующие свойства параллельных прямых и плоскостей. Ваша задача определить верность следующих высказываний. Итак, начинаем.

1. Верно ли, что через любую точку пространства можно провести множество прямых параллельных данной прямой?

По теореме о существовании прямой, параллельной данной прямой через точку пространства можно провести единственную прямую.

2. Верно ли, что если одна из двух параллельных прямых пересекает плоскость, то и другая тоже пересекает эту плоскость?

По лемме о пересечении плоскости двумя параллельными прямыми, если одна из параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

3. Верно ли, что две непересекающиеся прямые в пространстве параллельны?

В пространстве не имеют общих точек параллельные и скрещивающиеся прямые.

4. Верно ли, что если две прямые параллельны некоторой плоскости, то они параллельны друг другу?

Эти прямые могут быть не только параллельными, но и пересекаться, а также они
могут быть скрещивающимися.

3. Определение целей урока с помощью учащихся проводит учитель черчения.

Вы заметили, что дать точный ответ нам помогли чертежи. Надеюсь, что никто из Вас не станет отрицать того, что «хороший» чертёж всегда поможет нам в решении геометрических задач, но в то же время все построения на уроках черчения Вы выполняете на основе математических законов. Главной задачей нашего сегодняшнего урока будет понять, что требуется знать, чтобы наши чертежи всегда были правильными и «хорошими».

4. Историческая справка о проективной геометрии, параллельном проецировании.

Учитель черчения: Параллельная проекция всем хорошо знакома. Солнце находится от нас так далеко, что его лучи в любой момент времени можно считать практически параллельными. Поэтому тень от любого предмета на дороге или стене дома представляет собой проекцию этого предмета на плоскость дороги или стены параллельно лучам солнца (рис.1).

Учитель черчения: с помощью презентации рассказывает о параллельной проекции (косоугольной и прямоугольной), о создателе начертательной геометрии Гаспаре Монже (1746-1818) (рис.2) и Ж.Дезарге (1593-1662).

5. Поисково-исследовательская деятельность учащихся.

На этом этапе необходимо выяснить свойства параллельной проекции.

Учителя предлагают поиграть в театр теней.

— Как во всяком театре у нас должны быть актёры. Сегодня все роли Ваши.

(Распределяются роли, раздаются эскизы фигур – «героев» действия: точка, прямая, отрезок, треугольник, параллелограмм, круг, и.т.д.)

Жили-были на свете геометрические фигуры: точки, прямые, отрезки, углы, треугольники, параллелограммы, трапеции и окружности. Они были очень дружными фигурами и всегда помогали друг другу. Однаждыв город привезли новое развлечение – ЗЕРКАЛО ПАРАЛЛЕЛЬНЫХ ПРОЕКЦИЙ. И все жители городка отправились в него посмотреться. Первой пришла Точка.

— Что Вы, уважаемая Точка, увидели в зеркало?

(Ученица рассказывает, что получается при проекции точки на плоскость).

Следом за ней прибежала красавица Прямая.

— А что Вы увидели, дорогая Прямая?

(Ученица рассказывает, что получается при проекции прямой на плоскость).

Очень заинтересовался зеркалом весёлый Отрезок.

— Что же интересного мог увидеть наш приятель?

Он увидел отрезок, но совсем другой длины, которая менялась в зависимости от того как он поворачивался. (Желательно, чтобы ученик самостоятельно сделал этот вывод).

А уж когда к нему присоединился его братишка — второй Отрезок, так веселью не было конца. Повертелись они в своё удовольствие. И пересекались, и становились параллельными. И всё это изобразилось в проекционном зеркале.

— Что интересного Вы увидели?

(Учитель выясняет различные случаи изображения двух отрезков).

Но тут пришёл Знайка, которому тоже было очень интересно посмотреть на это зеркало. Он тут же попросил братьев Отрезков помочь ему провести маленький эксперимент. Знайка разделил отрезок в отношении 2:1 и проверил, изменится ли это соотношение в зеркале.

— Уважаемый, Знайка, что же Вы увидели?

(Делается вывод о сохранении отношений длин отрезков).

Слава о зеркале быстро разнеслась по всему городку. Неспеша, подошел к этому чуду дядюшка Угол. И очень обиделся.

— Что Вас так обидело, уважаемый дядюшка Угол?

(Делается вывод о несохранении градусных мер углов).

Следом за ним прибежали Треугольник, Параллелограмм, Прямоугольник, Окружность и Трапеция.

— Что же Вы все увидели в этом чудо – зеркале?

(С каждой геометрическ5ой фигурой выясняется, что представляют их проекции).

Долго не смолкало веселье в маленьком городке геометрических фигур, а мы с Вами давайте подведём итоги.

Так какие же свойства фигур сохраняются при параллельном проецировании?

А какие не сохраняются? (Итоги подводятся с помощью презентации).

При параллельном проецировании сохраняются следующие свойства фигур

1. Свойство фигуры быть точкой, прямой и плоскостью.
2. Свойство фигур иметь пересечение.
3. Деление отрезка в данном отношении.
4. Параллельность прямых и плоскостей.
5. Свойство фигуры быть треугольником, параллелограммом, трапецией.
6. Отношение длин параллельных отрезков.
7. Отношение площадей двух фигур.

При параллельном проецировании не сохраняются следующие свойства фигур:

1. Свойство прямых и плоскостей образовывать между собой углы определенной градусной меры (в частности быть взаимно перпендикулярными).
2. Отношение длин не параллельных отрезков.
3. Отношение величин углов между прямыми (в частности, свойство луча быть биссектрисой угла).

Текст свойств высвечивается на интерактивной доске по мере их выявления. У учащихся на столах лежат памятки с перечислением этих свойств.

1. Проекция точки есть точка.
2. Проекция прямой есть прямая (рис.3).
3. Проекция отрезка есть отрезок (рис.4).
4. Проекции параллельных отрезков – параллельные отрезки или отрезки, принадлежащие одной прямой (рис.5).
5. Проекции параллельных отрезков, а также проекции отрезков, лежащих на одной прямой, пропорциональны самим отрезкам (рис.6).

Учитель математики: Теперь выясним как изображаются фигуры в аксонометрической проекции. По рисунку 7 попробуйте сформулировать алгоритм построения произвольной плоской фигуры с помощью параллельного проектирования.

А теперь поговорим об изображении определённых плоских фигур.

Произвольный отрезок на чертеже можно считать изображением данного отрезка.

В качестве изображения данного треугольника на чертеже можно брать произвольный треугольник (рис.8).

Изображением равнобедренного и прямоугольного треугольников может служить разносторонний треугольник (рис.9).

Изображением данного параллелограмма можно считать произвольный параллелограмм (рис.10).

В частности изображением прямоугольника, ромба и квадрата будет параллелограмм.

Изображение трапеции
Изображением трапеции является трапеция, у которой основания пропорциональны основаниям самой трапеции (рис. 11).

Изображением равнобедренной трапеции может быть и неравнобедренная трапеция.

Параллельной проекцией окружности является эллипс (рис.12).

Эллипс используют при изображении на плоскости цилиндров, конусов, усечённых конусов и сфер.

6. Практическое применение теоретических знаний. Решение задач

Учитель математики: Следующим шагом в нашей работе будет этап решения задач, лежащих в основе правильного изображения пространственных фигур в параллельной проекции. (Для решения задач используются возможности интерактивной доски. Текст всех задач лежит на столах учащихся).

Задача 1. Треугольник ABC является параллельной проекцией треугольника A₁B₁C₁. В треугольнике A₁B₁C₁ проведены из вершины A₁ биссектриса, медиана и высота. Будут ли проекции этих отрезков соответственно биссектрисой, медианой и высотой?

Задача 2. Построить изображение правильного треугольника и изображение высоты и биссектрисы угла А (решение на рис.13 и рис.14).

Задача 3. Треугольник ABC – параллельная проекция правильного треугольника. Построить проекцию серединного перпендикуляра к стороне АС. Построить проекцию перпендикуляра, проведенного из вершины С к стороне АС.

Задача 4. Трапеция ABCD – параллельная проекция равнобедренной трапеции. Построить ось симметрии и высоту данной трапеции (решение на рис.15 и рис.16).

Задача 5. Дана параллельная проекция ромба. Построить параллельную проекцию прямых, проведённых через середину стороны перпендикулярно диагоналям (решение на рис.17 и рис.18).

Задача 6. Начертите параллельную проекцию ромба, имеющего угол в 60°. Постройте изображение высоты этого ромба, проведенной: а) из вершины острого угла; б) из вершины тупого угла.

7. Заключительный этап урока. Выводы. Подведение итогов

Фронтальная беседа с учащимися.

1. Что называется параллельной проекцией точки, отрезка, треугольника, окружности?
2. Какие величины не изменяются при параллельном проецировании? (длина отрезка, градусная мера углов, отношения длин отрезков).
3. Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?

8. Задание на дом

1. Построить с помощью параллельной проекции: а) изображение правильного шестиугольника; б) изображение правильного восьмиугольника.
2. Дан произвольный треугольник. Считая его изображением прямоугольного треугольника, начертить изображение квадратов, построенных на катетах и гипотенузе.

Видео:Задача 6 №27350 ЕГЭ по математике. Урок 42Скачать

Дано изображение некоторого треугольника и центра его описанной окружности, расположенного внутри треугольника. Постройте изображение

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Ваш ответ

Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

решение вопроса

Видео:🔴 В треугольнике ABC проведена биссектриса ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,029
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

📽️ Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Задание 6 ЕГЭ по математике. Урок 17Скачать

Решение задачи №1 из ЕГЭ математикаСкачать

№103. Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой.Скачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

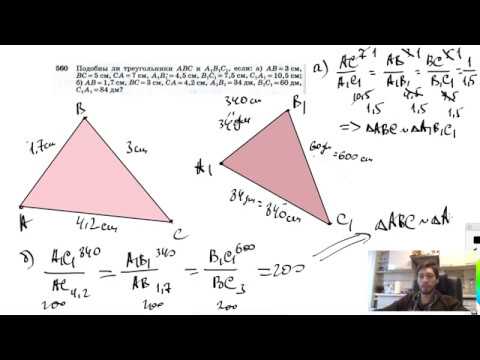
№560. Подобны ли треугольники ABC и A1B1C1, если: а) АВ = 3 см, ВС=5 см, СА=7 см, А1В1=4,5см,Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Задание 6 ЕГЭ по математике. Урок 13Скачать

8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать