Треугольник 30 градусов вписан в окружность

Задание 6. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30°. Найдите сторону AB этого треугольника.

Расширенная теорема синусов гласит, что

,

где a, b, c – соответствующие стороны треугольника; R – радиус описанной вокруг него окружности. Отсюда следует, что сторона AB, равна:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Треугольник вписанный в окружность

Видео:Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Равнобедренный треугольник АВС с углом А, равным 30 градусов, вписан в окружность?

Геометрия | 10 — 11 классы

Равнобедренный треугольник АВС с углом А, равным 30 градусов, вписан в окружность.

Найти градусную меру меньшей из дуг АС?

Так как угол А равен тридцать градусов, то угол С также равен 30 град (свойство равнобедренного треугольника).

Следовательно угол В равен 180 — 30 — 30 = 120 градусов.

Дуга, на котрую опирается угол, также равна 240 градусов (120 / 2).

Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Треугольник АВС вписан в окружность с центром в точке О?

Треугольник АВС вписан в окружность с центром в точке О.

Найти градусную меру угла С треугольника АВС, если угол АОВ равен 115 градусов.

Видео:ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Вписанный угол на 45 градусов меньше центрального угла, опирающегося на ту же дугу окружности?

Вписанный угол на 45 градусов меньше центрального угла, опирающегося на ту же дугу окружности.

Найдите градусную меру вписанного угла.

Видео:Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Найдите градусную меру вписанного в окружность угла АВС, если градусная мера дуги АС равна : а)72 градус ; б)56градус ; в)126градус ; г)200градус?

Найдите градусную меру вписанного в окружность угла АВС, если градусная мера дуги АС равна : а)72 градус ; б)56градус ; в)126градус ; г)200градус.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

СРОЧНО Помогите пожалуйста)Градусная мера угла ABC вписанного в окружность равна 65 градусов, а дуга равна AB равна 112 градусов?

СРОЧНО Помогите пожалуйста)

Градусная мера угла ABC вписанного в окружность равна 65 градусов, а дуга равна AB равна 112 градусов.

Найдите градусную меру дуги BC.

Видео:Треугольник, вписанный в окружность геометрия 7 классСкачать

Вписанный угол на 25 градусов меньше центрального угла, опирающегося на ту же дугу окружности?

Вписанный угол на 25 градусов меньше центрального угла, опирающегося на ту же дугу окружности.

Найдите градусную мер вписанного угла.

Видео:Окружность || Часть 4 || Треугольник, вписанный в окружностьСкачать

Треугольник ABC вписан в окружность так, что градусные меры дуг AB и AC равны соответственно 120 и 150 градусам?

Треугольник ABC вписан в окружность так, что градусные меры дуг AB и AC равны соответственно 120 и 150 градусам.

Найдите углы треугольника.

Видео:Треугольник ABC вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Вписанный угол на 25 градусов меньше центрального угла, опирающегося на ту же дугу окружности?

Вписанный угол на 25 градусов меньше центрального угла, опирающегося на ту же дугу окружности.

Найдите градусную мер вписанного угла.

Видео:Вписанный в окружность прямоугольный треугольник.Скачать

Равнобедренный треугольник АВС с углом В равным 76 градусов вписан в окружность?

Равнобедренный треугольник АВС с углом В равным 76 градусов вписан в окружность.

Найдите градусную меру меньшей из дуг ВС.

Видео:В окружности проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.Скачать

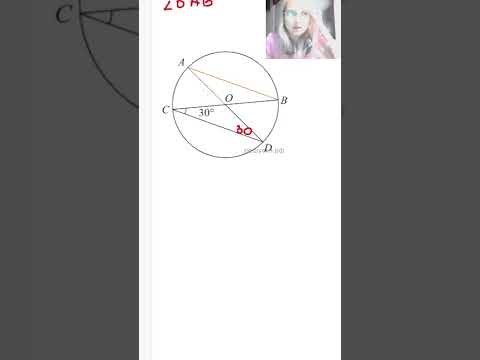
Треагольник АВС вписан в окружность так, что градусные меры дуг АВ и АС равны соответственно 100 и 140 градусам?

Треагольник АВС вписан в окружность так, что градусные меры дуг АВ и АС равны соответственно 100 и 140 градусам.

Найдите углы треугольника.

Видео:Треугольник и окружность #shortsСкачать

Как найти углы равнобедренного треугольника вписанного в окружность , боковая сторона которого стягивает дугу, градусная мера которой 38?

Как найти углы равнобедренного треугольника вписанного в окружность , боковая сторона которого стягивает дугу, градусная мера которой 38.

Вопрос Равнобедренный треугольник АВС с углом А, равным 30 градусов, вписан в окружность?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

1) ∠OAB = ∠ABO = 45°⇒AO = BO = a 2)∠CAO = ∠ACO = 45°⇒CO = AO = a 3)BC² = a² + a² — 2a * a * cos120° cos120° = — 1 / 2⇒ BC² = 2a² + a² = 3a²⇒ BC = a√3.

📹 Видео

найти угол треугольника вписанного в окружность с центром на сторонеСкачать

2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать

Угол 30 градусов в прямоугольном треугольникеСкачать

Треугольник вписанный в окружностьСкачать