Тренажер окружность 8 класс (3 видео) | Курс школьной геометрии

Тренажер по геометрии для учеников 8 класса по разделу «Окружность».

Содержание

«Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Дистанционное обучение как современный формат преподавания
Математика: теория и методика преподавания в образовательной организации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Оставьте свой комментарий
Подарочные сертификаты
Подборка задач по теме «Окружность. Касательная. Вписанные и центральные углы» тренажёр по геометрии (8 класс) на тему
Скачать:
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
Тренажер по теме «Окружности»
Просмотр содержимого документа «Тренажер по теме «Окружности»»
📺 Видео

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тренажер по теме «Окружность» 8 класс Инструкция Вам предложены 30 заданий. 12 из них с выбором ответа. К каждому заданию есть подсказки, которые напомнят теоремы, определения или свойства. Прежде чем воспользоваться подсказкой или посмотреть в ответ, попытайся справиться с заданием сам. Желаю успеха при подготовке!

А Подсказка Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Б В Г

Подсказка А Б В Г Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).

Подсказка А Б В Г Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника. В этом случае треугольник называют треугольником, описанным около окружности.

Подсказка А Б В Г Окружностью, описанной около четырехугольника, называют окружность, проходящую через все вершины четырёхугольника. В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.

Подсказка А Б В Г Окружность называется описанной около треугольника, если она проходит через все его вершины.

Подсказка А Б В Г Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех его сторон.

Подсказка А Б В Г Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.

Подсказка А Б В Г

Подсказка В любом вписанном четырехугольнике суммы противоположных углов равны 180°. А Б В Г

В любом вписанном четырехугольнике суммы противоположных углов равны 180°. Подсказка А Б В Г

Подсказка Четыре замечательные точки в треугольнике: 1) три медианы пересекаются в одной точке, являющейся центром тяжести треугольника; 2) три биссектрисы пересекаются в одной точке (центре вписанной окружности); 3) три высоты (или их продолжения) пересекаются в одной точке («ортоцентре»); 4) три серединных перпендикуляра пересекаются в одной точке (центре описанной окружности). А Б В Г

Расстояние d=7(см), r = 16 : 2 = 8(см) d 15 слайд

Если расстояние от центра окружности до прямой меньше радиуса окружности (d 16 слайд r1 + r2 о. » title=»Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 о. «> r1 + r2 о» title=»Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 о»>

Расстояние между центрами окружностей больше суммы их радиусов d > r1 + r2 общих точек нет Подсказка 2 общие точки Нет общих точек Ответ

2 общие точки Нет общих точек Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 18 слайд

Определение 1. Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами. Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами. Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу. Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. ∟АСВ- вписанный, значит равен половине дуги АВ, следовательно АВ= 120° Подсказка Ответ

Определение 1. Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами. Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами. Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу. Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. ∟АВС- вписанный, значит равен половине дуги АС, то есть АС= 140°. Следовательно центральный ∟АОС= 140°. Подсказка Ответ

Определение. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Теорема. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Обратная(признак). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является касательной. Свойство. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. 3 4 4 4 Р∆АВС =22(см) Подсказка Ответ

Теорема. Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Подсказка Ответ 8

В любом описанном четырехугольнике суммы противоположных сторон равны. Подсказка АВ + DC = AD + BC Ответ

Определение 1. Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами. Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами. Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Следствие1. Вписанные углы, опирающиеся на одну и ту же дугу равны. Следствие 2. Вписанный угол, опирающийся на полуокружность — прямой. ∟DBC = 90° Подсказка Ответ

Вписанный угол, опирающийся на полуокружность — прямой. 8 8 r r Подсказка Ответ

Теорема. Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Подсказка Ответ 4 2 * 6 = 3 * 4 АС = 7(см)

Подсказка Ответ Вписанный угол, опирающийся на полуокружность — прямой. 3 r 3 а

Теорема. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Подсказка Ответ 4 4

Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами. Подсказка Ответ

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр Середина гипотенузы прямоугольного треугольника является центром описанной около этого треугольника окружности. АВ2 = 82 + 62 = 100 АВ = 10(cм) r=5(см) Подсказка Ответ

Если что- то не получилось сразу, то не отчаивайся. Можно потренироваться еще раз. У тебя все получится.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 931 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 702 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 333 человека из 72 регионов

Ищем педагогов в команду «Инфоурок»

Тренажер по геометрии для учеников 8 класса по разделу «Окружность». Презентация содержит 30 заданий и вопросов. 12 из них с выбором ответа, только один из четырех ответов верный, под ним скрывается веселый смайл, под остальными- грустный. Каждый вопрос снабжен подсказкой. Может быть использован при любом УМК по геометрии как в 8-х классах, так и в выпускных при подготовке к экзамену. Цель: повторить и обобщить пройденный материал, повысить познавательный интерес у обучающихся.

Перед началом тестирования нужно ознакомиться с инструкцией, расположенной на первом слайде презентации. Ссылки «инструкция», «подсказка» и «ответ» первым нажатием по кнопке открываются, а вторым- скрываются. Переход к следующему слайду осуществляется щелчком по свободному полю.

Носкова Светлана АльбертовнаНаписать 4511 24.01.2015

Номер материала: 334087

24.01.2015 656

24.01.2015 706

24.01.2015 434

24.01.2015 2828

24.01.2015 1064

24.01.2015 748

24.01.2015 1741

Не нашли то, что искали?

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме обсудят введение обязательных тестов на наркотики в школах

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России ежегодно будут обучать плаванию не менее 500 тыс. детей

Время чтения: 2 минуты

Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет

Время чтения: 3 минуты

Детский омбудсмен предложила ужесточить наказание за преступления против детей

Время чтения: 1 минута

Более половины россиян сталкиваются с конфликтами в родительских чатах

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Подборка задач по теме «Окружность. Касательная. Вписанные и центральные углы»
тренажёр по геометрии (8 класс) на тему

16 опорных задач по теме «Окружность. Касательная. Вписанные и центральные углы» взяты на учебной платформе Дмитрия Гущина «Решу ОГЭ» и для удобства применения на уроке оформлены в виде таблицы. Ниже — таблица ответов.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Скачать:

Вложение	Размер
okruzhnost._zadachi.docx	191.47 КБ

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Предварительный просмотр:

Окружность. Касательная к окружности. Вписанные и центральные углы.

Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC , если BD = 1 см, а радиус окружности равен 5 см.

Найдите величину (в градусах) вписанного угла α , опирающегося на хорду AB , равную радиусу окружности.

В треугольнике ABC угол C равен 90°, AC = 30 , BC = 5 Найдите радиус окружности, описанной около этого треугольника.

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD , если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.

Рисунок выполнить самостоятельно

На окружности с центром O отмечены точки A и B так, что ∠ AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.

Рисунок выполнить самостоятельно

Прямая касается окружности в точке K . Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK . Ответ дайте в градусах.

Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO . Ответ дайте в градусах.

Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠ C , если ∠ A = 44°. Ответ дайте в градусах.

Из точки А проведены две касательные к окружности с центром в точке О . Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.

В окружности с центром в точке О проведены диаметры AD и BC , угол OCD равен 30°. Найдите величину угла OAB .

В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B . На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB .

На окружности по разные стороны от диаметра AB взяты точки M и N . Известно, что ∠ NBA = 38°. Найдите угол NMB . Ответ дайте в градусах.

Найдите площадь квадрата, описанного вокруг окружности радиуса 7.

Окружность с центром в точке O описана около равнобедренного треугольника ABC , в котором AB = BC и ∠ ABC = 66°. Найдите величину угла BOC . Ответ дайте в градусах.

В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD . Ответ дайте в градусах.

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

По теме: методические разработки, презентации и конспекты

Вписанные и центральные углы

Активизация самостоятельности познавательной деятельности учащихся. Формирование навыков коллективной работы, развитие чувства ответственности за свои знания.

Разработка урока «Вписанные и центральные углы» 8 класс

Данная разработка включает в себя конспект урока, презентацию к уроку, самостоятельную работу, тест.

Вписанные и центральные углы

«Вписанные и центральные углыУрок изучения нового материала с применением мультимедийной презентации.

Тест по геометрии «Вписанные и центральные углы»

Тест по геометрии для учащихся 8 класса состоит из 12 заданий: выбор одного из предложенных ответов, краткая запись ответа, соответствие. На последний слайд выводится результат о решённых заданиях и в.

«Окружность. Вписанные и центральные углы.»

Презентация к уроку геометрии 8 -го класса. Материал может быть использован как в 8 классе, так и в 9 классе при подготовке к ОГЭ.

Урок по геометрии «Вписанные и центральные углы» 8 класс

Урок подготовки учащихся к успешной сдачи ОГЭ.

Тест по теме «Вписанные и центральные углы».

Тест по теме «Вписанные и центральные углы». Предназначен для повторения темы «Вписанные и центральные углы» при подготовке к ОГЭ. Состоит из 7 заданий для 2 вариантов.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Тренажер по теме «Окружности»

Тренажер состоит из 2х видов заданий. В первой части необхъодимо соронесмти определение и понятие. Важно! Тут используются макросы. Вторая часть — это задачи в виде теста

Просмотр содержимого документа
«Тренажер по теме «Окружности»»

группы МИБ-51 Мартынова А. В.

— множество всех точек плоскости, удаленных на заданное расстояние (равное радиусу) от заданной точки этой же плоскости.

— отрезок, соединяющий точки окружности с центром.

— отрезок, соединяющий любые две точки окружности.

— хорда, проходящая через центр окружности.

— часть плоскости, ограниченная окружностью.

— это часть окружности ограниченная двумя точками.

Макрос создан программистом Хансом Хофманом (Германия)

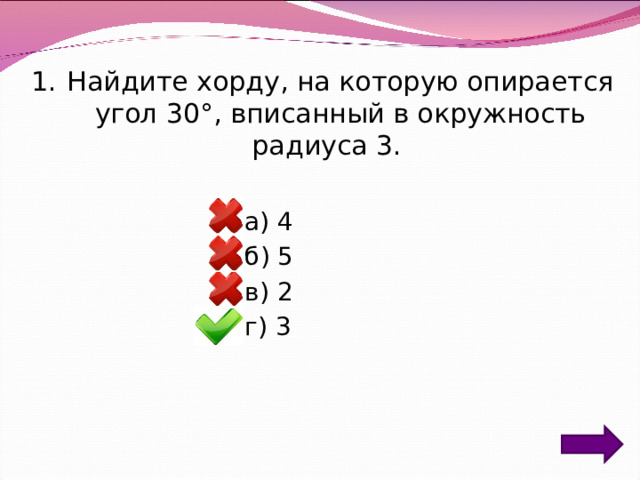
Найдите хорду, на которую опирается угол 30°, вписанный в окружность

2. Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

3. В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 110°. Найдите вписанный угол ACB. Ответ дайте в градусах.

4. Найдите вписанный угол, опирающийся на дугу, которая составляет 1/5 окружности. Ответ дайте в градусах.

5. Найдите угол , если вписанные углы и опираются на дуги окружности, градусные величины которых равны соответственно 118˚ и 38˚. Ответ дайте в градусах.

6. Дуга окружности AC, не содержащая точки B, составляет 200°. А дуга окружности BC, не содержащая точки A, составляет 80°. Найдите вписанный угол ACB. Ответ дайте в градусах.

7. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

8. Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

9. Найдите угол ACO, если его сторона CA касается окружности, дуга АВ — равна 64°. Ответ дайте в градусах.

10. Угол ACO равен 24°. Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.