Траектория движения протона в однородном магнитном поле представляет собой окружность

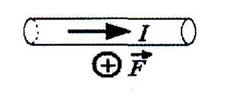
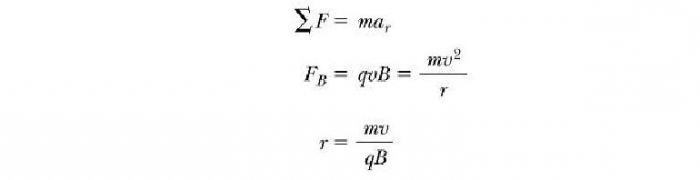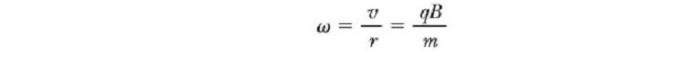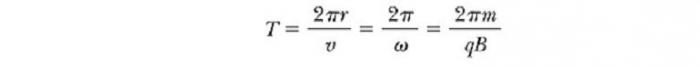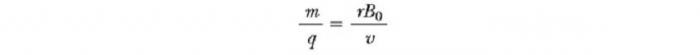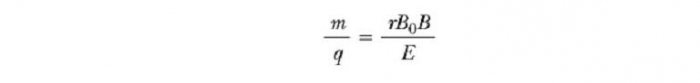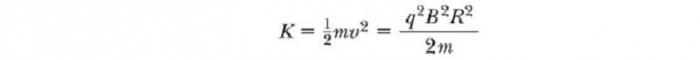27.1. В однородном магнитном поле на горизонтальный проводник с током, направленным вправо, действует сила Ампера, направленная перпендикулярно плоскости рисунка от наблюдателя. При этом линии магнитной индукции поля направлены …

ВАРИАНТЫ ОТВЕТОВ:

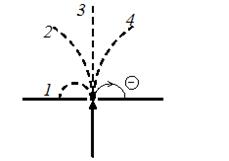
27.2. Вблизи длинного прямолинейного проводника с током I (на рисунке ток направлен от нас) пролетает электрон. Указать направление силы Лоренца, действующей на электрон в точке С.

ВАРИАНТЫ ОТВЕТОВ:

1) сила равна нулю;

27.3. Траектория движения протона в однородном магнитном поле представляет собой окружность, расположенную в плоскости рисунка. Если протон вращается по часовой стрелке, то линии магнитной индукции поля направлены …

ВАРИАНТЫ ОТВЕТОВ:

1) ;

2) ;

3) ;

4) .

27.4. В магнитное поле влетает электрон и движется по дуге окружности. Протон, влетевший в это поле с такой же скоростью, будет двигаться по траектории …

ВАРИАНТЫ ОТВЕТОВ:

1) 2 ; 2) 1 ; 3) 3 ; 4) 4 .

27.5. В однородном магнитном поле на горизонтальный проводник с током, направленным вправо, действует сила Ампера, расположенная в плоскости чертежа и направленная вверх. При этом линии магнитной индукции поля направлены …

ВАРИАНТЫ ОТВЕТОВ:

27.6. Три прямых па­рал­лель­ных бесконечно длинных про­вод­ни­ка с равными по силе токами I лежат в одной плос­ко­сти на рас­сто­я­нии а друг от друга. Cила Ампе­ра, дей­ству­ю­щая на про­вод­ник 1 со стороны двух других проводников, направлена .

ВАРИАНТЫ ОТВЕТОВ:

27.7. Три прямых па­рал­лель­ных бесконечно длинных про­вод­ни­ка с равными по силе токами I лежат в одной плос­ко­сти на рас­сто­я­нии а друг от друга. Cила Ампе­ра, дей­ству­ю­щая на про­вод­ник 1 со стороны двух других проводников, направлена .

ВАРИАНТЫ ОТВЕТОВ:

27.8. Прямоугольная рамка расположена в плоскости чертежа и способна вращаться вокруг вертикальной оси , лежащей в её плоскости, как показано на рисунке. По рамке течёт постоянный электрический ток I. Если рамку внести в постоянное однородное магнитное поле , то действующие на рамку силы Ампера стремятся .

ВАРИАНТЫ ОТВЕТОВ:

2) рас­тя­нуть рамку;

3) по­вер­нуть рамку во­круг оси по часовой стрелке;

4) по­вер­нуть рамку во­круг оси против часовой стрелки;

5) од­но­вре­мен­но сжать рамку и по­вер­нуть её во­круг оси по часовой стрелке;

6) од­но­вре­мен­но растянуть рамку и по­вер­нуть её во­круг оси против часовой стрелки.

27.9. Прямоугольная рамка расположена в плоскости чертежа и способна вращаться вокруг вертикальной оси , лежащей в её плоскости, как показано на рисунке. По рамке течёт постоянный электрический ток I. Если рамку внести в постоянное однородное магнитное поле , то действующие на рамку силы Ампера стремятся.

ВАРИАНТЫ ОТВЕТОВ:

1) по­вер­нуть рамку во­круг оси против часовой стрелки;

2) рас­тя­нуть рамку;

4) по­вер­нуть рамку во­круг оси по часовой стрелке;

5) од­но­вре­мен­но сжать рамку и по­вер­нуть её во­круг оси по часовой стрелке;

6) од­но­вре­мен­но растянуть рамку и по­вер­нуть её во­круг оси против часовой стрелки.

27.10. Поле создано двумя параллельными бесконечно длинными проводниками с токами I₁=I₂=I. Через точку А пролетает протон, как показано на рисунке. Сила, действующая на протон, направлена .

ВАРИАНТЫ ОТВЕТОВ:

27.11. Траектория движения протона в однородном магнитном поле представляет собой окружность, расположенную в плоскости рисунка. Если протон вращается по часовой стрелке, то линии магнитной индукции поля направлены …

ВАРИАНТЫ ОТВЕТОВ:

27.12. В однородное поле влетают перпендикулярно линиям магнитной индукции протон, электрон и нейтрон. На приведенном рисунке показаны траектории их движения. Установить соответствие между приведённой траекторией движения и соответствующей частицей.

ВАРИАНТЫ ОТВЕТОВ:

1) 1 – нейтрону, 2 – протону, 3 – электрону;

2) 1 – протону, 2 – электрону, 3 – нейтрону;

3) 1 – электрону, 2 – нейтрону, 3 – протону;

4) 1 – протону, 2 – нейтрону, 3 – электрону;

5) 1 – нейтрону, 2 – электрону, 3 – протону;

6) 1 – электрону, 2 – протону, 3 – нейтрону.

27.13. Две частицы q₁ и q₂ с одинаковыми скоростями влетают в однородное магнитное поле под углами α₁= 30° и α₂ = 60° соответственно к линиям магнитной индукции. Если q₂ =3q₁ , то сила Лоренца, действующая на первую частицу . , чем сила, действующей на вторую частицу.

ВАРИАНТЫ ОТВЕТОВ:

1) в раз меньше; 2) в раз больше;

3) в раз меньше; 4) в раза больше;

5) в раз меньше ; 6) в раз больше.

Видео:Физика - Магнитное полеСкачать

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Видео:Движение электронов в магнитном поле - Сила ЛоренцаСкачать

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Видео:Рамка с током в магнитном поле. 8 класс.Скачать

Движение заряженных частиц в однородном магнитном поле

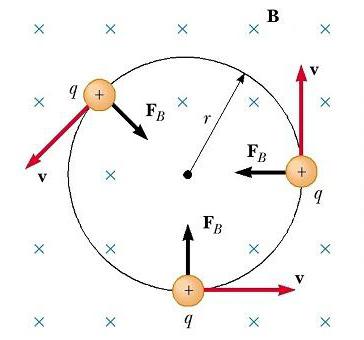
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Видео:МАГНИТНОЕ ПОЛЕ за 24 минуты. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

Движение частицы под углом к вектору магнитного поля

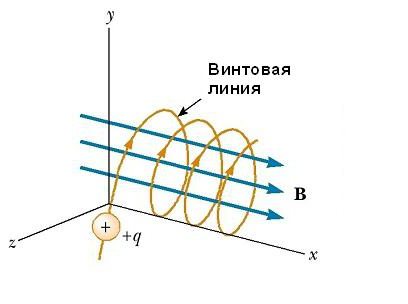
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Неоднородное магнитное поле: как в нем движутся частицы

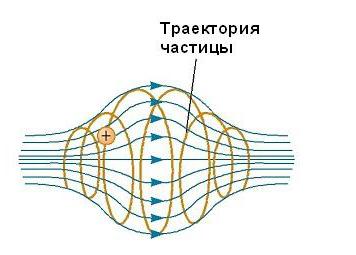
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Видео:урок магнитное поле и силы 01Скачать

Как Земля влияет на движение космических частиц

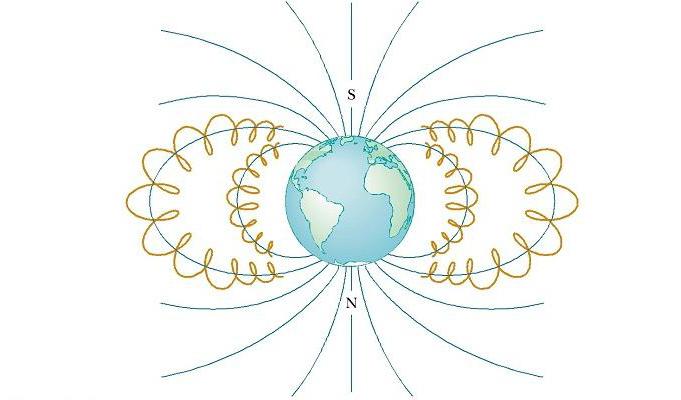
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Видео:Действие магнитного поля на движущийся заряд. Сила Лоренца | Физика 11 класс #3 | ИнфоурокСкачать

Селектор скоростей

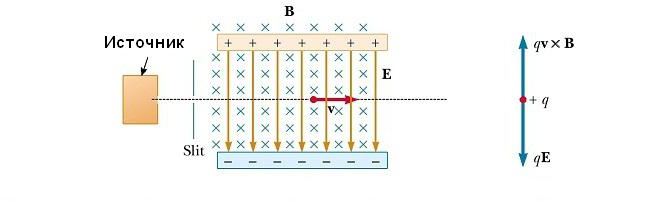
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Видео:Движение заряженных частиц Лекция 9-2Скачать

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Видео:Сила ЛоренцаСкачать

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

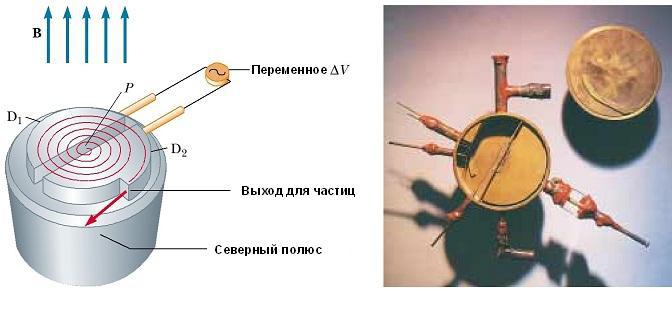
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Видео:Теория движения заряженных частиц в электрическом поле .Часть 1Скачать

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Видео:ЕГЭ. Физика. #Урок11. Магнитное поле. Сила Ампера. Сила ЛоренцаСкачать

Что такое циклотрон, его принцип работы, устройство и применение

Знаете ли вы, что самый большой в мире ускоритель частиц, БАК (Большой адронный коллайдер), находится в ЦЕРНе недалеко от Женевы, точнее, на границе Франции и Швейцарии? На рисунке 1 показана аэрофотосъемка с окружностью туннеля, находящегося на глубине 100 м под землей, длиной около 27 км, в котором протоны разгоняются до скорости — 0,999999991 от скорости света.

Рис. 1. Пунктирная линия показывает границу между Францией и Швейцарией. На более близком плане мы видим аэропорт Женевы.
[ Источник: Максимильен Брис (ЦЕРН) / CC BY-SA ].

ЦЕРН (Европейская организация ядерных исследований) была создана в 1953 году и объединяет 20 государств-членов.

Ученые со всего мира приезжают в ЦЕРН, проводят эксперименты по столкновениям частиц на БАК, на основе которых они хотят ответить на главный вопрос: «Какова природа нашей Вселенной, из чего она состоит?».

На рисунке 2 показаны снимки из туннеля БАК. Именно вдоль проложенной «трубы», в ее центральной части, параллельно друг другу проходят встречные вращающиеся пучки протонов. В определенных точках этого пути, где расположены детекторы, протоны пересекаются и происходят их столкновения.

На рисунке 3 показан «открытый» (фото относится к периоду сборки этой мощной конструкции) детектор CMS. Кроме него, есть еще три: ATLAS, ALICE и LHCb.

Рис. 3. Источник фото: [ Tighef / CC BY-SA ]

Очень интересно, но как это связано с названием этой статьи… Ну, циклотрон — это, можно сказать, прототип ускорителя в ЦЕРНе. Циклотрон, о котором мы будем говорить здесь, является простейшим циклическим ускорителем.

Циклотрон — это резонансный циклический ускоритель нерелятивистских тяжёлых заряженных частиц (протонов, ионов), в котором частицы движутся в постоянном и однородном магнитном поле, а для их ускорения используется высокочастотное электрическое поле неизменной частоты.

Циклотрон не подходит для получения энергий, значительно превышающих энергию покоя частиц. Поэтому он не используется для ускорения электронов.

Циклотрон используется в физике для запуска ядерных реакций. Но его также используют в медицине. Здесь он используется для получения радионуклидов в диагностических целях. В Германии, например, имеется около 25 циклотронных установок для производства этих радионуклидов.

Видео:23.10.2020. Физика (угл.). 11 класс. Скачкова Т. В.Скачать

Принцип работы циклотрона

В наиболее часто используемых ускорителях заряженных частиц — циклических ускорителях — для ускорения частиц мы используем как электрические, так и магнитные поля. Сначала это может показаться странным, ведь магнитное поле не способно ускорить частицу.

Магнитная сила, часто называемая силой Лоренца, действующая на частицу, движущуюся в магнитном поле, перпендикулярна вектору скорости υ и, следовательно, перпендикулярно вектору перемещения Δr . Если мы напишем определение работы силы F в виде A_F = F * Δr * cos∡( F , Δr ), то мы видим, что работа силы, действующей под углом 90° к перемещению тела, равна нулю. Поэтому и работа магнитной силы (всегда!) равна нулю. Эта сила не может изменить кинетическую энергию заряженной частицы — она не может ускорить ее. Вместо этого она меняет направление своего движения! И именно этот факт используется в циклических ускорителях — циклотронах.

Идея ускорения заряженной частицы в электрическом поле показана на рисунке 4.

Рис. 4. Ускорение частицы в электрическом поле

Положительно заряженная частица попадает в электрическое поле. На нее действует электрическая сила, направленная в виде линий поля (вектор напряженности электрического поля E ) в соответствии со скоростью частицы — частица ускоряется.

Давайте воспользуемся энергетическим подходом. Электрическая сила совершает положительную работу над частицей. Эта работа, как работа результирующей силы, действующей на частицу, равна увеличению кинетической энергии частицы. Мы можем записать: A_el = ΔE_k .

Мы можем выразить работу электрического поля через разность потенциалов между точками поля, пересекаемыми частицей: A_el = q * ( V + — V — ) где V + — потенциал положительного электрода, а V — — потенциал отрицательного электрода. Разность этих потенциалов равна U.

Наибольшее генерируемое напряжение, полученное с помощью генераторов Ван де Граафа, примененных к модулю ускорения частиц, составляет около 10 МВ. Поэтому протон, выходящий из такого модуля, будет иметь кинетическую энергию 10 МэВ. Если мы хотим придать ему больше энергии, мы должны много раз «пропустить» его через модуль ускорения. Это происходит, например, в линейном ускорителе, в котором модули расположены последовательно.

Вы можете использовать магнитное поле, чтобы развернуть частицу и заставить ее пройти через тот же ускоряющий модуль. Конечно, вы можете делать это многократно, вызывая многократное увеличение кинетической энергии частицы. В конце концов, частица приобретет кинетическую энергию E_k = n * e * U, где n — число эпизодов прохождения частицы через электрическое поле. Этой блестящей идеей мы обязаны создателю циклотрона Эрнесту Лоуренсу (см. рисунок 5), который в 1939 году получил за свое изобретение Нобелевскую премию.

Рис. 5. Первый циклотрон, построенный Лоуренсом около 1930 года. Его диаметр составлял 4 дюйма. Он передал энергию в 80 кэВ ионизированным молекулам водорода

Видео:Урок 277. Масс-спектрограф. Циклотрон. Магнитный щит ЗемлиСкачать

Устройство циклотрона

Циклотрон, по сути, состоит из пары дуантов. Это металлические, полые электроды D-образной формы каждый. Их лучше всего представить себе как части плоской металлической банки, разрезанной по диаметру, с небольшим расстоянием между частями. Они прекрасно видны на патентном рисунке Лоуренса (см. рисунок 6). Дуанты находятся в однородном магнитном поле, линии которого направлены перпендикулярно плоскости дуантов. В центре устройства находится источник ионов, подлежащих ускорению.

Предположим, что ион был послан из источника в глубины дуанта. Там, как в клетке Фарадея, нет электрического поля. Имеется только магнитное поле, под действием которого ион огибает полукруг радиуса r и попадает в область между дуантами, где уже имеется электрическое поле. Вектор напряженности поля E должен быть направлен в соответствии со скоростью положительного иона так, чтобы он ускорялся в зазоре между дуантами.

Ускоренный ион влетает во второй дуант и снова образует полукруг, на этот раз с немного большим радиусом (он движется с большей скоростью) и попадает в зазор между дуантами, где направление электрического поля должно быть изменено на противоположное, так как ион движется в обратном направлении. Как видите, необходим источник переменного напряжения. Символически это показано на рис. 7 в виде прямоугольного сигнала напряжения (обозначено синим).

Рис. 7. Схема конструкции циклотрона с обозначением ионного трека

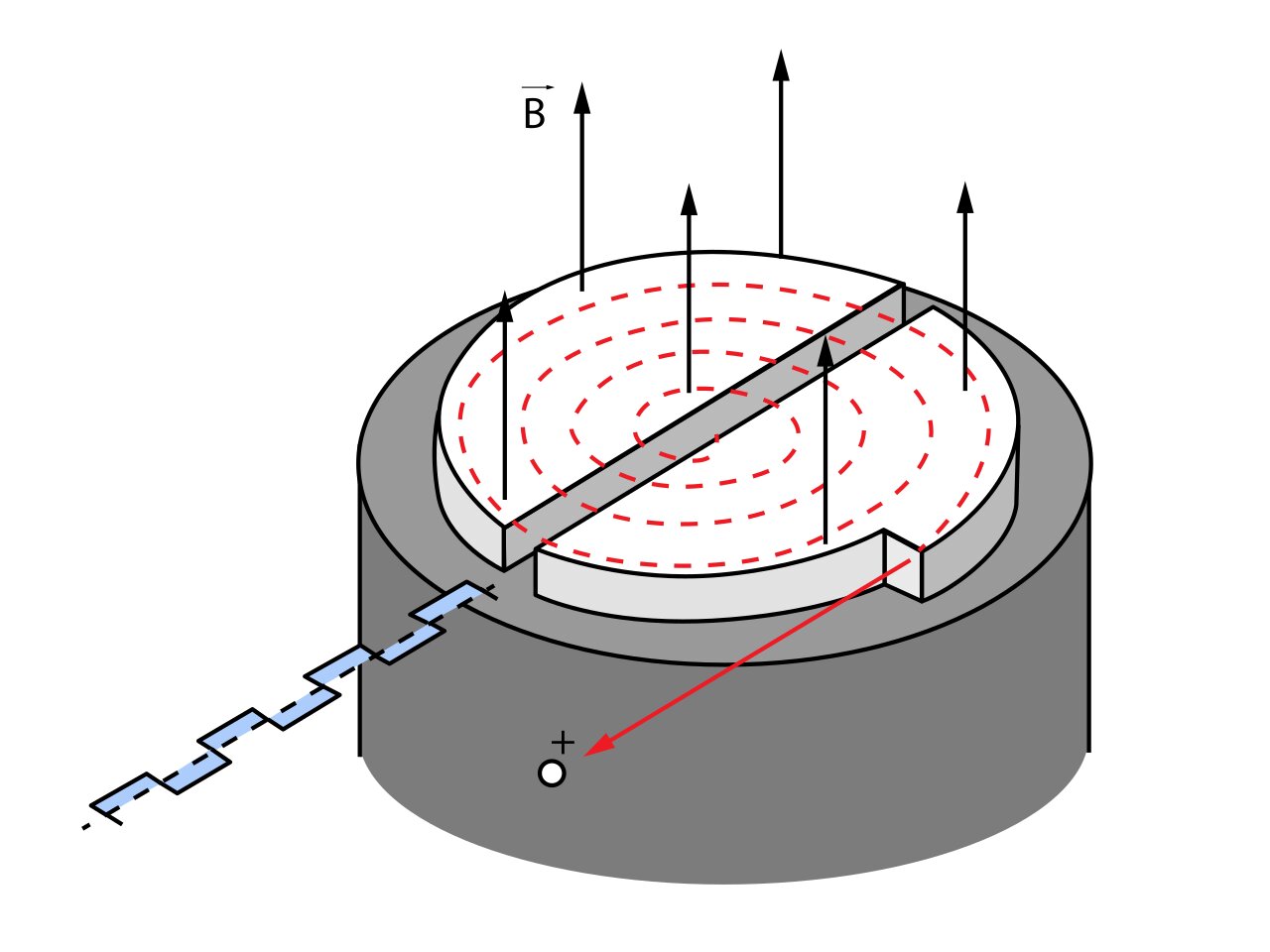
Вычислим радиус полукруга, по которому ион движется внутри дуанта. На ион действует магнитная сила: F_mag = e * v * B * sin∡( v , B ), но ∡( v , B ) = 90° , тогда F_mag = e * v * B .

Магнитная сила всегда действует перпендикулярно вектору скорости и поэтому является центростремительной силой: mv 2 / r = e*v*B , следовательно, радиус можно вычислить так: r = m * v / e * B .

Видео:Урок 278. Задачи на силу Лоренца - 1Скачать

Почему в циклотроне нельзя разогнать частицу до очень большой скорости?

Как мы уже говорили, и как мы заметим, глядя на выведенное соотношение, радиус пути увеличивается со скоростью иона. Но давайте посмотрим, что происходит с периодом вращения иона.

Период вращения иона вычисляется так: T = 2 * π * r / v — потому что мы имеем дело с равномерным движением по окружности (предположим на мгновение, что нарисована полная окружность). Подставим в эту формулу полученную выше зависимость, описывающую радиус пути r.

Получаем: T = ( 2 * π / v ) * ( m * v / e * B ) = 2 * π * m / e * B .

Полученный результат крайне важен для работы циклотрона!

Оказывается, что период вращения иона не зависит от его скорости. Поэтому она одинакова для обеих половин окружности, хотя они имеют разные радиусы. Это значительно упрощает конструкцию циклотрона — приложенное переменное напряжение (которое не обязательно должно быть прямоугольным) имеет постоянную частоту, равную частоте циркуляции ионов. Эта частота называется циклотронной частотой. Она равна обратной величине определяемого периода вращения: f = 1 / T = ( 1 / 2 * π ) * ( e * B / m ) .

Обратите внимание, что здесь мы имеем дело со своего рода резонансом. На рис. 8 показаны соответствующие моменты ускорения иона в щели (зазоре). Вы можете видеть равенство периодов (частот) изменения напряжения и движение по «окружности».

Рис. 8. Слева: траектория частицы в циклотроне с отмеченными моментами наибольшего ускорения. Справа: Временная зависимость напряжения между дуантами

Чтобы определить кинетическую энергию иона, нам не нужно знать, сколько раз он пересекает промежуток между дуантами. Ведь кинетическая энергия связана со скоростью, которая, в свою очередь, связана с радиусом трека ускоренного иона. Давайте посмотрим:

E_k = ( m * v 2 ) / 2 = m / 2 * ( r * e * B / m ) 2 = ( e 2 * B 2 / 2 * m ) * r 2 .

Максимальная энергия будет получена ионом непосредственно перед его выходом из дуанта, поэтому максимальная кинетическая энергия, которая достигается в циклотроне будет вычисляться следующим образом: E_kmax = ( e 2 * B 2 / 2 * m ) * R 2 , где R — радиус циклотронных дуантов.

Ускоритель LHC в ЦЕРНе, упомянутый в начале статьи, очевидно, не является циклотроном. Релятивистские эффекты (скорость протонов сравнима со скоростью света c) приводят к тому, что частота изменения электрического поля непостоянна, но основная идея остается прежней: электрическое поле ускоряет частицы, магнитное поле вызывает их движение по кругу.

Видео:ЕГЭ по физике. Движение заряда в однородном магнитном поле. Теория и задачиСкачать

Синхроциклотрон

Модулируя высокую частоту, вы делаете свой циклотрон пригодным для работы на более высоких скоростях. Для этого вы адаптируете высокую частоту к уменьшающейся частоте циклотрона. Это возможно, например, при использовании вращающегося конденсатора в резонансном контуре. Этот тип циклотрона достигает энергий до 800 МэВ с легкими ионами.

Однако изучать можно только импульсные пучки частиц, т.е. пучки частиц, испускаемые порциями, ограниченными по времени. Это существенный недостаток для большинства экспериментальных применений. Период импульсов луча слишком большой, а сам импульс слишком короткий. В результате многие измерения оказываются невозможными. Отношение длительности импульса к длительности периода также называется рабочим циклом. Для синхроциклотрона (фазотрона) это всего лишь 1%.

Видео:3.405 ИрСкачать

Изохронный циклотрон

Изохронный циклотрон технически более совершенен, чем синхроциклотрон. Вместо модуляции высокой частоты вы поддерживаете орбитальную частоту релятивистских ионов постоянной. Для этого используется неоднородное магнитное поле, которое усиливается наружу. Чтобы сфокусировать пучок частиц, вы настраиваете магнит так, чтобы он имел чередующиеся положительные и отрицательные градиенты в радиальном направлении. Такое разделение на отдельные магниты в форме пирога называется секторным циклотроном.

Сила тока такого изохронного циклотронного пучка составляет от 10 до 100 микроампер.

📸 Видео

Урок 273. Рамка с током в магнитном полеСкачать

Физика: подготовка к ОГЭ и ЕГЭ. Движение заряженных частиц в магнитном полеСкачать