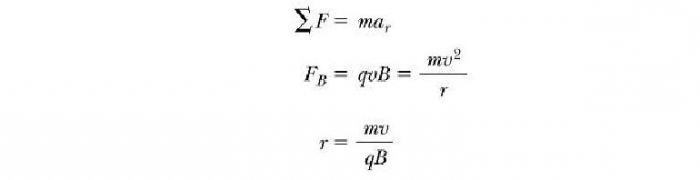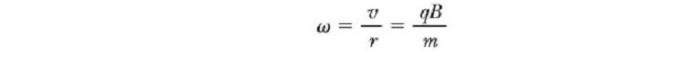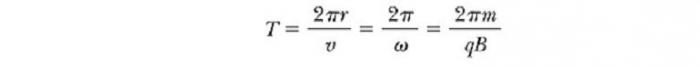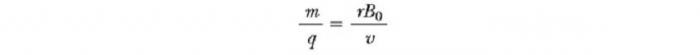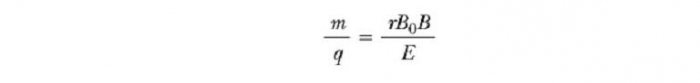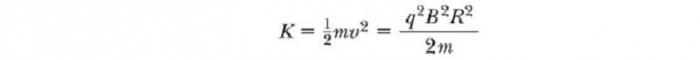Траектория движения электрона в магнитном поле представляет собой окружность

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.

В некоторых электровакуумных приборах используется движение электронов в магнитном поле.

Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.

При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.

Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.

Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.

Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).

Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.

Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.

Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.

Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.

Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.

Видео:Движение электронов в магнитном поле - Сила ЛоренцаСкачать

Рис Влияние магнитного поля на траекторию движения электрона. (Вектор направлен к читателю)

Главная > Документ

Лабораторная работа N 28

ИЗМЕРЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА

Движение электронов в магнетроне

Целью работы является определение удельного заряда электрона методом магнетрона и оценка погрешности его измерения.

Удельный заряд частицы — это отношение ее заряда q к массе m . Простейший магнетрон представляет собой двухэлектродную электронную радиолампу (диод), состоящую из цилиндрического анода и расположенного на его оси катода (рис. 1). Лампа помещается в однородное магнитное поле, направленное по ее оси. В данной работе магнитное поле создается соленоидом (катушкой). Индукция магнитного поля изменяется за счет изменения тока в соленоиде.

Удельный заряд электрона оценивается по экспериментально наблюдаемой зависимости анодного тока врадиолампе от тока в соленоиде: . На электрон, движущийся от катода к аноду, действуют две силы: одна — со стороны электрического поля

, (1)

другая — со стороны магнитного поля – сила Лоренца

. (2)

Первая направлена вдоль радиуса от катода к аноду, вторая — перпендикулярно к векторам скорости и индукции магнитного поля.

Рис.2. Влияние магнитного поля на траекторию движения электрона. (Вектор направлен к читателю)

На рис.2 показаны траектории электронов при различных значениях индукции магнитного поля. По мере увеличения индукции поля траектория электрона все более искривляется и при некотором критическом значении индукции электроны не достигают анода, анодный ток в этот момент резко уменьшается.

Рис.2. Влияние магнитного поля на траекторию движения электрона. (Вектор направлен к читателю)

Изображенную на рис.3(а) и 3(б) зависимость силы анодного тока от индукции магнитного поля называют сбросовой характеристикой магнетрона. График а) соответствует идеальной, б) — реальной характеристикам.

Рис.3. Примерный вид идеальной (а) и реальной

(б) сбросовых характеристик магнетрона

Идеальная характеристика получилась бы при одинаковых скоростях движения электронов в строго однородном поле. Реально прекращение анодного тока происходит не скачком, а плавно. Критическое значение B кр индукции магнитного поля соответствует точке перегиба кривой .

Если радиус катода лампы мал по сравнению с радиусом анода , то электрон ускоряется в основном в пространстве вблизи катода, так как напряженность электрического поля отличается от нуля практически только вблизи катода. Вследствие этого и траектория электрона близка к окружности, а диаметр критической траектории можно считать равным радиусу анода

2. Вывод расчетной формулы

Сила, действующая на электрон со стороны магнитного поля, сообщает ему нормальное ускорение. По второму закону Ньютона

F M = ma n или (4)

. (5)

С другой стороны, известно, что

(6)

где — разность потенциалов между катодом и анодом.

Исключая из (5) и (6) и используя (3), получим формулу для удельного заряда электрона

. (7)

Магнитное поле соленоида конечной длины без сердечника рассчитывается по формуле (см. прил.1).

(8)

где Гн/м — магнитная постоянная; — число витков соленоида; L — его длина; D — диаметр; I c — ток в соленоиде.

Формула для расчета удельного заряда электрона принимает окончательный вид

. (9)

1. В каком случае траектория электрона, движущегося в однородном магнитном поле, представляет собой окружность?

2. При каких условиях траектория электрона, движущегося в скрещенных электрическом и магнитном полях, будет прямолинейной?

3. Заряженная частица прошла ускоряющую разность потенциалов U = 104 В и влетела в скрещенные под прямым углом электрическое ( E = 10 кВ/м) и магнитное ( B = 0,10 Тл) поля. Найти удельный заряд частицы, если, двигаясь перпендикулярно к обоим полям, частица не испытывает отклонения от прямолинейной траектории.

Рис. 4. Схема установки

4. Схема электрической цепи установки

Электрическая цепь установки (рис.4) состоит из двух частей: цепи соленоида (а) и цепи диода (б), в которых: — амперметр для измерения силы тока в соленоиде; — микроамперметр для измерения силы анодного тока; — вольтметр для измерения анодного напряжения; П 1 и П 2 — регуляторы тока и напряжения.

5. Порядок выполнения работы

В лаборатории физического практикума кафедры физики УГТУ-УПИ смонтирован магнетрон, изображенный на фотографии на титульном файле данной работы, при этом используется обычная радиолампа (диод), помещенная в относительно длинный соленоид, создающий достаточно однородное магнитное поле, что позволяет применять вышеописанную методику измерения и расчета удельного заряда электрона.

В компьютерном варианте данной работы максимально точно моделируются условия проведения эксперимента, на экране дисплея воспроизводятся миллиамперметр, измеряющий ток соленоида, и микроамперметр, регистрирующий анодный ток в радиолампе, что позволяет практически построить сбросовую характеристику магнетрона.

При этом от экспериментатора требуется аккуратность в проведении опыта и правильность записи результатов измерений, обработки опытных данных, расчета искомой величины и погрешности результата измерений. Измерения можно проводить как при монотонном повышении тока соленоида, так и при его уменьшении. Работать следует только с клавиатурой и мышкой.

Однако прежде чем выполнять экспериментальную часть работы, следует внимательно прочитать теоретическую часть данного руководства и ответить на контрольные вопросы.

Навести курсор на «Измерения», нажать левую клавишу мышки. При этом на дисплее Вашего компьютера появится миллиамперметр и микроамперметр, регистрирующие токи соленоида и радиолампы, соответственно.

2. Ознакомиться с приборами и заполнить таблицу «Средства измерений и их характеристики» отчета (смотри ниже Приложение 2).

3.Записать в отчет данные о параметрах магнетрона. Измерения проводятся при анодном напряжение U a =6,0+_0,1В.

4.Навести курсор на регулятор тока соленоида, постепенно повышая значения тока в соленоиде снять зависимость анодного тока от силы тока I c в соленоиде. Рекомендуется снять 18 точек. Результаты измерений внести в таблицу 2 отчета. По экспериментальным данным построить на миллиметровой бумаге график .

5. По полученным данным определить критическое значение тока в соленоиде I C, кр методом графического дифференцирования зависимости , которое осуществляется следующим образом. По парам ближайших точек тока соленоида (таблица 2) найти , и и занести эти результаты в таблицу 3. Построить на миллиметровой бумаге график зависимости , где есть среднее значение тока двух соседних точек, т.е. на оси абсцисс значение тока соленоида брать между двумя соседними точками. Точку на оси абсцисс, соответствующую максимуму графика принять за I С, кр .

6. Рассчитать удельный заряд электрона по основной расчетной формуле. Сравнить полученный результат с табличным значением удельного заряда электрона.

7. Рассчитать границу относительной и абсолютной погрешности результата измерения удельного заряда электрона по формуле, приведенной в отчете. В случае значительного расхождения опытных и табличных значений повторить измерения.

8. Оформить отчет (см. Приложение 2) и сдать его преподавателю на проверку.

Индукция поля соленоида без сердечника на его оси может быть найдена по формуле

(П.1.1)

где — общее число витков соленоида, — сила тока в соленоиде, — его дли

на, и — углы между осью соленоида и радиусами -векторами, проведенными от его середины к крайним виткам (см. рисунок).

Из рисунка видно, что

Таким образом, имеем

К расчету индукции магнитного поля соленоида

(П.1.2)

Если (соленоид длинный), то

по лабораторной работе № 28

“ Измерение удельного заряда электрона методом магнетрона”

На внутренних страницах:

1. Основная расчетная формула для определения удельного заряда электрона (пояснить смысл входящих в нее величин).

2. Средства измерений и их характеристики.

Погрешности,

3. Параметры соленоида и диода.

а) Соленоид: диаметр = 33,5 мм, длина =50 мм,

число витков = 1870; = 0,5мм, = 1 мм;

б) диод — радиус анода =5,0 мм, = 0,1 мм.

в) Анодное напряжение принять равным 6,0В +_ 0,1В.

б) =. А (принимается равным половине интервала приращения тока соленоида вблизи критической точки).

4. Схема электрической цепи.

5. Результаты измерений (в форме таблиц 2 и 3).

Зависимость анодного тока от тока в соленоиде

6. Построение графика

7. Определение критического тока I c,кр в соленоиде по графику, построенному по данным таблицы 3.

мкА

,мА

8. Удельный заряд электрона

, Кл/кг

9. Оценка границы погрешности результата измерения

Кл/кг. Округлить до одной значащей цифры.

10. Окончательный результат Кл/кг. Округлить результат измерения, согласовав разряд последней значащей цифры с разрядом погрешности измерения.

11.Выводы по работе (сравнить полученный результат с табличным значением измеряемой величины, проанализировать погрешности и т.д.).

Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Видео:Физика - Магнитное полеСкачать

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Видео:Движение заряженной частицы в магнитном поле 2021-1Скачать

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Видео:Движение электрона в магнитном поле.Скачать

Движение заряженных частиц в однородном магнитном поле

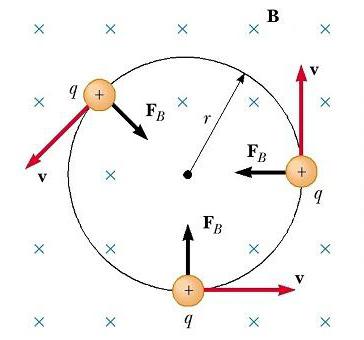
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Видео:Движение заряженных частиц Лекция 9-2Скачать

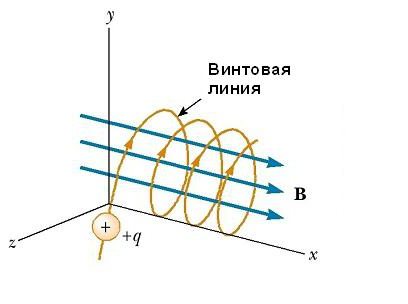
Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Видео:Теория движения заряженных частиц в электрическом поле .Часть 1Скачать

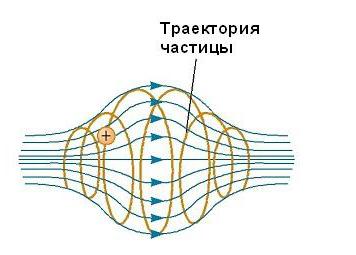
Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Видео:Электрон в магнитном полеСкачать

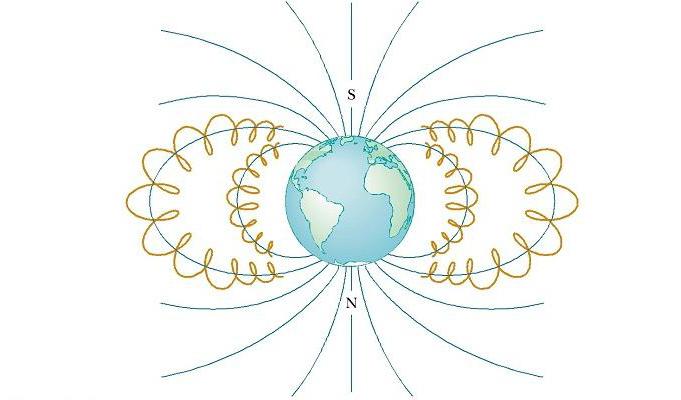
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Видео:Тема 27. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

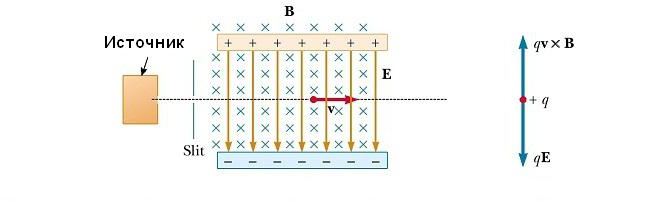
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Видео:Движение заряда по спирали в магнитном полеСкачать

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Видео:Движение свободных электронов в металлахСкачать

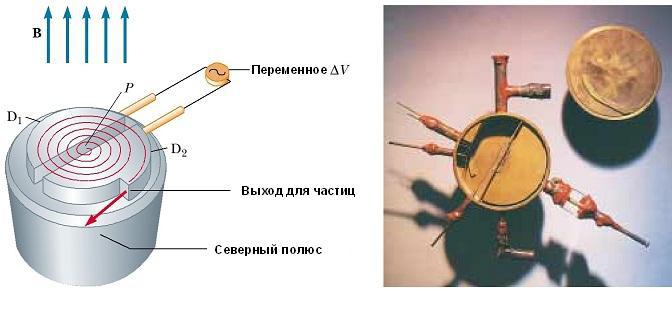
Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Видео:Пучок электронов в магнитном полеСкачать

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

📽️ Видео

Парфенов К.В. - Олимпиадная физика для 11-го класса - 9. Движение зарядов в магнитном полеСкачать

МАГНИТНОЕ ПОЛЕ за 24 минуты. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

Движение электронов в атоме. 1 часть. 8 класс.Скачать

Магнитное поле движущихся зарядов 1980 гСкачать

ГАРОЛЬД ГУРЕВИЧ. Лекция: "Траектория движения микрочастиц вещества"Скачать

Физика Электрон влетает в однородное магнитное поле со скоростью 10000 км/с и движется по окружностиСкачать