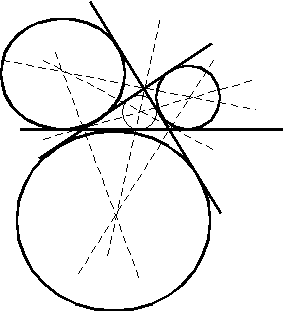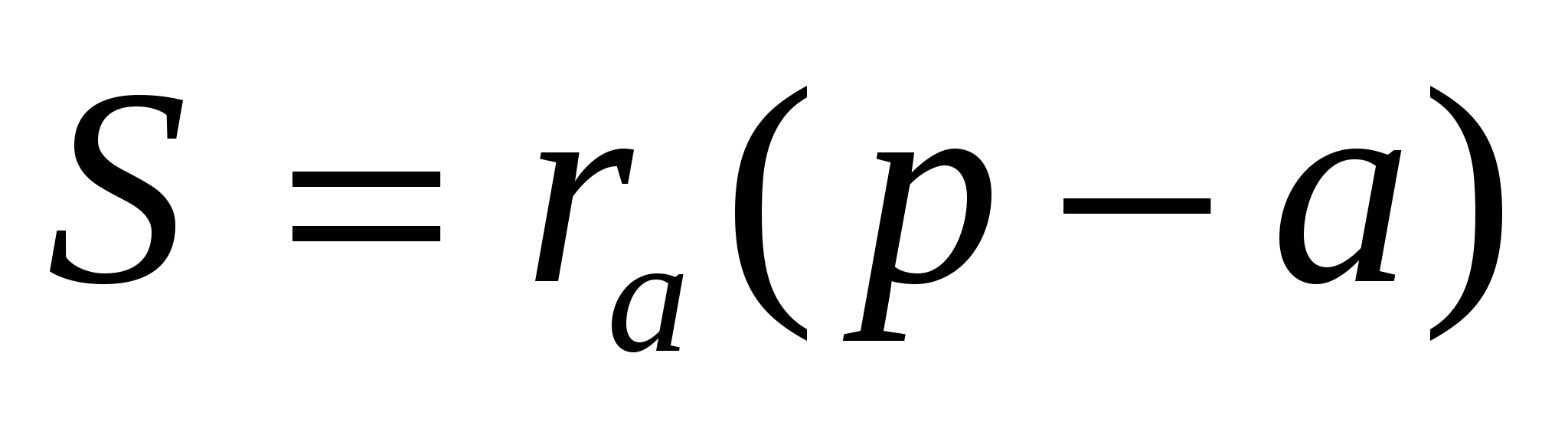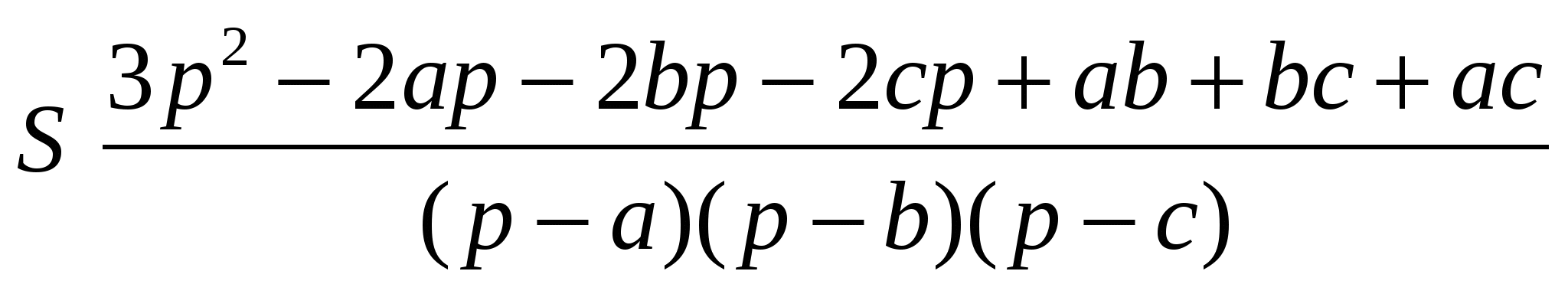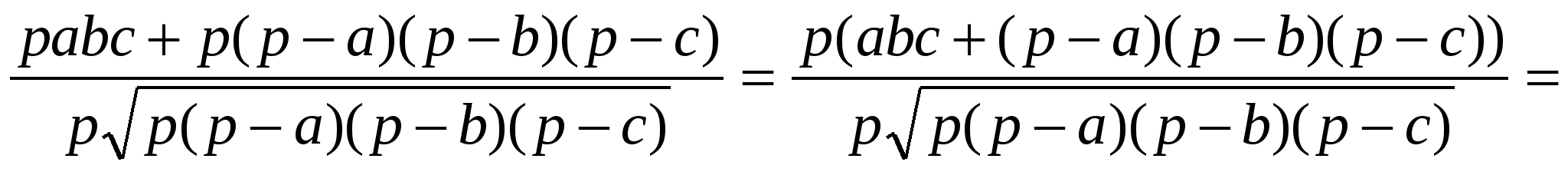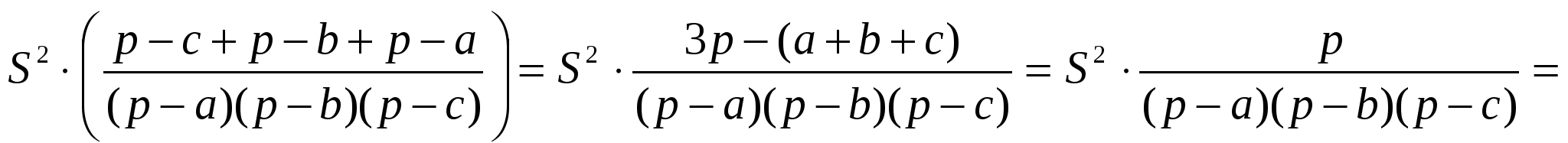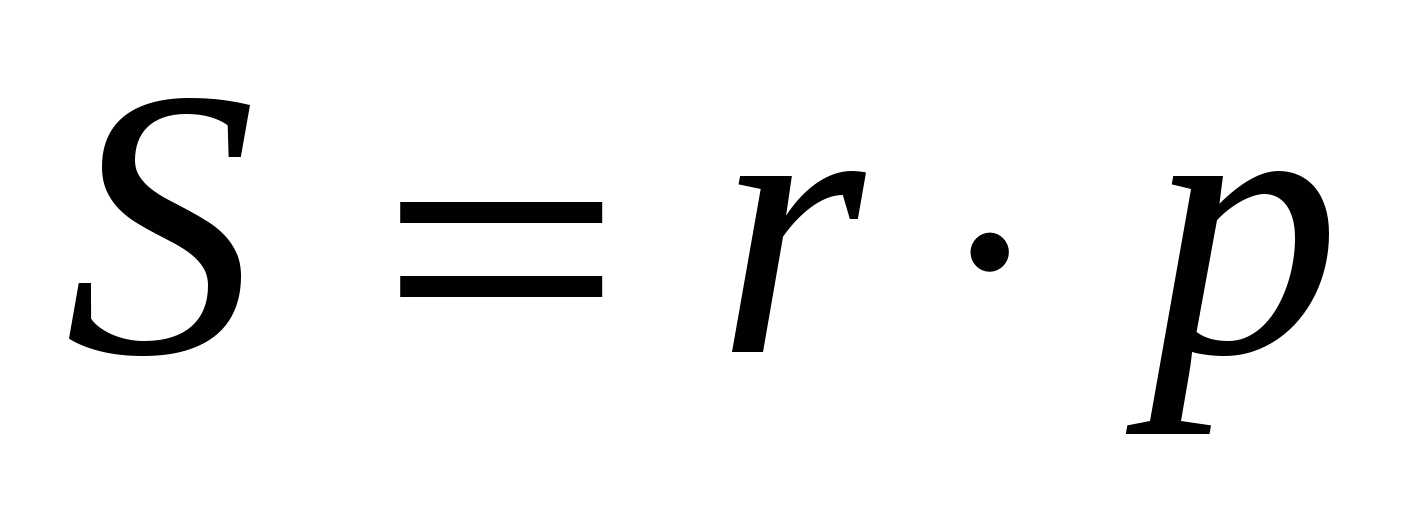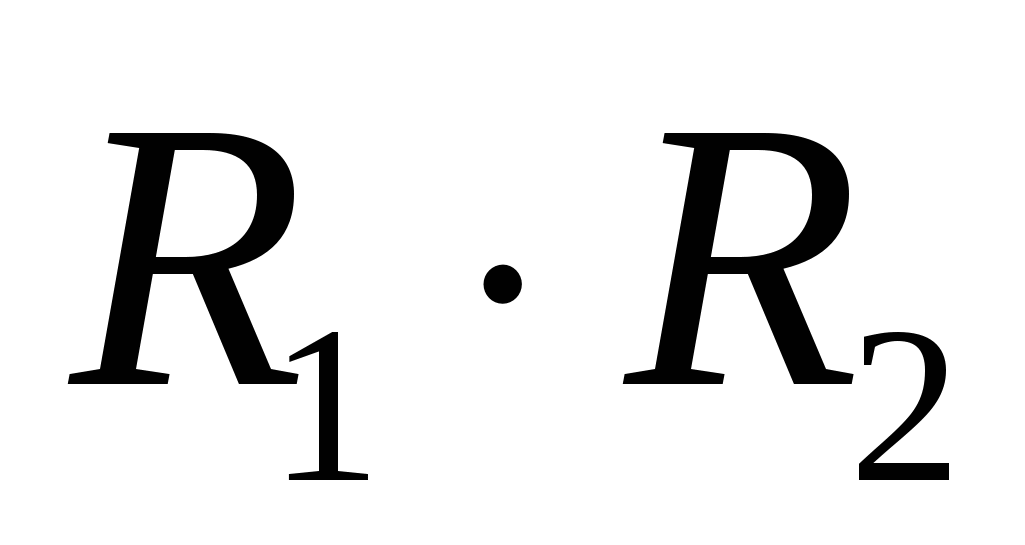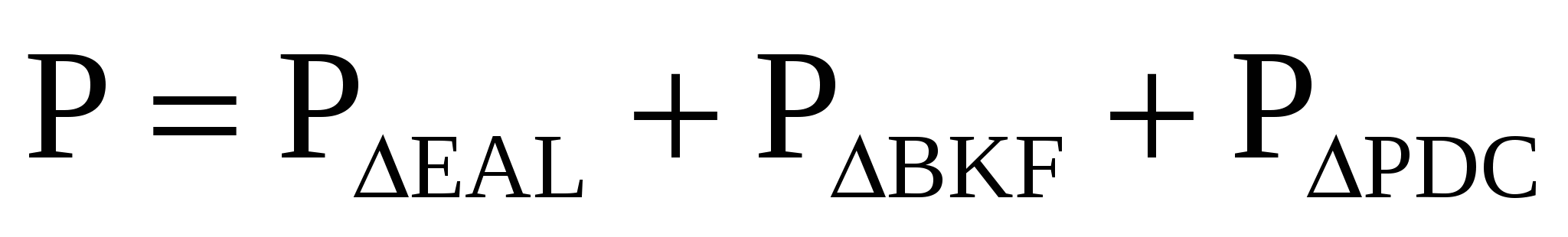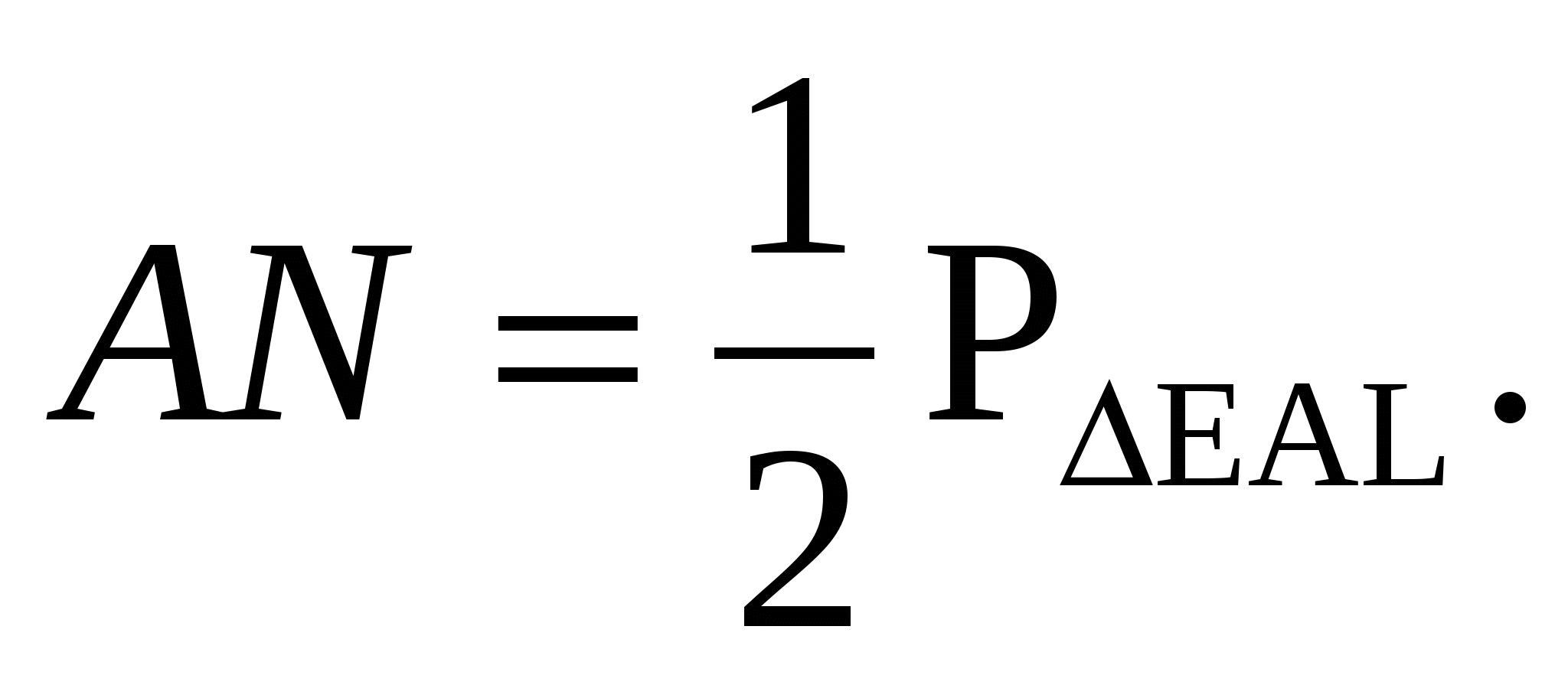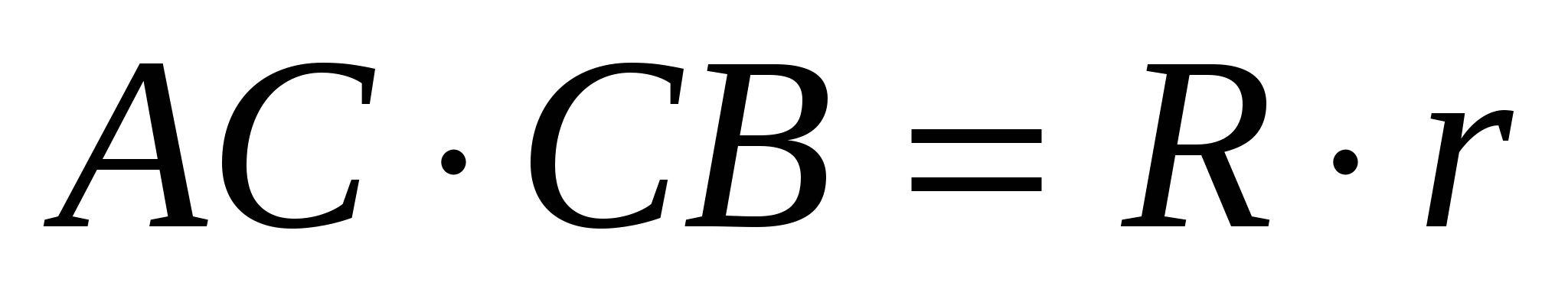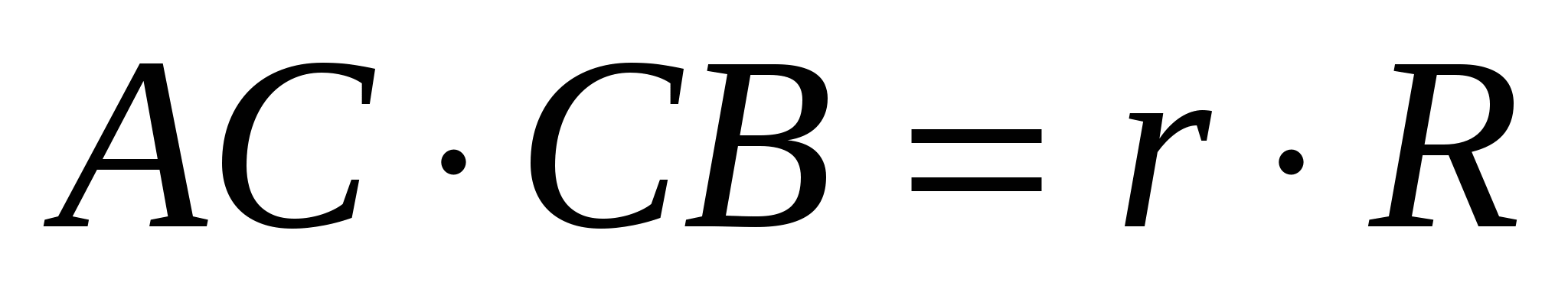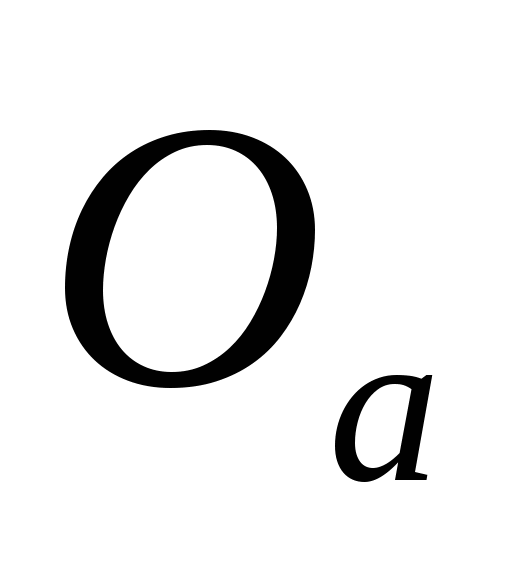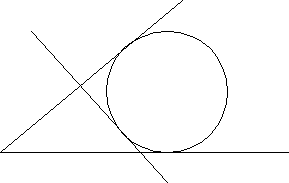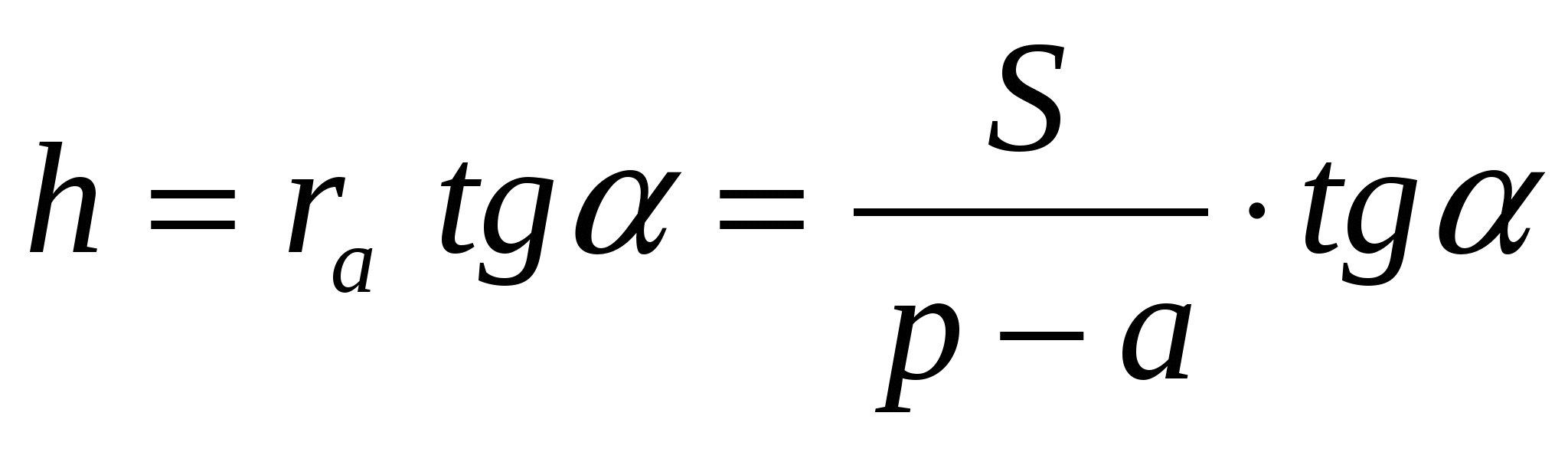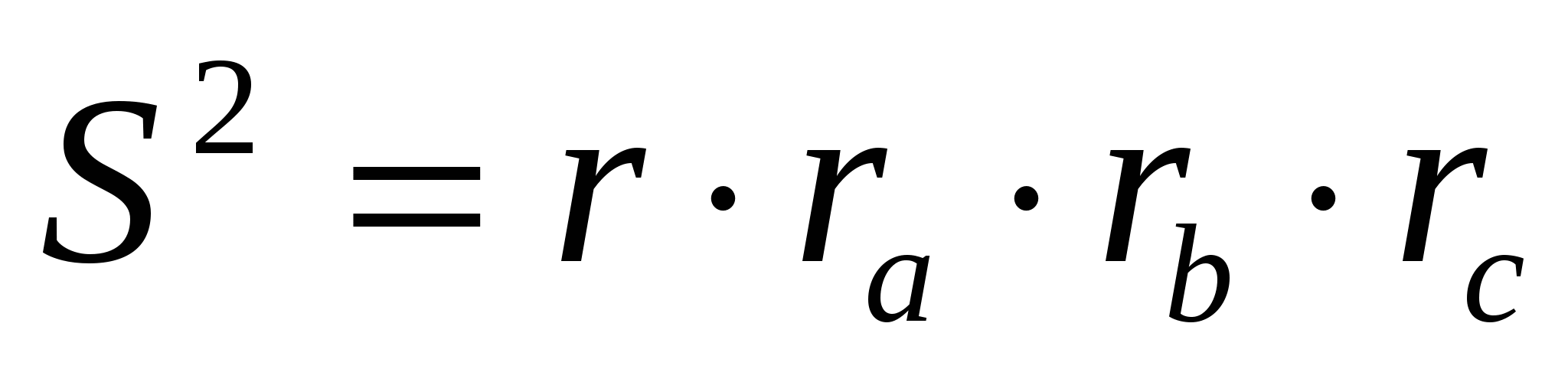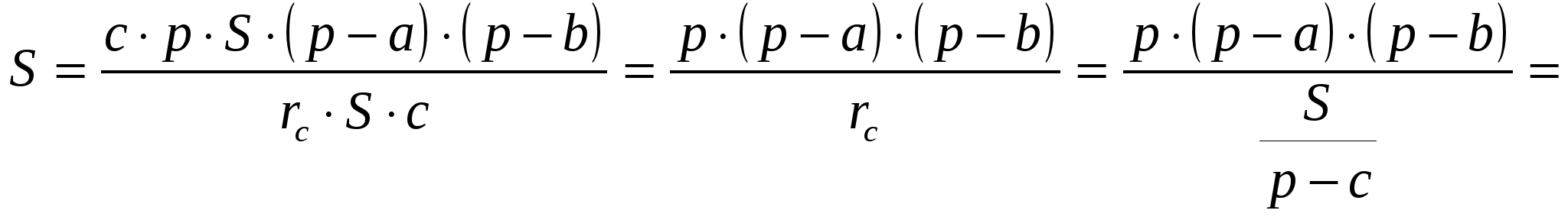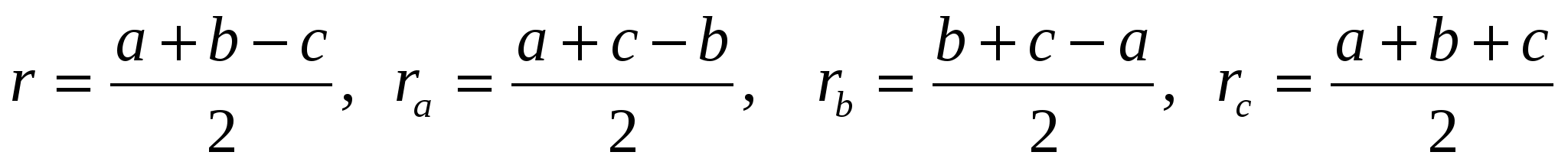Точки ia и ic центры вневписанных окружностей треугольника abc

Решение более сложных задач для 9 класса. Рассмотрены задачи из планиметрии.

Просмотр содержимого документа
«Геометрия в 9-ом классе»

Геометрия в 9-ом классе

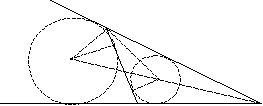
Дана окружность ω радиуса r=8. Прямая aa, проходящая через точку A, лежащую вне окружности ω, пересекает окружность ω в точках B и C. Известно, что AB=4, AC=9.

По теореме о секущей и касательной AK 2 =AB⋅AC, откуда AK=AB⋅AC=√4⋅9=6.

Степень точки A равна AB⋅AC=AO2−r2. Отсюда AO2=r2+AB⋅AC=64+36=100, следовательно, AO=10.

Сторону AB треугольника ABC продолжили за вершину B и выбрали на луче AB точку A1 так, что точка B — середина отрезка AA1 . Сторону BC продолжили за вершину C и отметили на продолжении точку B1 так, что C — середина BB1. Аналогично, продолжили сторону CA за вершину A и отметили на продолжении точку C1 так, что A – середина CC1. Найдите площадь треугольника A1B1C1, если площадь треугольника ABC равна 1.

Соединим точки A и B1, B и C1, C и A1 отрезками. Полученные отрезки являются медианами в треугольниках C1CB1, A1AC1, B1BA1 соответственно. Отсюда следует, что SBC1A=SBC1A1, SCA1B=SCA1B1, SAB1C=SAB1C1.

Заметим, что отрезки BA, CB, AC — медианы в треугольниках CBC1, ACA1, BAB1 соответственно. Отсюда (по свойству медианы, а также из сказанного ранее) вытекает, что SABC=SABC1=SBC1A1, SABC=SAB1C=SAB1C1.

Таким образом, мы доказали, что все маленькие треугольники, на которые разбит треугольник A1B1C1, имеют равную площадь, причем она равна 1, поскольку один из этих треугольников есть треугольник ABC. Всего маленьких треугольников ровно 7, значит, площадь треугольника A1B1C1 равна 7.

Вершины A, B, C и D параллелограмма ABCD соединили с серединами сторон BC, CD, DA и AB (обозначим эти точки через A1, B1, C1 и D1) соответственно. Найдите площадь ограниченного этими прямыми четырехугольника, если SABCD=10.

Введем следующие обозначения: K — пересечение AA1 и BB1, P — пересечение BB1 и CC1, L — пересечение CC1 и DD1 M — пересечение DD1 и AA1. Заметим, что четырехугольник KPLM параллелограмм, поскольку AA1∥CC1, BB1∥DD1.

Высоты BH1 и СH2, опущенные из точек B и C на прямую AA1, одинаковы, поскольку прямоугольные треугольники BH1A1 и CH2A1 равны по гипотенузе (BA1=A1C) и острому углу.

Заметим, что AK=2MK, это вытекает из теоремы Фалеса, поскольку AB=2AD1, а прямые BB1∥DD1. Отсюда следует, что AM=MK. Аналогично получаем, что BK=KP, CP=PL, DL=LM.

Из выше сказанного следует, что SABK=SKPLM. Действительно, SABK=12BH1⋅AK=BH1⋅MK=CH2⋅MK, а поскольку CH2 — расстояние между параллельными прямыми AA1 и CC1, то CH2 равно высоте параллелограмма, откуда получается, что CH2⋅MK=SKPLM.

Аналогично получается, что SABK=SBCP=SCDL=SDAM=SKPLM. Все эти равные площади вместе дают площадь параллелограмма ABCD. То есть 5SKPLM=SABCD, поэтому SKPLM=2.

Прямая, соединяющая центр описанной окружности и ортоцентр неравнобедренного треугольника, параллельна биссектрисе одного из его углов. Чему равен этот угол?

Без ограничения общности можно считать, что биссектриса угла C треугольника ABC параллельная прямой Эйлера HO (все обозначения стандартны). Пусть C1 — середина отрезка AB, а точка C0 — середина дуги AB, иными словами, вторая точка пересечения биссектрисы угла C с описанной окружностью треугольника ABC. Пусть CK — высота из точки C на прямую AB. Заметим, что прямые OC0 и CH параллельны, так как обе перпендикулярны прямой AB. Если точка H находится между точек C и K, или KK между C и H, то точки O и H будут находиться по разные стороны относительно прямой CC0, а это противоречит условию задачи. Поэтому точка C находится между точками H и K, что значит, что ∠С90∘.

Заметим, что четырехугольник OC0CH — параллелограмм (его стороны попарно параллельны), тогда CH=OC0=R, где R — радиус описанной окружности. Известно, что CH=2OC1, поэтому легко видеть, что в прямоугольном треугольнике OC1B катет OC1 равен половине гипотенузы OB=R, значит, ∠BOC1=60∘. Это половина центрального угла AOB, тогда вписанный угол AC0B равен 60∘, а угол C дополняет его до 180∘, то есть ∠C=180∘−60∘=120∘.

Отрезки, соединяющие основания высот остроугольного треугольника ABC, равны 5, 12 и 13. Найдите радиус описанной около треугольника ABC окружности.

Заметим, что треугольник с вершинами в основаниях высот прямоугольный (следует из теоремы Пифагора). Пусть его вершины A1, B1, C1 напротив точек A, B, C соответственно, причем A1C1=13. Тогда A1BC1 подобен треугольнику ABC, причем коэффициент подобия равен cos∠B. Известно, что отрезки, соединяющие основания высот, входят в эти точки под равными углами, причем равными соответствующим углам треугольника, то есть, в данном случае ∠AB1C1=∠CB1A1=∠B, а поскольку ∠A1B1C1=90∘, то оба уголка при вершине B1 равны по 45∘, откуда следует, что ∠B=45∘. Таким образом, AC=A1C1cos∠B=132–√AC=A1C1cos⁡∠B=132. Радиус описанной окружности треугольника ABCABC легко находится по теореме синусов: R=AC2sin∠B=132–√⋅2–√2=13R=AC2sin⁡∠B=132⋅22=13.

Внутри параллелограмма ABCDABCD взята точка OO так, что ∠OAD=∠OCD. Известно, что ∠BAD=75∘, ∠OBA=65∘, найдите градусную меру ∠ODC.

Если сделать параллельный перенос всей картинки на вектор AD→, то при этом преобразовании точка CCперейдет в точку C′, D — в точку D′

. Ясно, что точка A перейдет в точку D, а точка B перейдет в C.

Ясно, что ∠OAD = ∠O′DD′. Нетрудно заметить, что ∠OO′D=∠O′DD′, как накрест лежащие углы при параллельных прямых OO′′ и DD′′. Отсюда следует, что ∠OCD=∠OAD=∠O′DD′=∠OO′D, значит четырехугольник OCO′D — вписанный.

Отсюда можно получить, что ∠ODC=∠OO′C, который из аналогичных предыдущему рассуждений равен ∠O′CC′=∠OBC. Остается просто посчитать. Ясно, что

Пусть IA, IB, IC — центры вневписанных окружностей треугольника ABC, касающихся сторон BC, AC, AB соответственно. Известно, что BC=5√3, ∠A=60∘. Найдите радиус описанной окружности треугольника IAIBIC.

Рассмотрим точки A1, B1, C1 — пересечения с описанной окружностью треугольника ABC биссектрис его углов при вершинах A, B, C. Из обобщенной леммы о трезубце следует, что IA1=IAA1, IB1=IBB1, IC1=ICC1, где I — центр вписанной окружности треугольника ABC.

Заметим, что при гомотетии с центром в точке II и коэффициентом k=2точки A1, B1, C1 переходят в точки IA, IB, IC.

Таким образом, получается, что радиус описанной окружности треугольника IAIBIC равен удвоенному радиусу описанной окружности треугольника A1B1C1, которая совпадает с описанной окружностью треугольника ABC.

Ее радиус легко находится по теореме синусов в треугольнике ABC. Имеем

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вневписанная окружность треугольника.

Определение.

Окружность, касающаяся стороны треугольника и продолжения двух других его сторон, называется вневписанной окружностью треугольника.

Теорема 1.

Центр окружности, вневписанной в треугольник, есть точка пересечения биссектрис двух внешних и одного внутреннего угла треугольника.

Доказательство.

BF — биссектриса ∠JBG, следовательно F равноудалена от сторон данного угла.

СF — биссектриса ∠JСH, следовательно F равноудалена от сторон данного угла.

Следовательно, точка F равноудалена от сторон ∠BAC.

Таким образом, точка F — центр окружности, касающейся стороны BC и продолжения сторон AB и AC. По определению данная окружность называется вневписанной окружностью треугольника.

Теорема 2.

Отрезок, соединяющий вершину треугольника с точкой касания вневписанной окружности и противолежащей стороны, делит треугольник на два треугольника равного периметра.

Доказательство.

BJ=BG, GC=CH и AJ=AH (свойство отрезков касательных, проведенных из одной точки к окружности).

P_ΔABC=AB+ BC +AC=AB+ BG + GC +AC=AB+ BJ + AC +CH=AJ+AH.

Так как AJ=AH, то P_ΔABC/2=AJ=AH и P_ΔABC/2+AG=AJ+AG=AH+AG=AB+BG+GA=AC+CG+GA.

Следовательно, отрезок AG поделил треугольник ABC на два треугольника равного периметра P_ΔABC/2+AG.

Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Вневписанная окружность (8 — 9 класс)

Методическая разработка по геометрии «Вневписанная окружность».

Литвинова Светлана Александровна,

учитель высшей квалификационной категории

МОУ гимназии № 7 г. Волгограда,

Тараева Галина Юрьевна,

учитель высшей квалификационной категории

МОУ гимназии № 7 г. Волгограда.

Действующие школьные программы по математике не предусматривают изучение понятия вневписанной окружности треугольника. Однако с ним полезно ознакомиться, так как решение некоторых типов геометрических задач, и, прежде всего задач на построение, связано с использованием этого понятия.

Вневписанная окружность представляется изысканным элементом геометрии треугольника. А вот знакомство с ней зачастую ограничивается определением, нахождением ее центра и решением нескольких популярных задач, встречающихся на конкурсных экзаменах. Но при более подробном знакомстве с вневписанной окружностью можно увидеть в ней скрытую красоту и силу.

Простейший из многоугольников – треугольник – играет в геометрии особую роль. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.

Первые упоминания о треугольнике и его свойствах мы находим в египетских папирусах, которым более 4000 лет. Через 2000 лет в Древней Греции изучение свойств треугольника достигает высокого уровня – достаточно вспомнить теорему Пифагора и формулу Герона.

Центральное место в геометрии треугольника занимают свойства так называемых замечательных точек и линий.

Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке – центре описанной около треугольника окружности.

Биссектрисы трех внутренних углов треугольника пересекаются в одной точке – центре вписанной в треугольник окружности.

Если рассмотреть дополнительно биссектрисы трех пар внешних углов треугольника, то получаются еще три замечательных точки – центры вневписанных окружностей.

В XV — XVI веках появилось огромное количество исследований свойств треугольника. Эти исследования составили большой раздел планиметрии, получивший название «Новая геометрия треугольника». Вот одна из замечательных теорем того времени, принадлежащая Л. Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения лежат на одной окружности». Она обычно называется окружностью девяти точек (по количеству замечательных точек, через которые она проходит).

У каждого треугольника имеется, и притом только единственная, окружность девяти точек. Это – окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника (рис.1): основания его высот D₁, D₂, и D_3,, основания его медиан D₄, D ₅ и D ₆, середины D₇, D₈ и D₉ отрезков прямых от точки пересечения его высот H до его вершин.

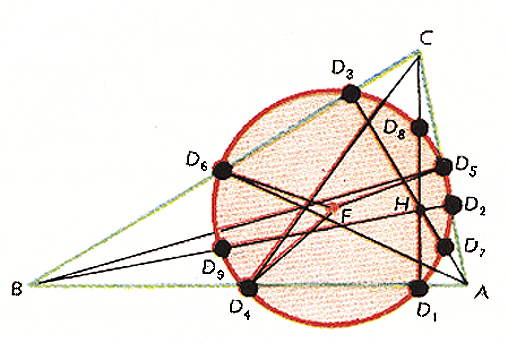
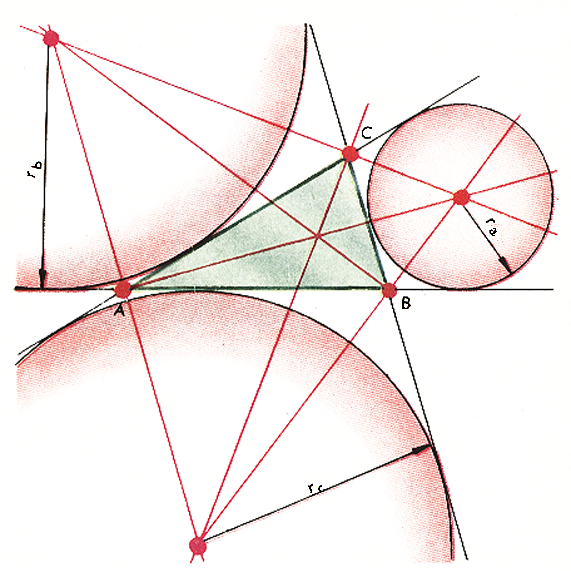
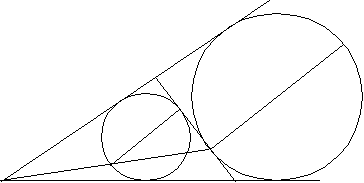
Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта немецким математиком XIX века К. Фейербахом (братом известного философа).

Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это – точки ее касания с четырьмя окружностями. Одна из этих окружностей вписанная, остальные три – вневписанные (рис.2).

Т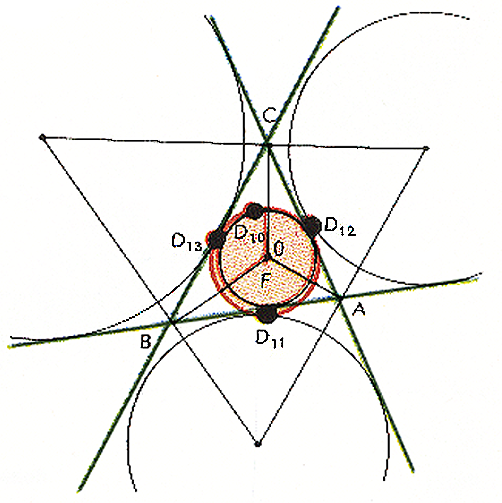очки касания этих окружностей с окружностью девяти точек D₁₀ , D₁₁ , D₁₂ и D₁₃ называются точками Фейербаха. Таким образом, окружность девяти точек в действительности является окружностью тринадцати точек.

Рис.3.

Прямые в треугольнике, соединяющие его вершины с точками касания вневписанных окружностей, пересекаются в одной точке (рис.3), которая называется точкой Нагеля в честь открывшего ее немецкого математика Августа Нагеля (1821-1903).

I . Вневписанная окружность и ее свойства

1. Задачи, приводящие к понятию вневписанной окружности

В курсе геометрии 8-го класса при изучении темы «Вписанная и описанная окружности» предлагается вписать окружность в произвольный треугольник. Решение данной задачи однозначно. Но стоит изменить условие следующим образом «Построить окружность, касающуюся трех данных несовпадающих прямых AB, BC и CA», как однозначность решения пропадает.

Выясним, какие вообще бывают окружности, касающиеся трех данных прямых.

Так как прямые не совпадают, то точки А, В и С не лежат на одной прямой. Центр окружности, касающейся двух прямых, лежит на биссектрисах углов, полученных при пересечении этих прямых (рис.4).

Р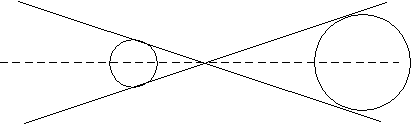ис.4.

Поэтому центры окружностей, касающихся прямых AB, BC и CA лежат на биссектрисах внешних или внутренних углов треугольника (или же на их продолжениях) (рис.5).

В итоге получаем четыре окружности с центрами О, О_а, О_b, О_с, касающиеся трех данных несовпадающих прямых. При этом одна из них будет вписанной в треугольник окружностью, а три других — вневписанными окружностями.

Существует еще одна проблема, приводящая к понятию вневписанной окружности. Нетрудно с помощью циркуля и линейки построить треугольник по его сторонам. Чуть труднее сделать это по медианам или высотам. А вот построить треугольник по биссектрисам (в общем случае) невозможно. Если провести все три биссектрисы внешних углов треугольника, то образуются три точки их пересечения. Каждая из этих точек одинаково отстоит от прямых, содержащих стороны данного треугольника. Поэтому можно провести окружность с центром в такой точке, касающуюся всех сторон треугольника или их продолжений. Такие окружности и будут вневписанными.

2. Определение вневписанной окружности, ее центр и радиус

Дадим определение вневписанной окружности.

Определение: Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.

Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных.

Центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.

Доказательство этого следует из основного свойства биссектрисы угла: все точки, лежащие на ней равноудалены от сторон угла.

С другой стороны, центр вневписанной окружности лежит на пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.

Данное свойство вытекает из следующей теоремы.

Теорема 1. Биссектриса внутреннего угла ВАС треугольника АВС и биссектрисы двух внешних углов при вершинах В и С пересекаются в одной точке.

Доказательство. Проведем внешние биссектрисы из вершин В и С. Пусть они пересекаются в точке О_а. Докажем, что биссектриса угла ВАС проходит через точку О_а. Все точки биссектрисы СО_а равноудалены от сторон угла, значит, расстояние от точки О_а до прямых ВС и АС равны, так как О_а лежит на биссектрисе угла ВСК₁, то есть О_аК₁ = О_аК₃.

ис.7. Аналогично, равны расстояния от точки О_а до прямых ВС и АВ — О_аК₂ = О_аК₃ . Тогда очевидно, что точка О_а равноудалена от прямых АС и АВ, то есть лежит на биссектрисе угла ВАС.

Из теоремы 1 следует существование окружности с центром в точке О_а, касающейся прямых АС, АВ и ВС. Данную окружность и называют вневписанной окружностью.

Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырех точках – центрах вписанной и трех вневписанных окружностей.

Радиусом вневписанной окружности является отрезок перпендикуляра, проведенного из центра окружности к какой-либо стороне треугольника или ее продолжению.

3. Свойства вневписанной окружности и её связь с основными элементами треугольника

Теорема 2. Пусть К₁ – точка касания вневписанной окружности с продолжением стороны АС треугольника АВС. Тогда длина отрезка АК₁ равна полупериметру треугольника АВС.

Из курса планиметрии известны формулы, устанавливающие связи между сторонами треугольника, его площадью и радиусами вписанной и описанной окружностей, . Существует аналогичная связь и с радиусами вневписанных окружностей.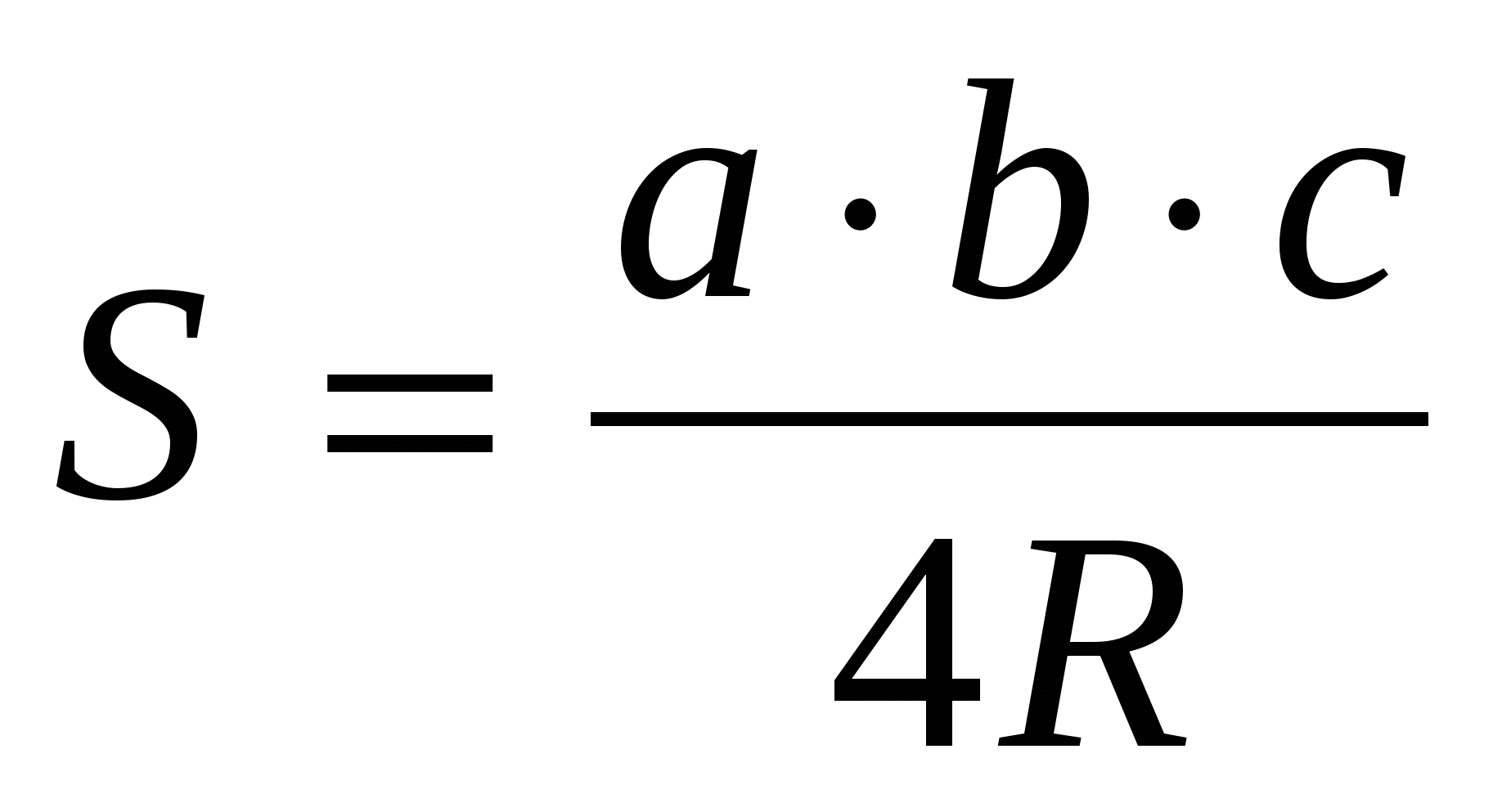

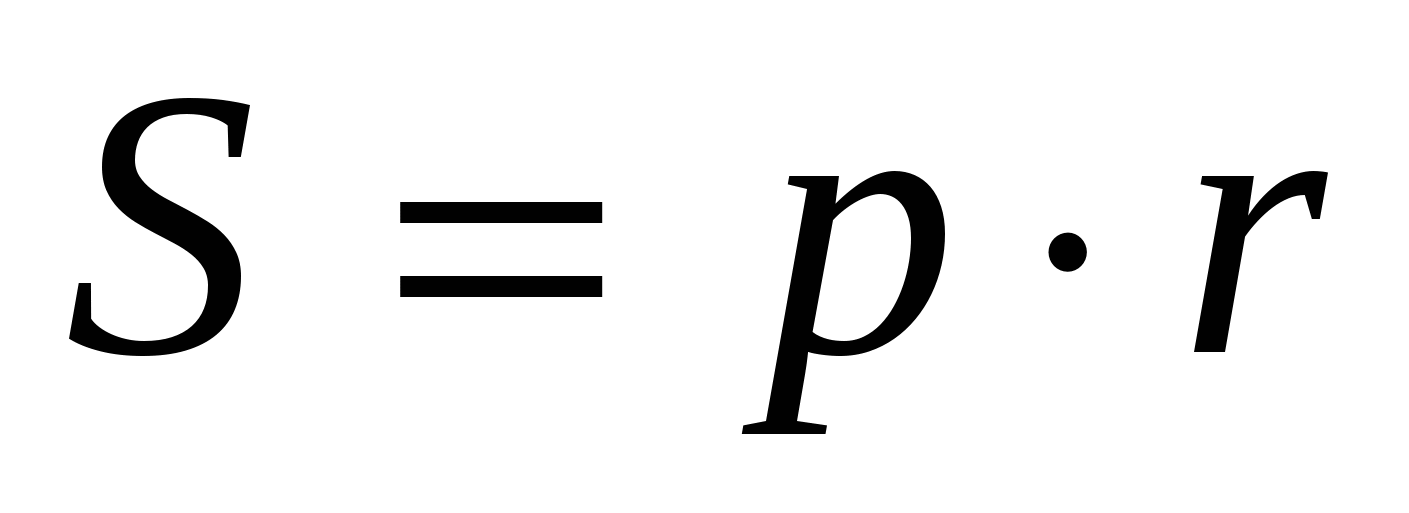
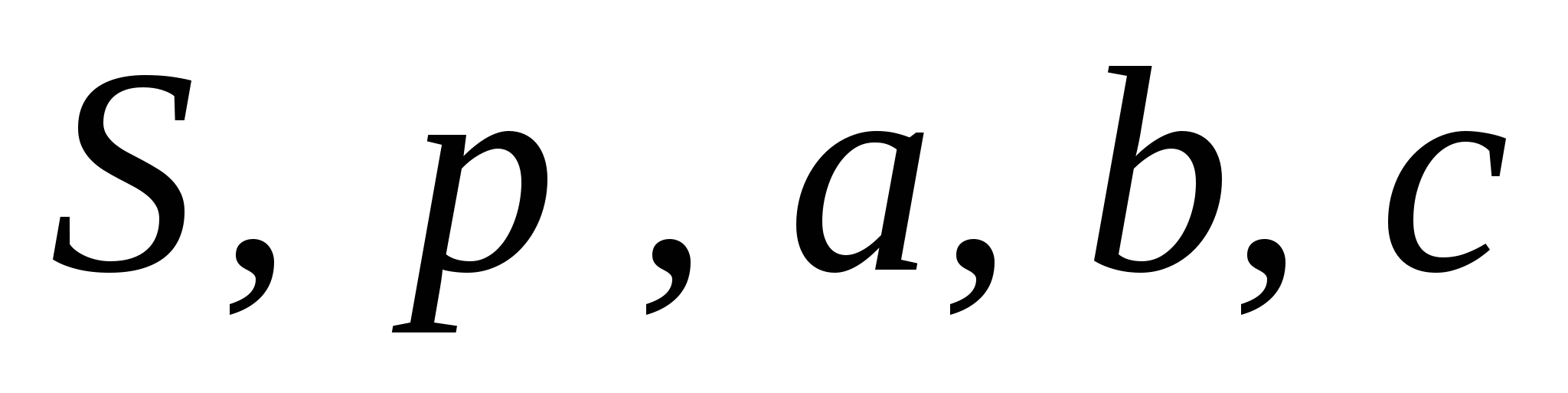
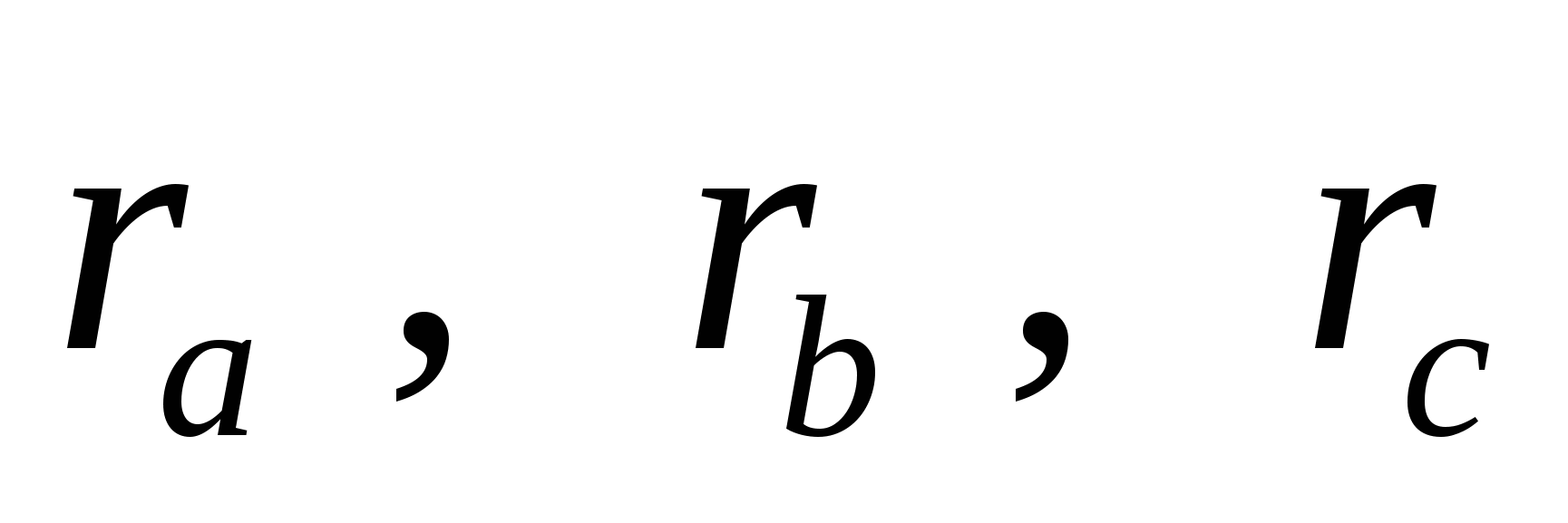
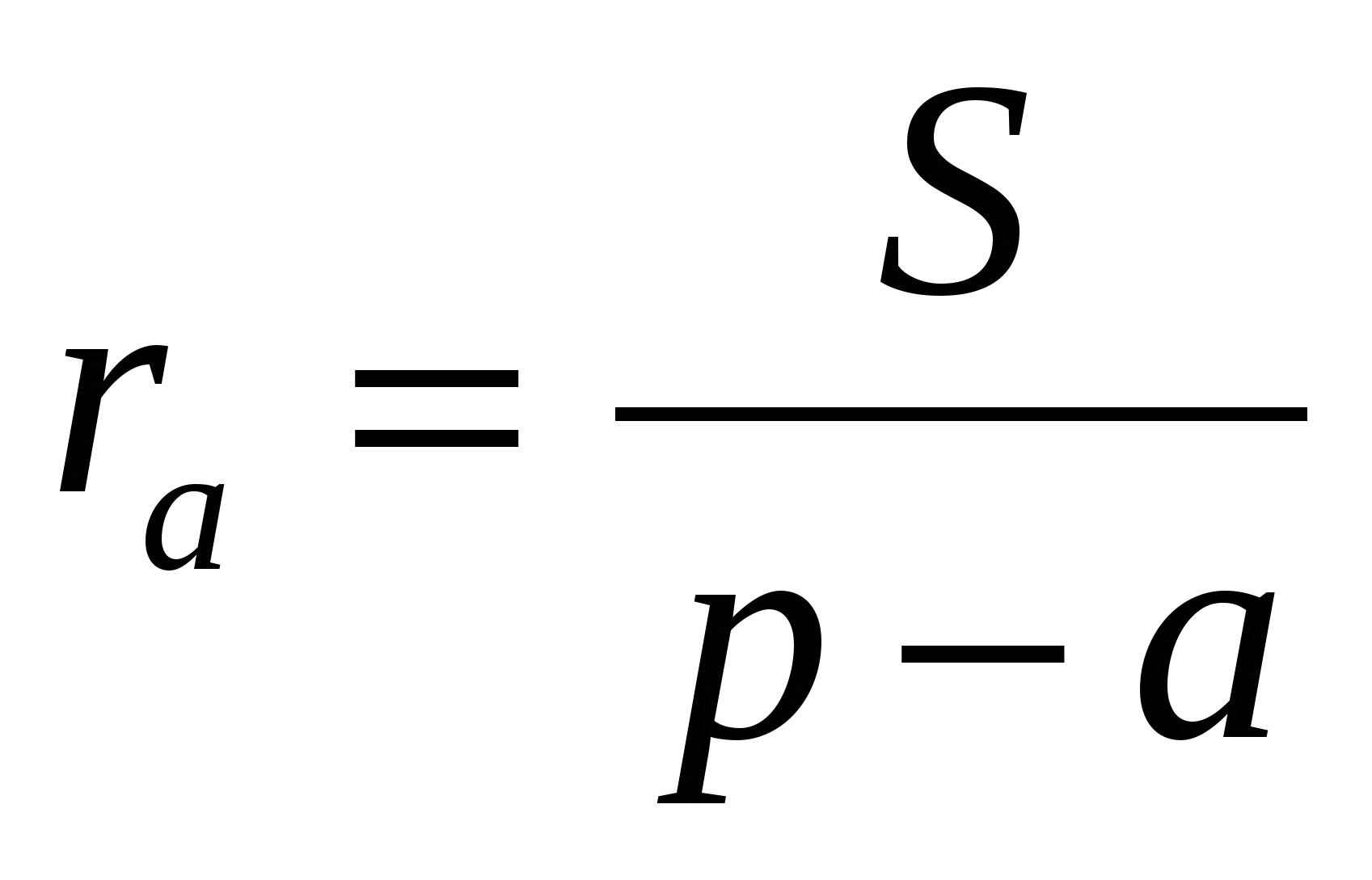
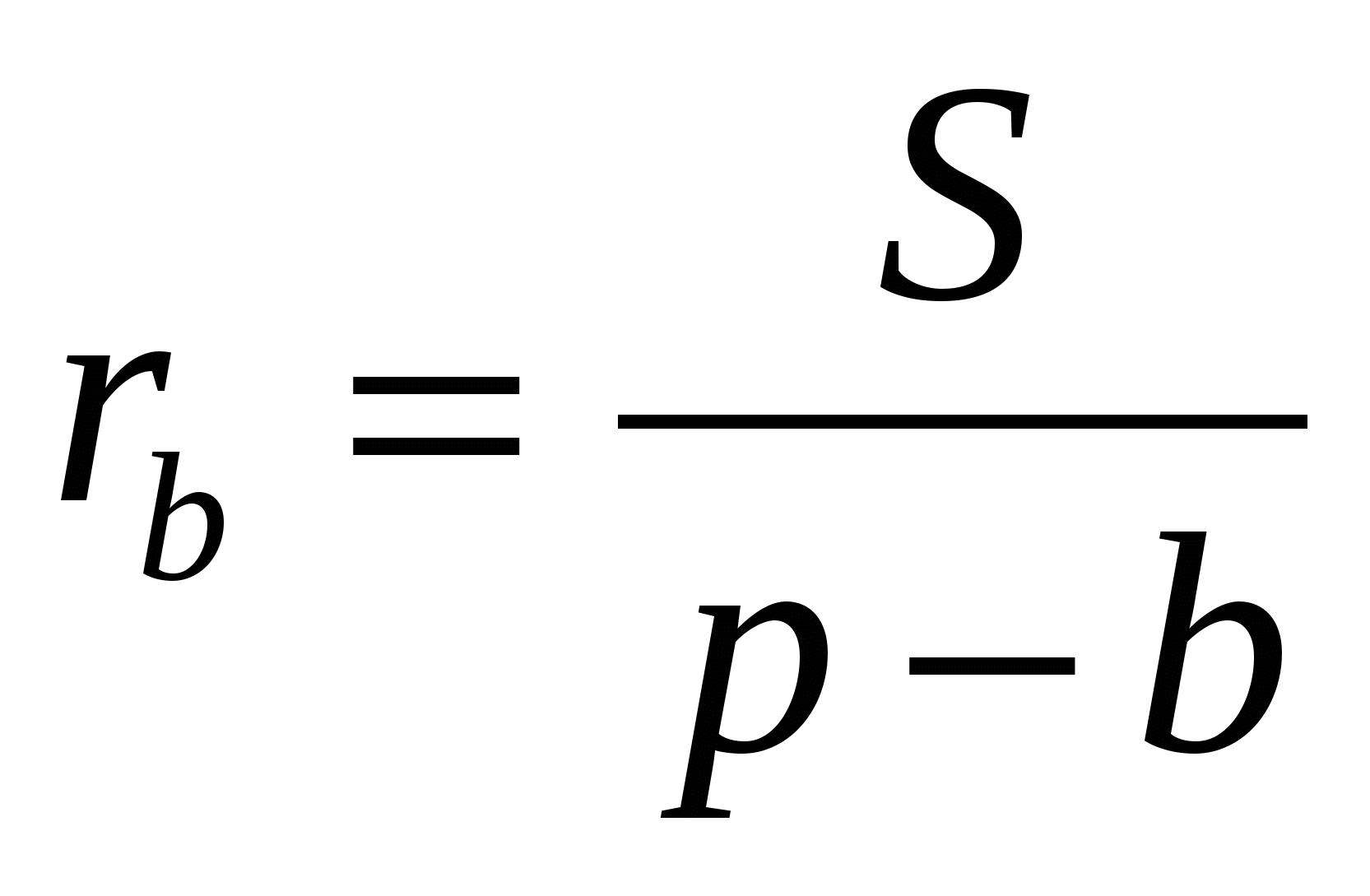
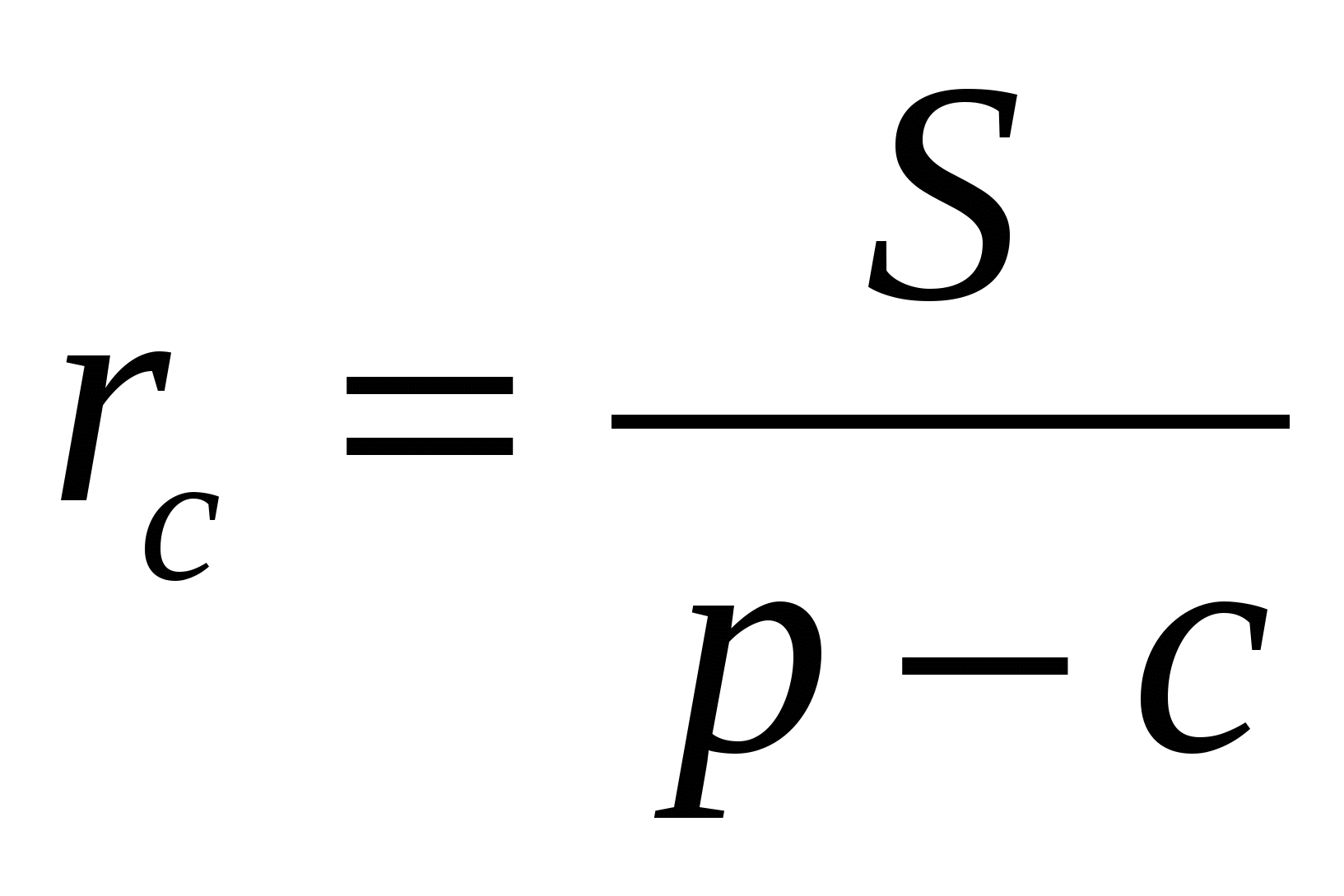
Утверждение. Пусть соответственно площадь, полупериметр и стороны некоторого треугольника, а — радиусы вневписанных окружностей, то , и .

Доказательство. Центром окружности, вписанной в угол А, служит точка О_а (точка пересечения биссектрис внешних углов треугольника, не смежных с углом А; радиус этой окружности есть отрезок перпендикуляра, проведенного из точки О_а к какой-либо стороне треугольника (или ее продолжению): .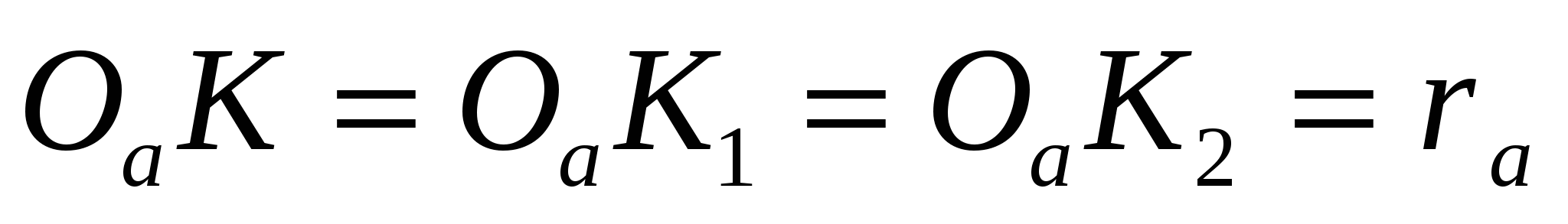

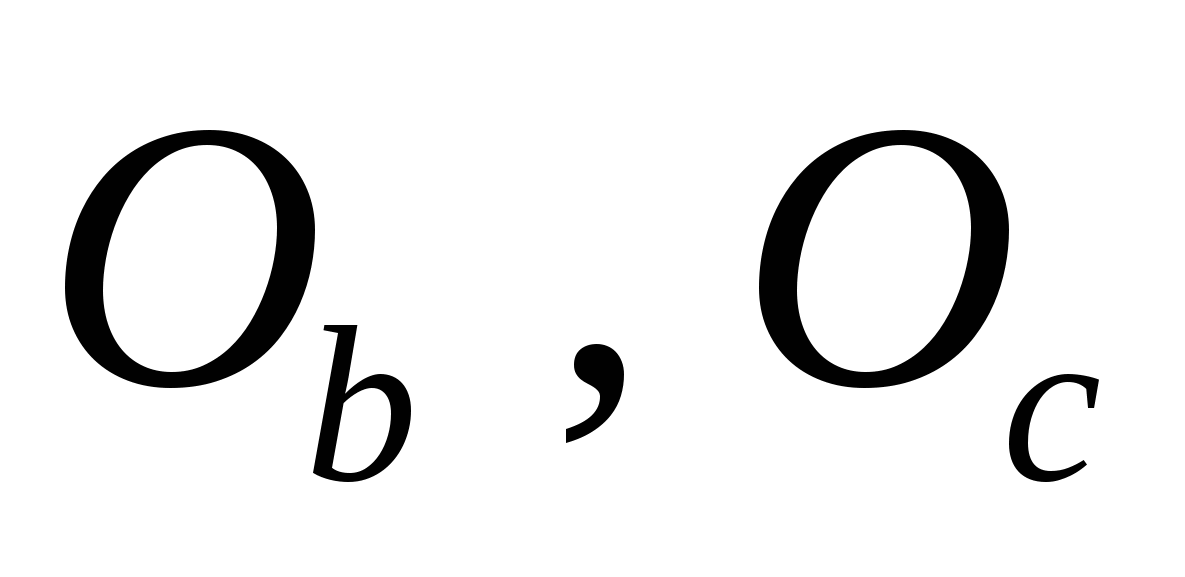
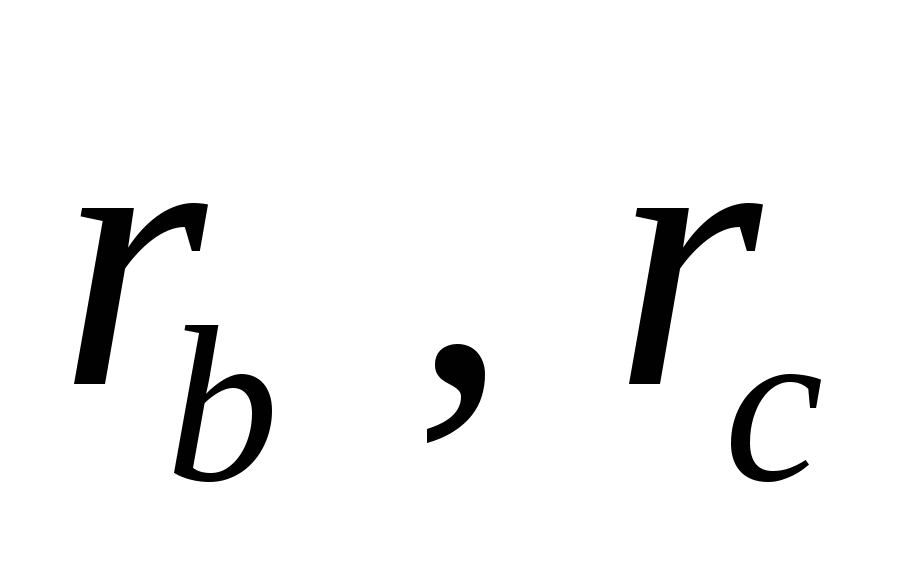
Аналогично можно найти центры и радиусы двух других вневписанных окружностей.

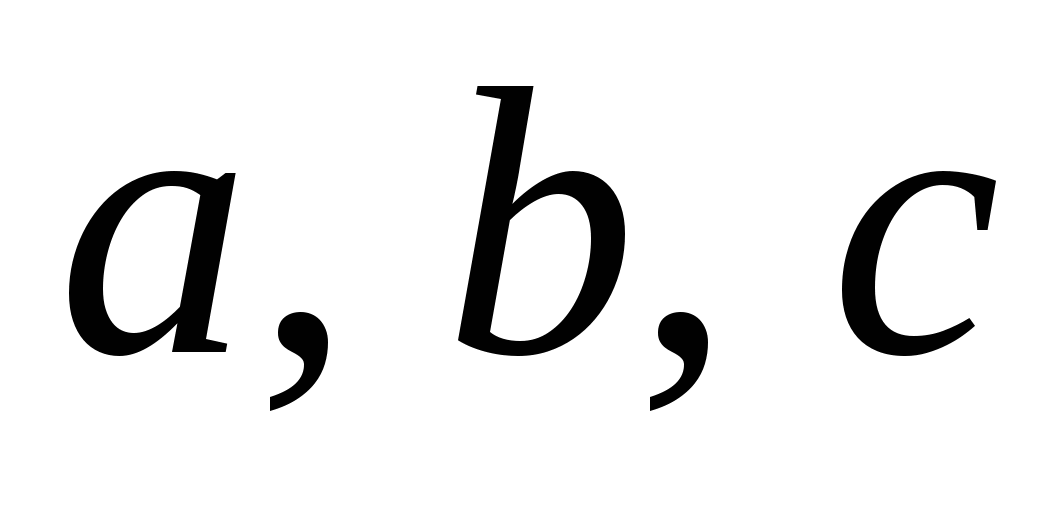
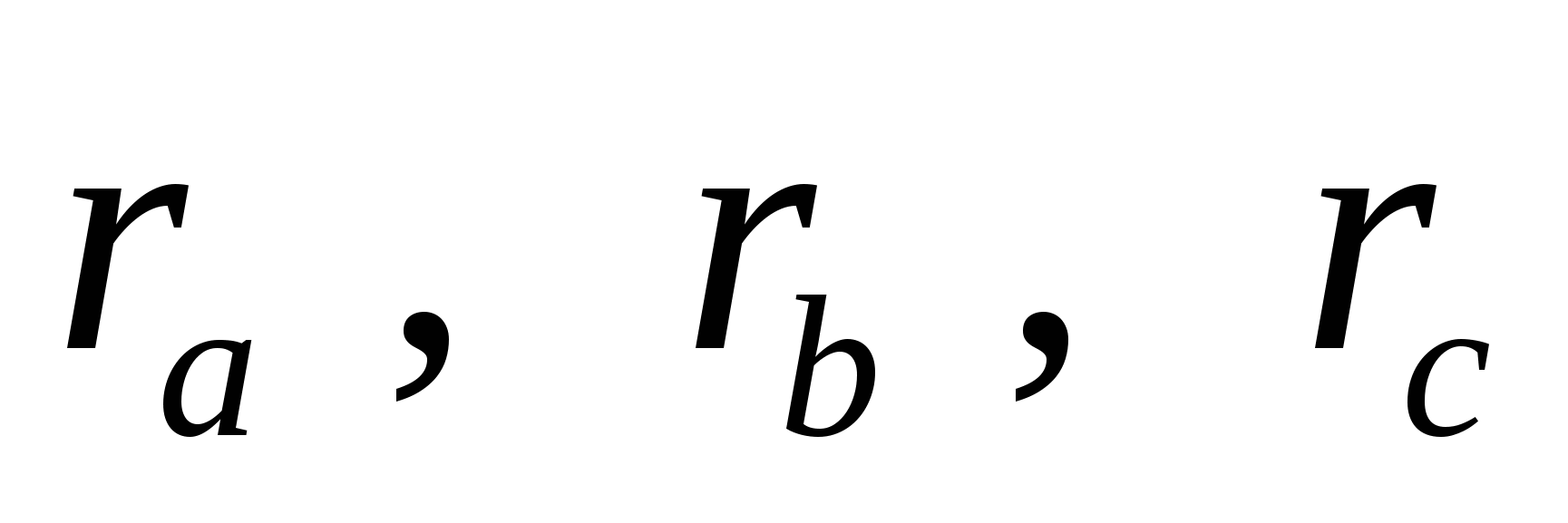
Зная длины сторон треугольника ABC , можно вычислить длины .

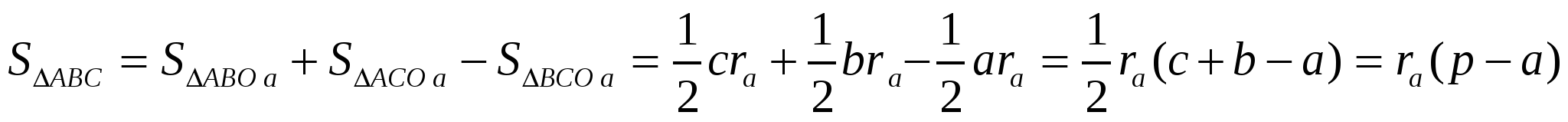
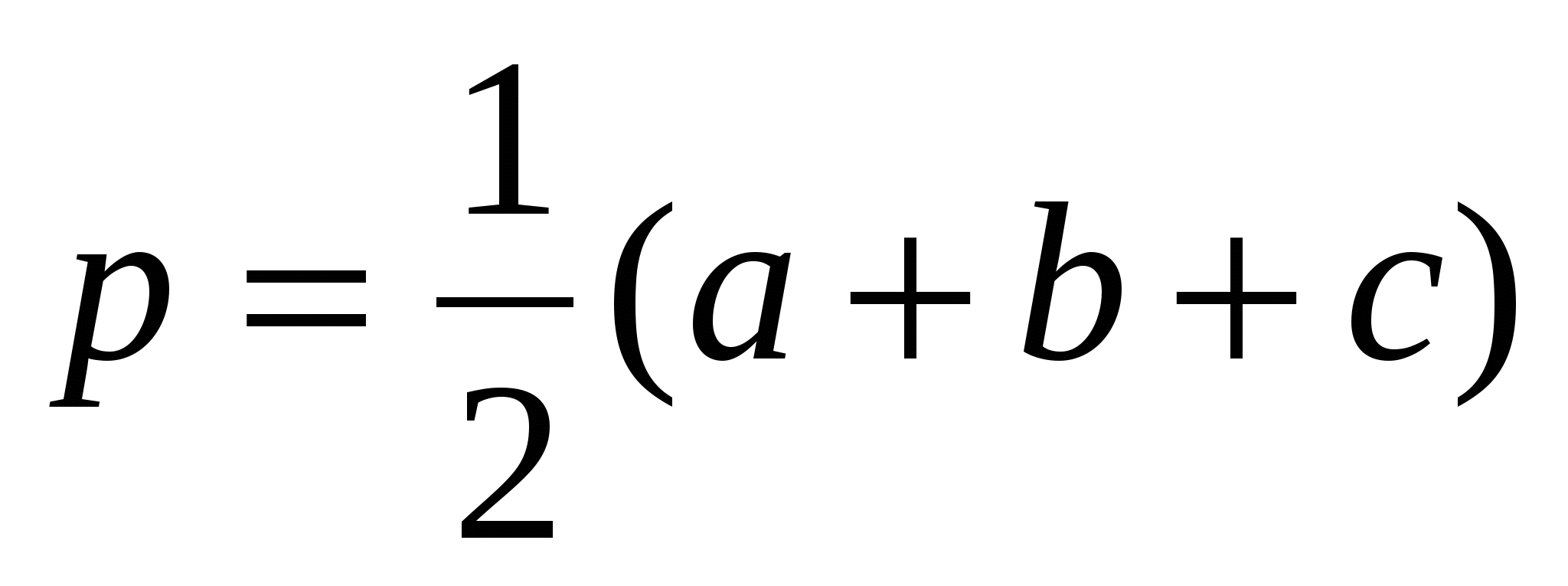
Действительно, , где .

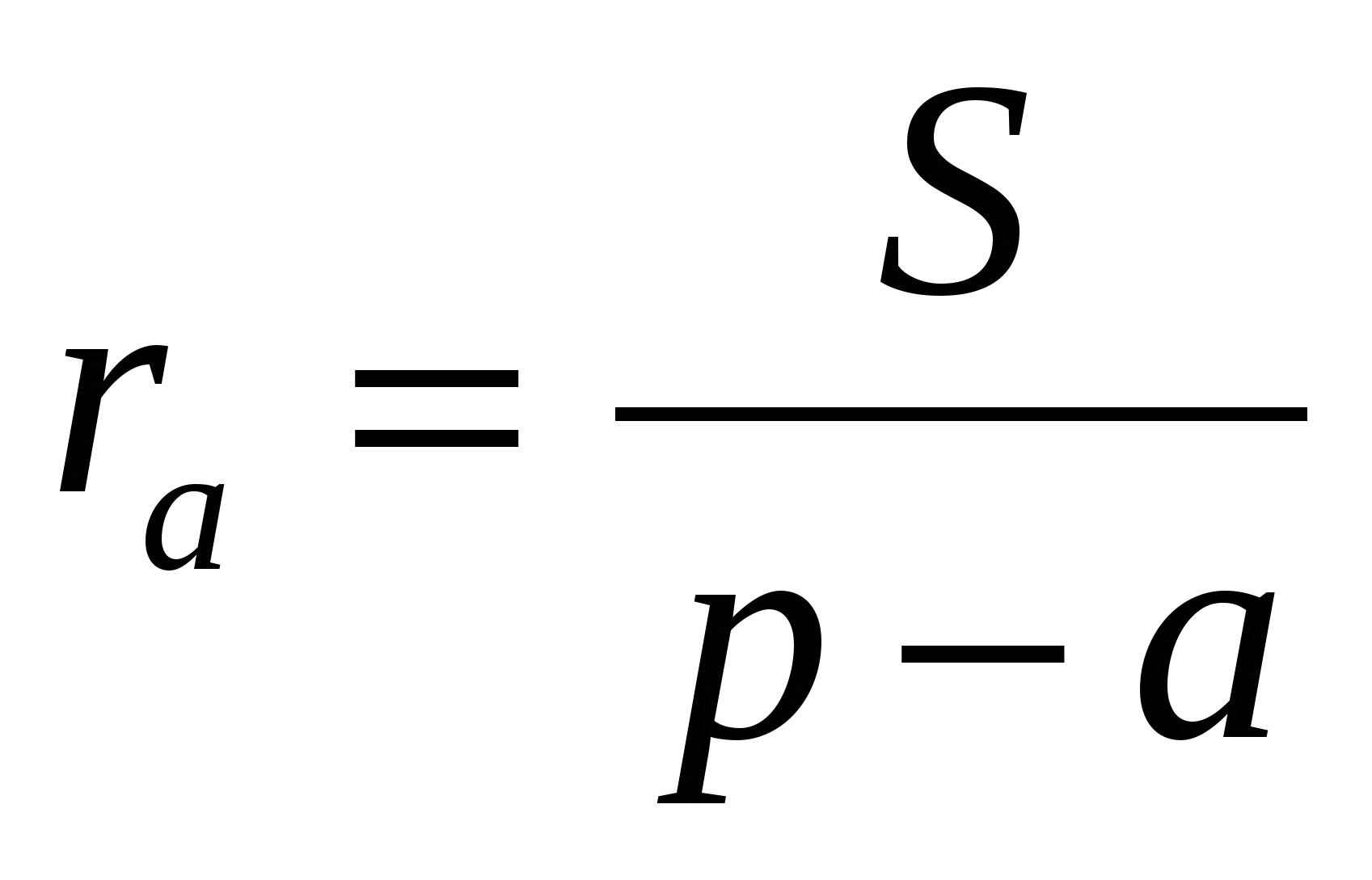
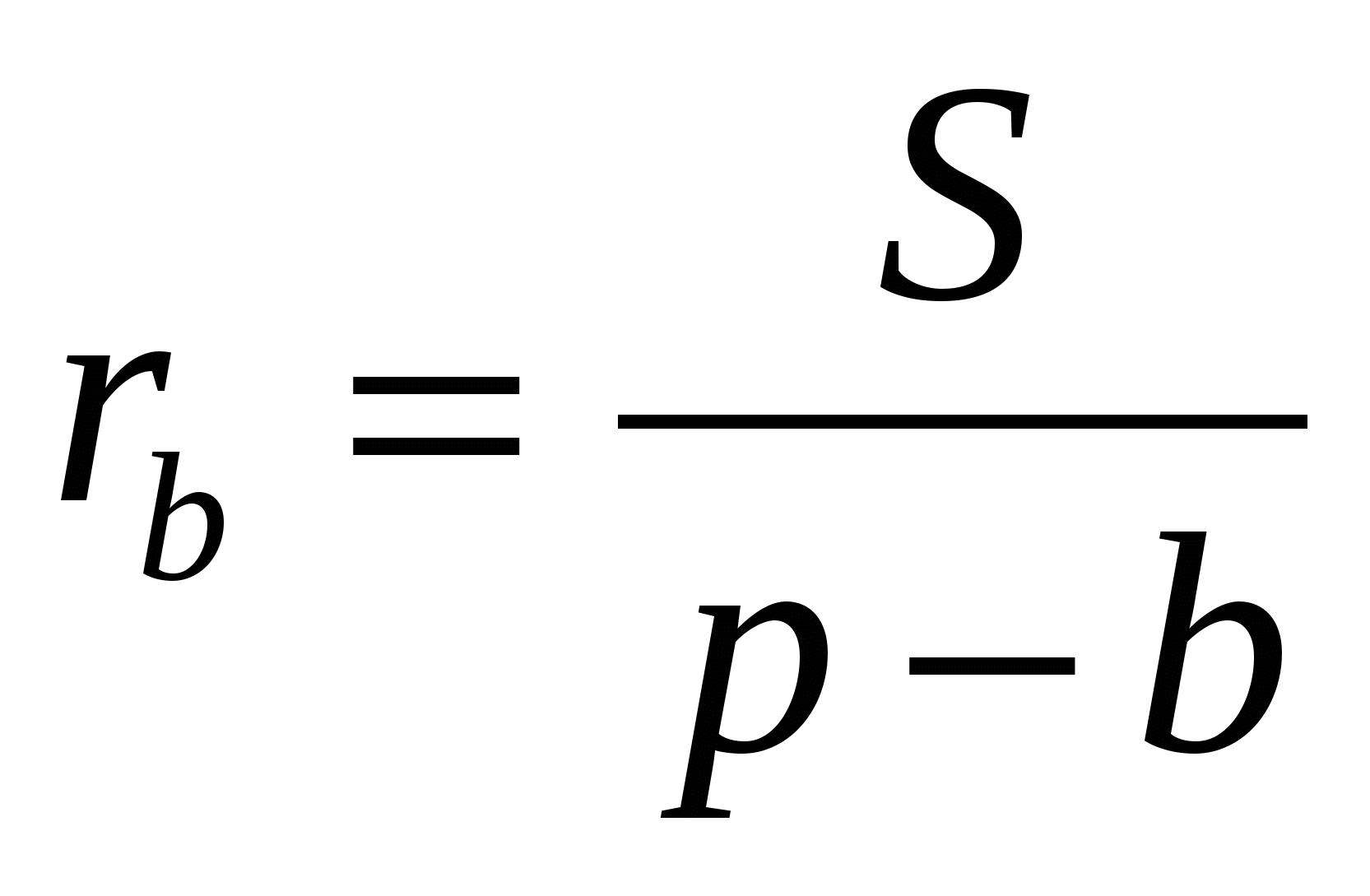
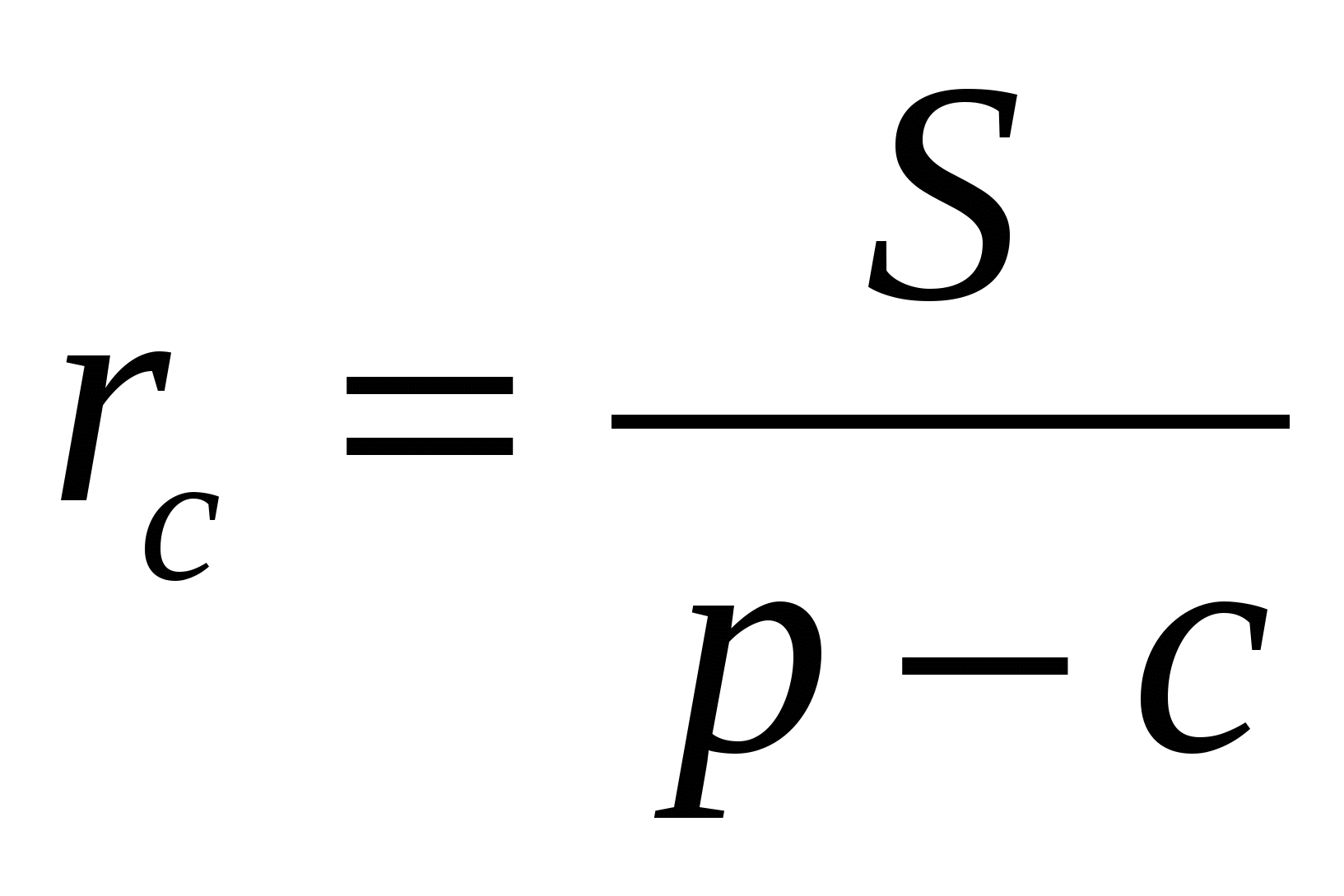
Отсюда . Аналогично: , .

Для радиуса вписанной окружности .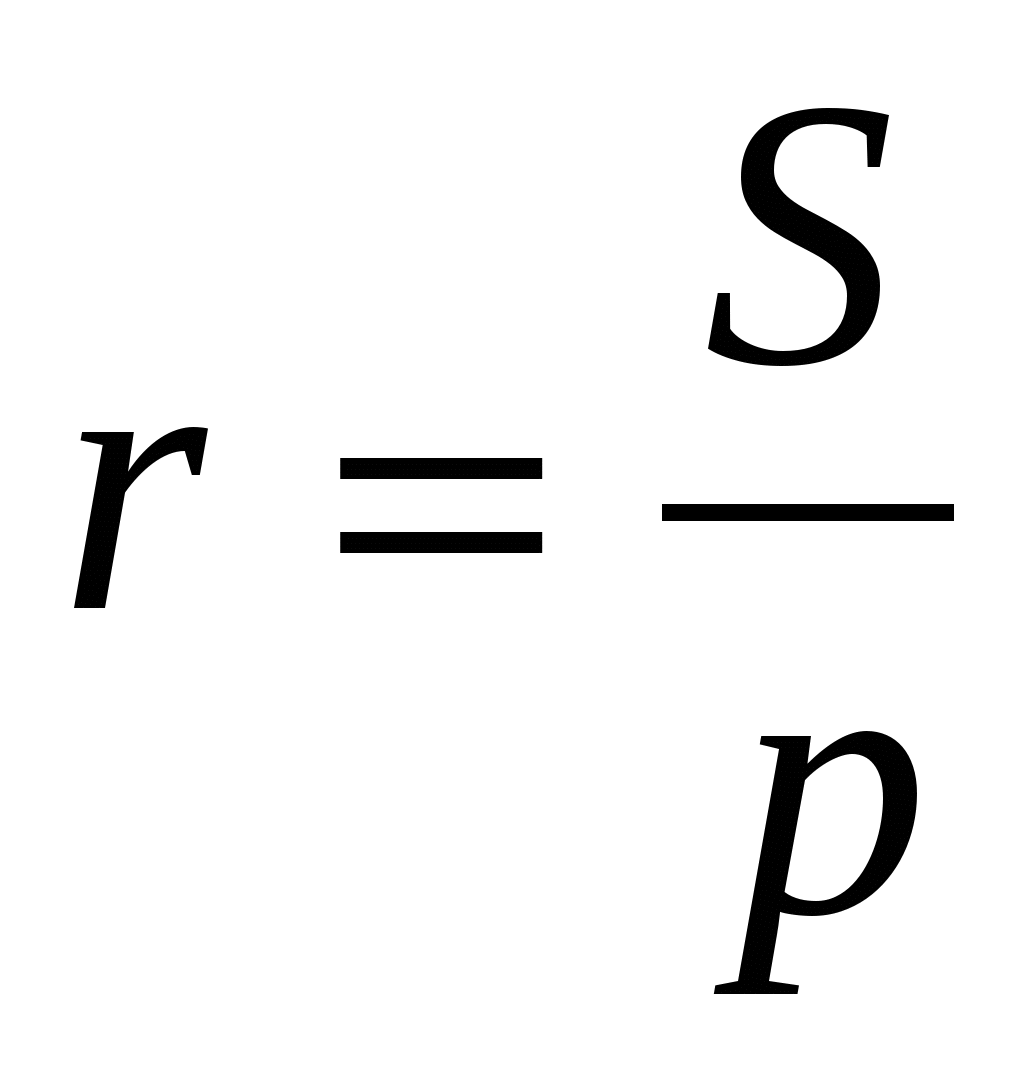

На основании доказанного можно сформулировать следующую теорему.

Теорема 3. Площадь S треугольника АВС равна

Радиусы описанной, вписанной и вневписанных окружностей также связаны красивыми соотношениями:

(1),

(2),

(3),

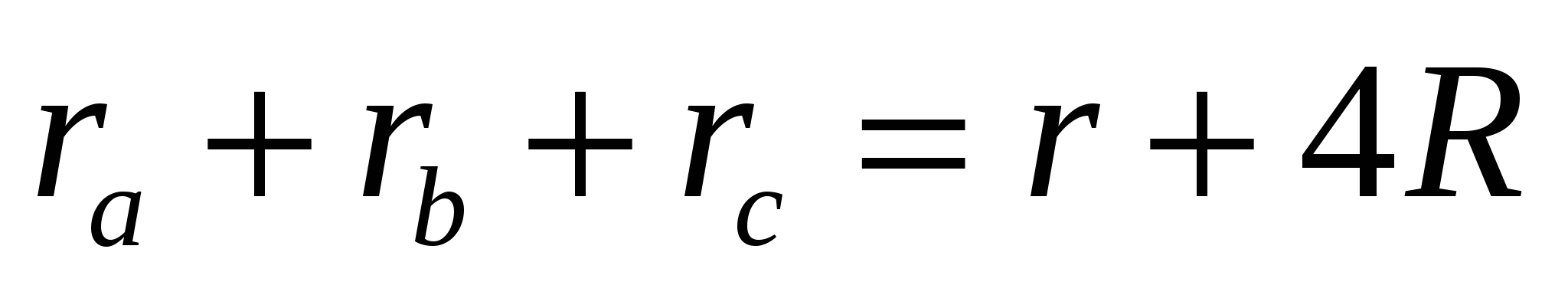
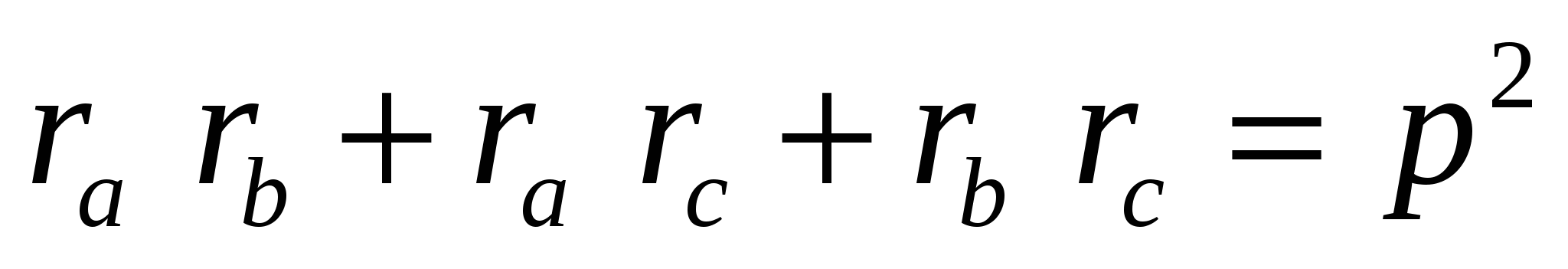
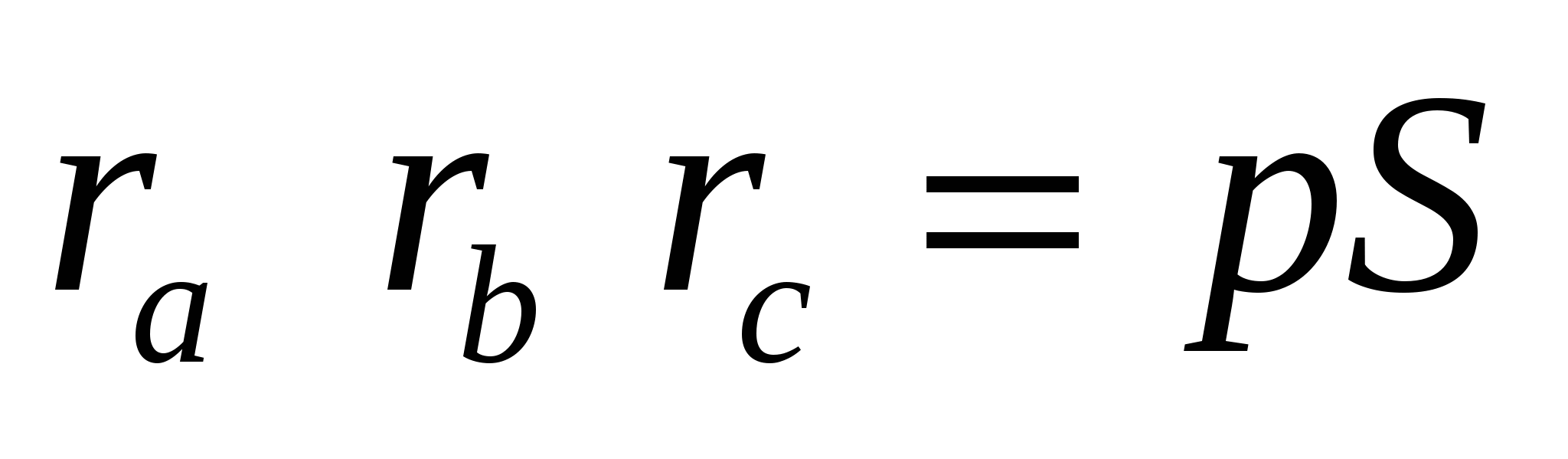
где 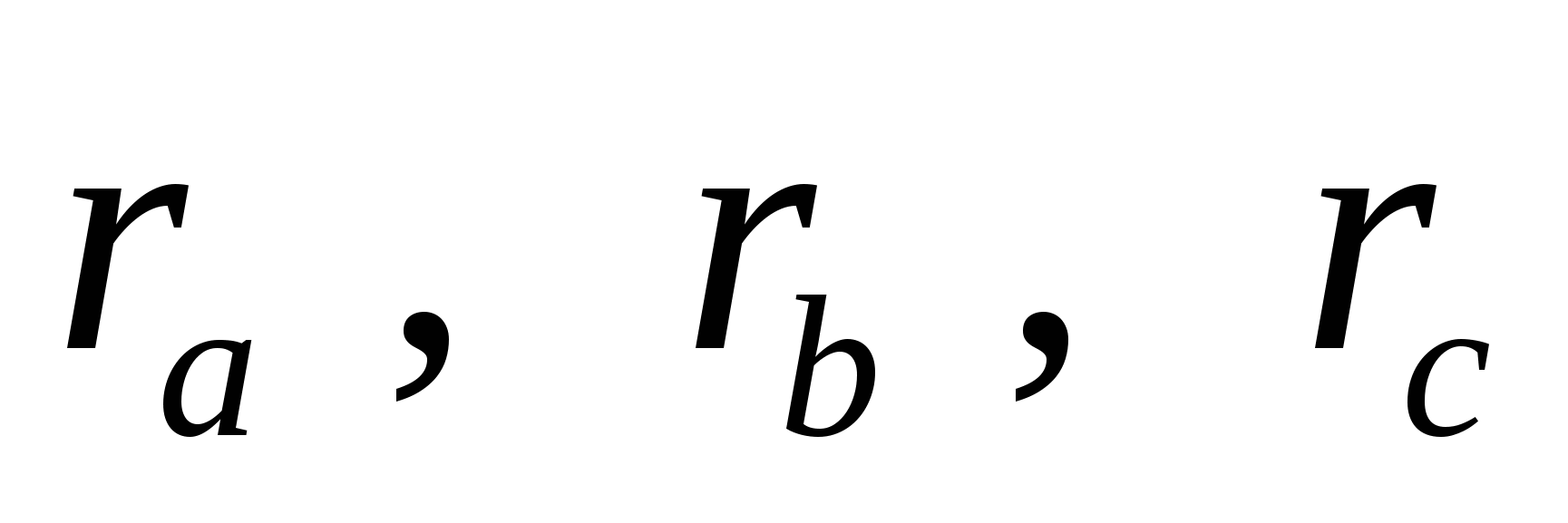— радиусы вневписанных окружностей, R и r – соответственно радиусы описанной и вписанной окружностей, р – полупериметр, S- площадь треугольника.

Докажем равенство (1):

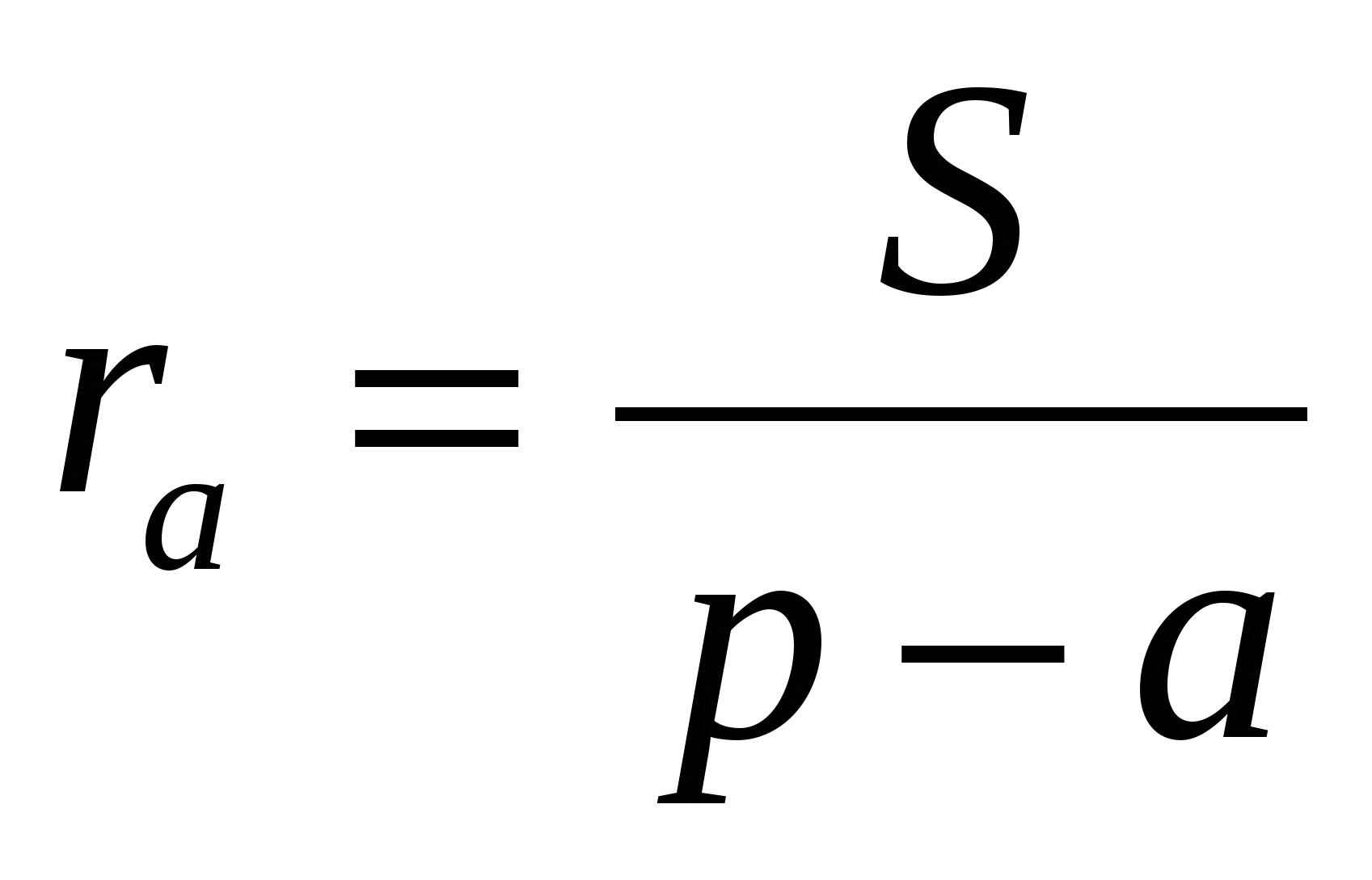
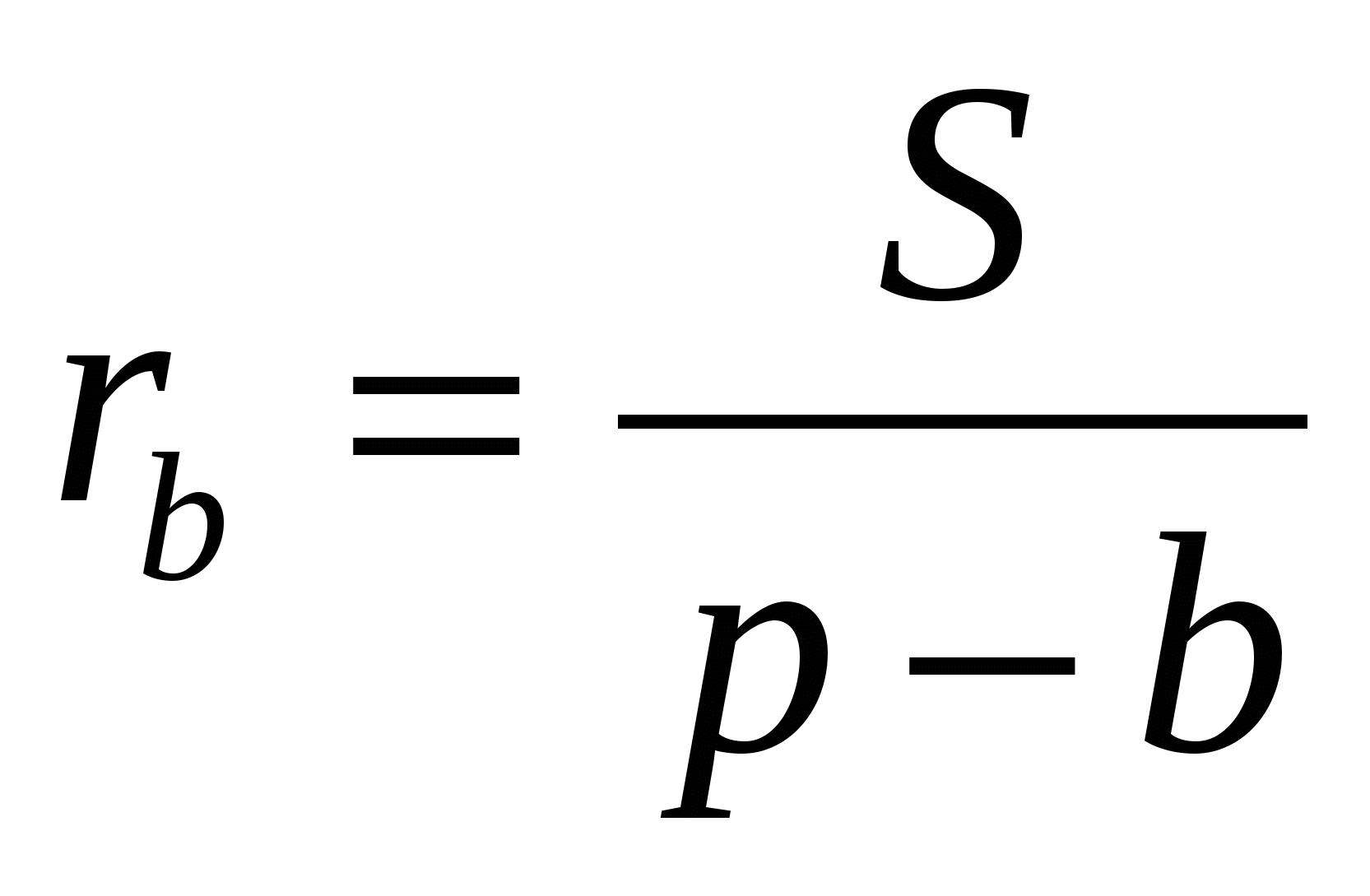
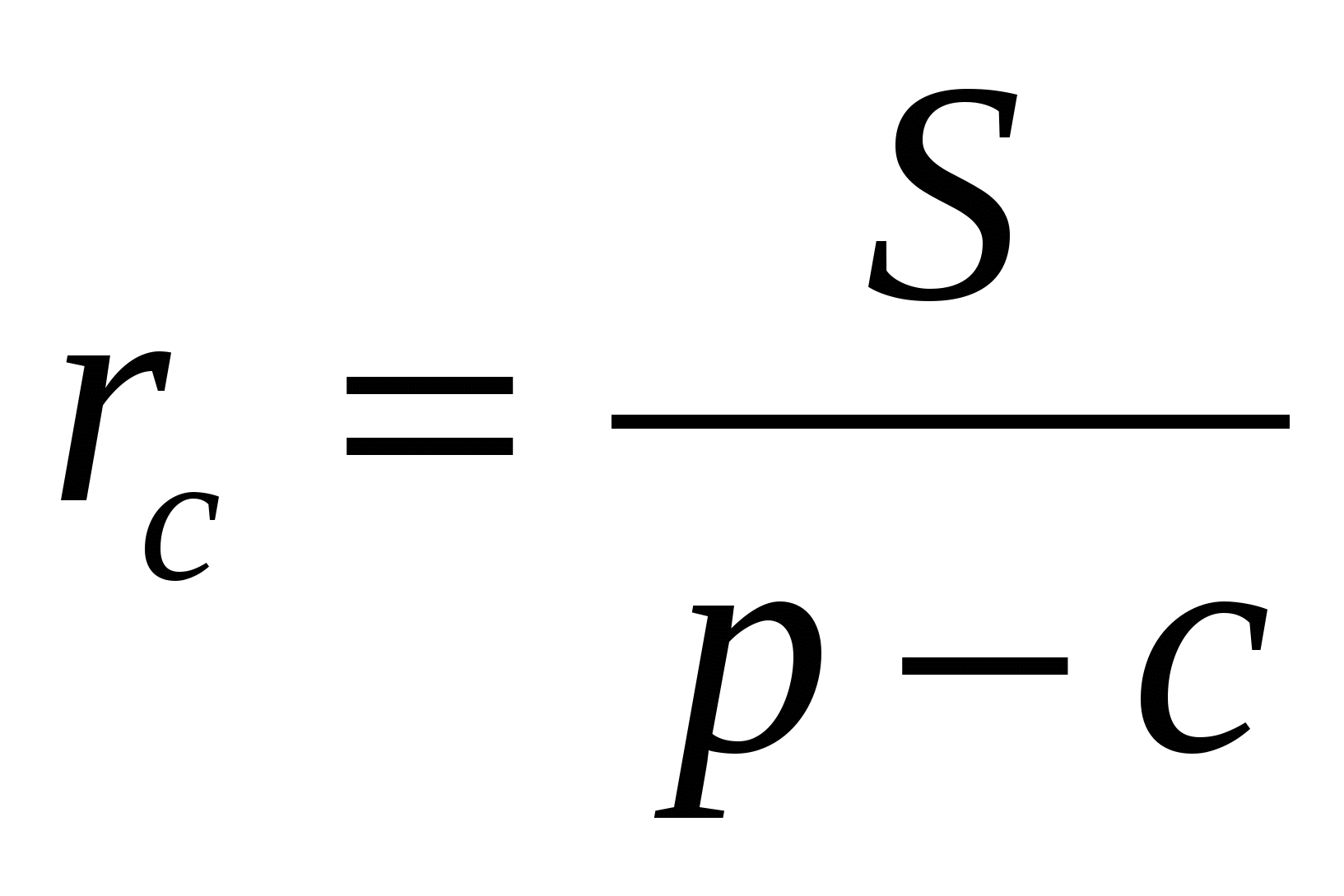
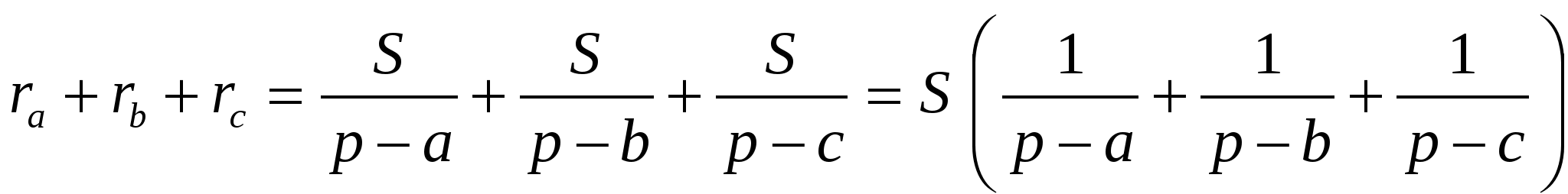
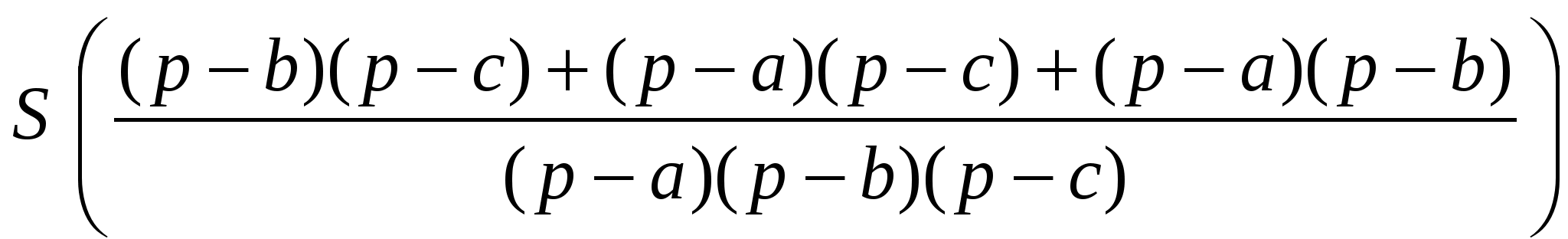
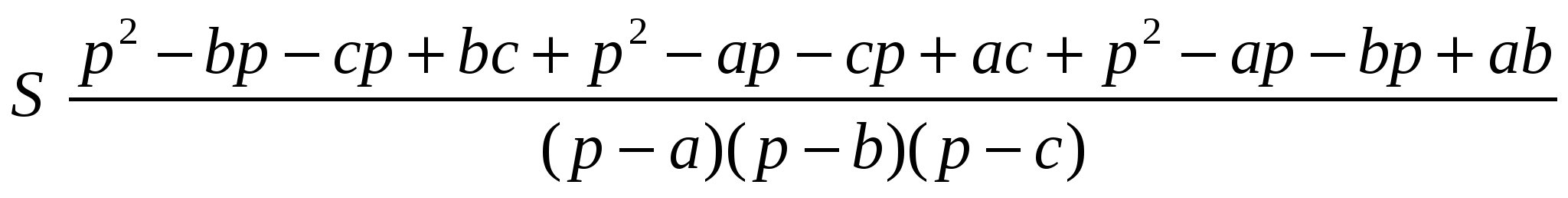
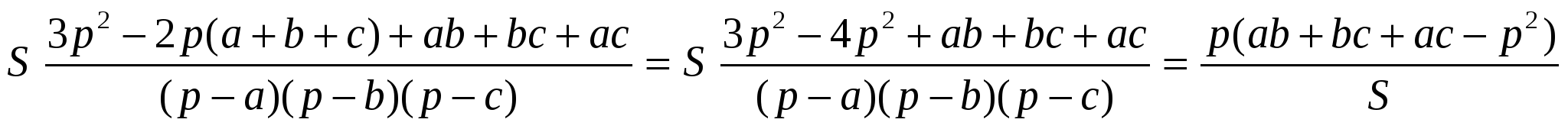
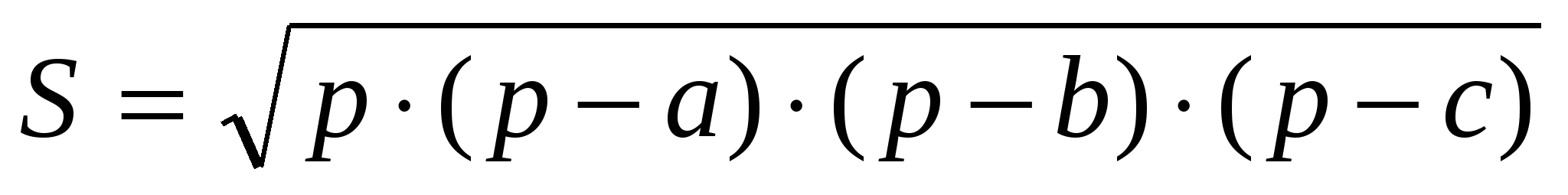
Учитывая, что , , , имеем: = ==

==

= , так как по формуле Герона .

С другой стороны: =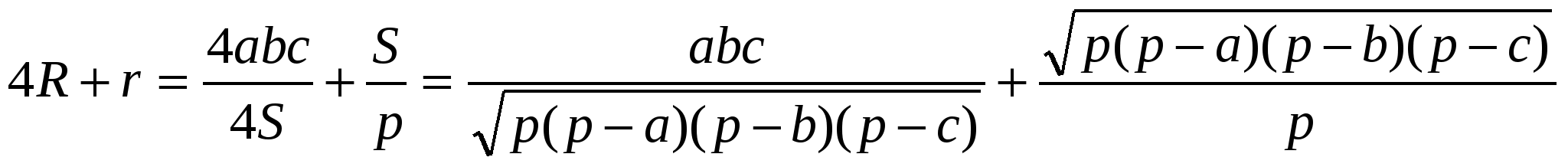

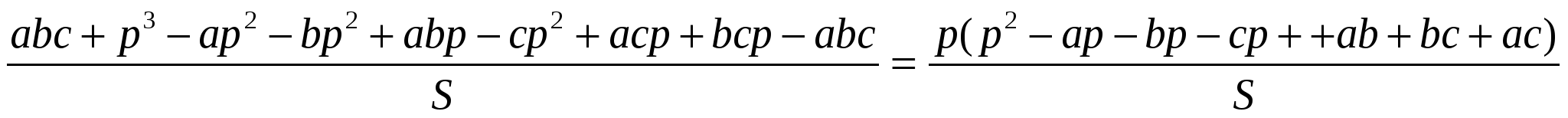
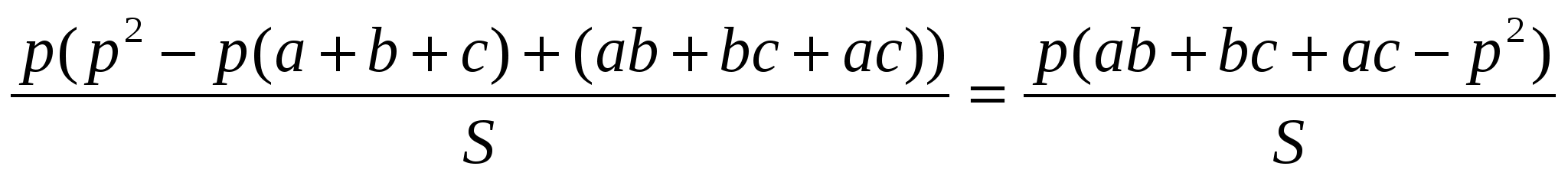
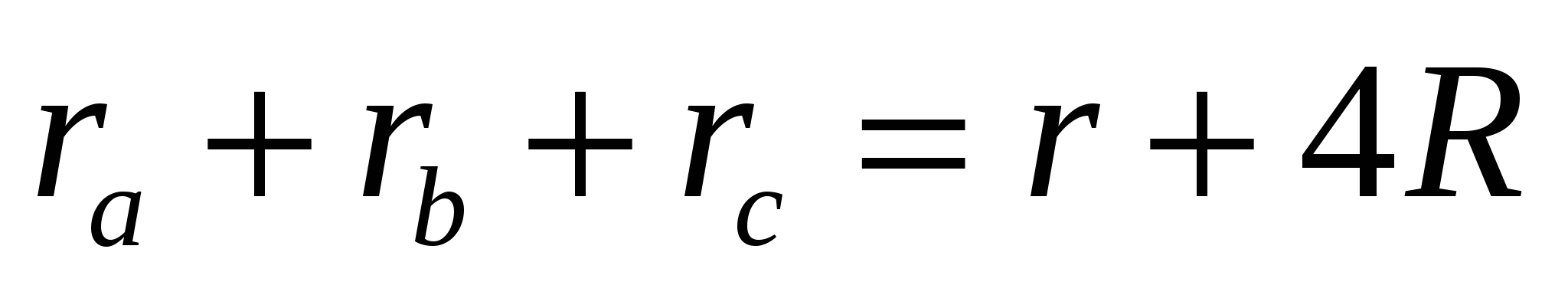
=. Таким образом .

Докажем равенство (2): =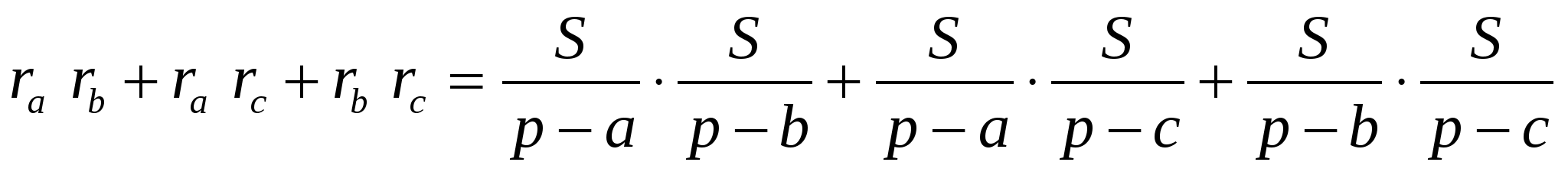

=

= .

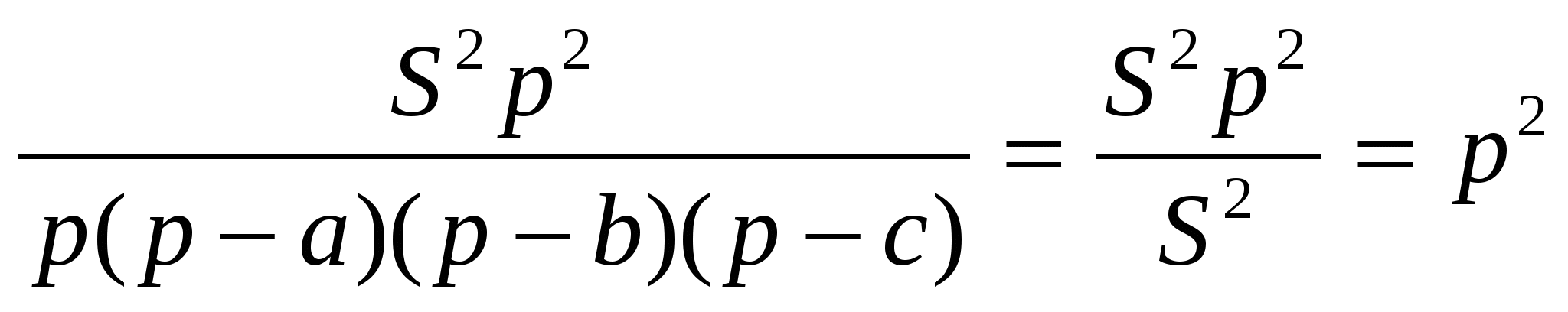
Докажем равенство (3): .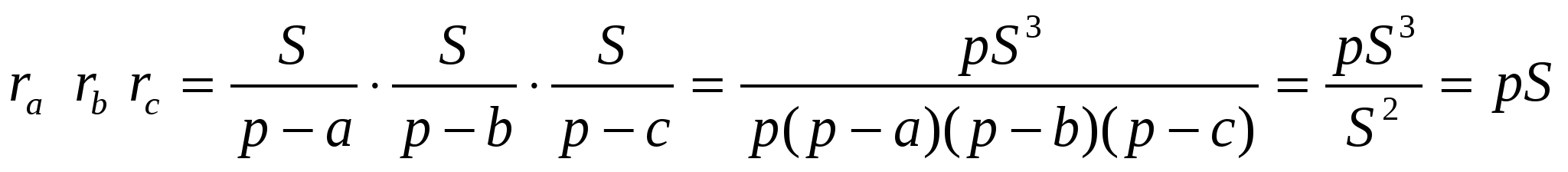

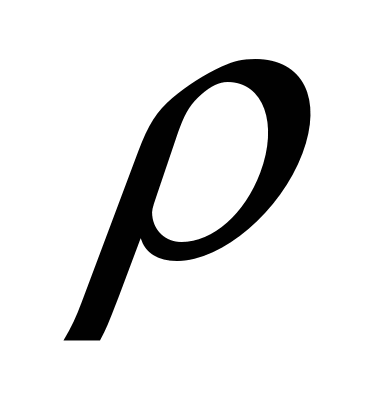
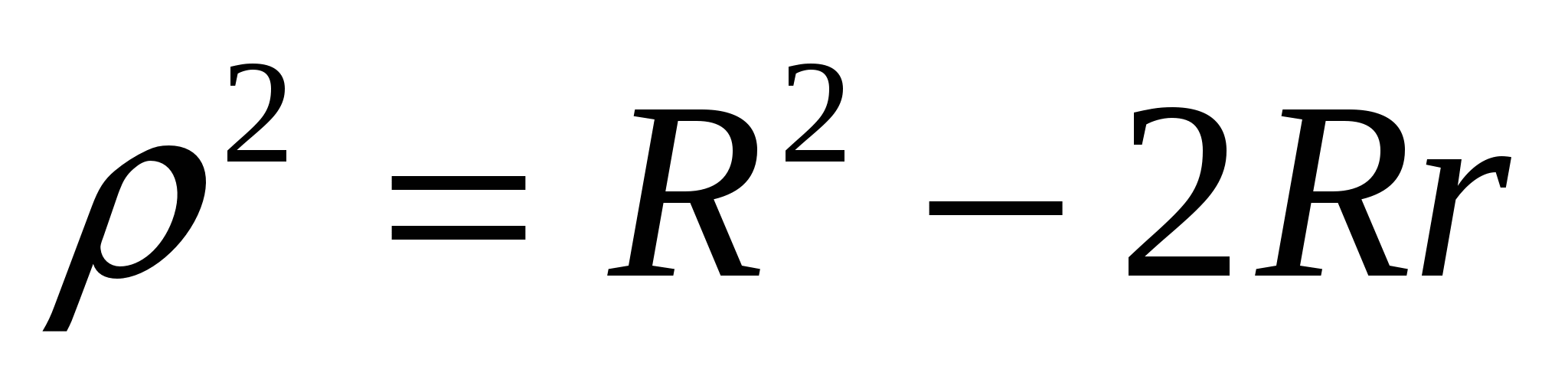
Известно, что расстояние между центрами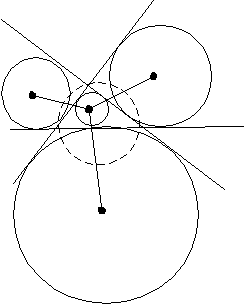 вписанной и описанной окружностей можно найти по формуле Эйлера: .

Интересно, что отрезки, соединяющие центр вписанной в треугольник окружности с центрами вневписанных окружностей, делятся пополам окружностью, описанной вокруг этого треугольник (рис.9).

Существует также теорема, связывающая между собой радиусы вписанной и вневписанных окружностей.

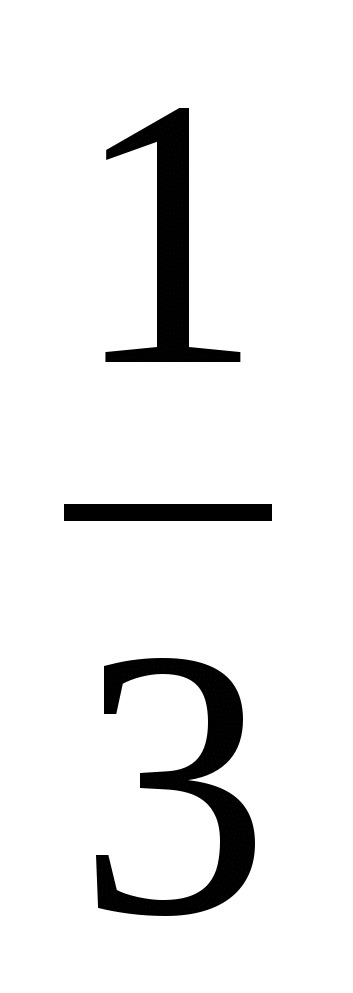
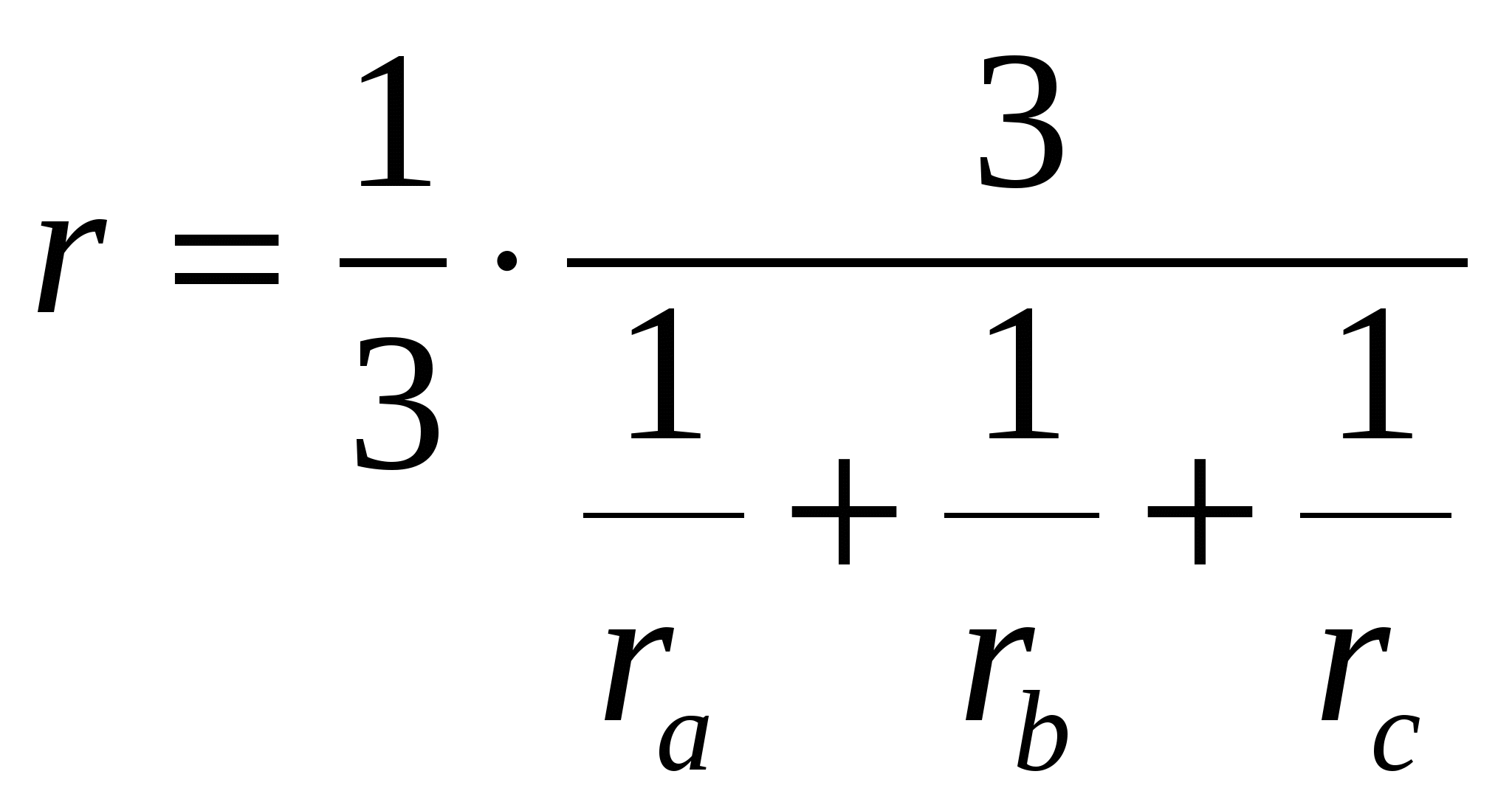
Теорема 4. Радиус вписанной окружности треугольника равен среднего гармонического радиусов вневписанных окружностей этого треугольника, т.е. .

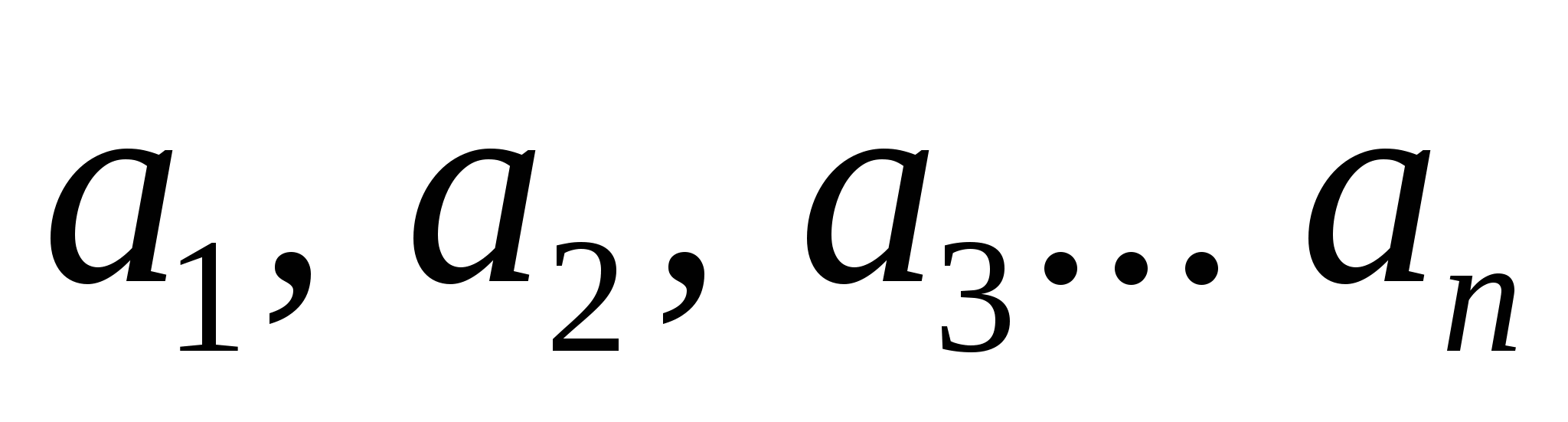
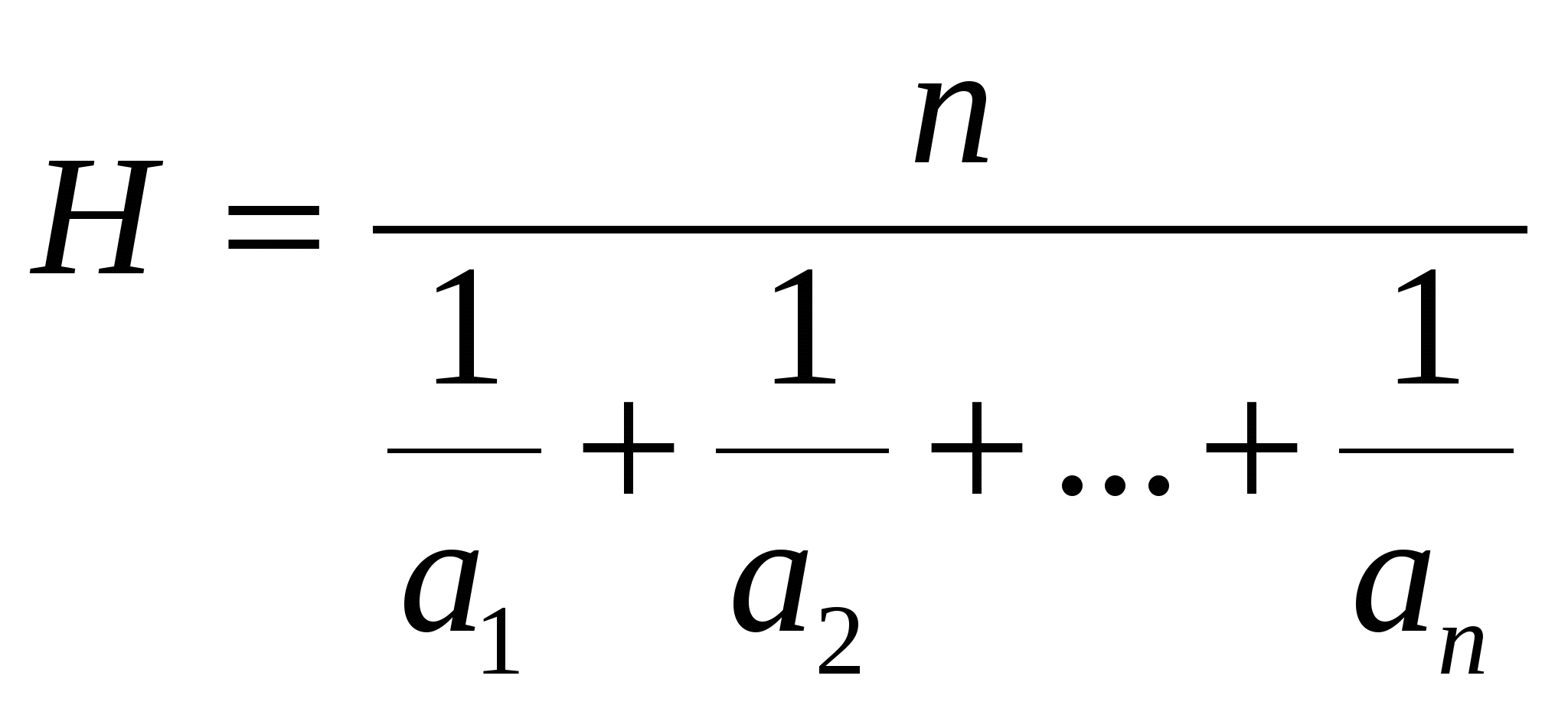
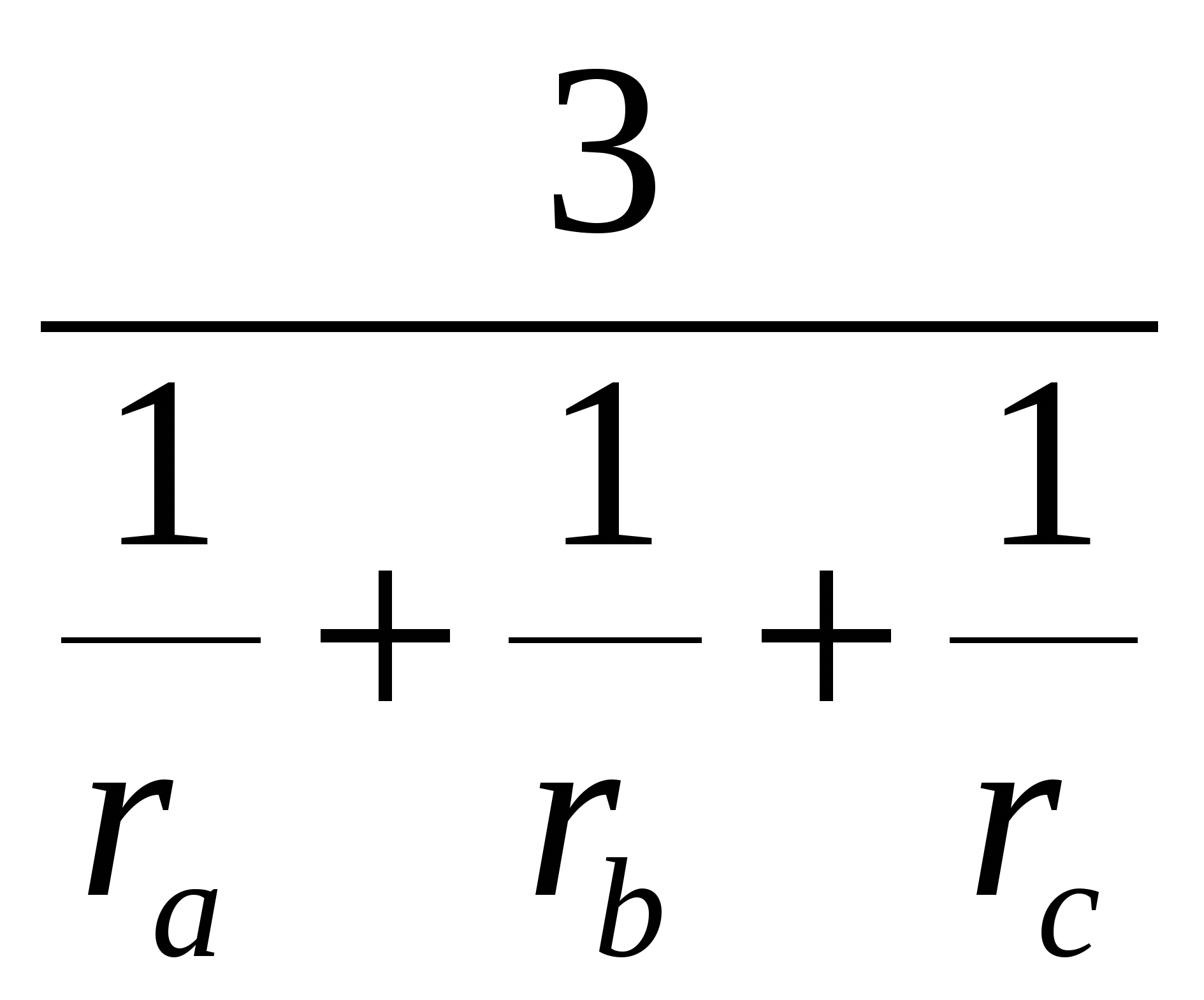
Доказательство. Как известно, среднее гармоническое неотрицательных чисел вычисляется по формуле , значит, среднее гармоническое радиусов вневписанных окружностей треугольника будет равна .

Преобразуем выражение .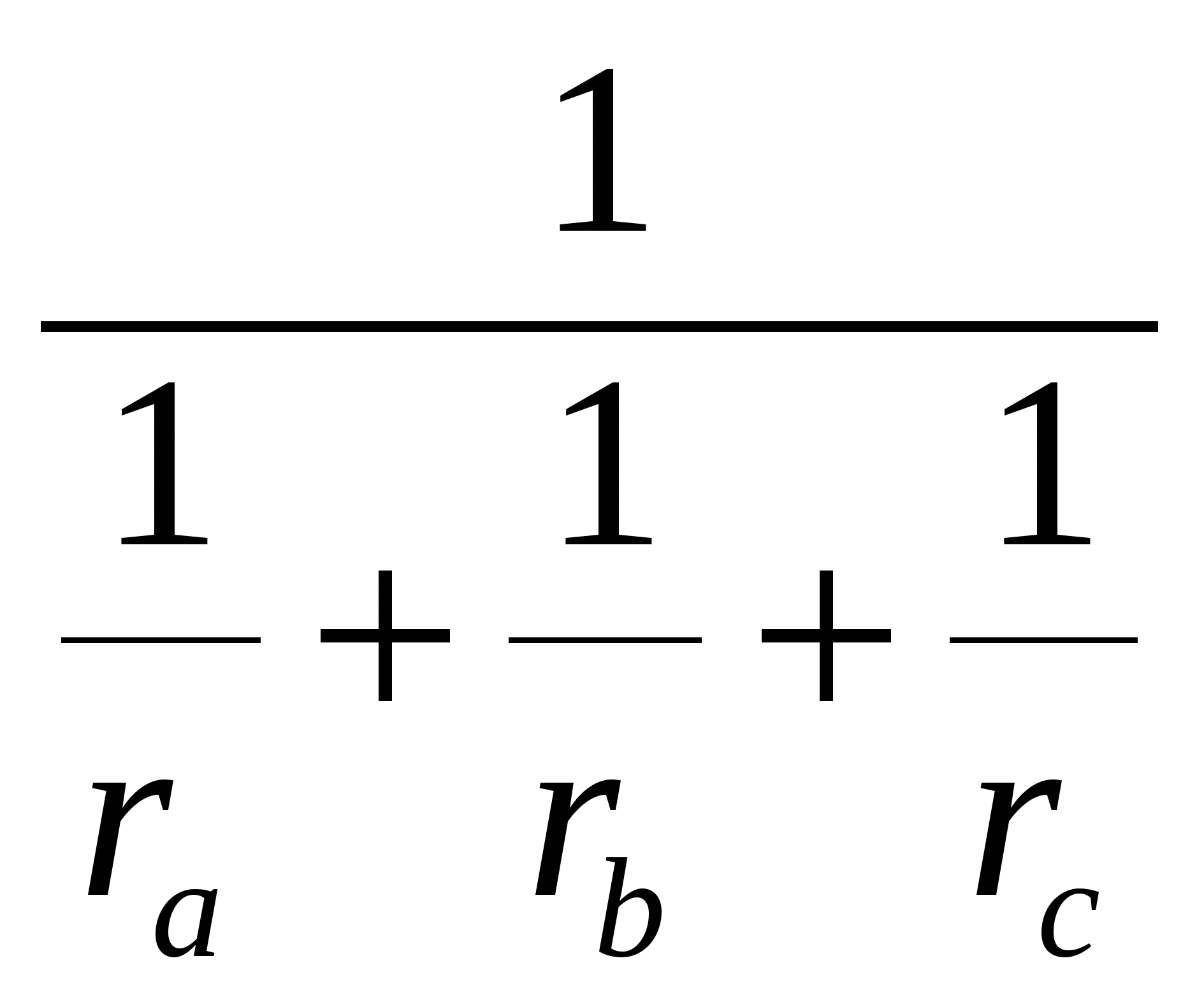

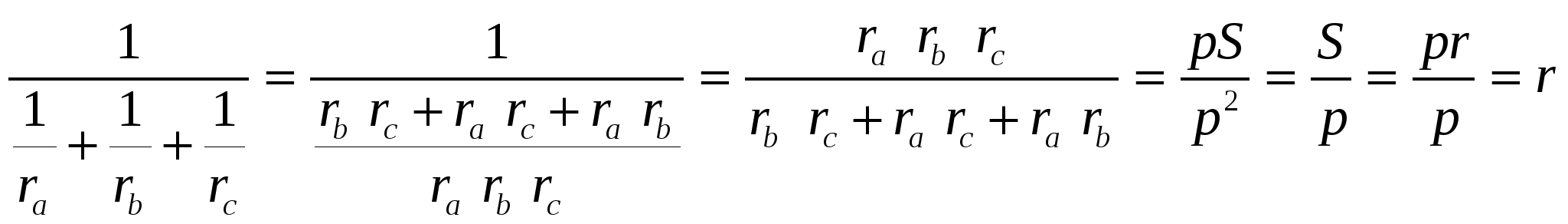
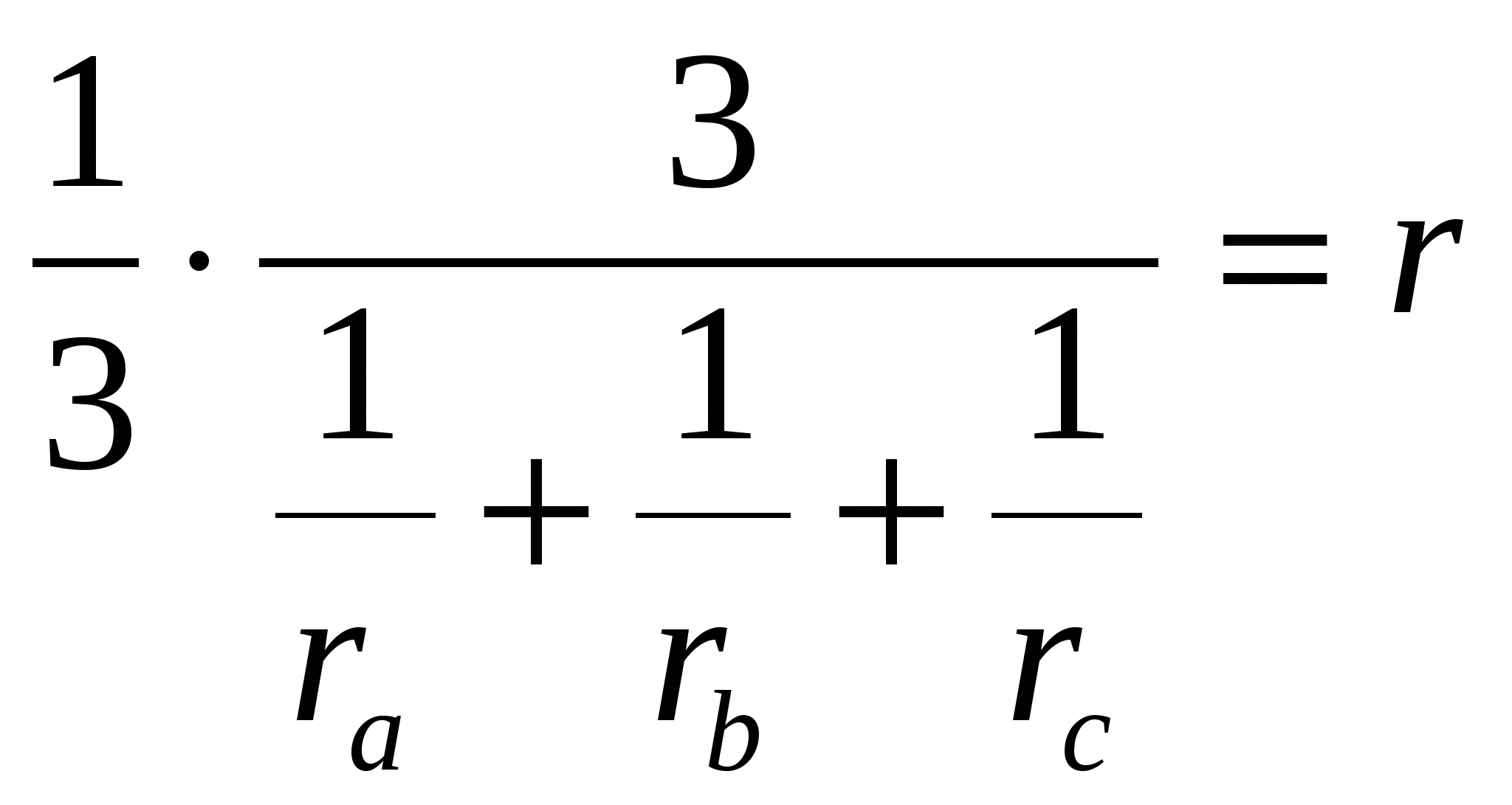
. Следовательно, .

Очевидно следующее следствие этой теоремы: обратное значение радиуса вписанной окружности равно сумме обратных значений радиусов вневписанных окружностей треугольника.

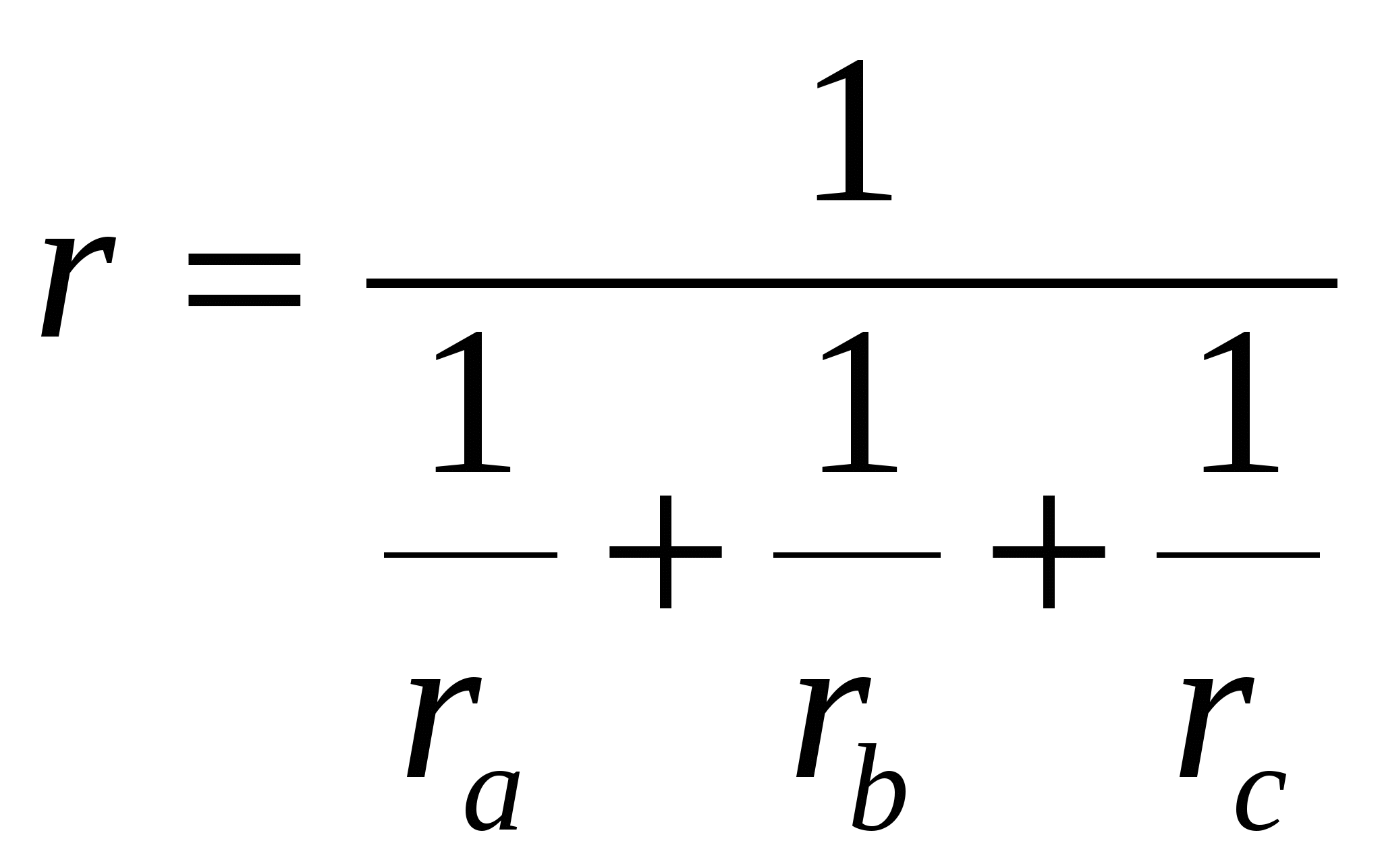
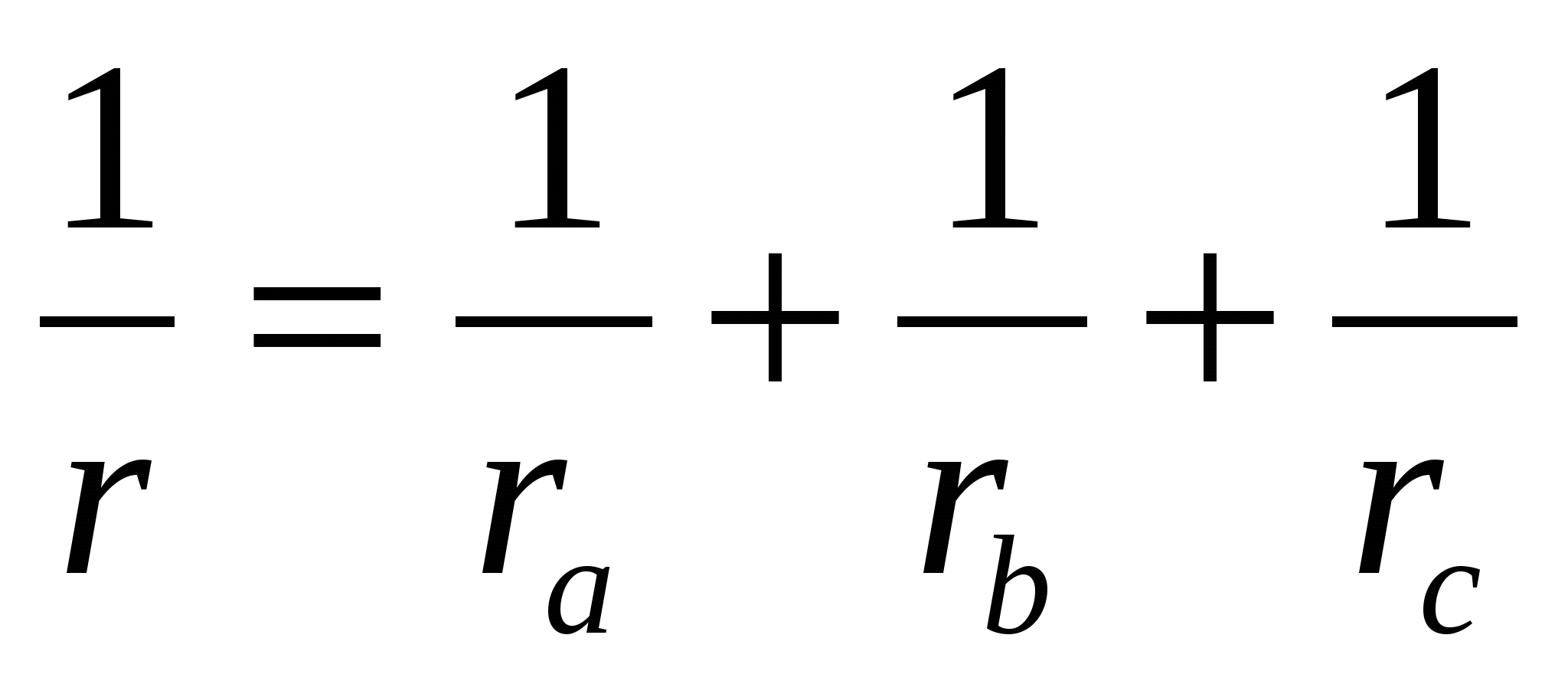
Если , то .

С использованием понятия «вневписанная окружность треугольника» можно доказать формулу Герона 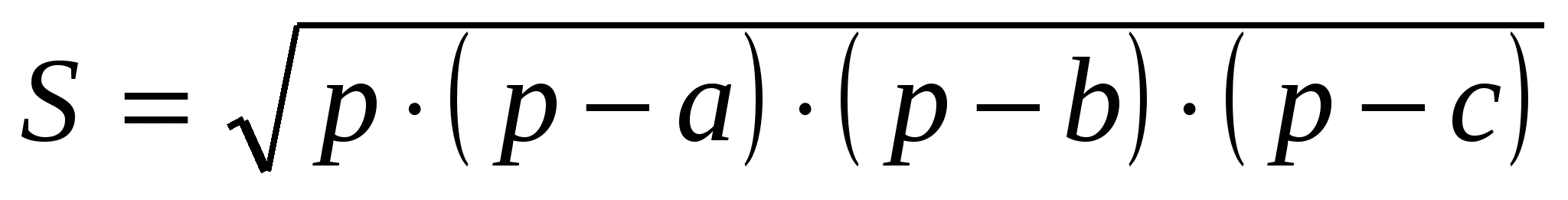. Прежде чем перейти к доказательству, решим две задачи.

Задача 1. Пусть а, в, с – длины сторон треугольника АВС. Найти длины отрезков, на которые делятся его стороны точками касания вписанной в него окружности.

Р

ешение. Если M , P и N – точки касания, то, обозначив AM через х и воспользовавшись Рис.10. свойством отрезков касательных,

проведенных к окружности из одной точки, получим: AP = x,

ВР = BN = с – x, CM = CN = b — x. Но BN + NC = a. Отсюда с – х + b – x = a, поэтому 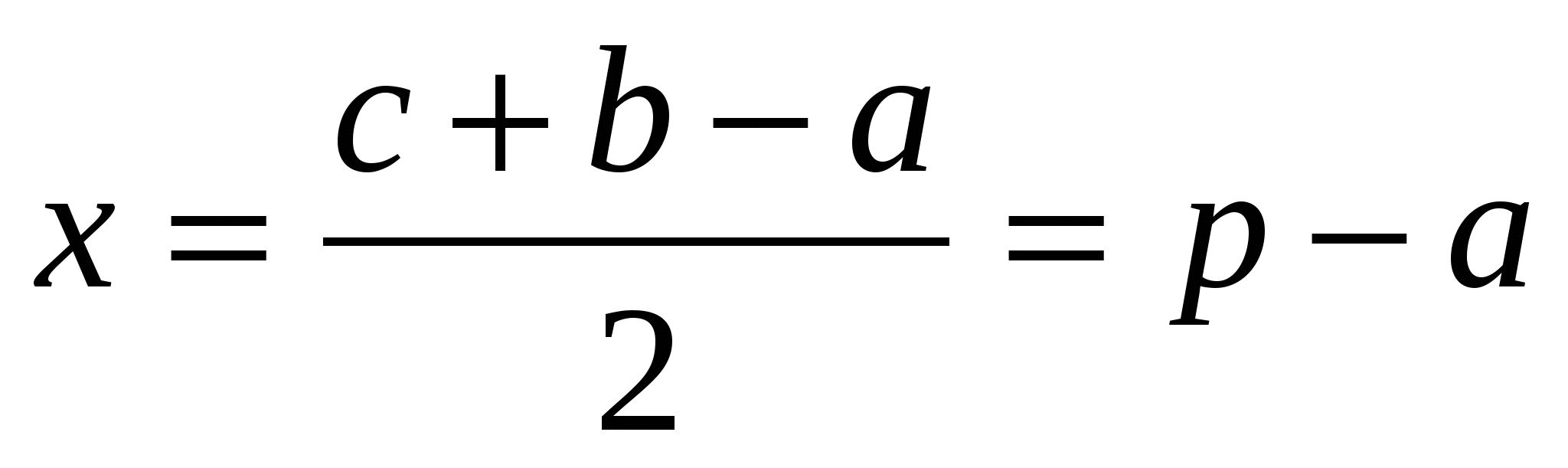. Таким образом, AP = AM = p – a. Так же можно вычислить и A x M b – x C

длины других отрезков: , .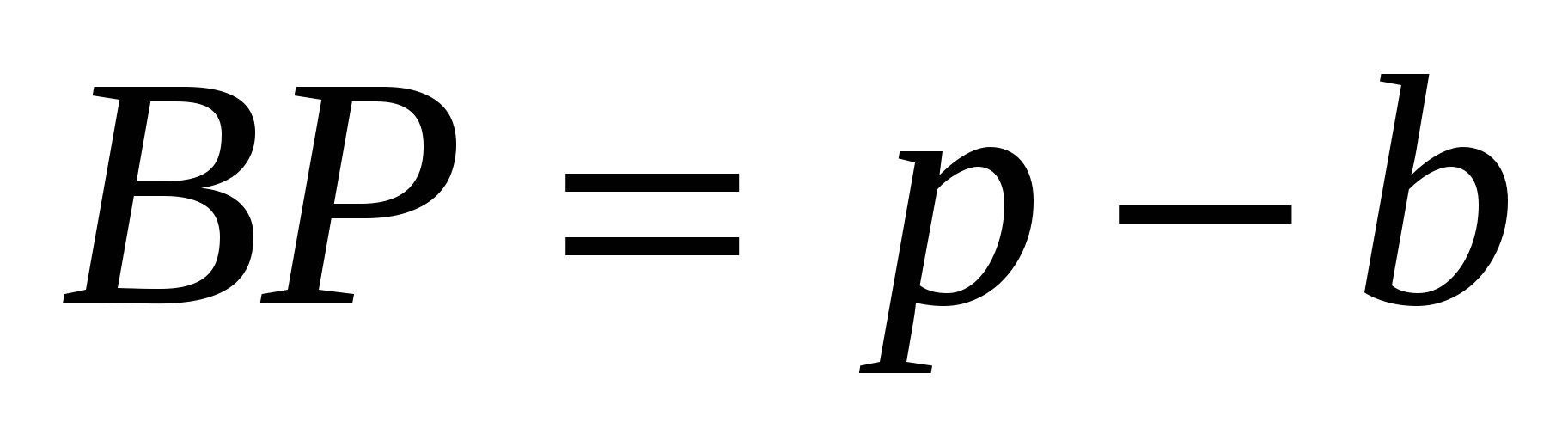

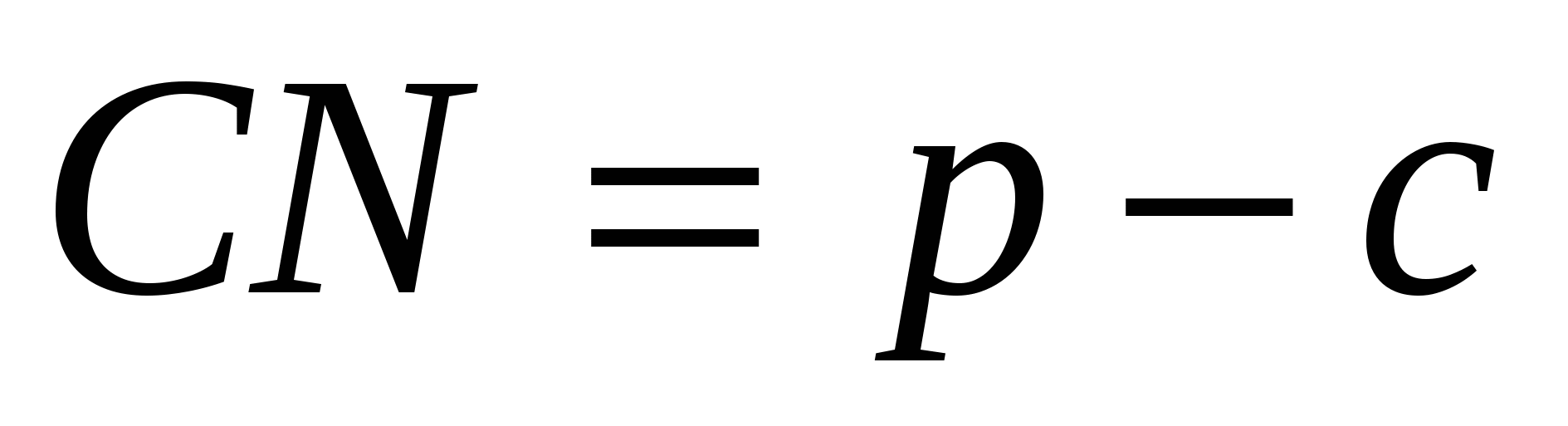
Задача 2. Дан треугольник АВС; a, b, c – его стороны. Найти длины отрезков, на которые делят стороны треугольника точки касания вневписанных окружностей.

Решение. Пусть AQ = у. Тогда AS = y, QC = CT = b — y, BS=BT, а поэтому

, .

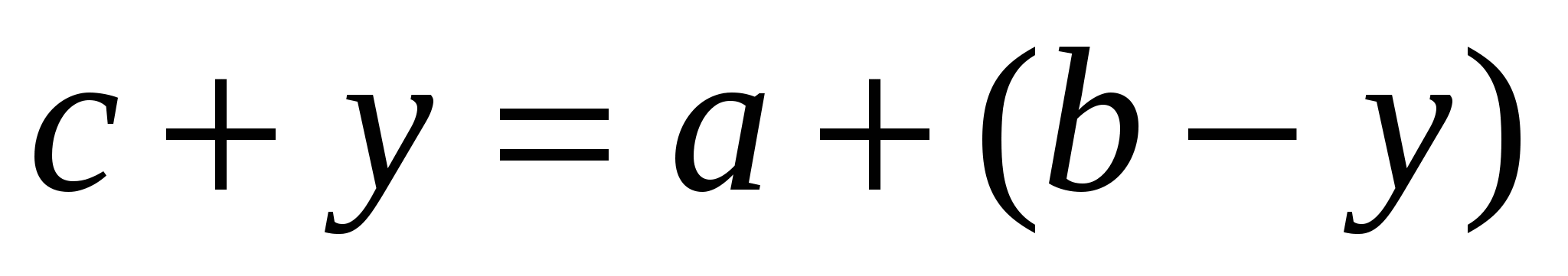
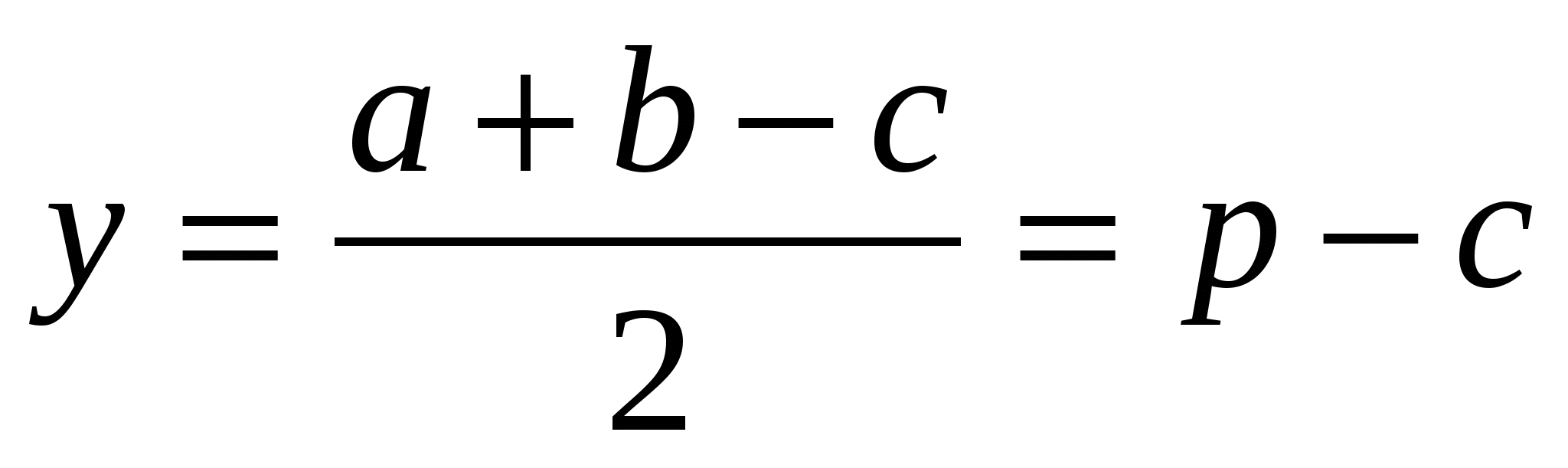
Аналогично можно вычислить и длины других искомых отрезков.

Переходим к выводу формулы Герона .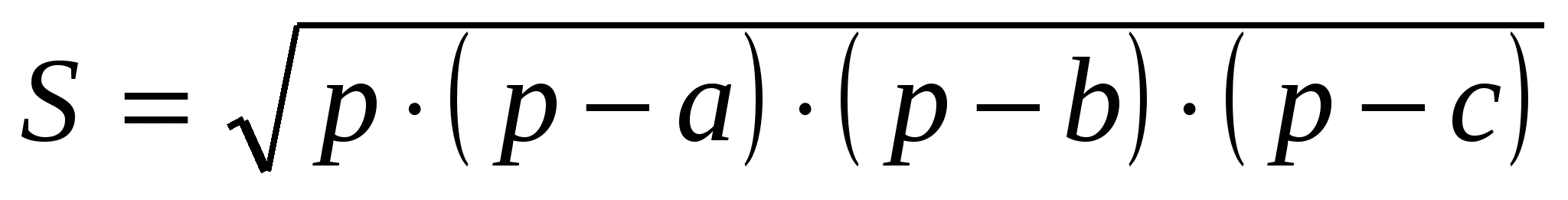

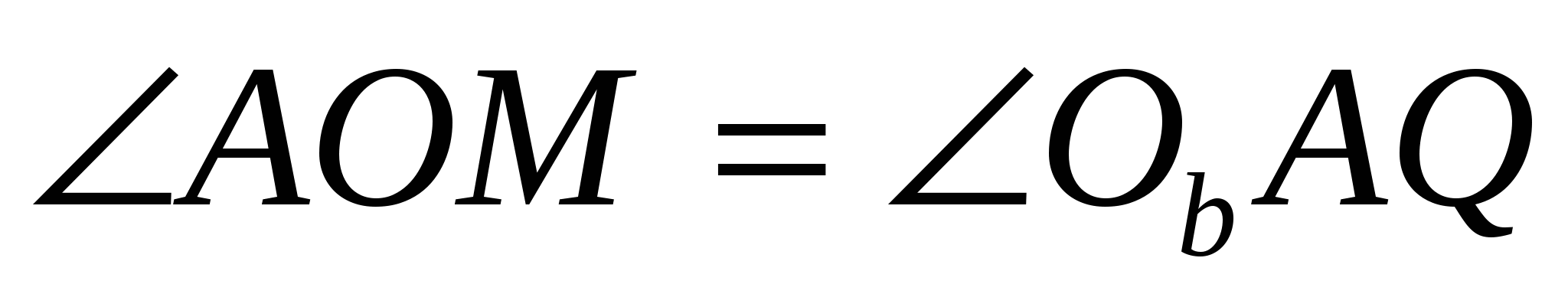
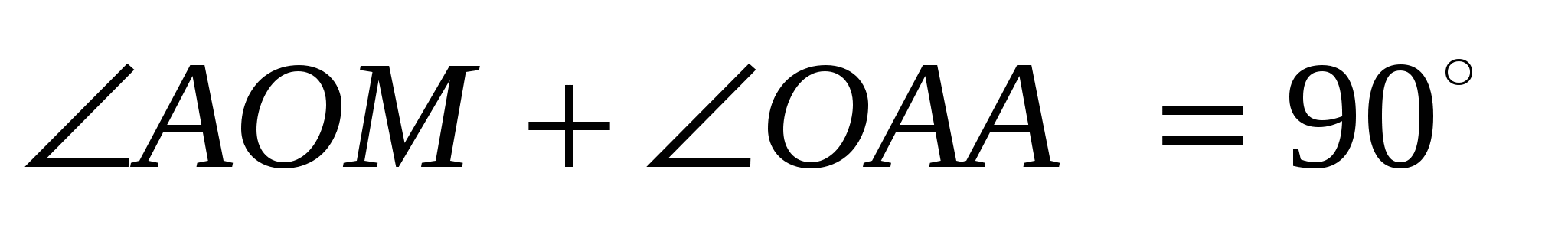
Доказательство. Треугольники АОМ и О_bAQ подобны, так как они прямоугольные и , как дополняющие угол ОАМ до прямого (как острые углы прямоугольного треугольника АОМ, , который равен 90  как угол, образованный биссектрисами двух смежных углов).

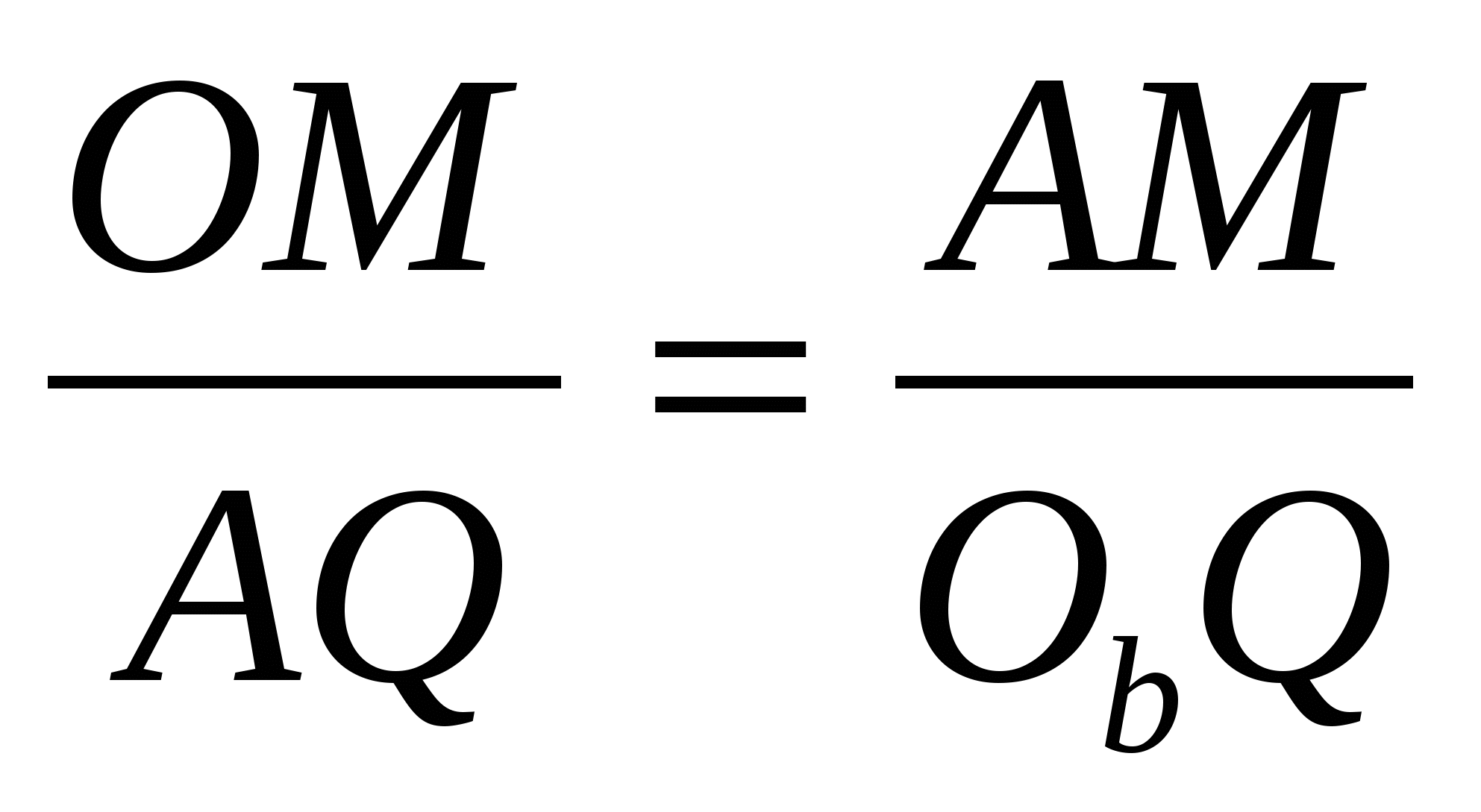
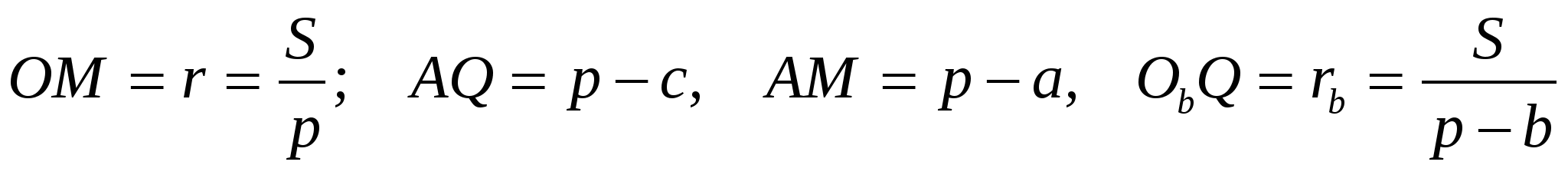
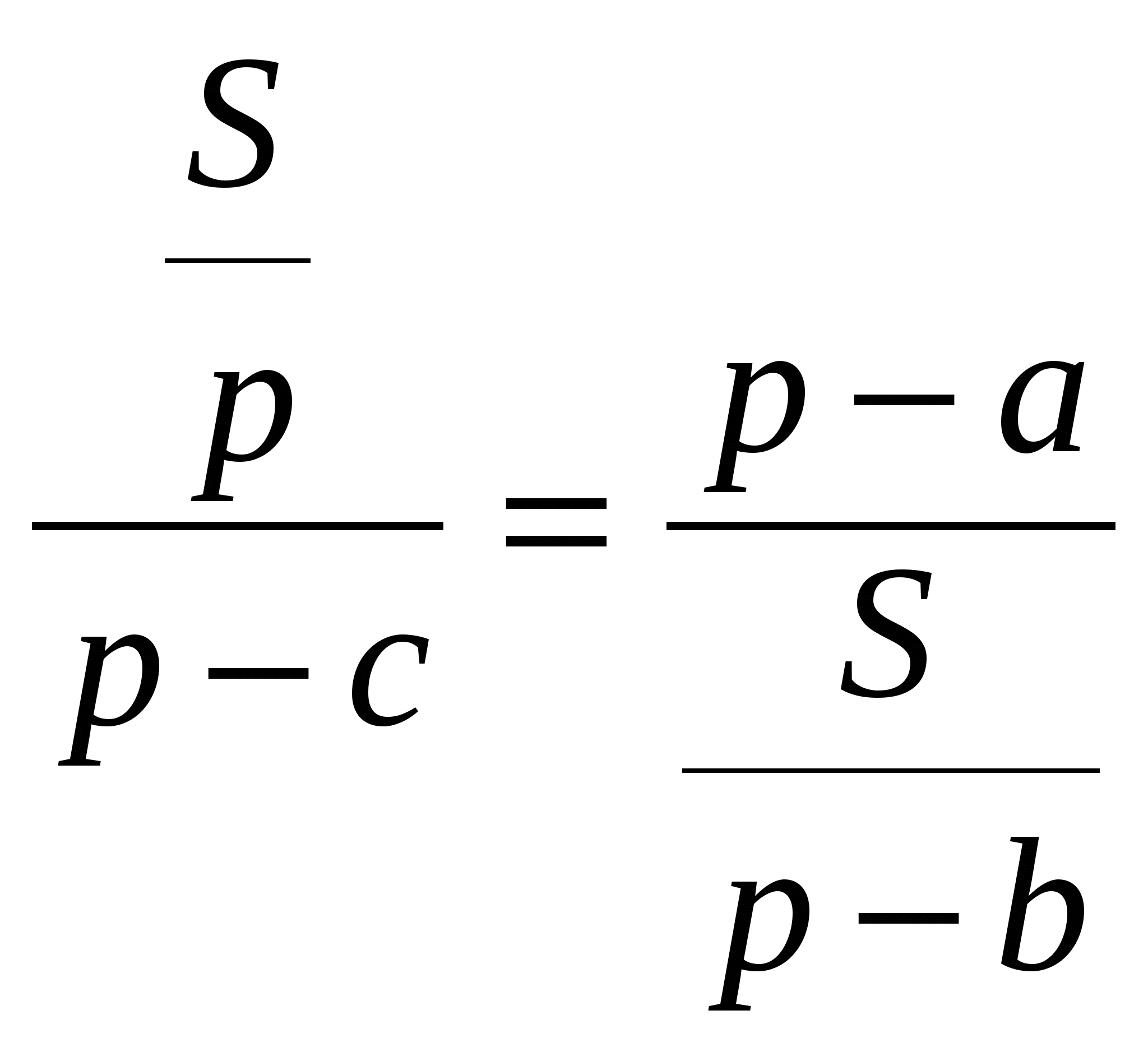
Из подобия треугольников АОМ и О_bAQ следует . После подстановки () получим .

Из этой пропорции следует справедливость формулы Герона: , , .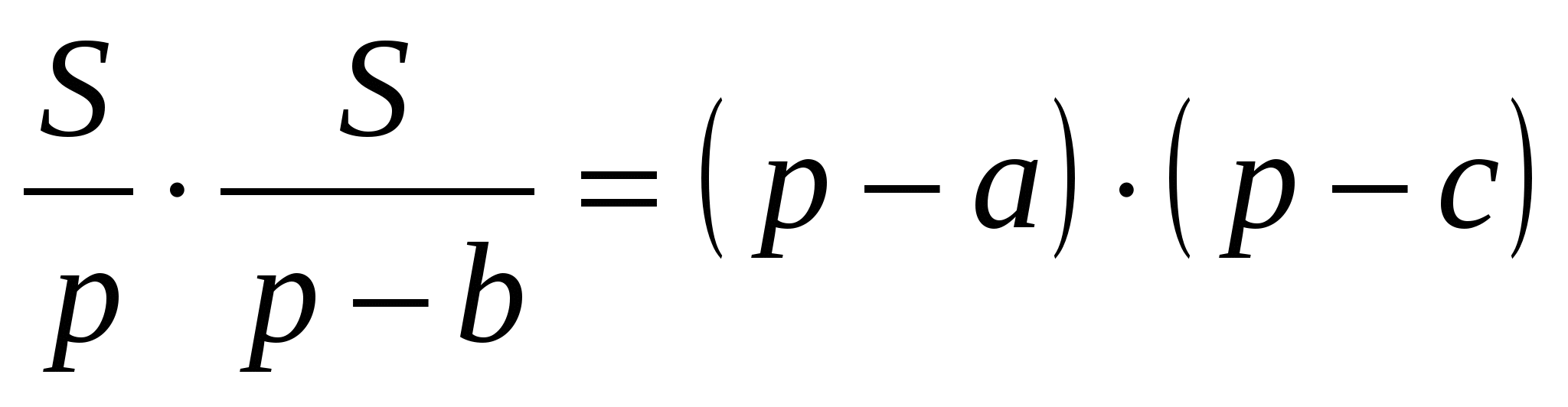

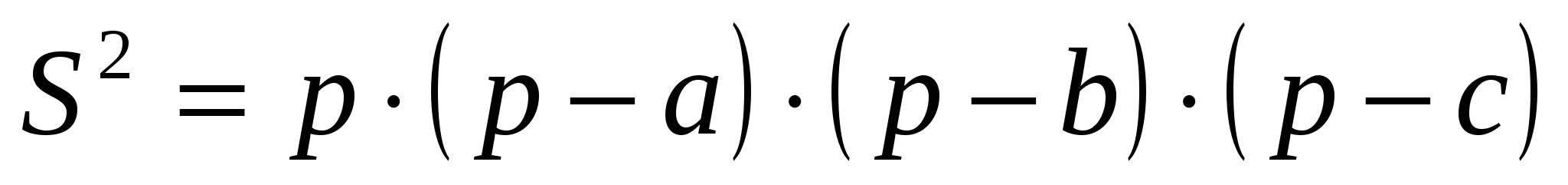
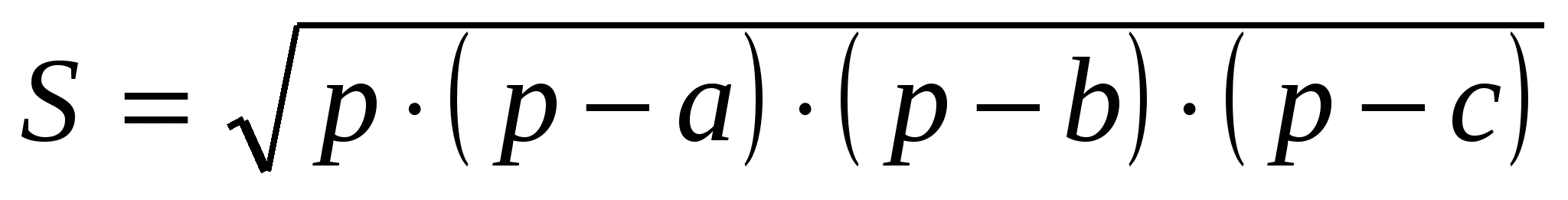
Так как и , то имеют место следующие соотношения между радиусами вписанной и вневписанной окружностей и .

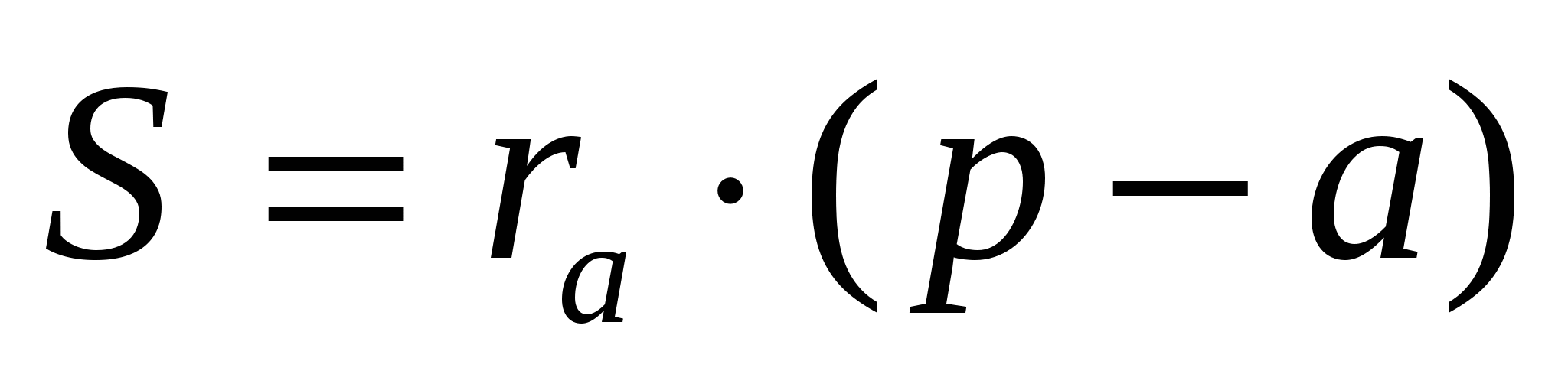
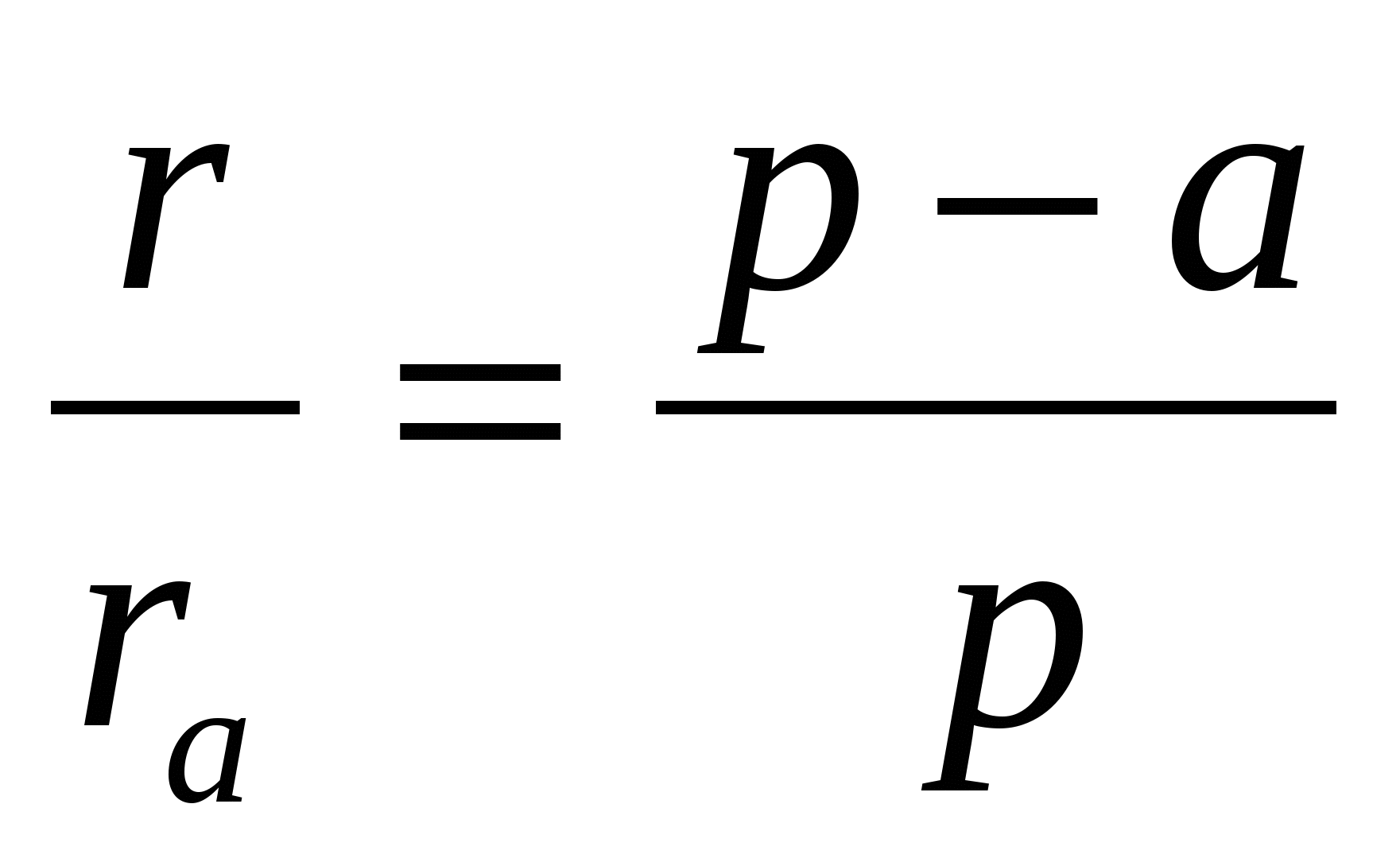
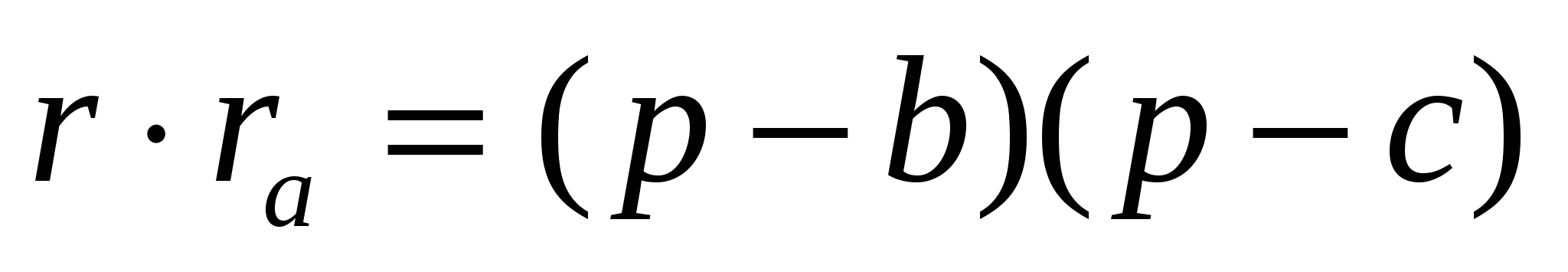
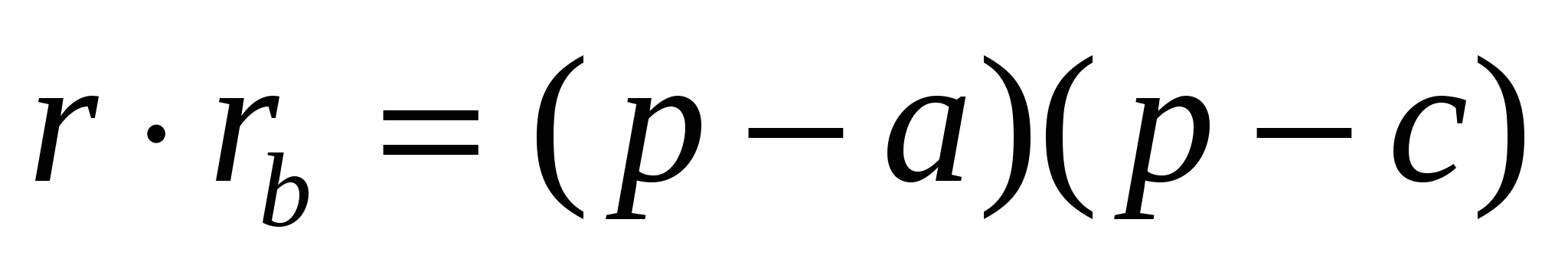
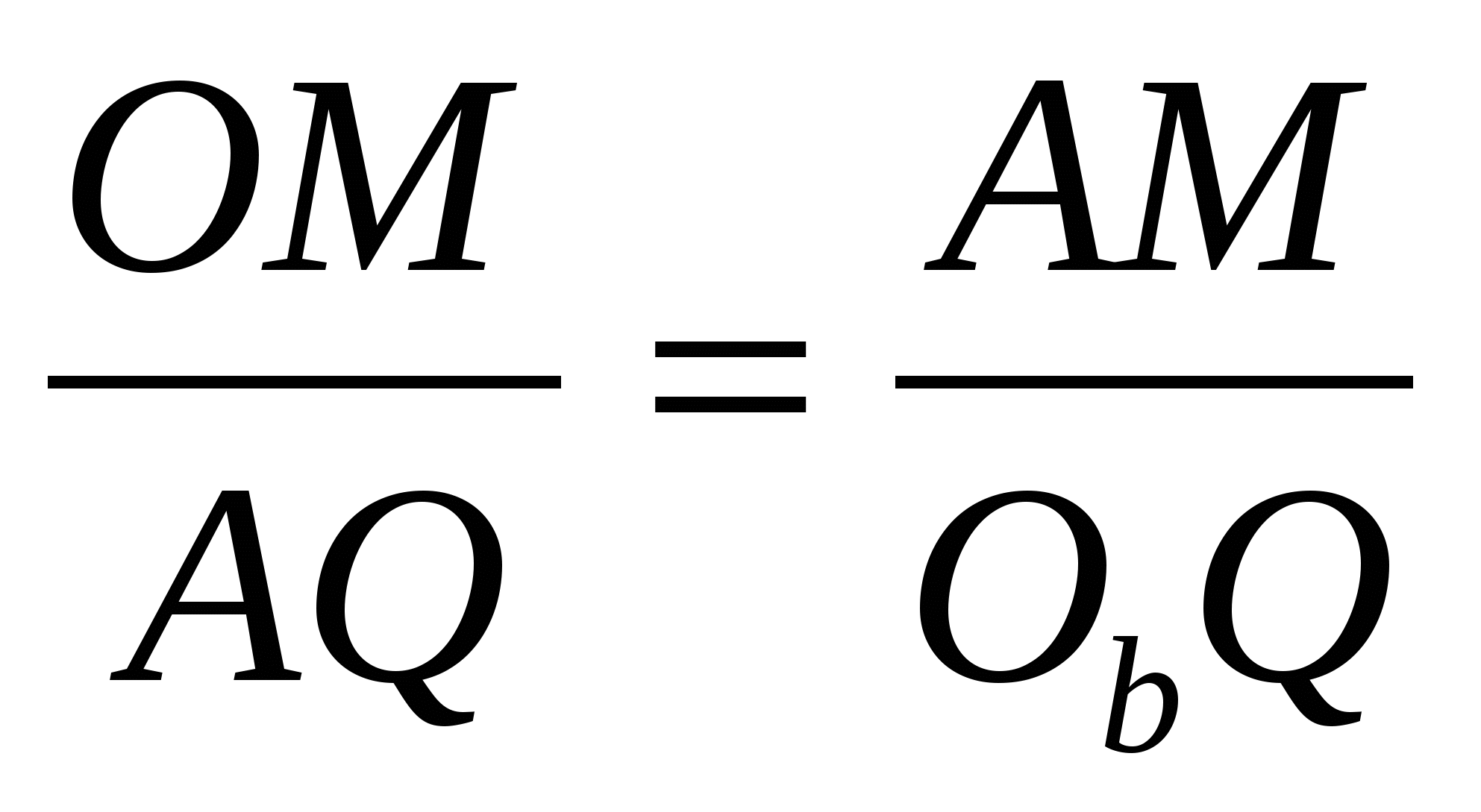
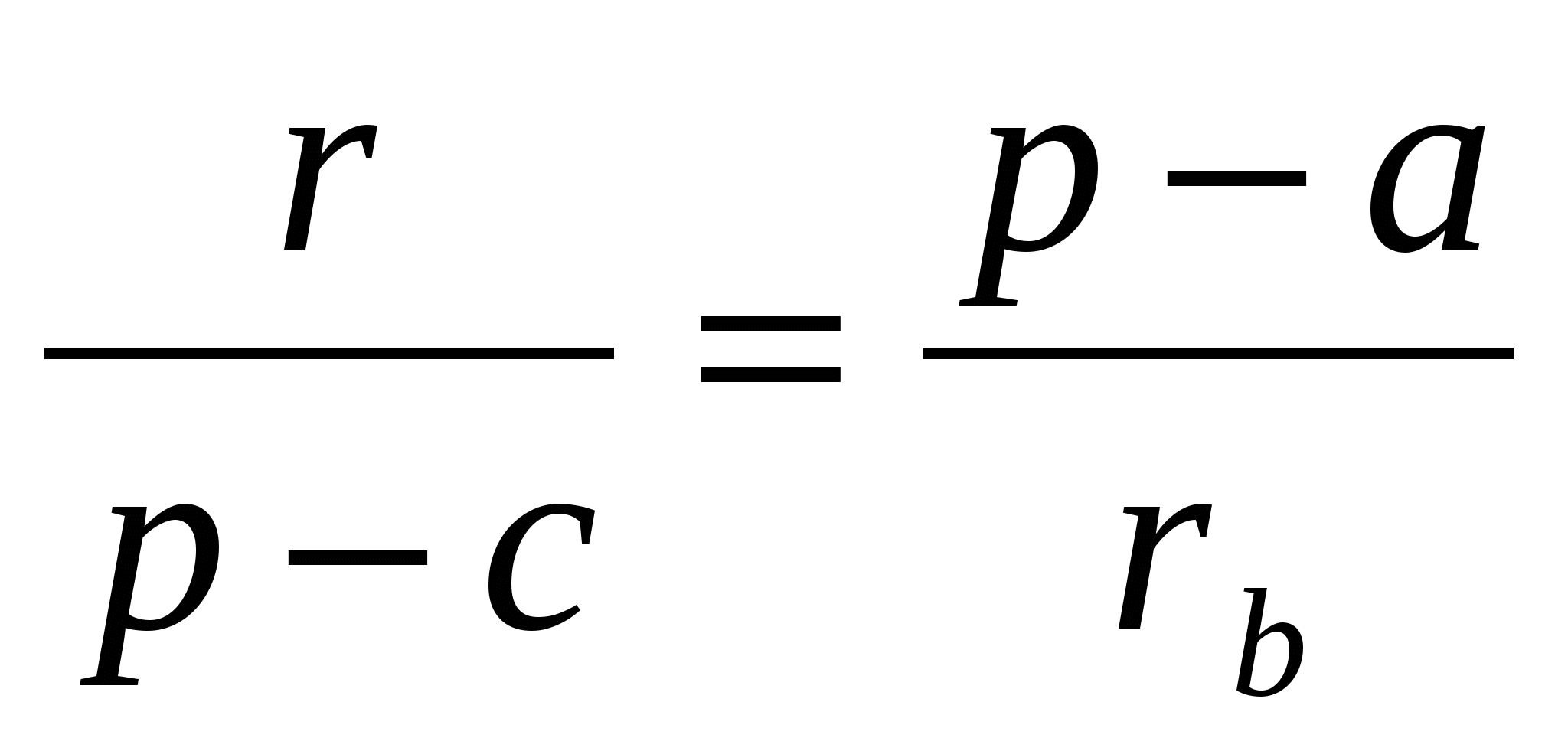
Для доказательства соотношения воспользуемся результатами выше рассмотренных задач и рис.11. Из подобия треугольников АОМ и О_bAQ следует . Таким образом , откуда следует справедливость равенства

Отметим еще одно свойство, которое вытекает из данных задач: (рис.11) если M и Q – соответственно точки касания вписанной и вневписанной окружности с их общей касательной АС, то АМ = CQ.

II . Применение свойств вневписанной окружности

к решению задач

1. Решение задач на доказательство

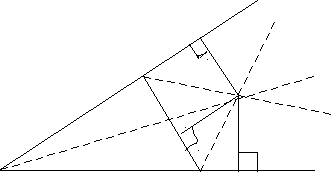
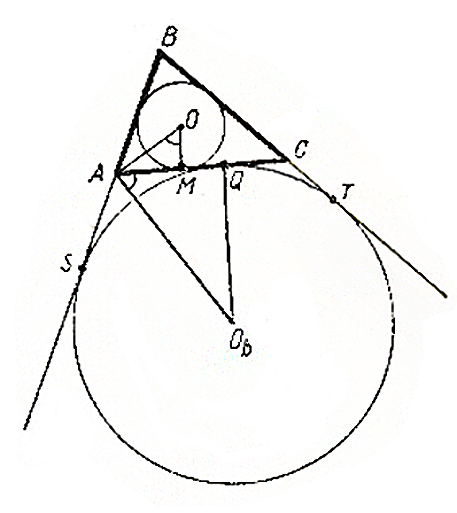
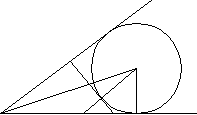
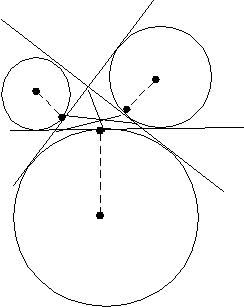
Задача 1. Две непересекающиеся окружности с радиусами R₁ и R₂ касаются сторон прямого угла с вершиной А. Общая внутренняя касательная с окружностями пересекает стороны угла в точках В и С. Найти площадь треугольника АВС.

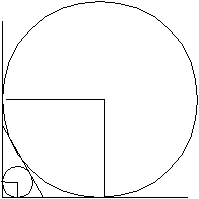
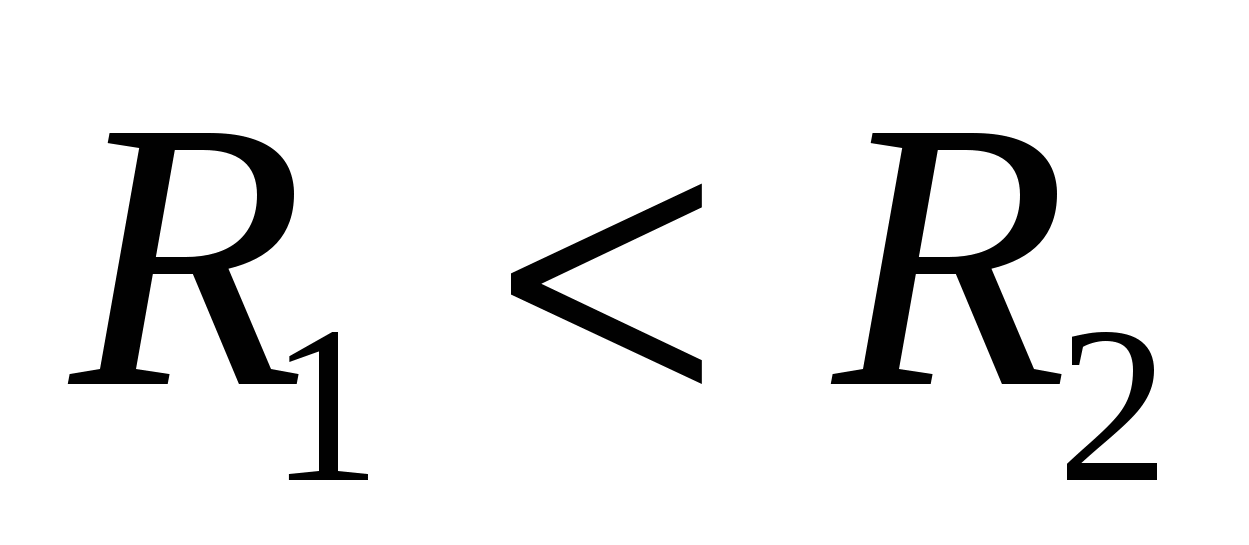
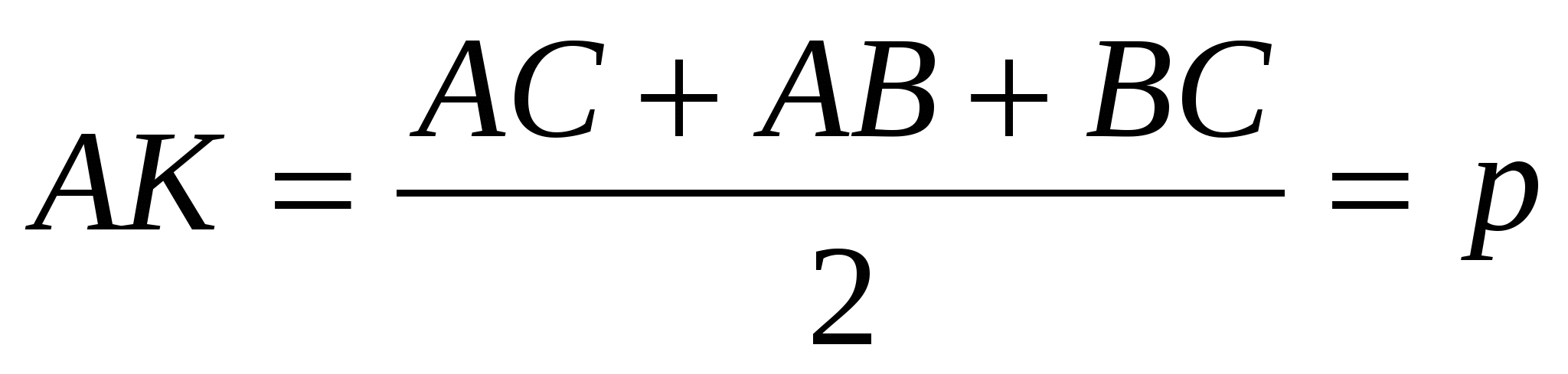
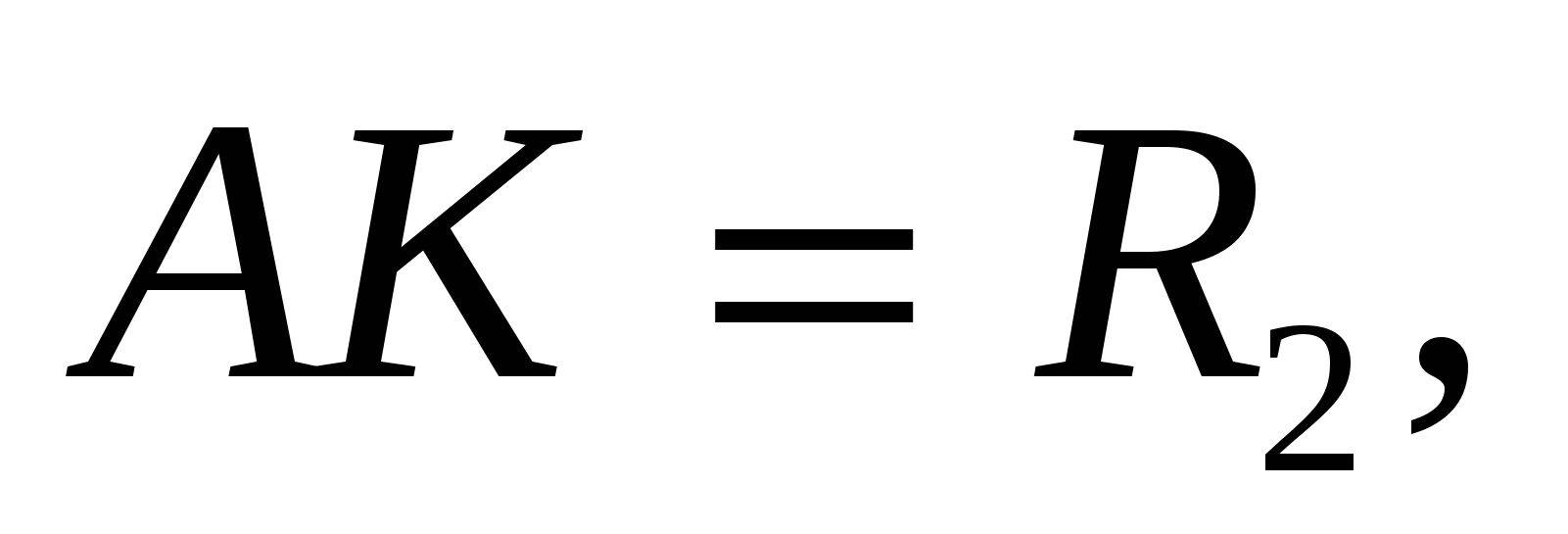
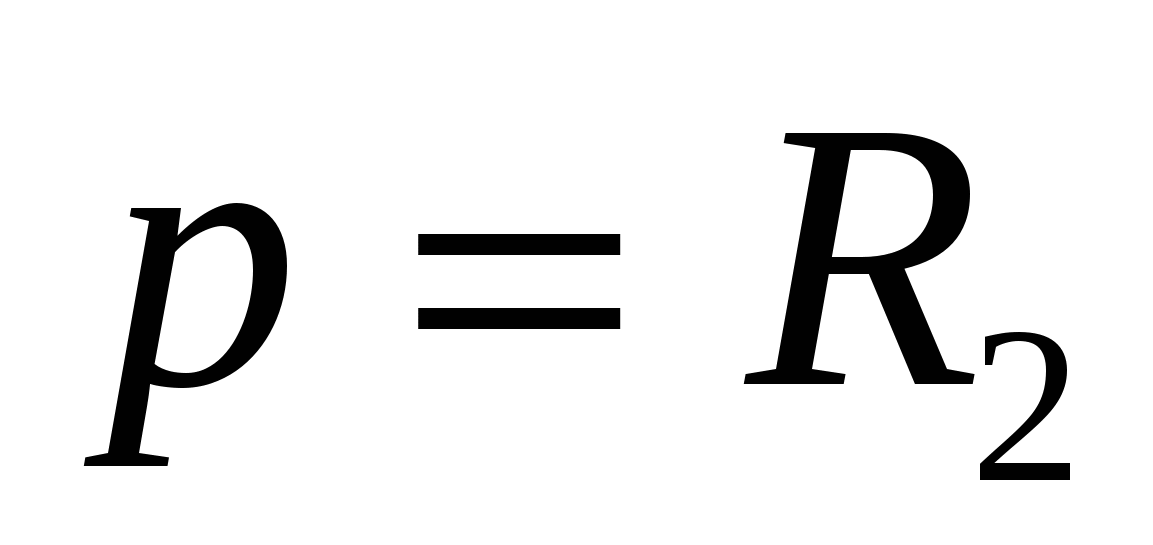
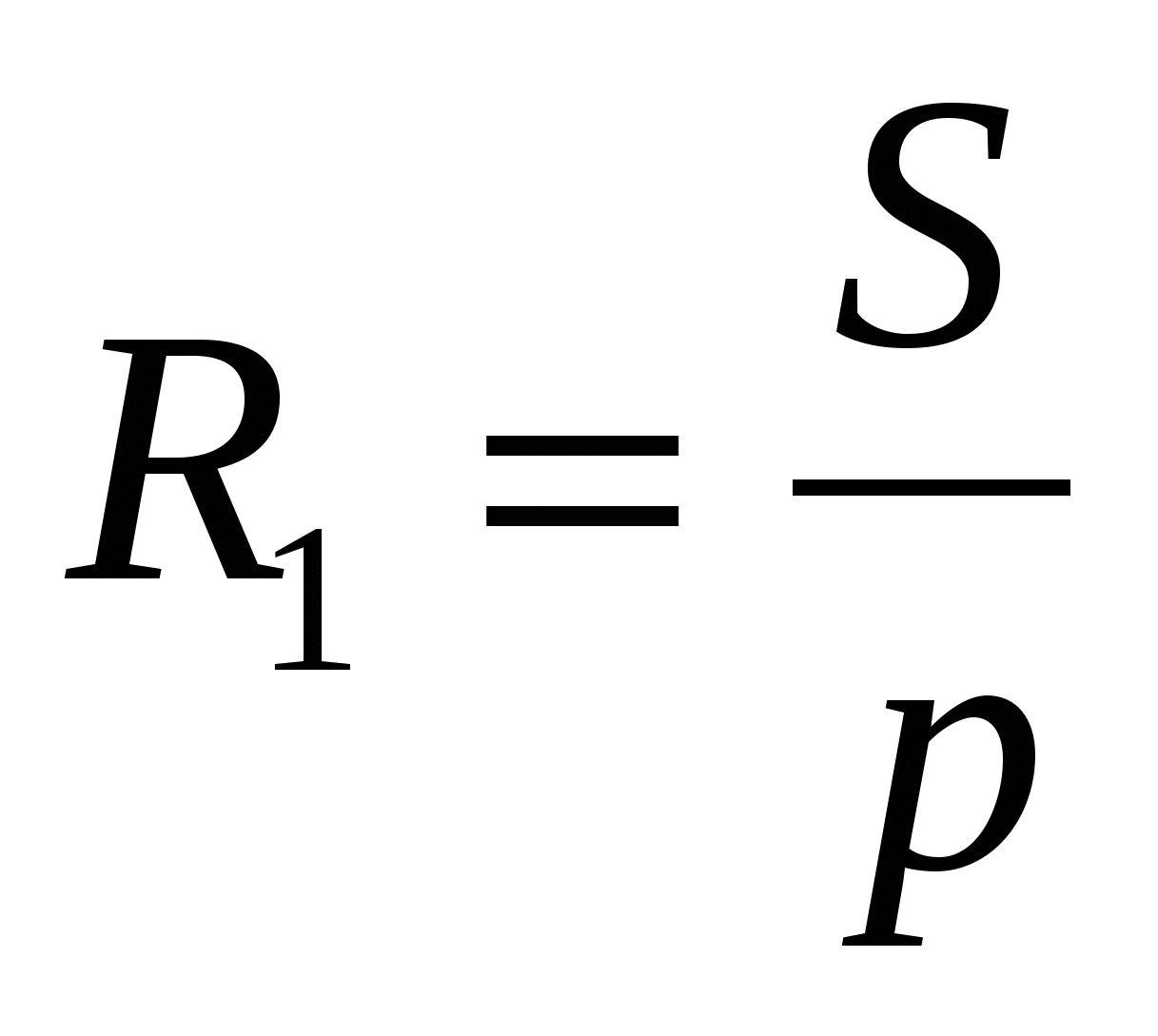
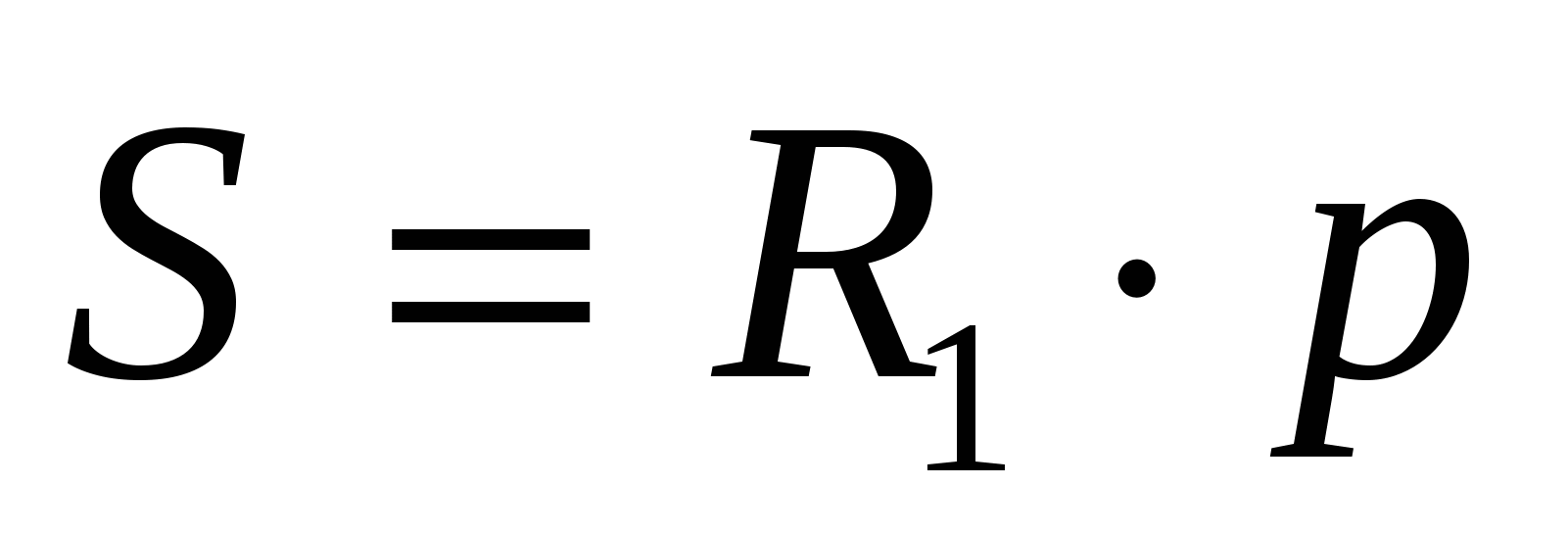
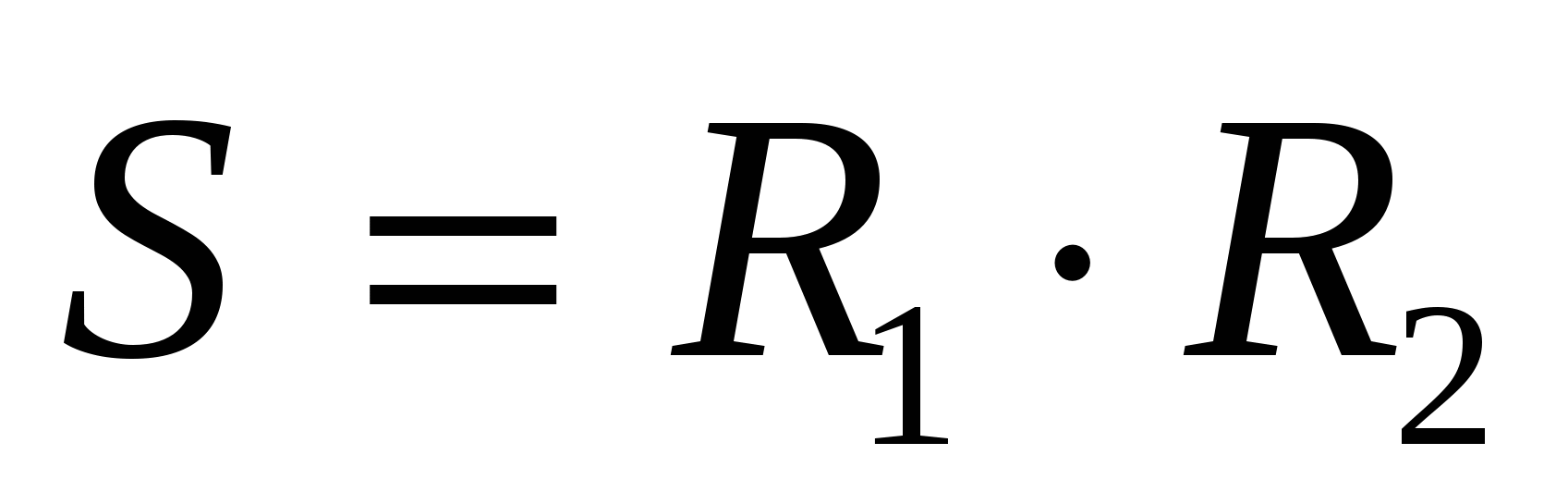
Решение. Так как обе окружности касаются сторон угла, то одна из них будет вписанной в треугольник АВС, а другая вневписанной. Пусть , где R₁ и R₂ – соответственно радиусы вписанной и вневписанной окружностей (рис.1). Если О– центр вневписанной окружности, а точки К и М – ее точки касания со сторонами угла А. Легко доказать, что АКОМ – квадрат со стороной R₂. По теореме 2 . Но так как то . А . Отсюда следует , .

Ответ: площадь треугольника равна

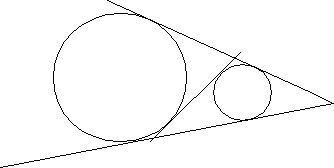
Задача 2. К двум непересекающимся окружностям проведены две общие внешние касательные и общая внутренняя касательная. Докажите, что отрезок внутренней касательной, заключенный между внешними касательными, равен отрезку внешней касательной, заключенному между точками касания.

Р

ешение. Пусть даны две окружности. Точки касания окружностей с первой внешней касательной – А и В, со второй – С и D (рис 2.) Внутренняя касательная пересекает внешние в точках М и N . Продолжим прямые АВ и С D до их пересечения в точке К. Тогда окружность с центром О₂ является вписанной в треугольник М NK , а окружность с центром О₁— вневписанной. Обозначим сторону М N треугольника MNK через а и его полупериметр через р. Тогда (по т.2.) АК = р и ВК = р – а. Значит, АВ = а, т. е. АВ = М N . Аналогично CD = MN.

Задача 3. В равнобедренном треугольнике с основанием 12 вписана окружность, к ней проведены три касательные так, что они отсекают от данного треугольника три малых треугольника. Сумма периметра малых треугольников равна 48. Найдите боковую сторону данного треугольника.

А

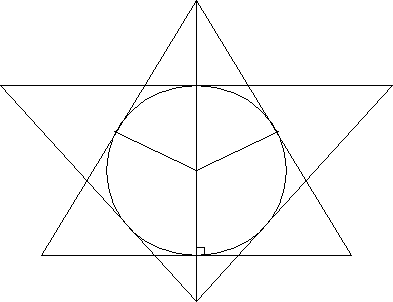
1.

2. Окружность с центром О – вневписанная окружность треугольников Е A L, BKF и PDC .

Поэтому , , , , ,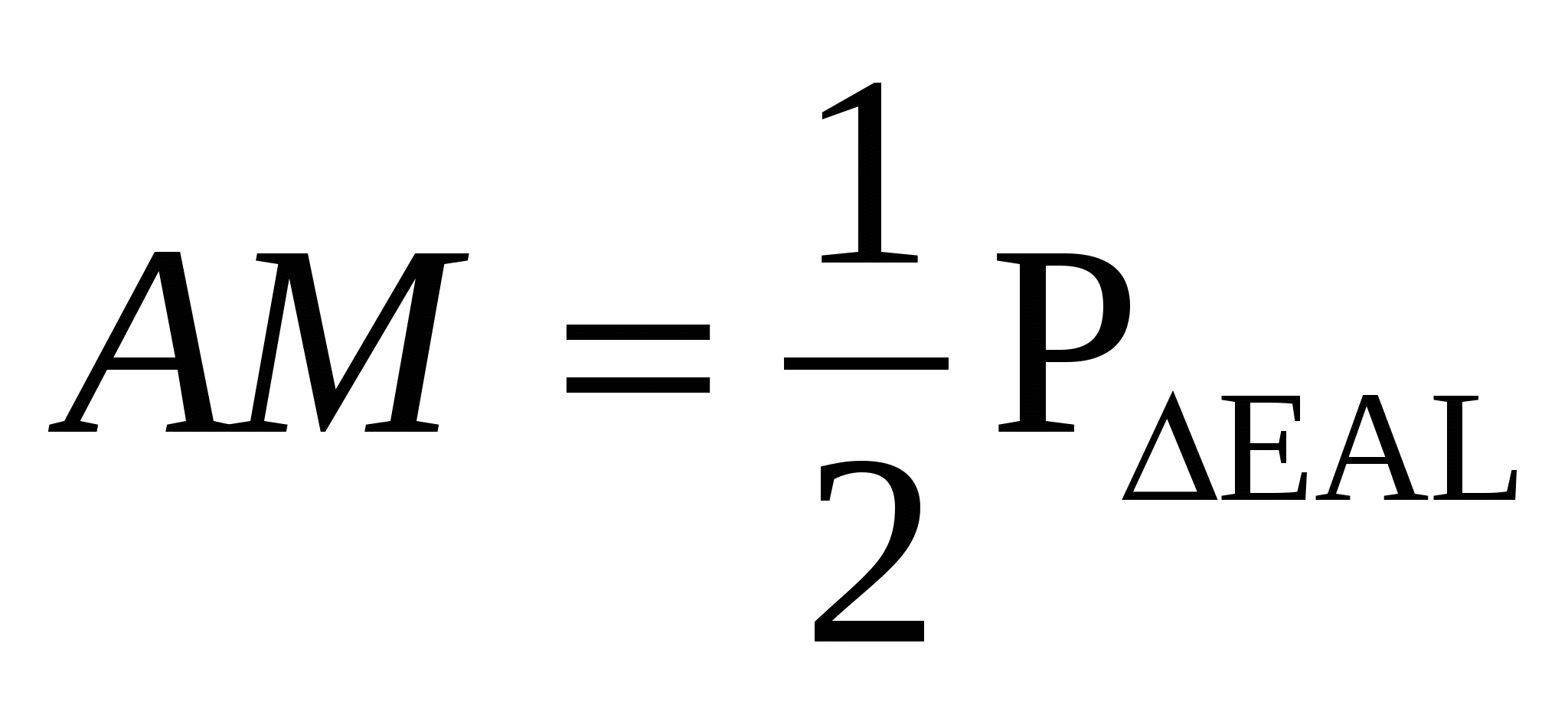

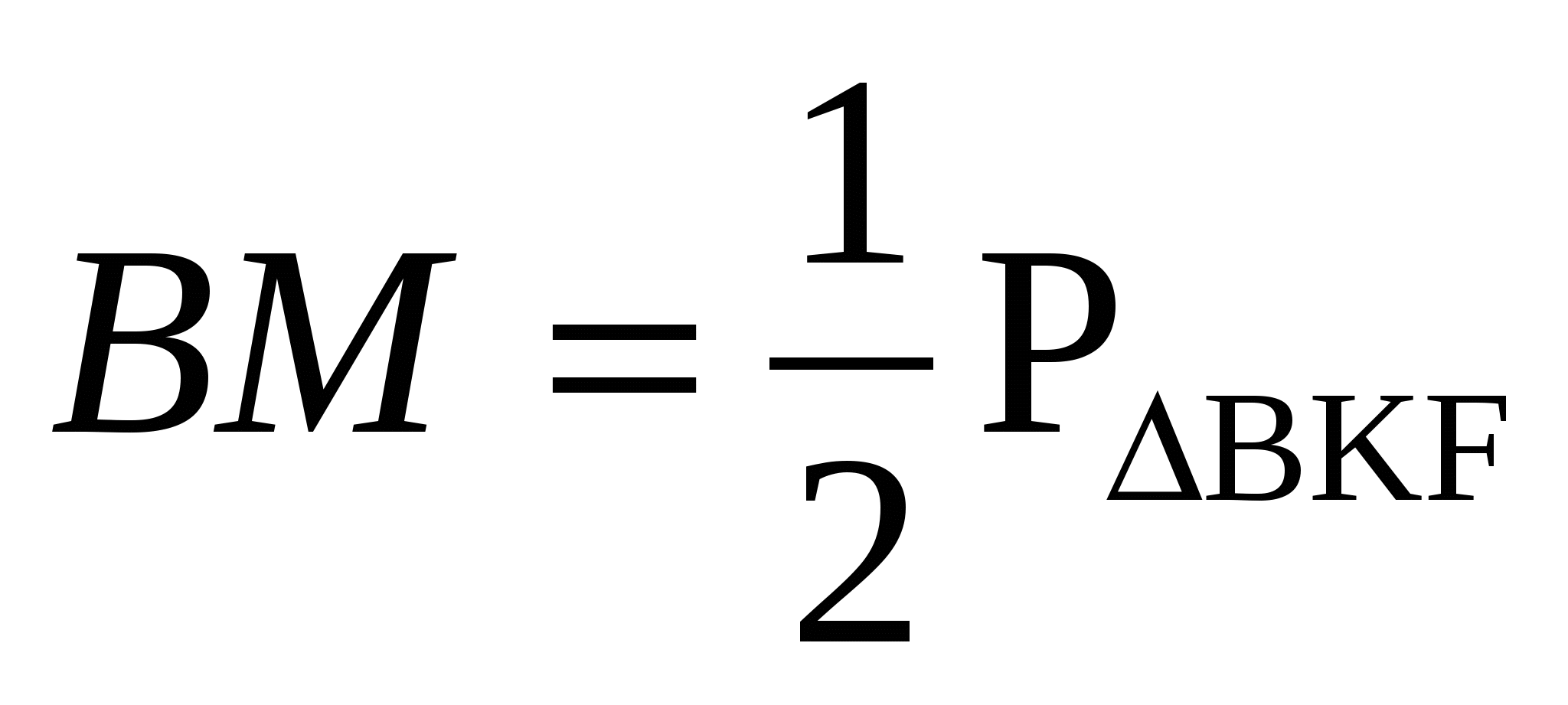
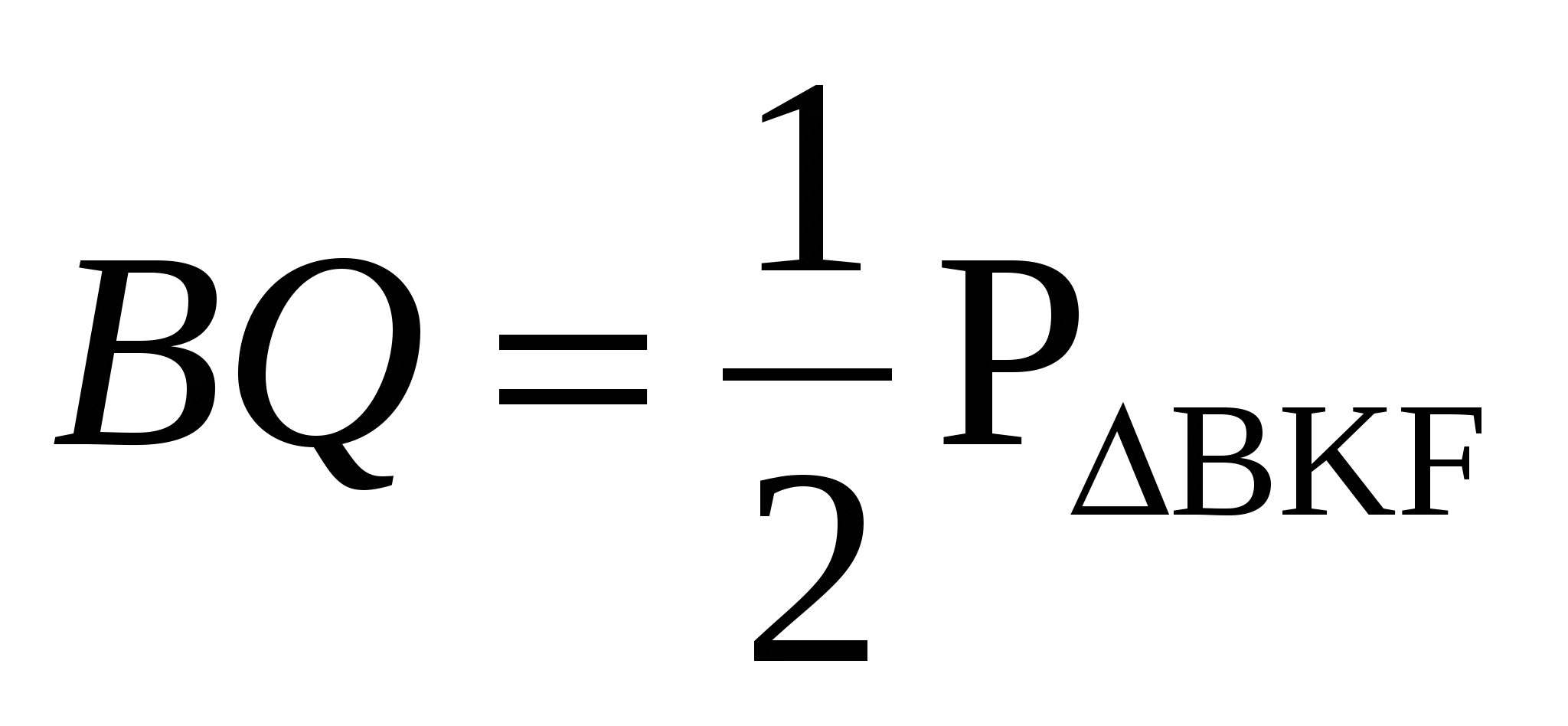
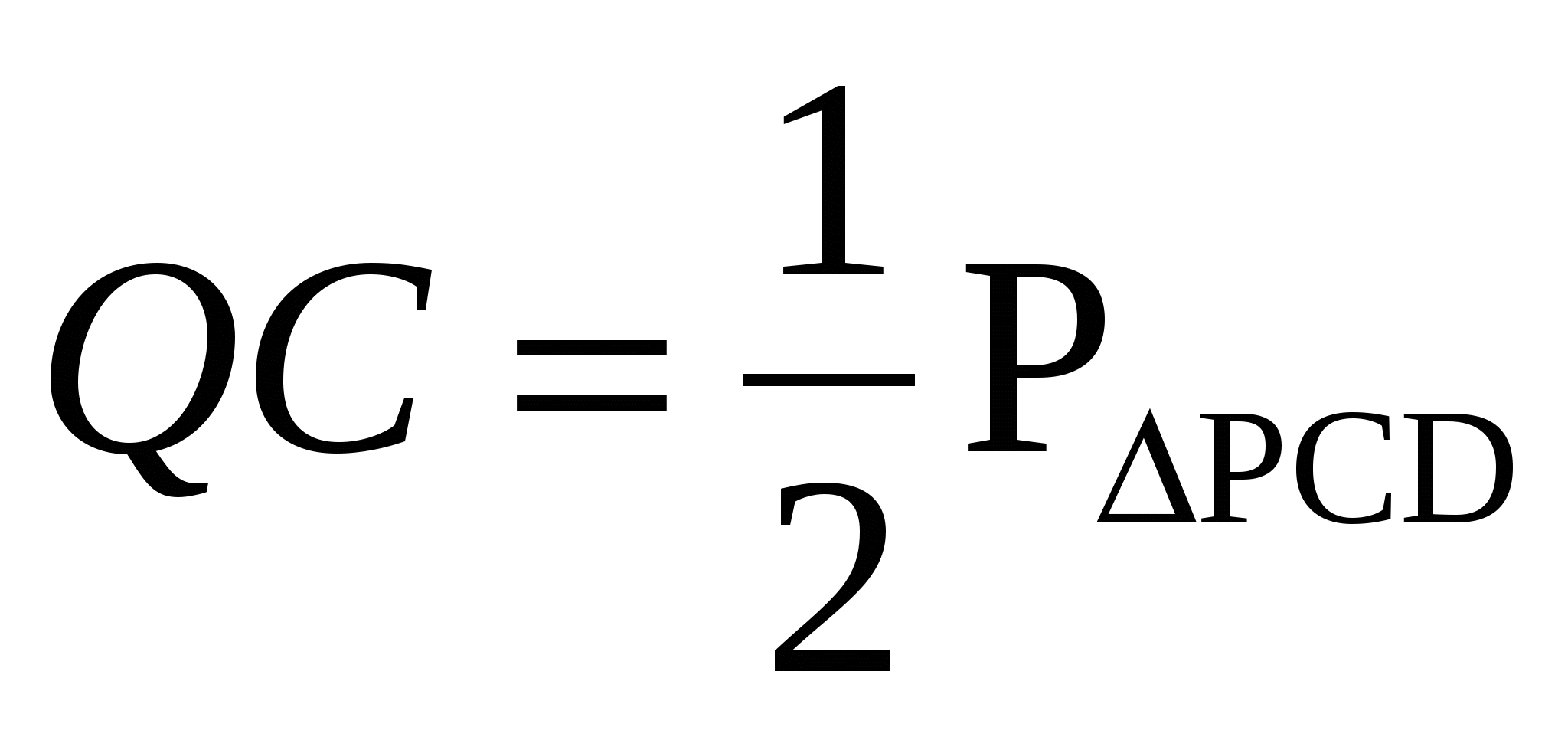
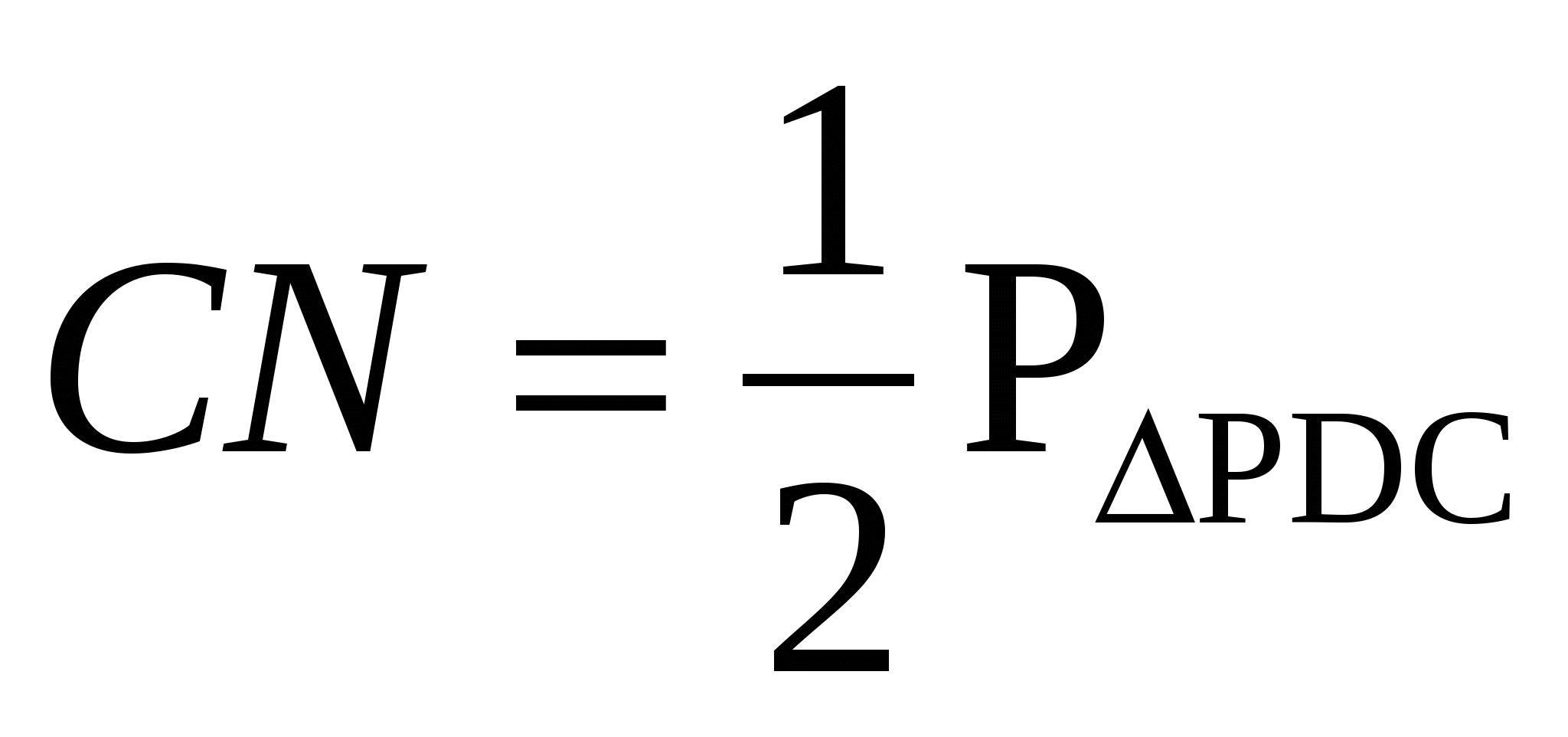
Из этого следует, что .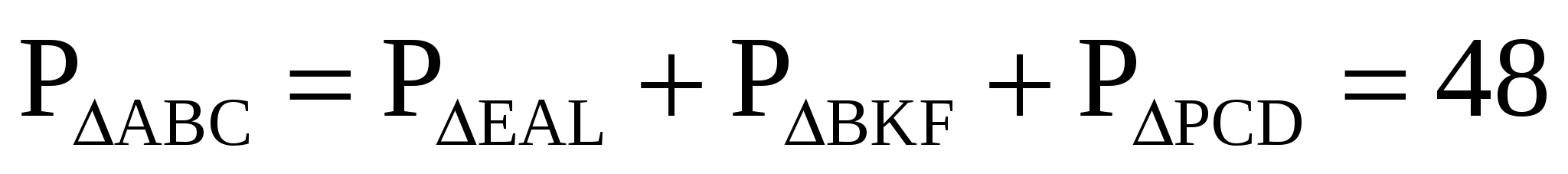

Значит, .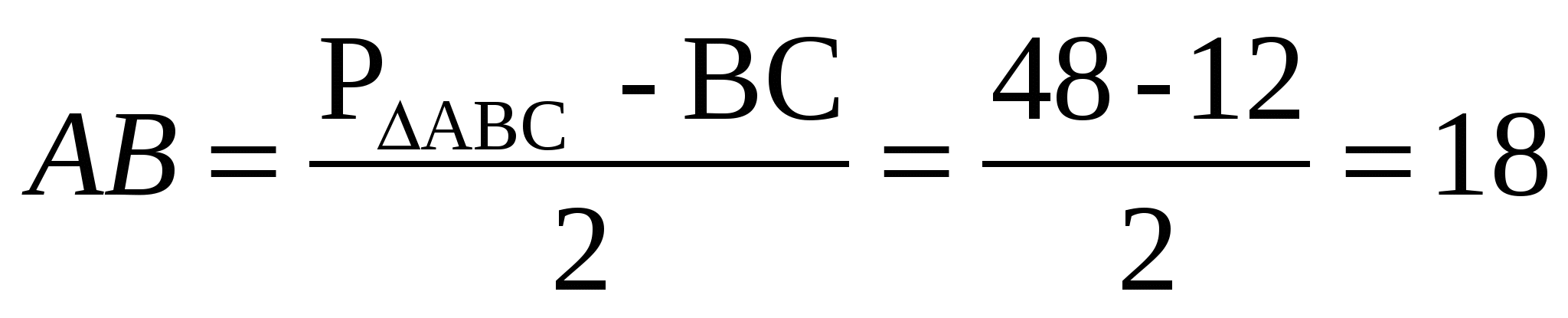

Задача 4. Прямые РА и РВ касаются окружности с центром О ( А и В – точки касания). Проведена третья касательная к окружности, пересекающая отрезки РА и РВ в точках Х и У. Докажите, что величина угла ХОУ не зависит от выбора третьей касательной.

Р

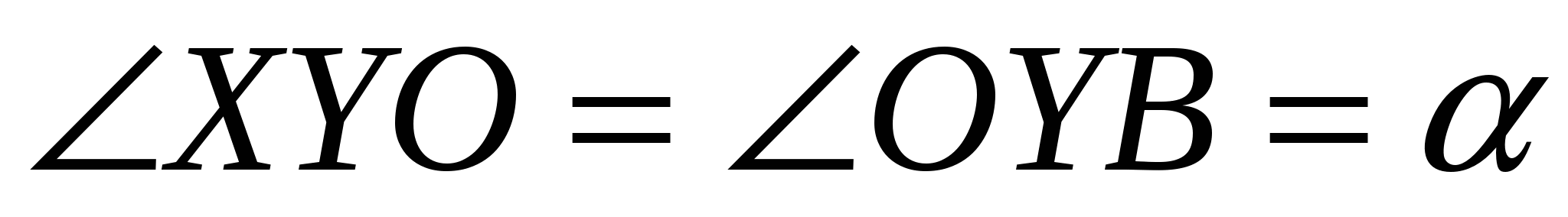
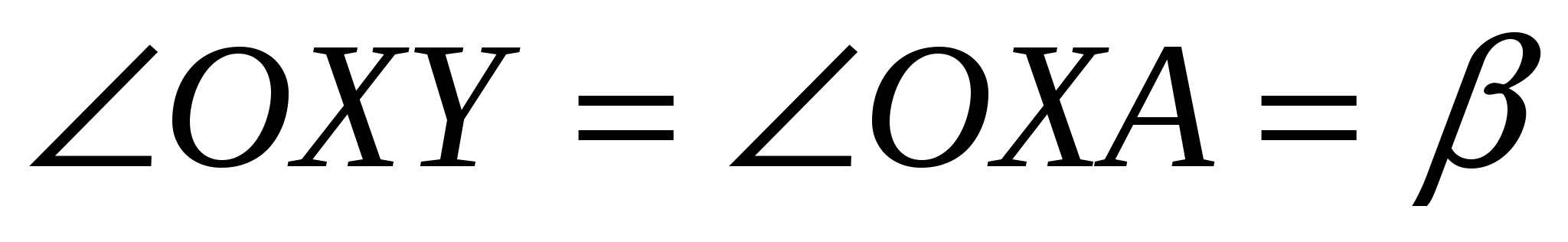
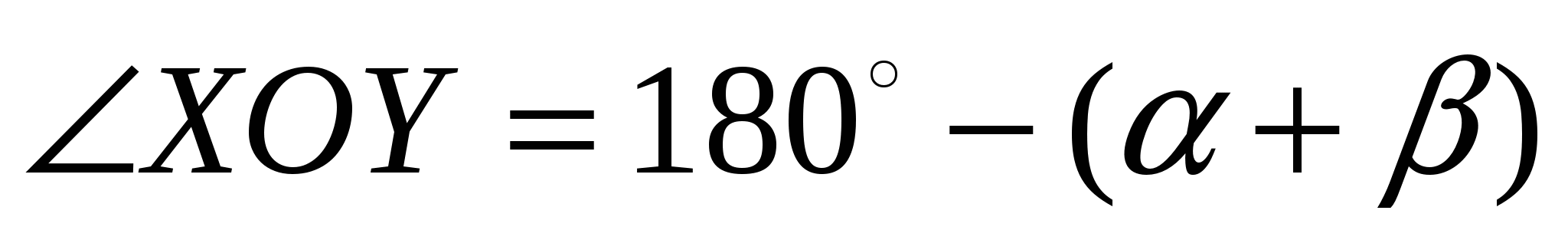
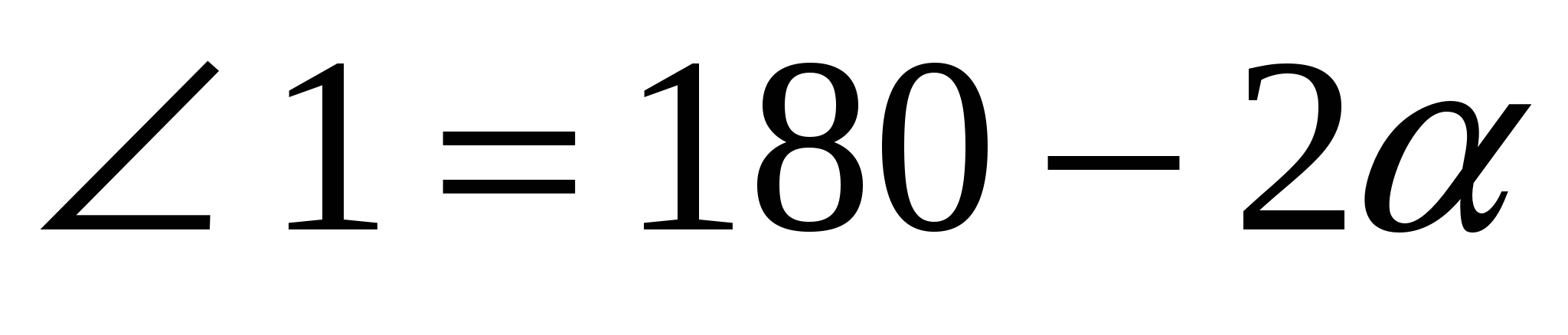
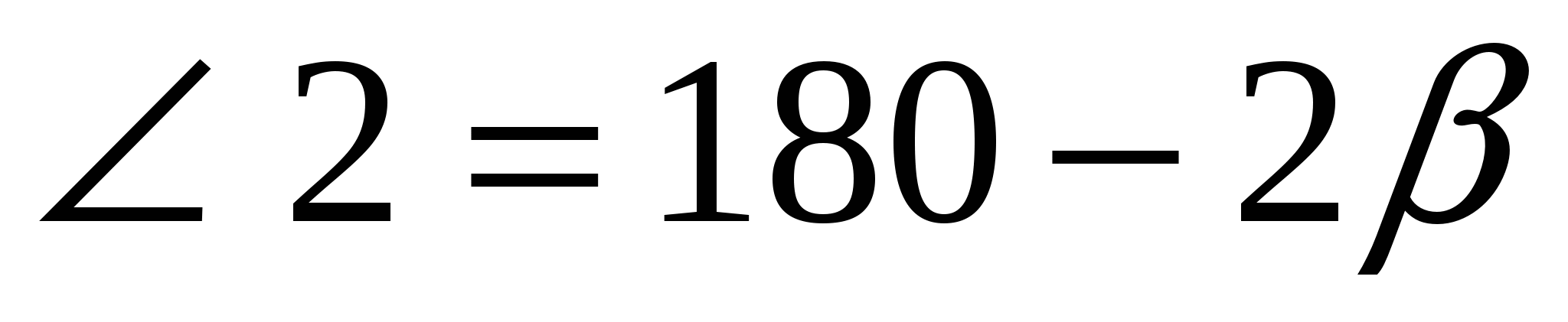
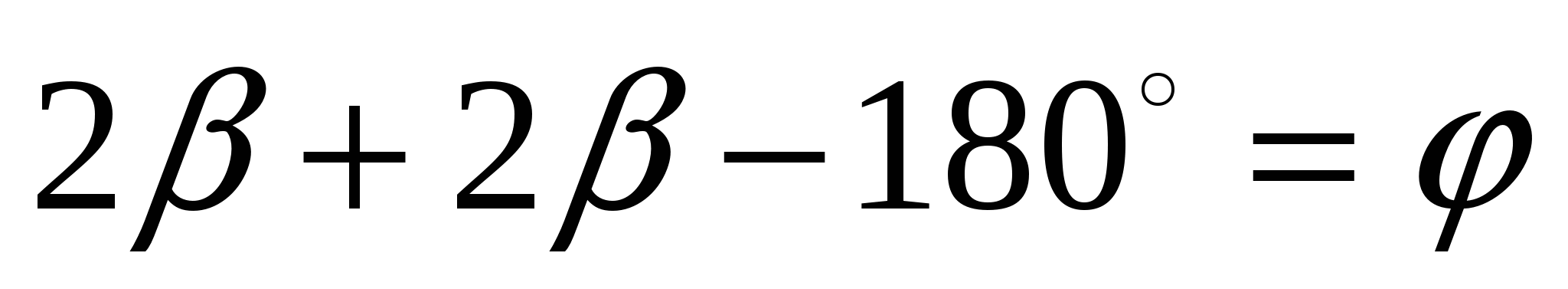
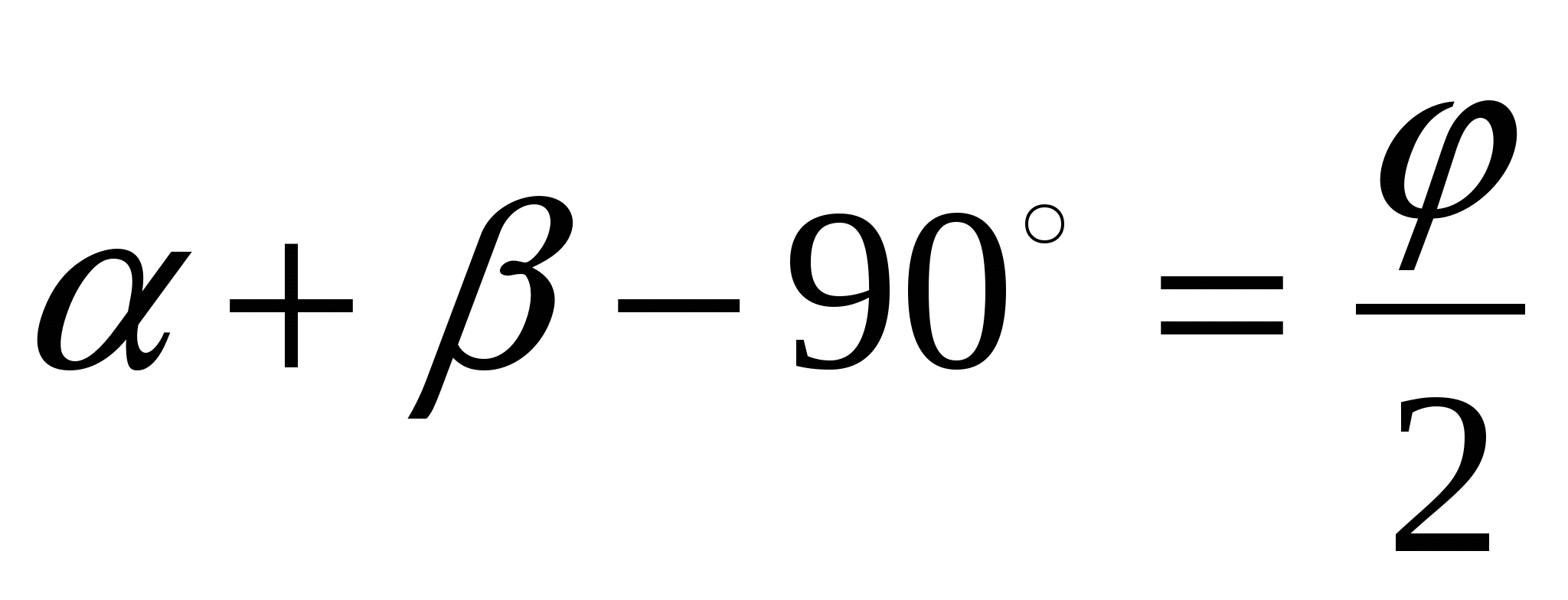
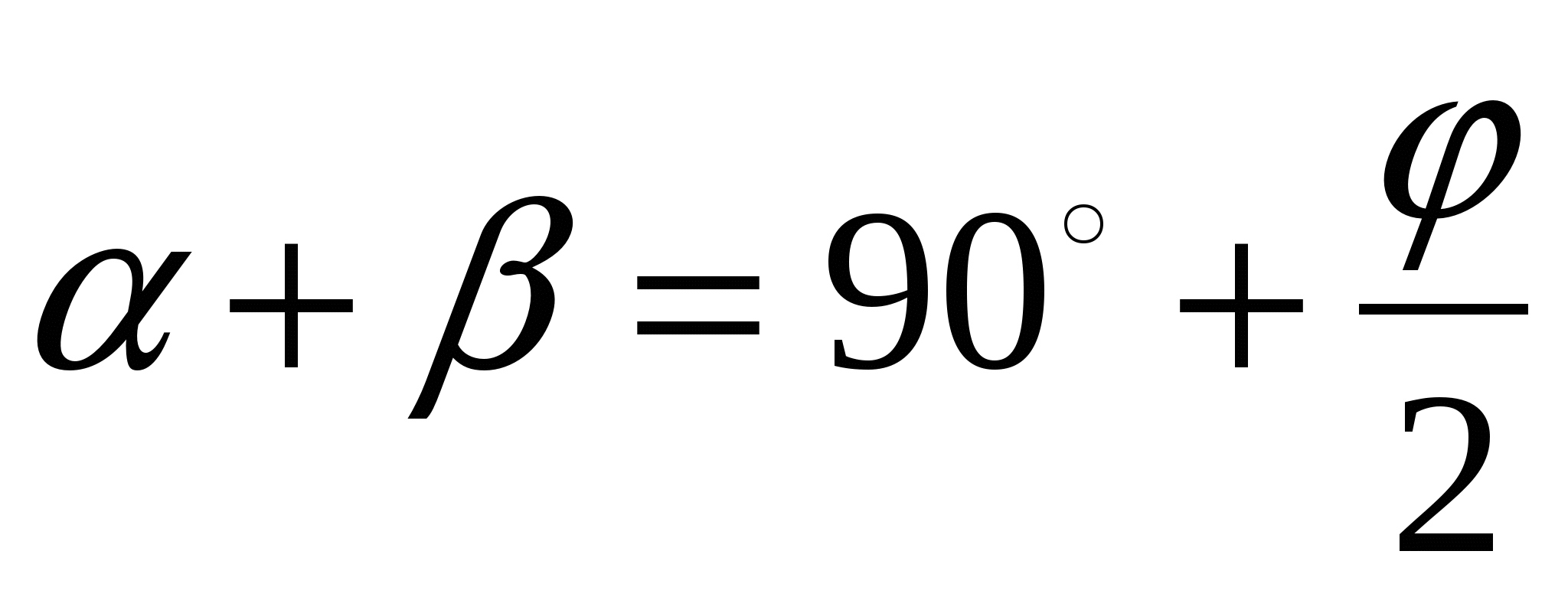
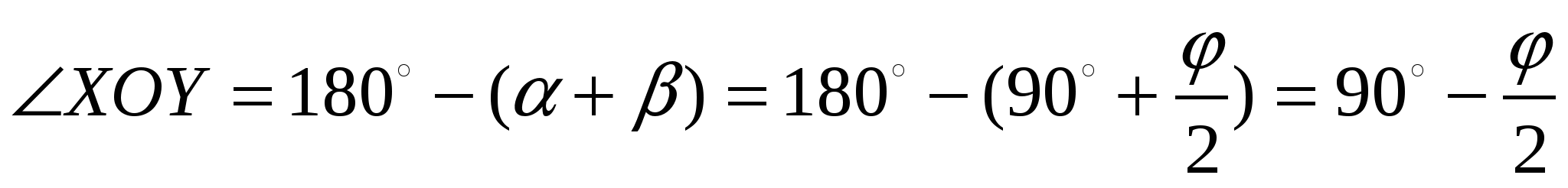
ешение. Так как касательные РА и РВ пересекаются, то угол АРВ обозначим  . Точки Х и У лежат соответственно на отрезках РА и РВ, поэтому данная окружность будет вневписанной для треугольника ХРУ. Центр окружности лежит на пересечении биссектрис, значит , . Величина угла ХОУ соответственно равна. В треугольнике РХУ , . Величина угла АРВ заданная, тогда имеем:, , . Величина угла ХОУ соответственно равна: и не зависит от выбора третьей касательной.

Задача 5. Доказать, что .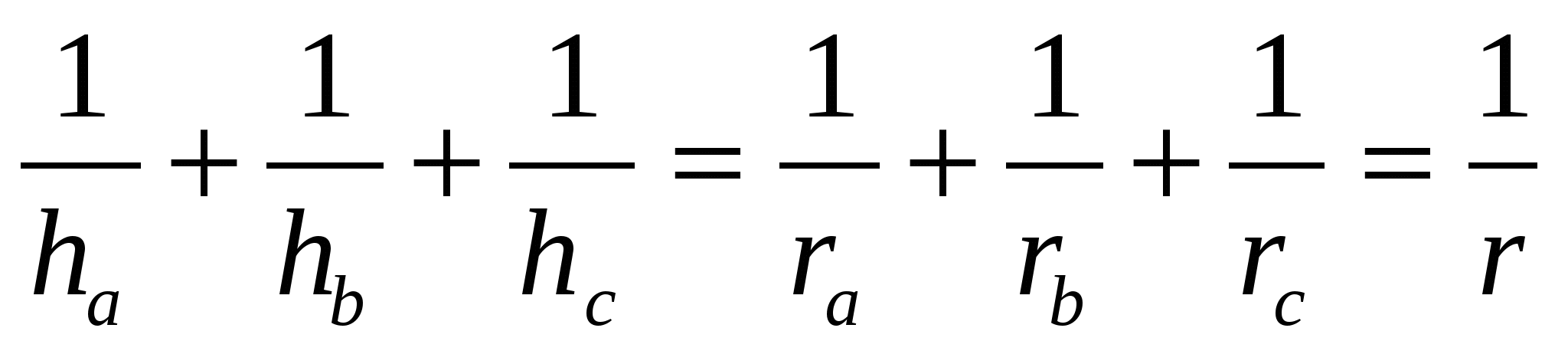

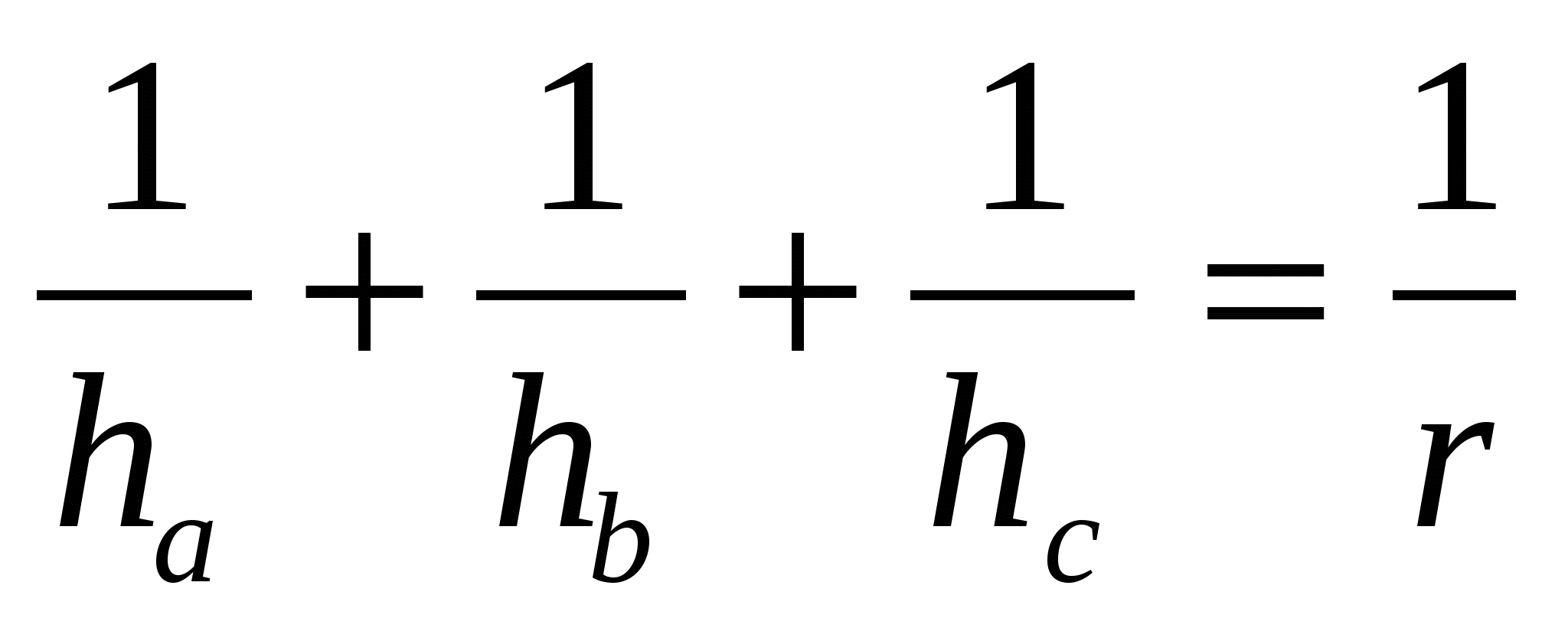
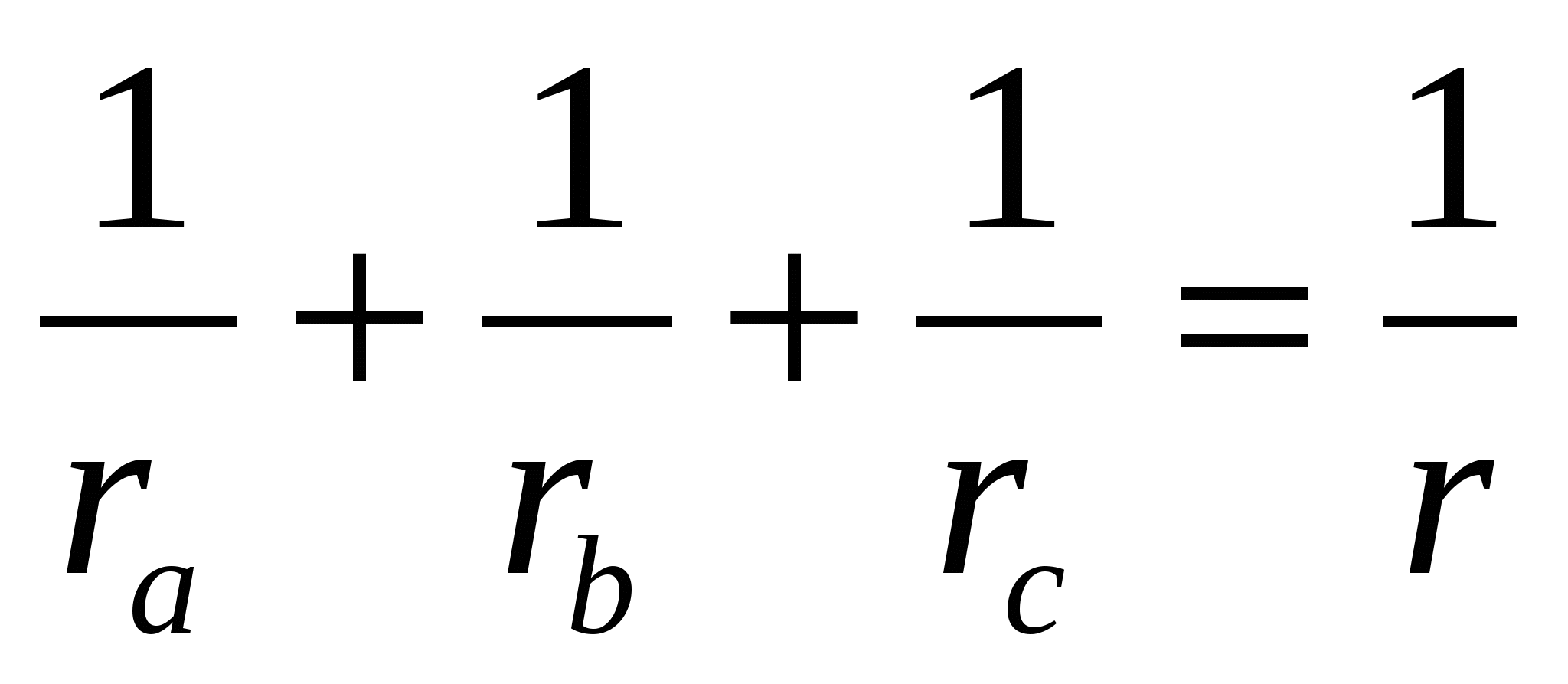
Доказательство. Воспользуемся тем, что радиус вписанной окружности связан с высотами треугольника соотношением . А по следствию из теоремы 4 о среднем гармоническом радиусов вневписанных окружностей треугольника имеем . На основании этих двух равенств и следует справедливость исходного равенства.

Задача 6. Общая внутренняя касательная к окружностям с радиусами R и r пересекает их общие внешние касательные в точках А и В и касается одной из окружностей в точке С. Докажите, что

Д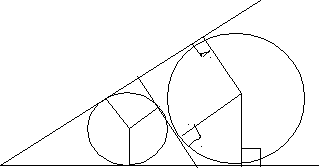оказательство.

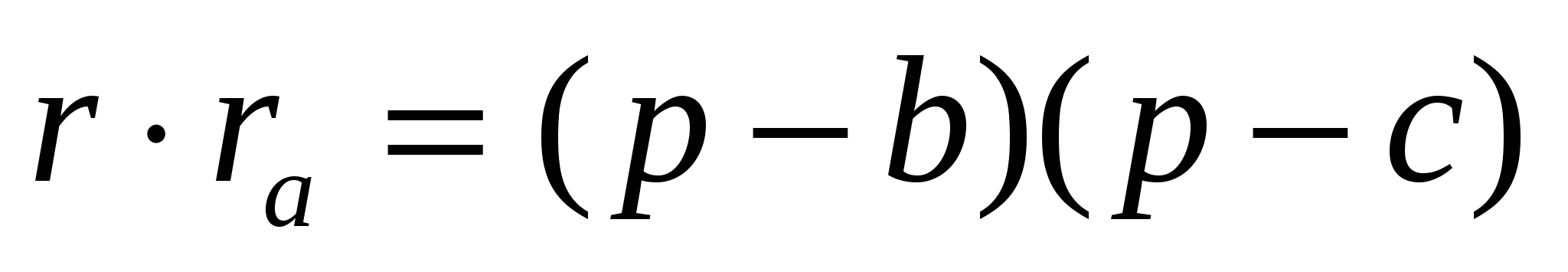
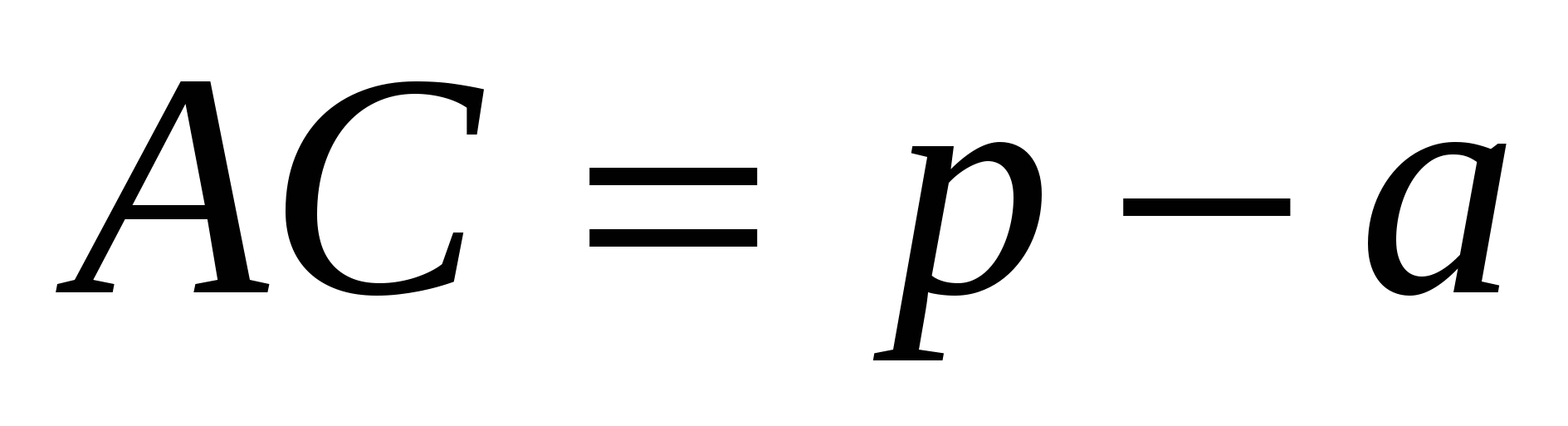
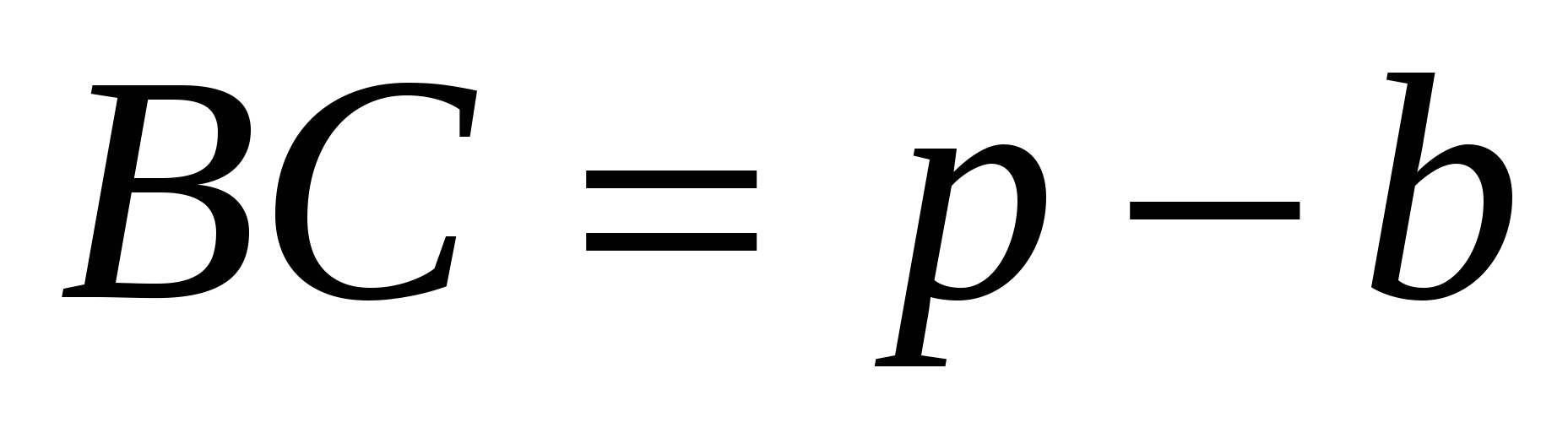
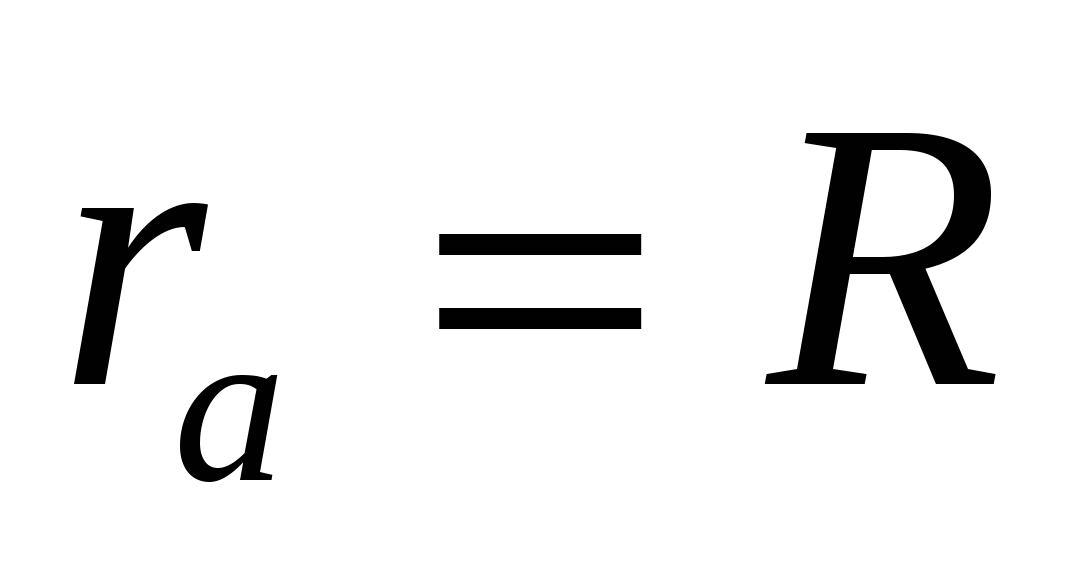
На основании сформулированного в теоретической части свойства имеем:

, . Учитывая, что получаем:

Эту же задачу можно решить, используя другие свойства вневписанной окружности.

Пусть С и D – точки касания касательной АВ с вневписанной и вписанной окружностями. Тогда АВ = ММ₁= NN ₁ (задача 2), МВ = ВС, NA = АС, DA = AN ₁.

NN₁ = NA + AN₁ = AC + AD, NN₁ = AC + AD = 2AD + CD,

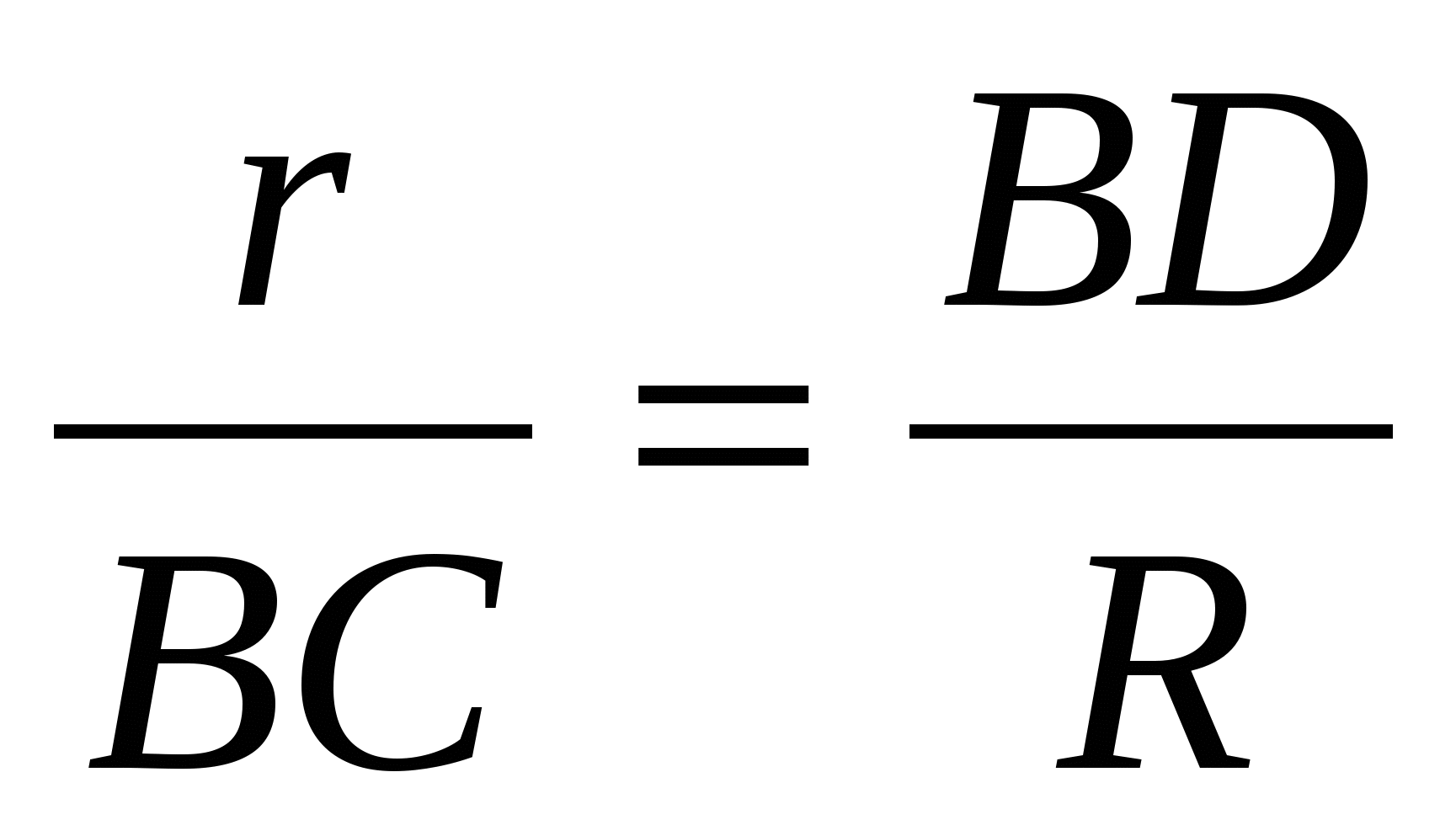
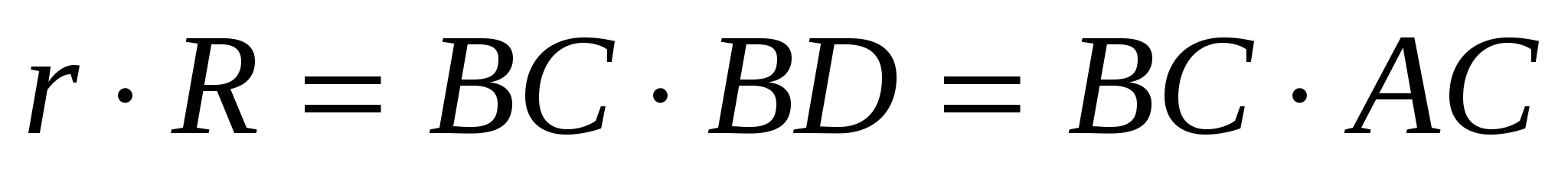
Таким образом, BD = AC. , . Что и требовалось доказать.

2. Задачи на построение

Задача 1. Построить треугольник по периметру и двум углам.

Дано: углы  и  , периметр треугольника P

1. Построить отрезок, равный полупериметру (АК).

2. Из точки А построить данный по условию угол  , а из точки К восстановить перпендикуляр.

3. Построить биссектрису угла САВ.

4. Построить окружность с центром в точке пересечения биссектрисы угла А с перпендикуляром О_аК и радиусом О_аК.

5. На отрезке АК построить второй данный угол  так, чтобы его луч был касательной к окружности.

6. Данная касательная пересечет вторую сторону угла в точке В.

— искомый треугольник.

Задача 2. Постройте треугольник, если дана сторона, противолежащий ей угол треугольника и сумма двух других сторон.

Решение. Пусть дана сторона а, угол А и сумма сторон b + c . Тогда известна длина

полупериметра искомого треугольника. Значит, известны положения точек T ₁ и T ₂ на сторонах угла А. Восстановив перпендикуляры в этих точках к сторонам угла А, на их пересечении получим центр вневписанной окружности, а значит, вневписанная окружность построена.

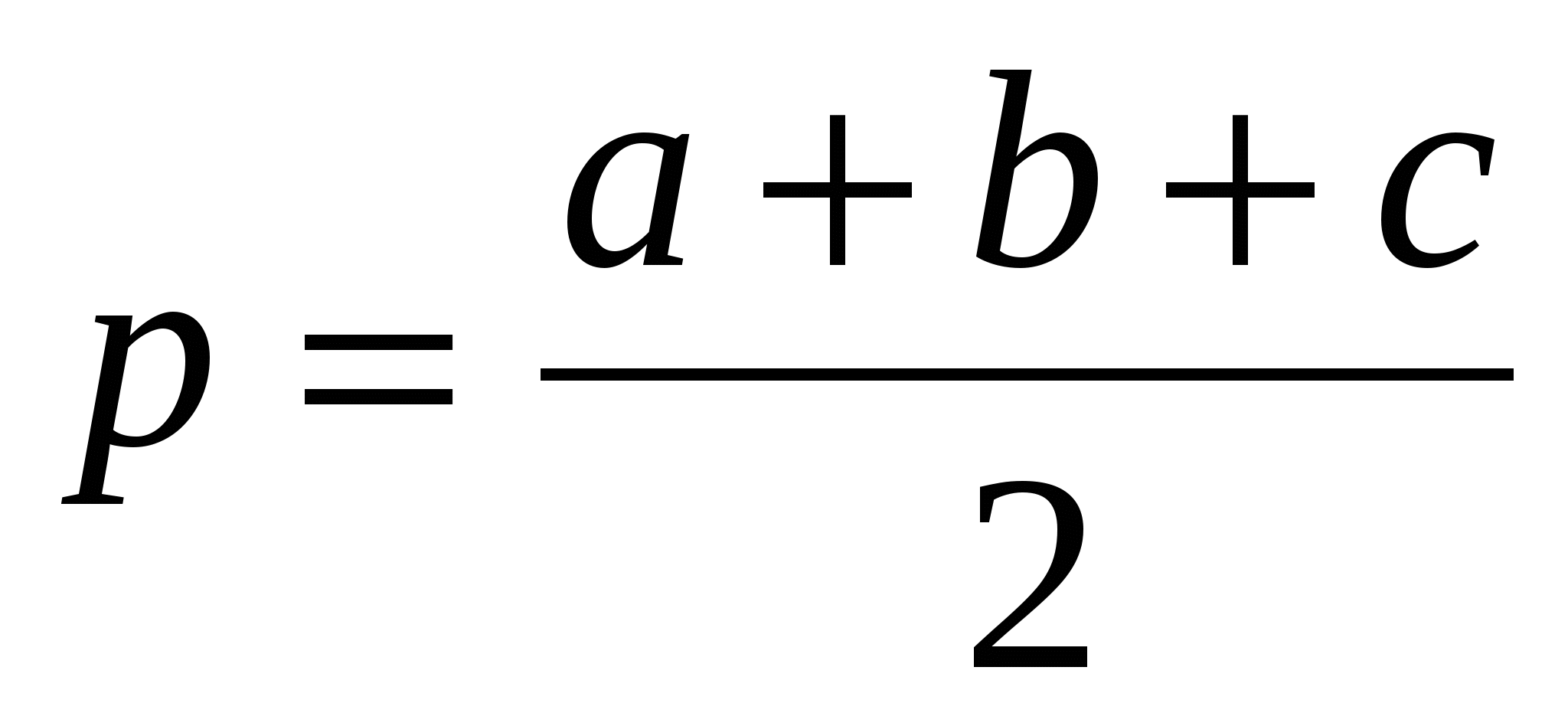
Расстояние от точки Т₁ до точки касания вписанной окружности равно а. Следовательно, мы можем найти точки касания вписанной окружности искомого треугольника со сторонами угла А и построить саму вписанную окружность. Общая внутренняя касательная к построенным окружностям отсекает на сторонах угла искомый треугольник.

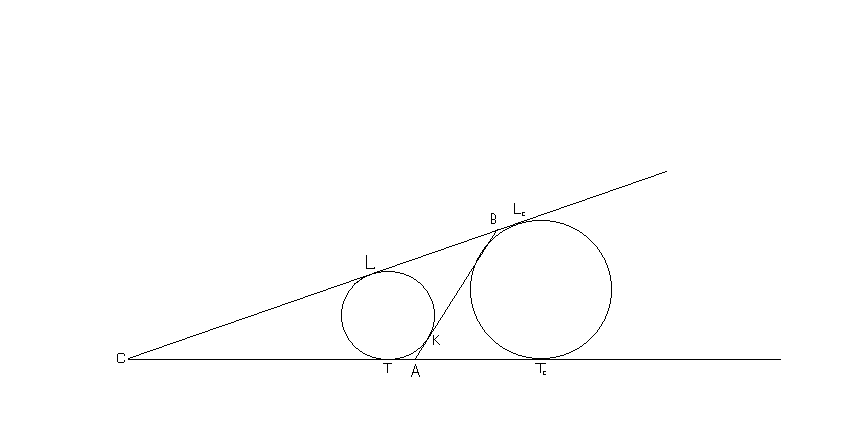
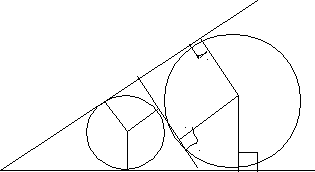
Задача 3. Построить треугольник ABC , если известна сторона AB , радиус r вписанной окружности и радиус r _c вневписанной окружности, касающейся стороны АВ и продолжений сторон АС и ВС. Рис.3.

Предположим, что искомый треугольник построен. Отметим точки касания Т и Т_с с прямой АС вписанной и вневписанной окружностей (радиусов r и r _c соответственно). Воспользуемся тем, что отрезки АВ и T Т_с равны по длине. Отсюда вытекает способ построения: отмечаем на прямой две точки Т и Т_с на расстоянии АВ, строим по одну сторону этой прямой окружности радиусов r и r _c , касающиеся ее в точках Т и Т_с, проводим еще одну внешнюю и одну внутреннюю общую касательную к этим окружностям – и нужный треугольник построен. Задача имеет решение в том и только в том случае, если .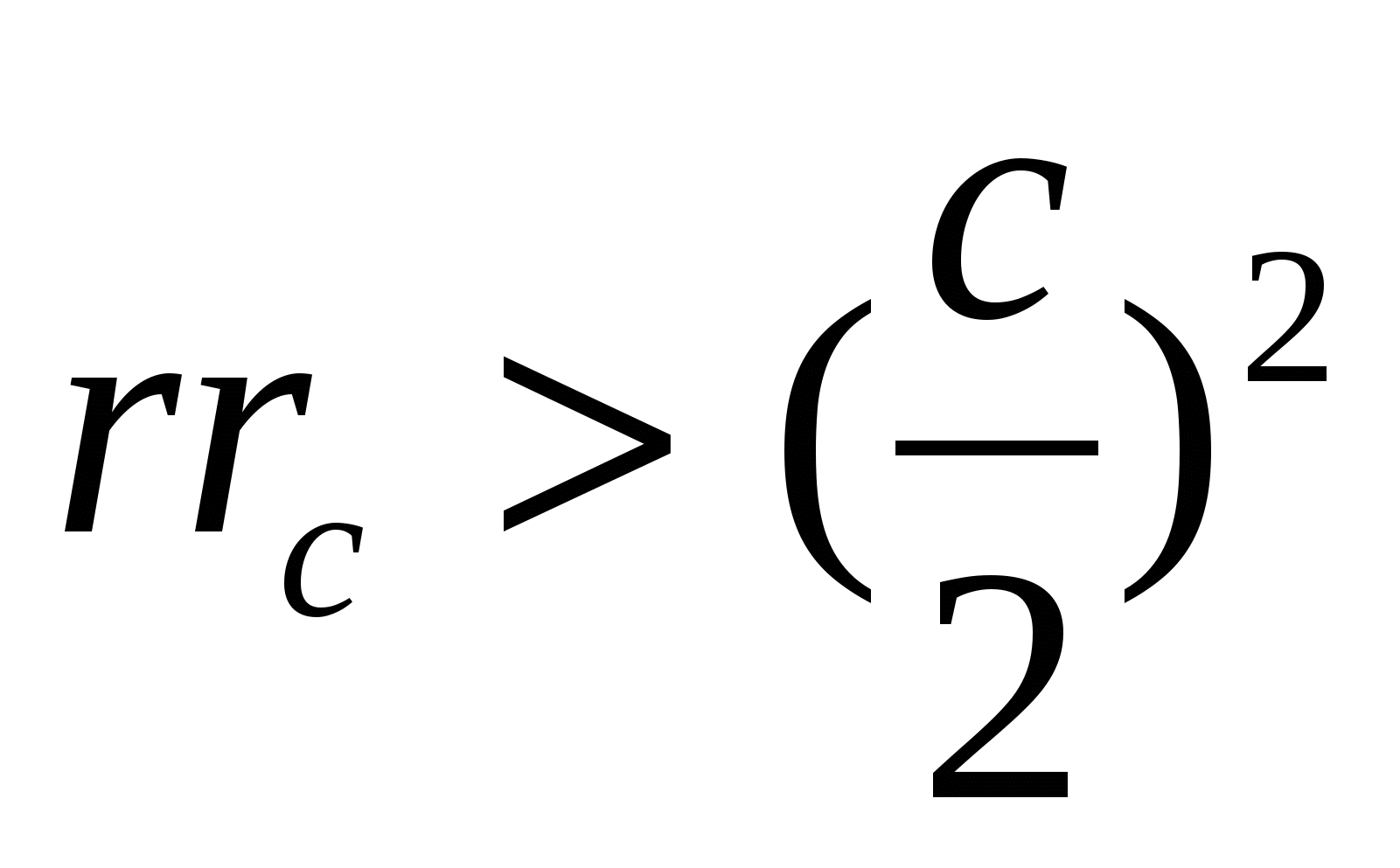

Задача 4. Дан угол К, меньший развернутого, и точка Р, расположенная внутри угла, смежного с данным. Провести через точку Р прямую, отсекающую от угла К треугольник заданного периметра.

Решение. Решение основано на применении теоремы, которая, казалось бы, очень далека от ситуации, описываемой в условии задачи, — теоремы о двух касательных, проведенных к окружности из одной точки.

П

усть l – какая-либо проходящая через Р прямая. М и N – точки ее пересечения со сторонами угла. Проведем вневписанную окружность треугольника MKN. AM = ME и EN = NB, где А и В – точки касания окружности со сторонами угла. Тогда периметр отсекаемого треугольника равен .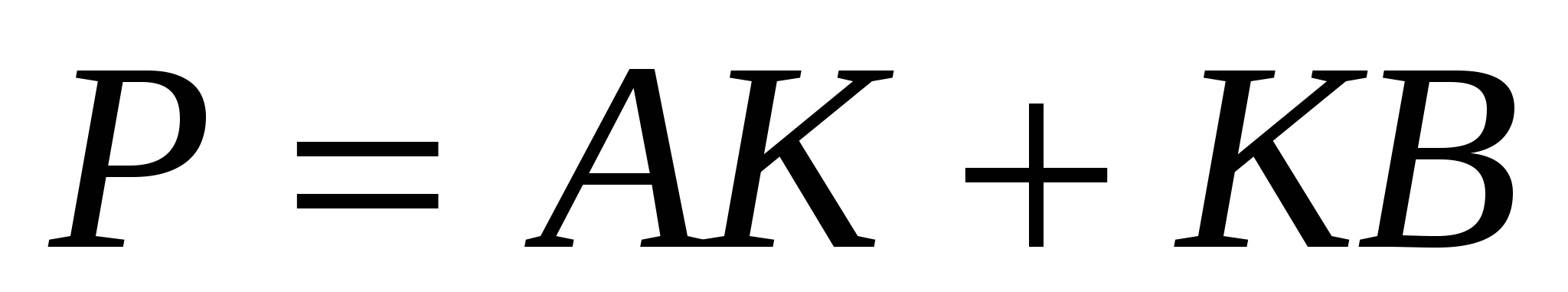

1. Построить отрезки касательных .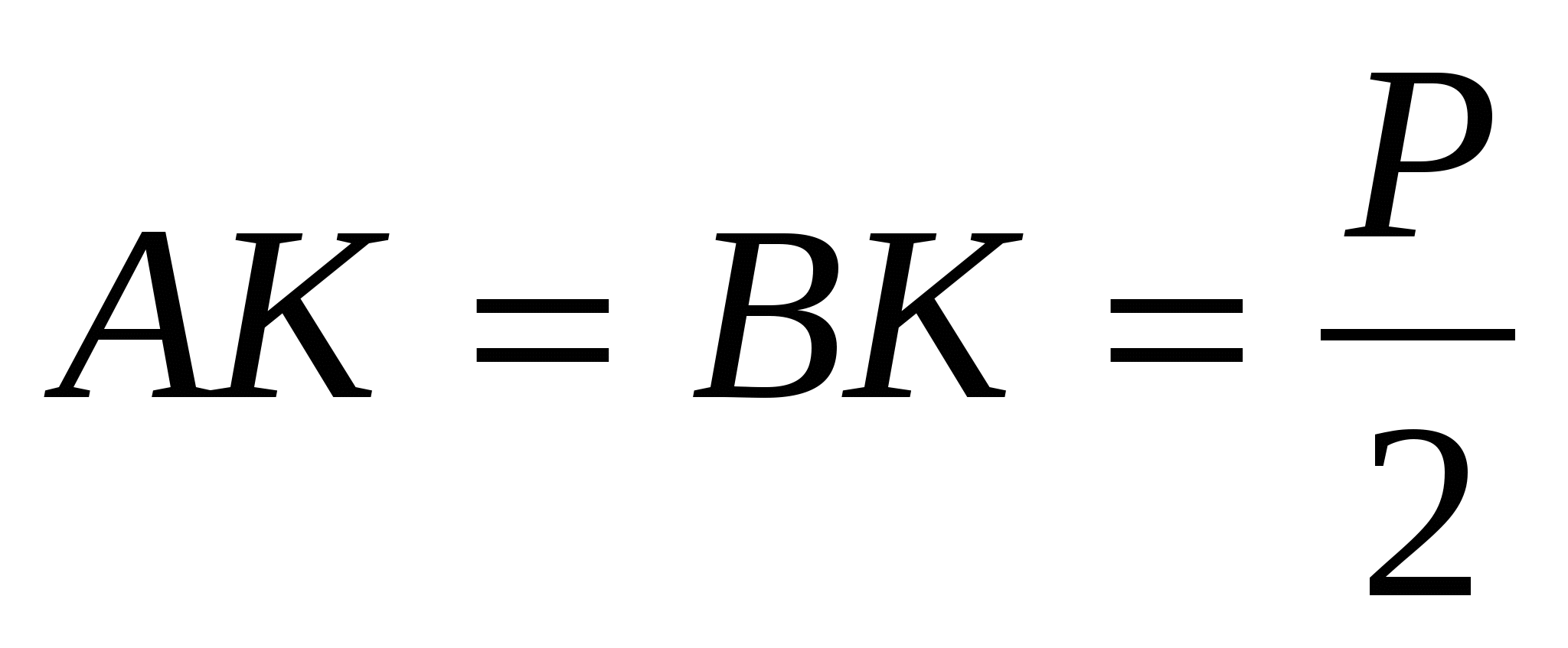

2. Восстановить из точек А и В перпендикуляры, найти их точку пересечения О_а.

4. Построить из точки Р касательную к окружности.

3. Решение стереометрических задач

При решении задач, связанных с пирамидой, полезными являются следующие утверждения.

Утверждение 1. Следующие три предложения равносильны:

а) ортогональная проекция вершины пирамиды на плоскость основания является центром вписанной окружности в многоугольник, лежащий в основании;

б) высоты боковых граней – треугольников, проведенные из вершины пирамиды, равны и лежат на соответствующих боковых гранях;

в) двугранные углы при основании пирамиды равны.

Утверждение 2. Следующие три предложения равносильны:

а) ортогональная проекция вершины пирамиды на плоскость основания равноудалена от прямых, содержащих стороны основания пирамиды;

б) высоты боковых граней – треугольников, проведенные из вершины пирамиды, равны;

в) плоскости боковых граней образуют равные углы с плоскостью основания.

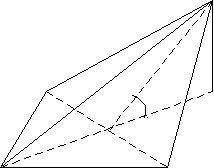
Задача 1. В основании пирамиды, все плоскости боковых граней которого наклонены к плоскости основания под углом  , лежит правильный треугольник со стороной а. Найти объем пирамиды.

Решение. Следует отметить, что неопределенность решения возникает в связи с различным положением ортогональной плоскости. Пусть SABC – данная пирамида, О – ортогональная проекция вершины S на плоскость основания АВС. Согласно утверждению 3, точка О равноудалена от прямых АВ, АС и ВС. Не ограничивая общности рассуждений, имеем два случая расположения точки О:

Вершина тетраэдра проектируется в центр вписанной окружности.

Рис .1. S

, , ,

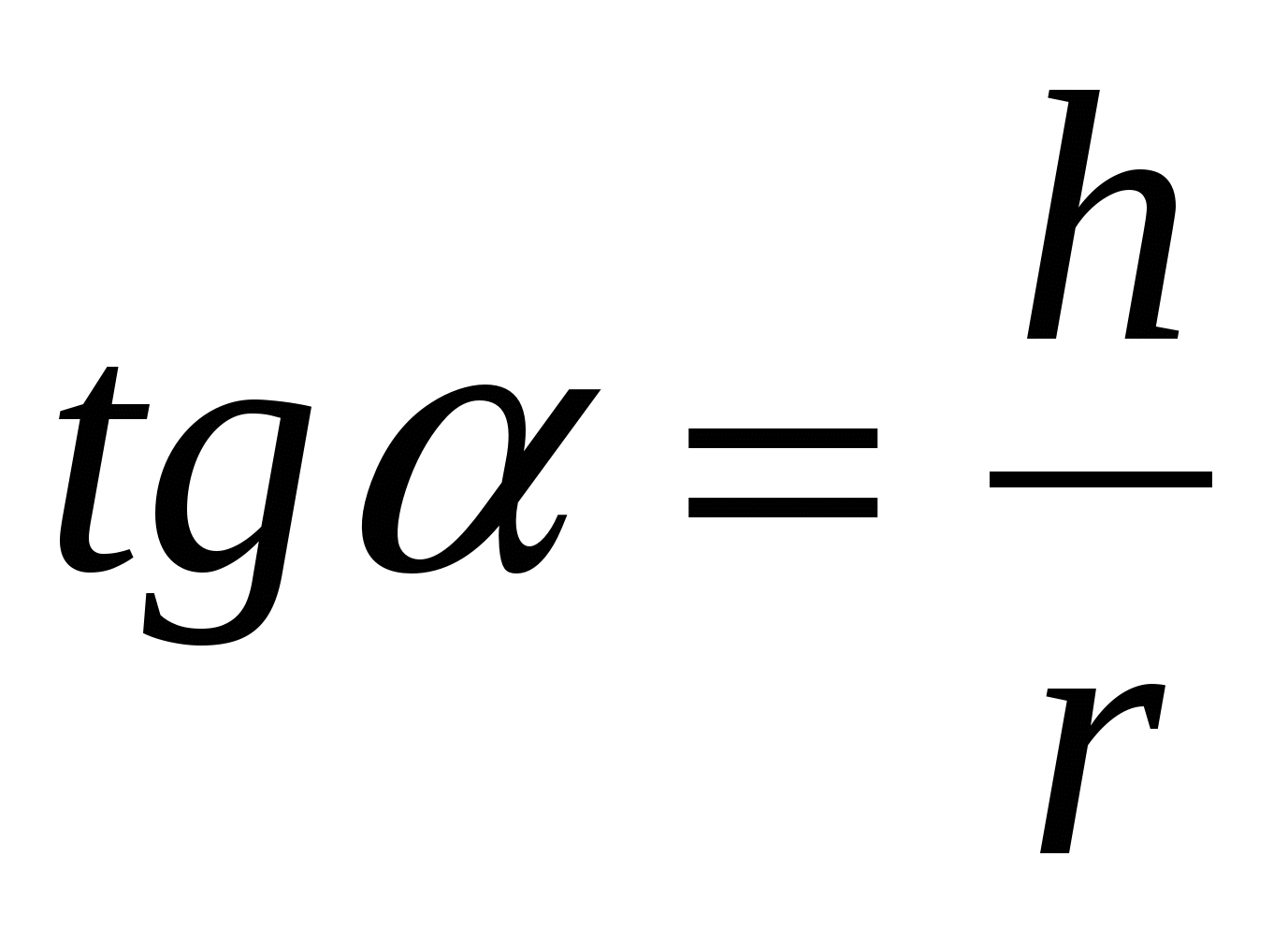
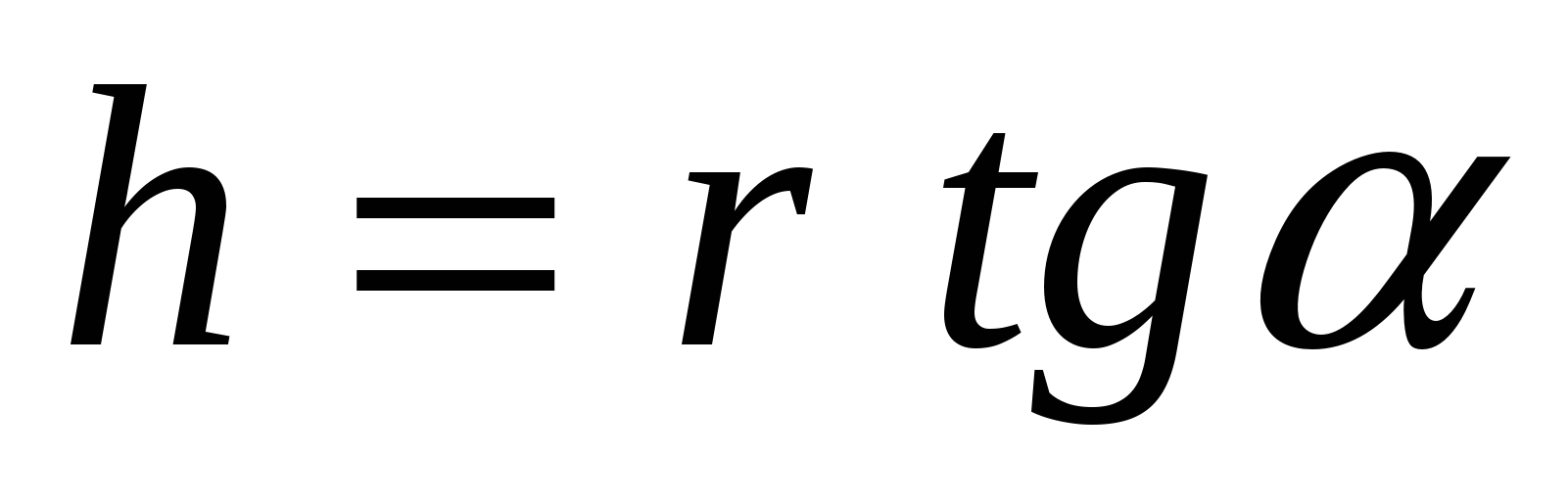
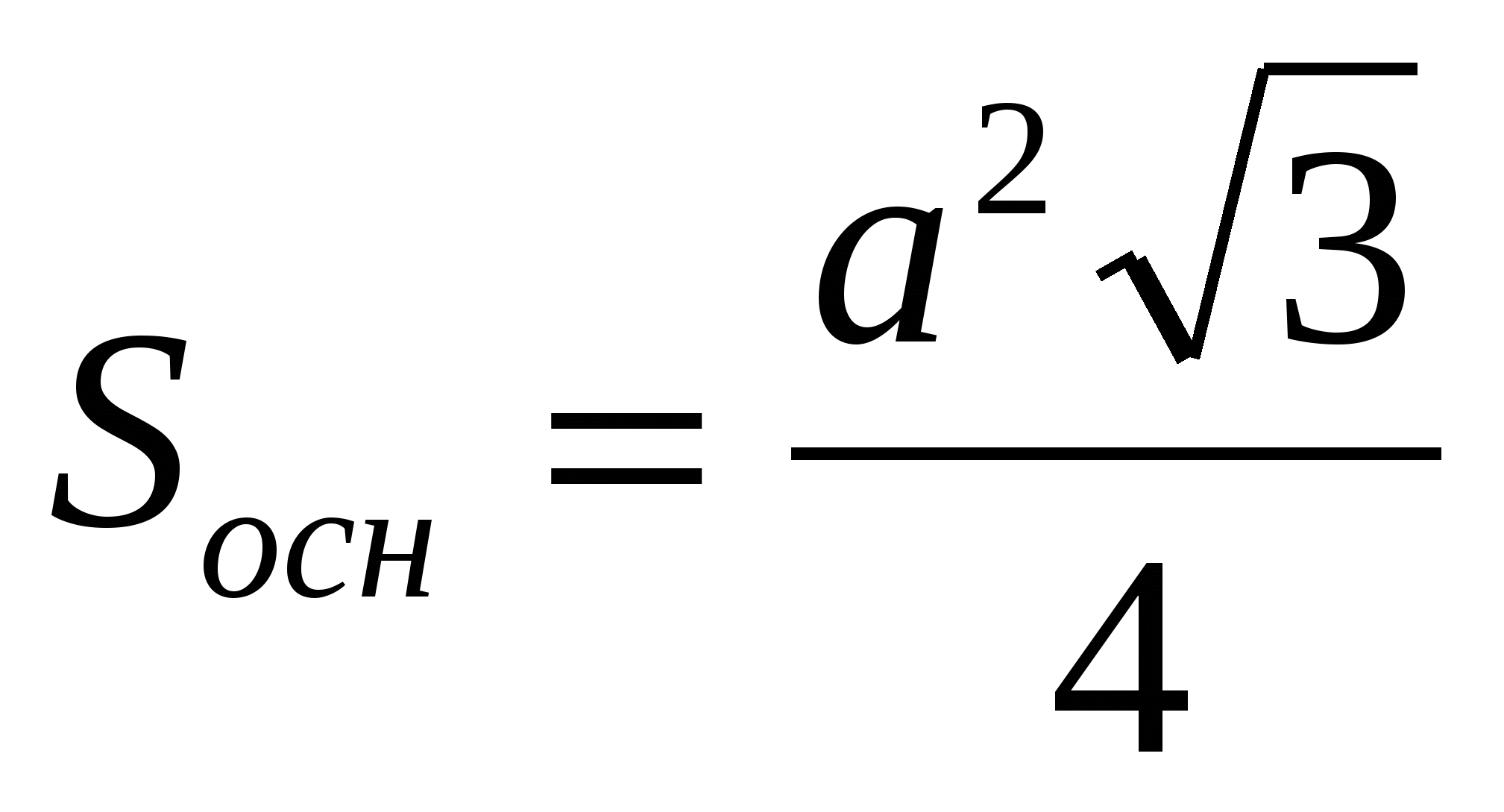
h B ,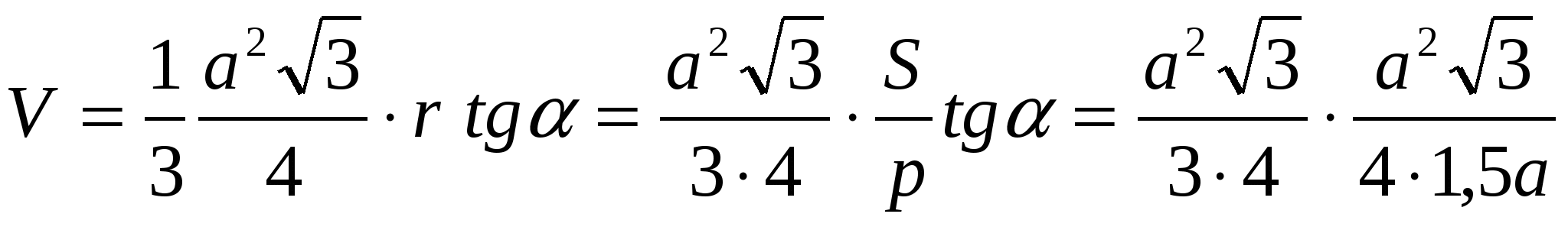

A О  M .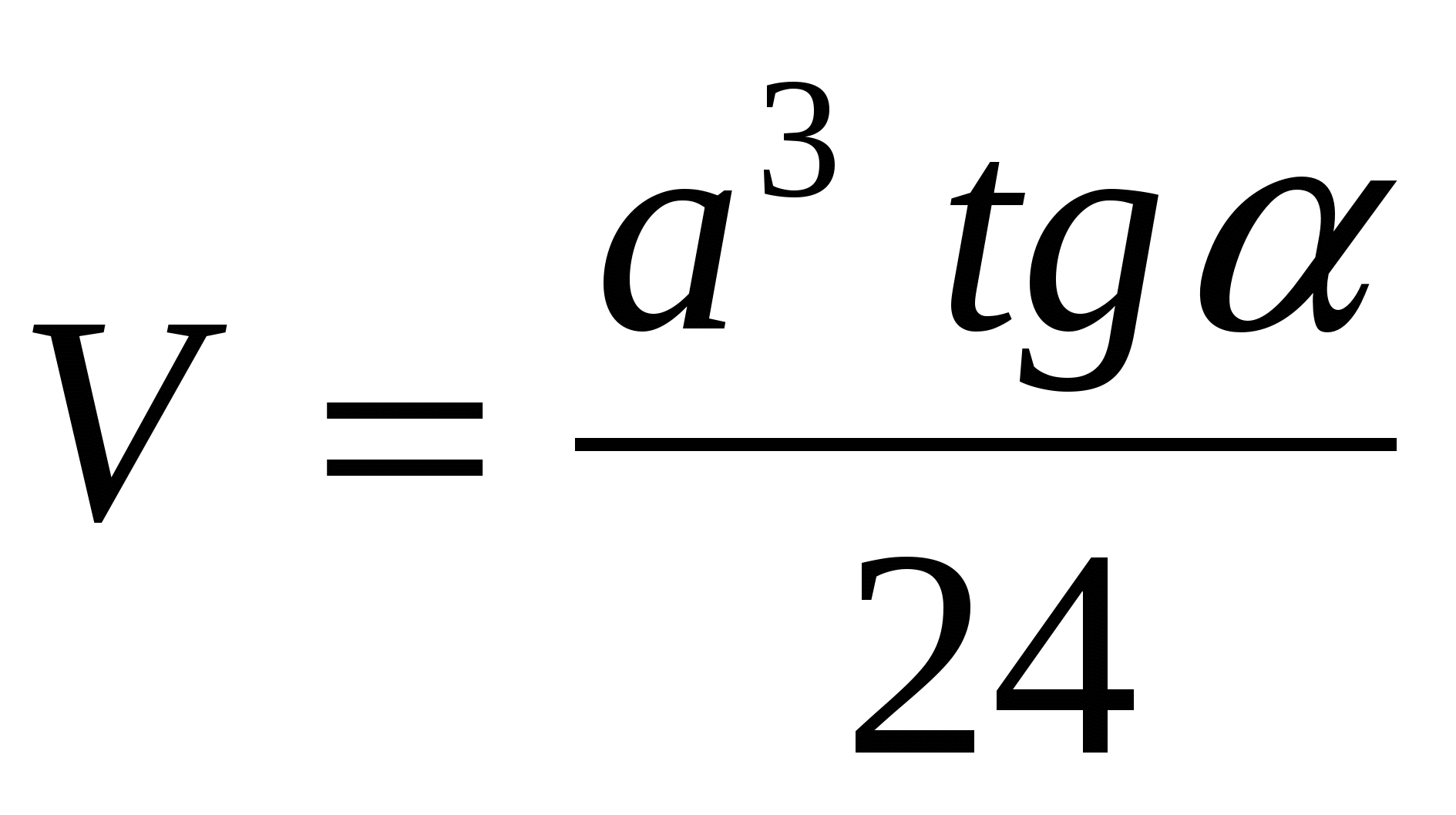

Вершина тетраэдра проектируется в центр вневписанной окружности.

S А

, , ,

.

.

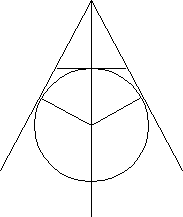
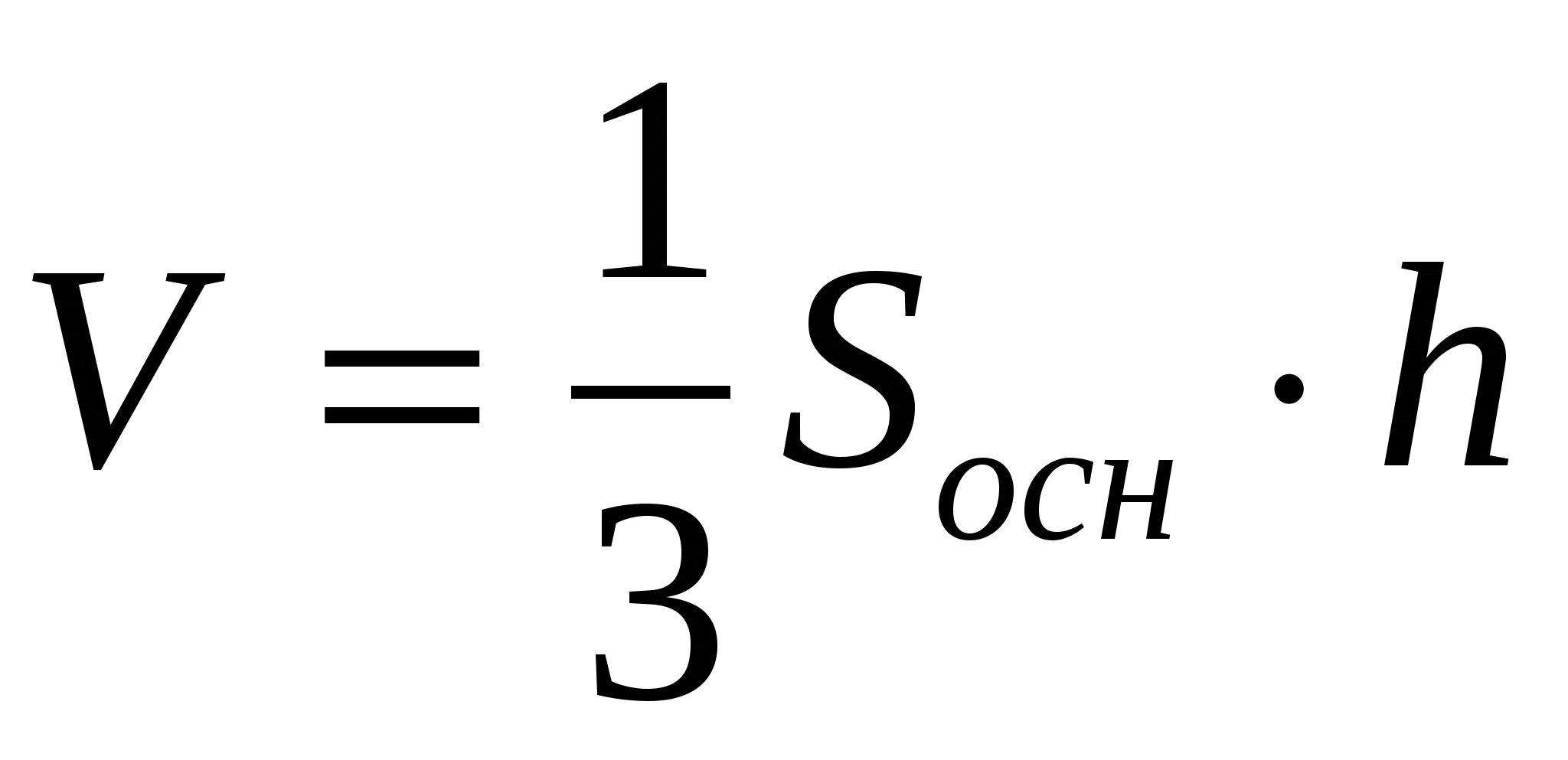
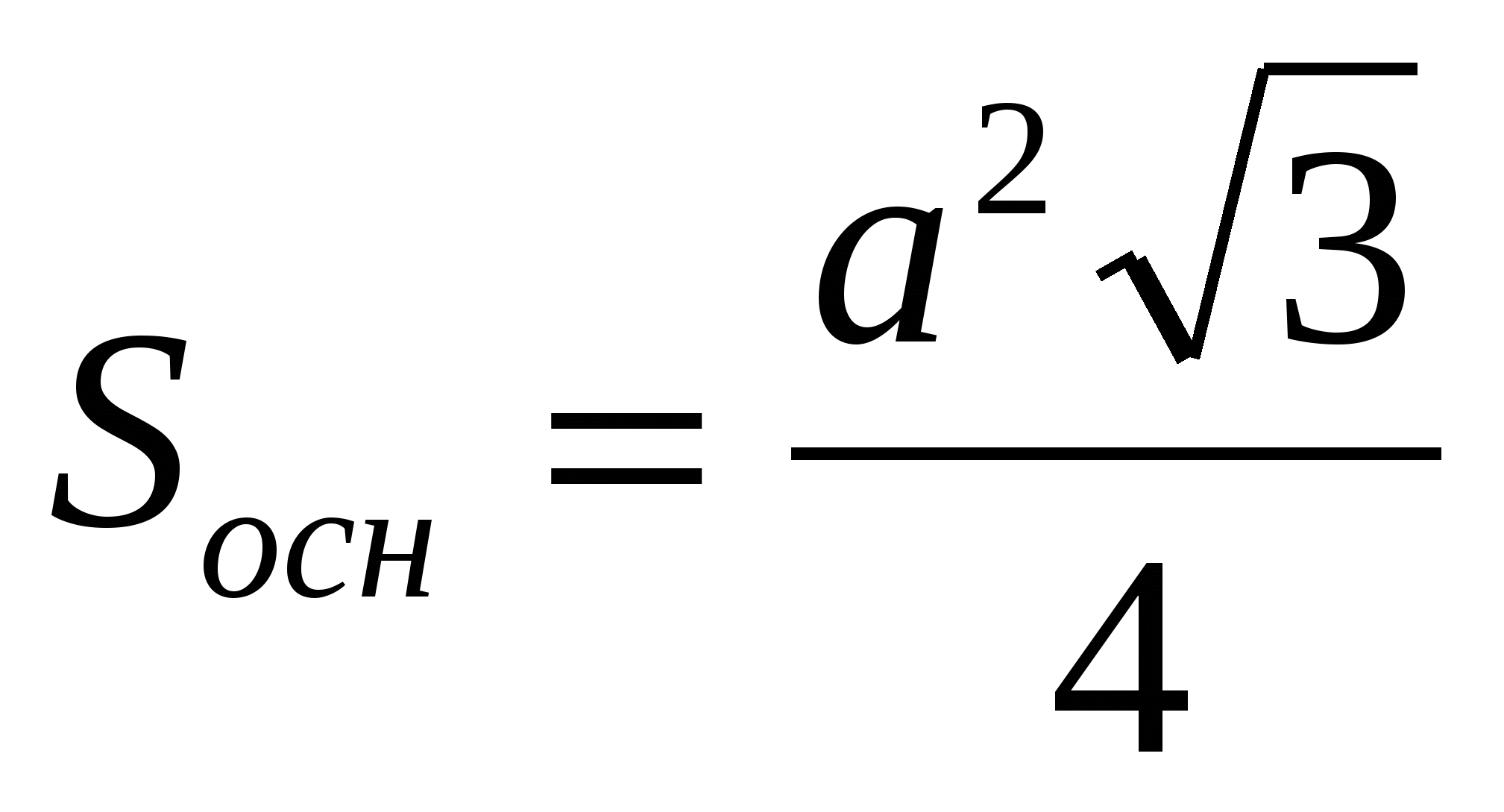
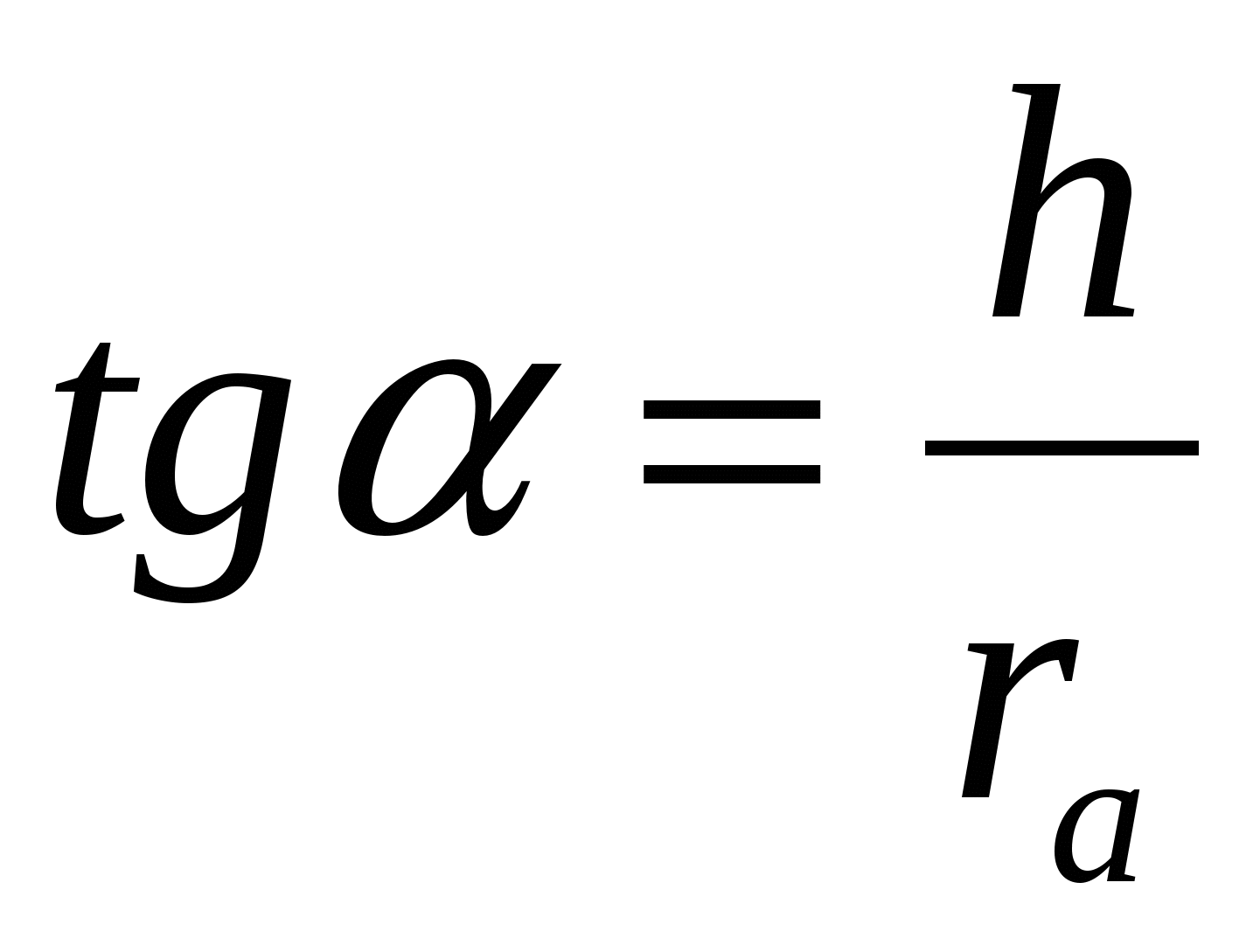
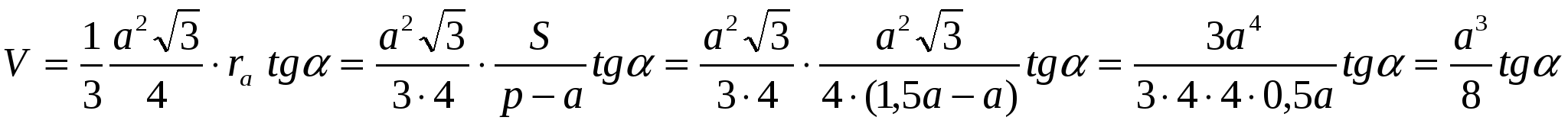
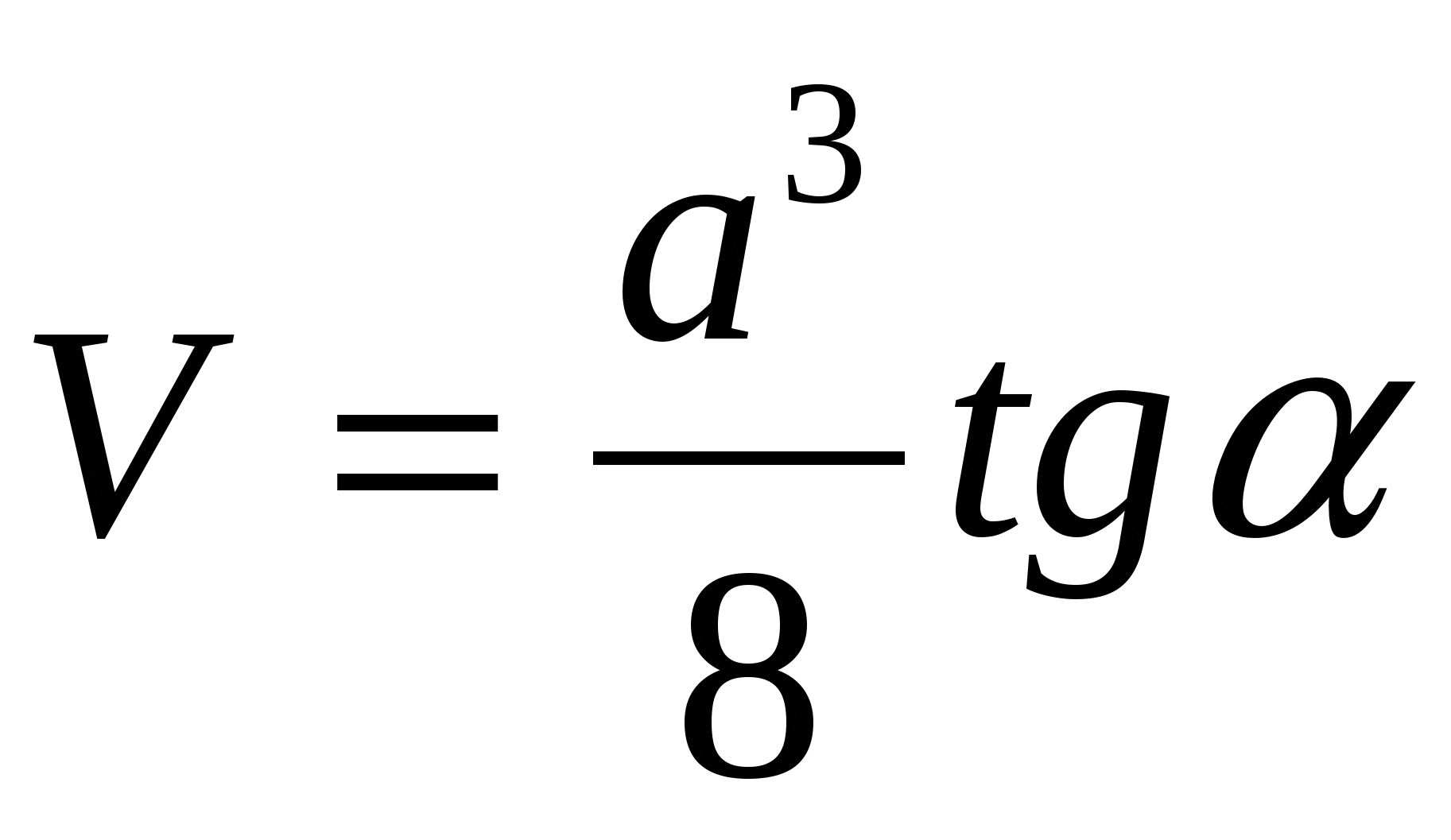
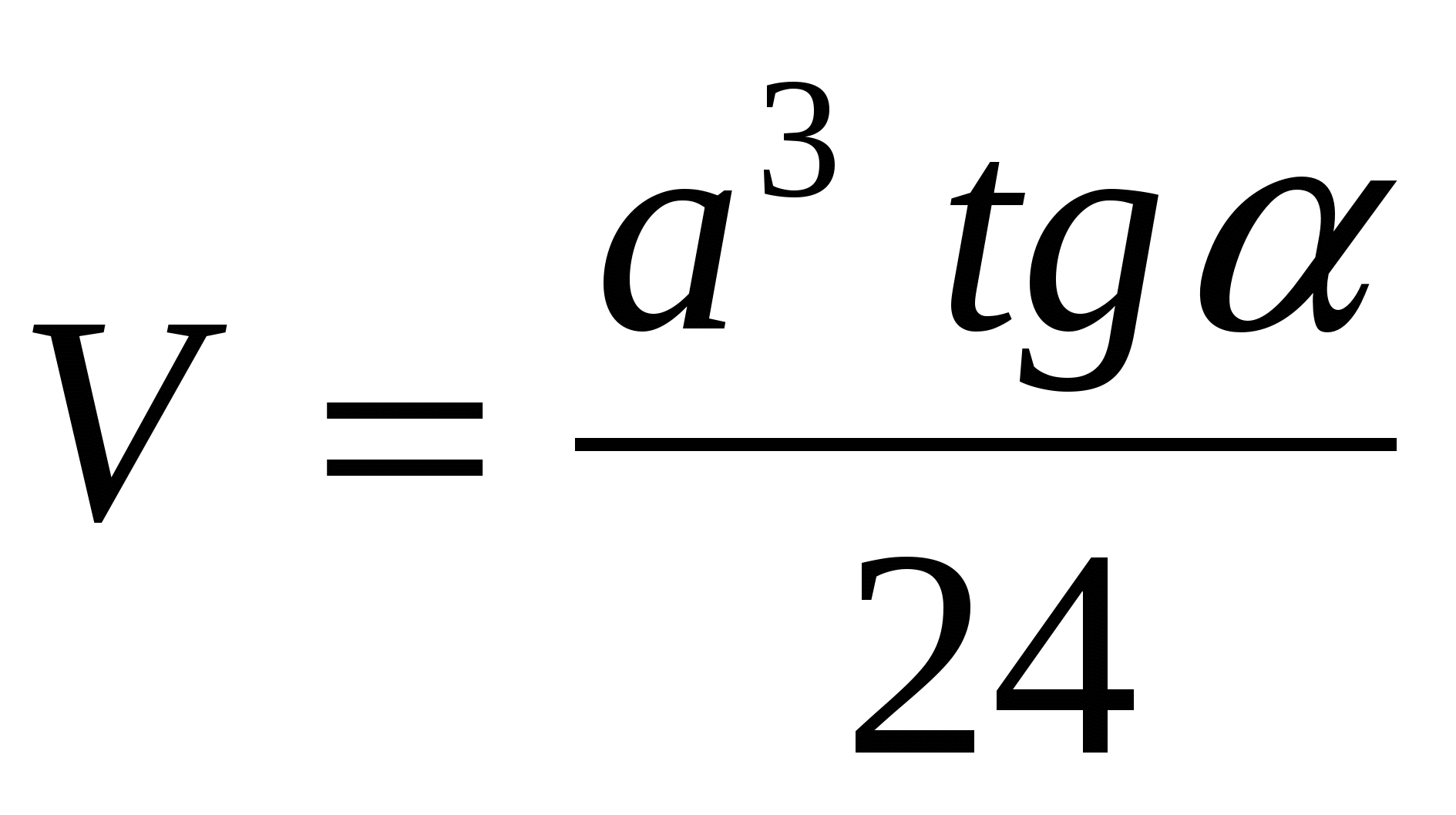
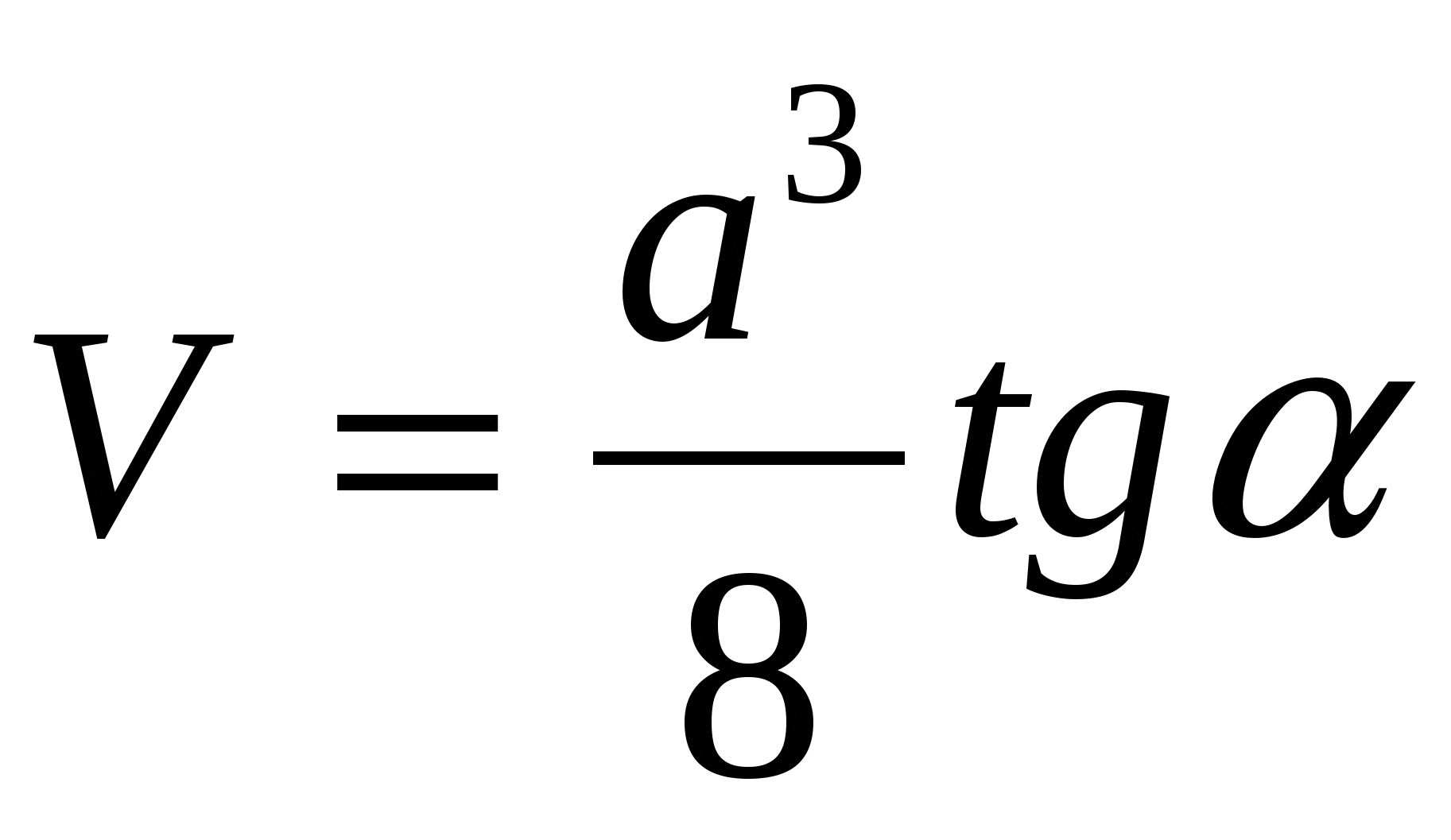
Ответ: 1) ; 2) .

Задача 2. Следует отметить, что если решать задачу в привычной формулировке, используемой в школьном учебнике: «Длины сторон основания треугольной пирамиды равны a, b и c. Боковые грани с основанием пирамиды составляют угол  . Вычислить объем пирамиды», то задача будет иметь только одно решение: на основании утверждения 1. вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды.

«Длины сторон основания треугольной пирамиды равны a, b и c. Плоскости боковых граней с плоскостью основания пирамиды составляют угол  . Вычислить объем пирамиды»

В такой формулировке условию задачи соответствуют четыре пирамиды, имеющие общее основание и отличающиеся только высотами: , , , .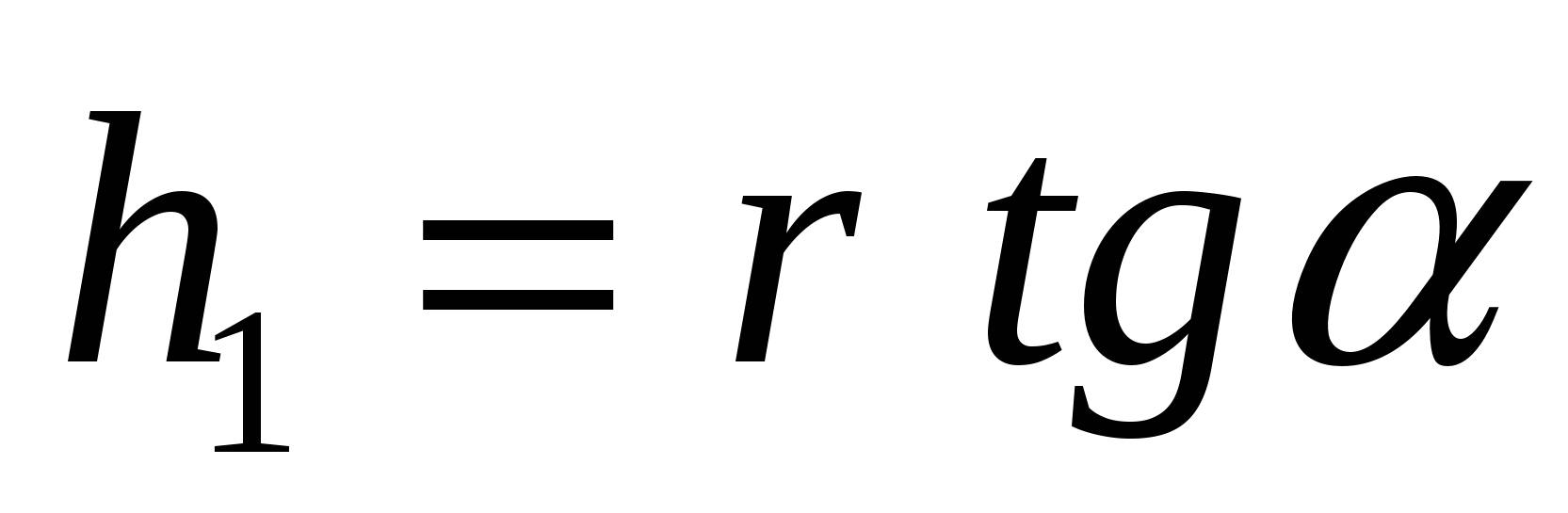

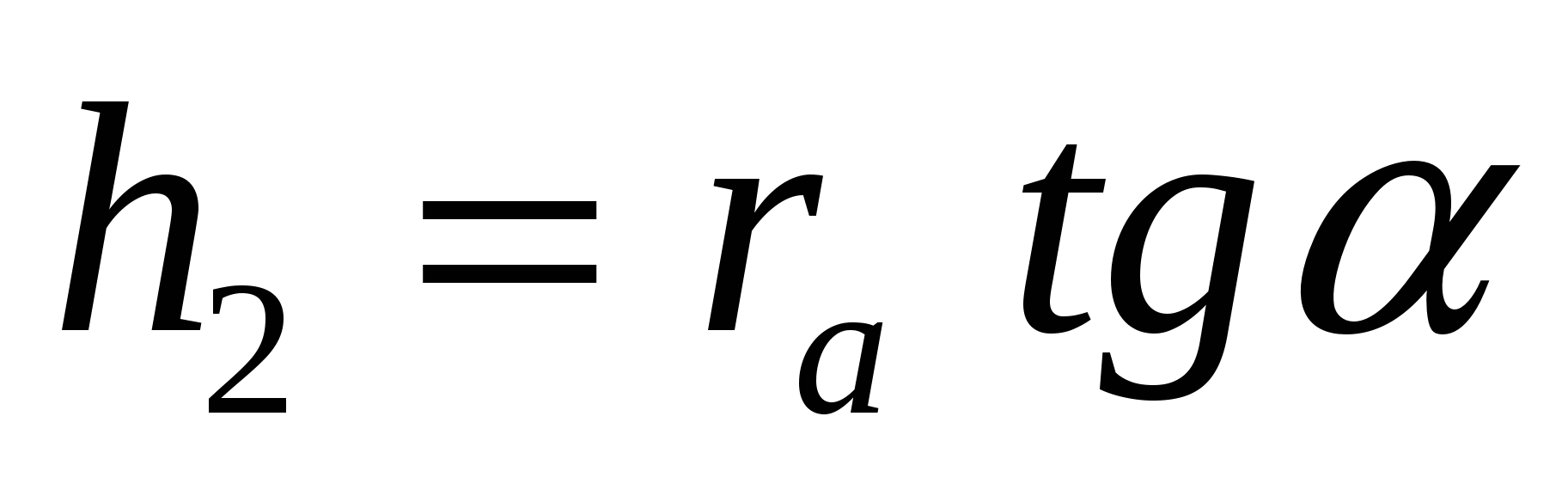
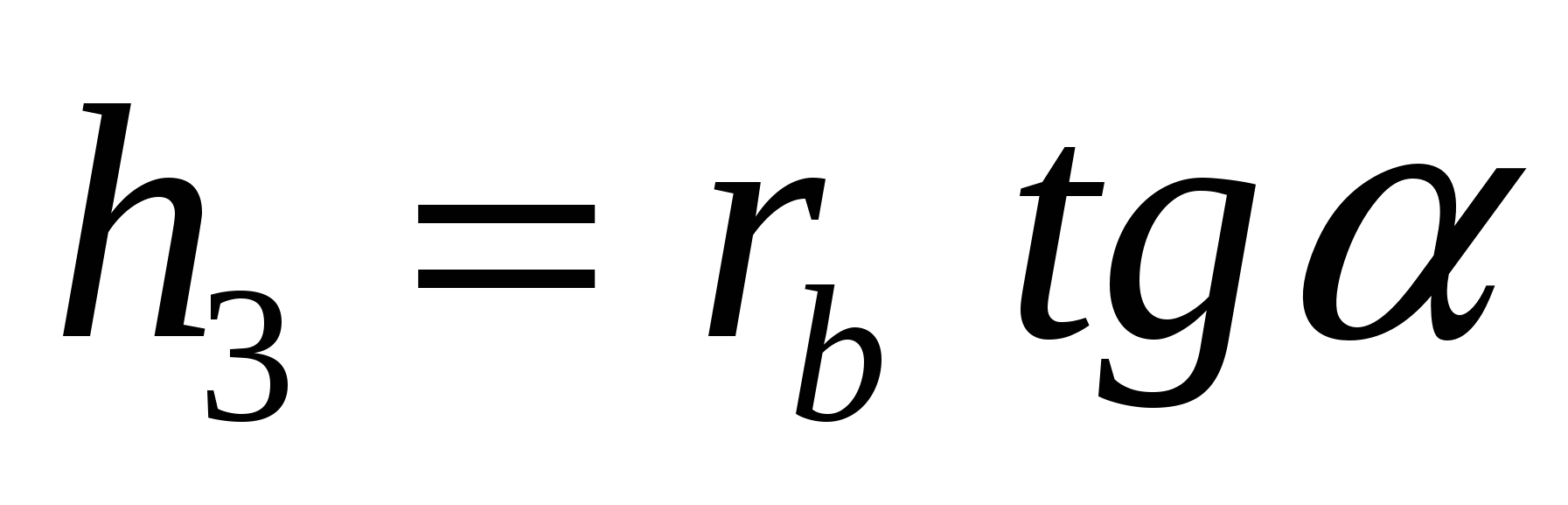
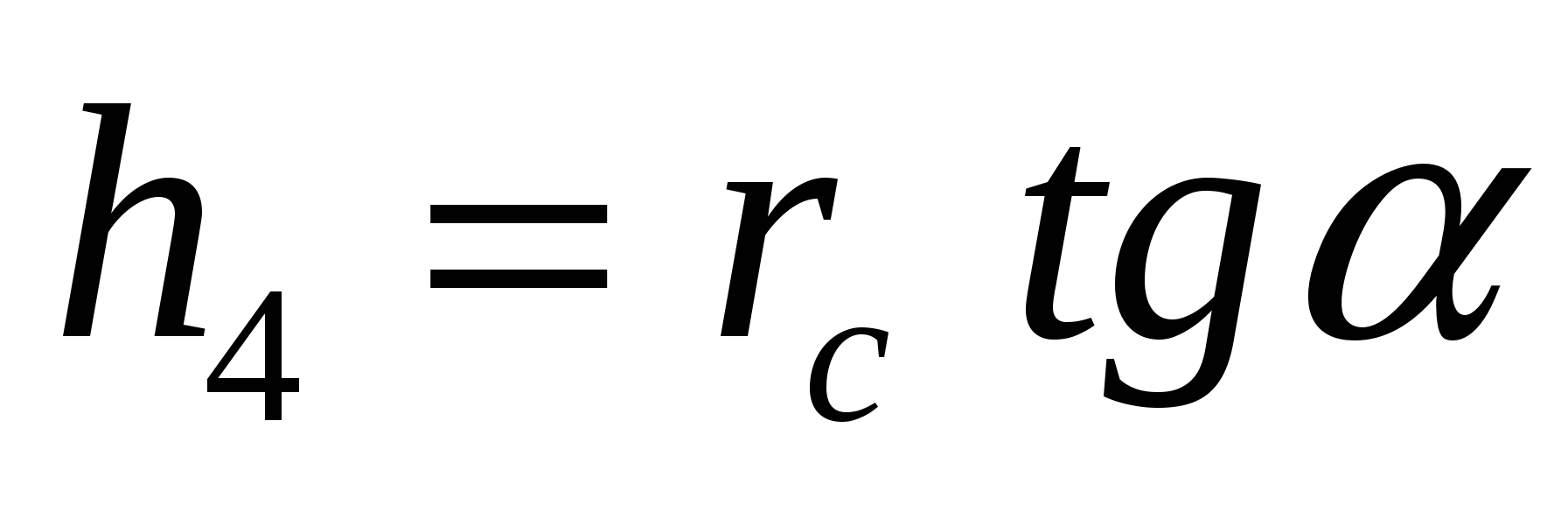
После преобразований получаем , , , .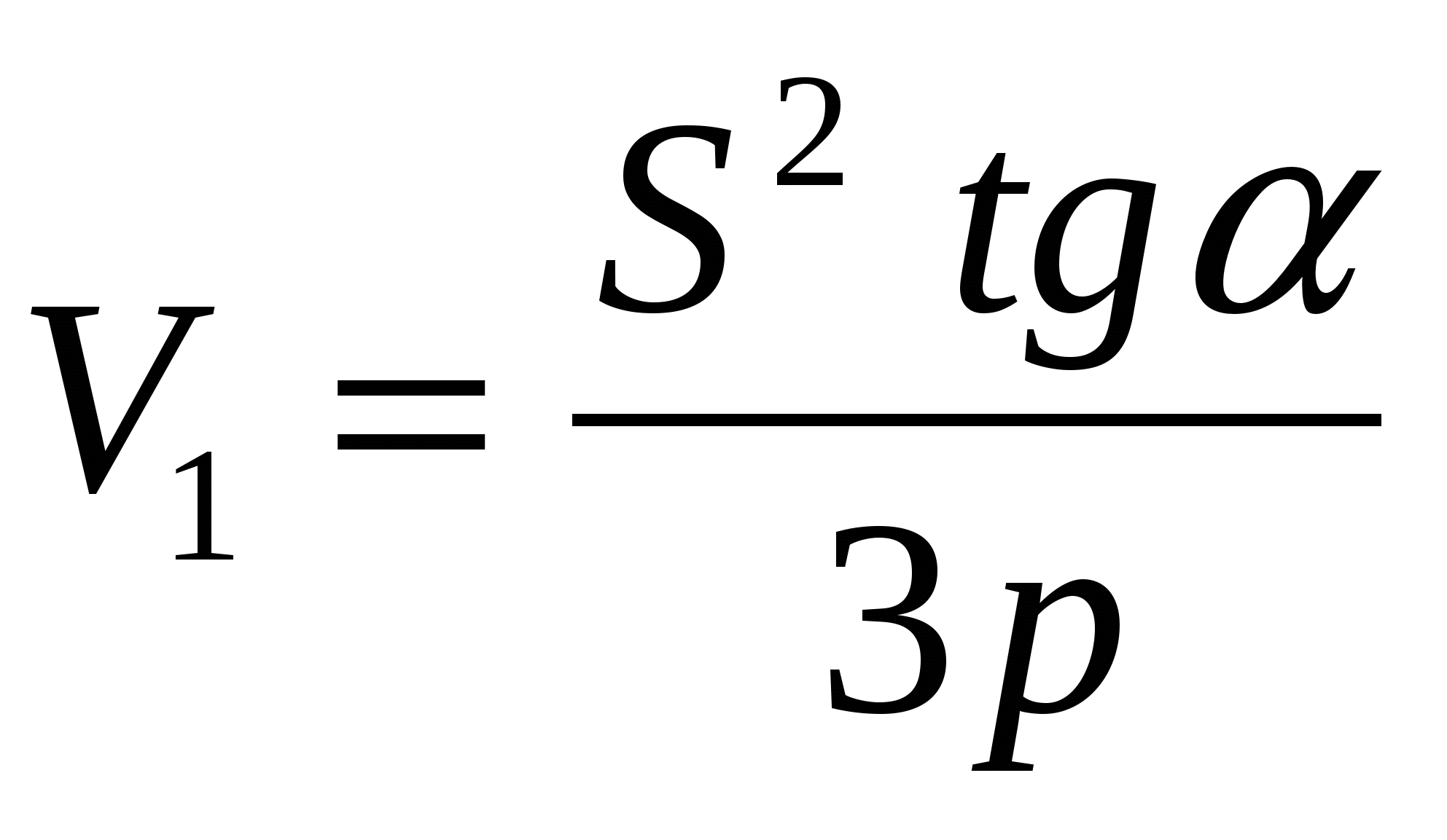

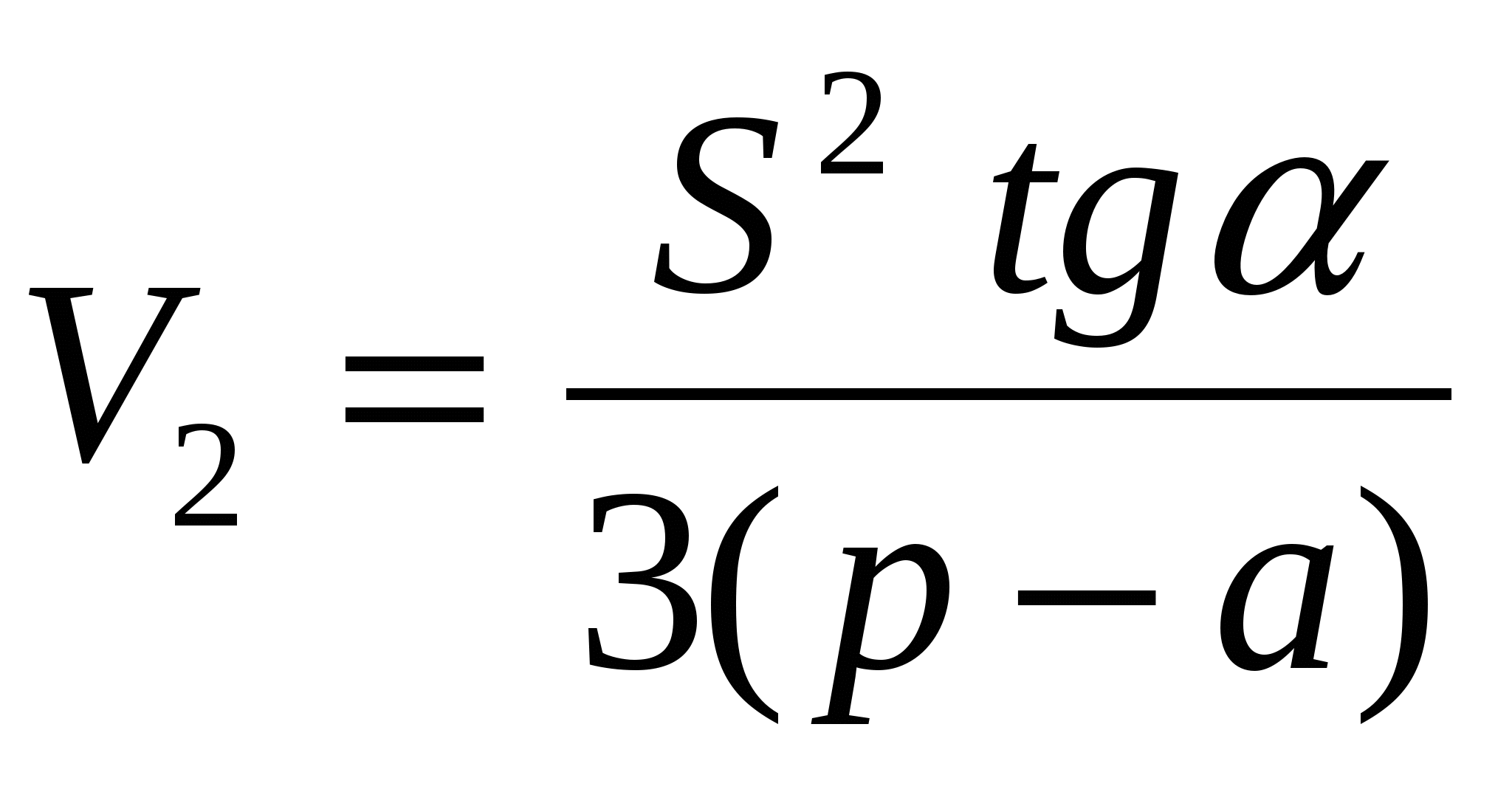
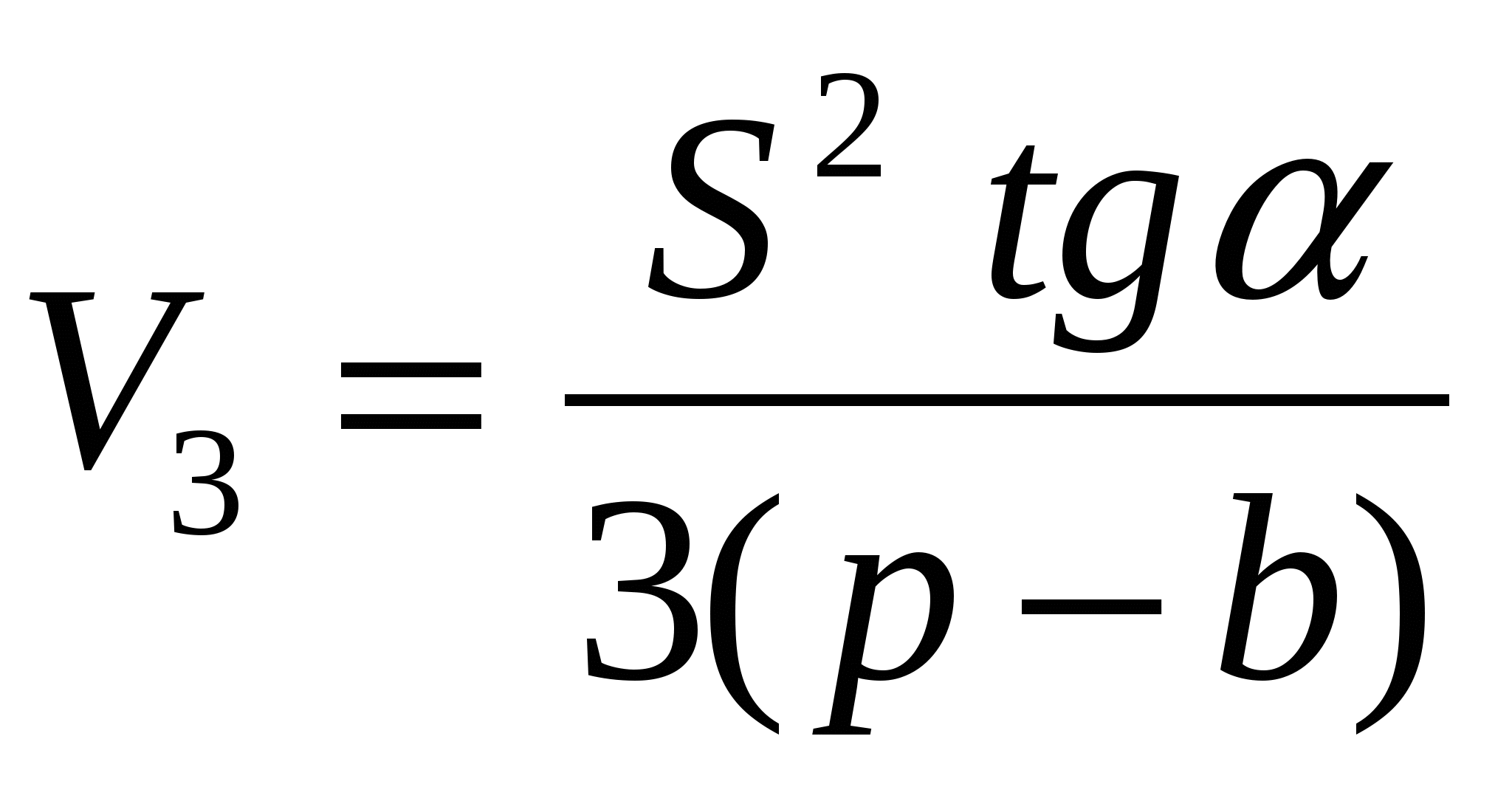
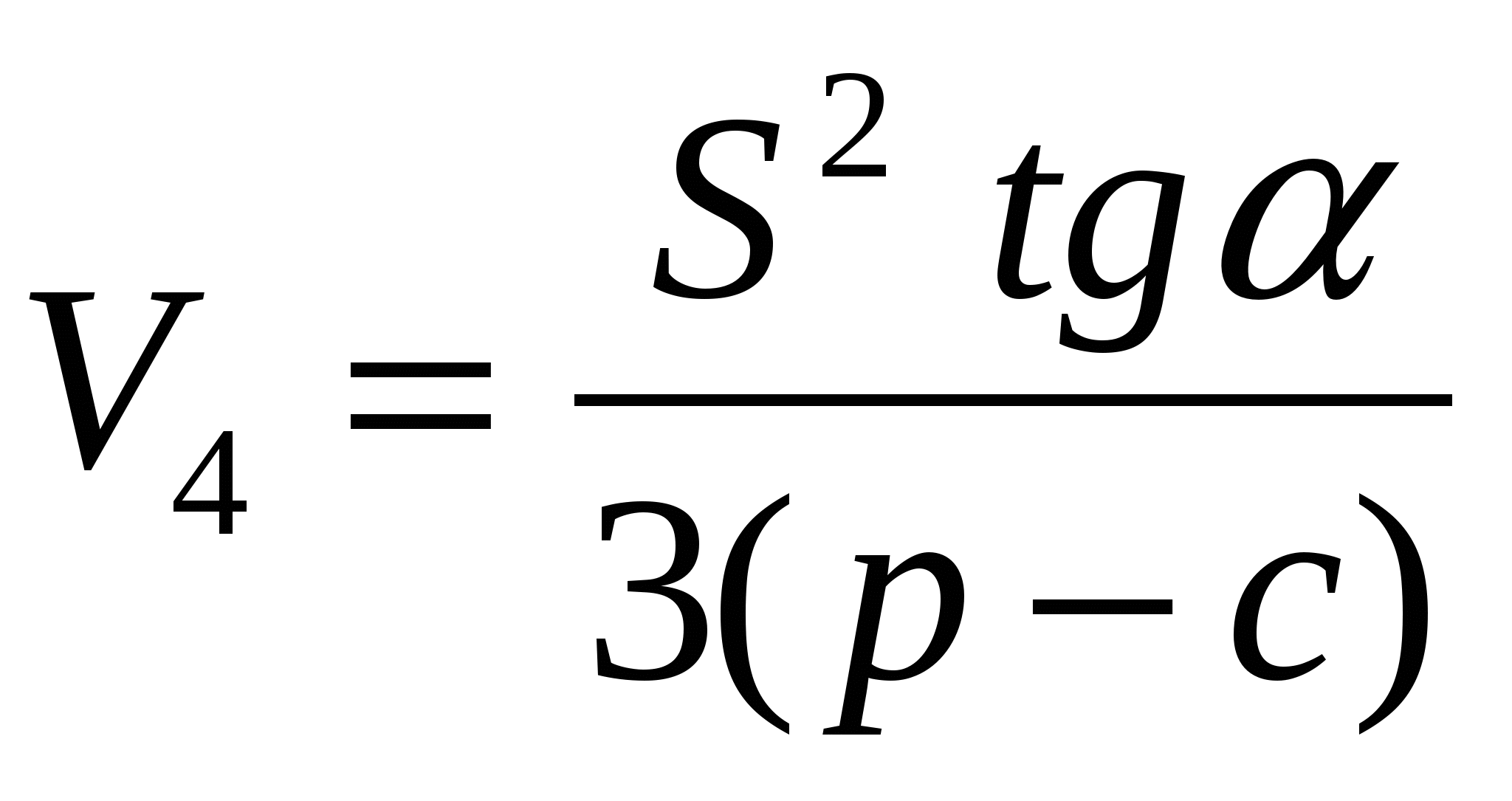
Очевидно, что, если треугольник, лежащий в основании пирамиды разносторонний, имеем четыре различных значения искомого объема пирамиды, если треугольник равнобедренный – три, правильный – два.

Процесс решения таких задач вполне доступен, если предварительно познакомиться с понятием вневписанной окружности.

В заключение мы еще раз хотим сказать, что геометрия начинается с треугольника. Треугольник неисчерпаем. Две с половиной тысячи лет постоянно открываются его новые свойства. Чтобы рассказать обо всех известных, необходим том, сравнимый по объему с томом Большой энциклопедии.

А изящество и красота применения окружности создают ощущение ее элитарности. К сожалению, в школьной программе этой фигуре уделяется незначительное время и внимание. А про вневписанную окружность и не упоминается.

В своей работе мы проиллюстрировали связь вневписанной окружности с основными элементами треугольника и показали применение этих свойств к решению задач различного типа.

На наш взгляд данная работа может быть использована на уроках геометрии в 8-11 классах, на занятиях математического кружка, факультативах и при решении конкурсных задач.

Задания для самостоятельной работы

1.

2.

3.

4. , где — угол А треугольника АВС

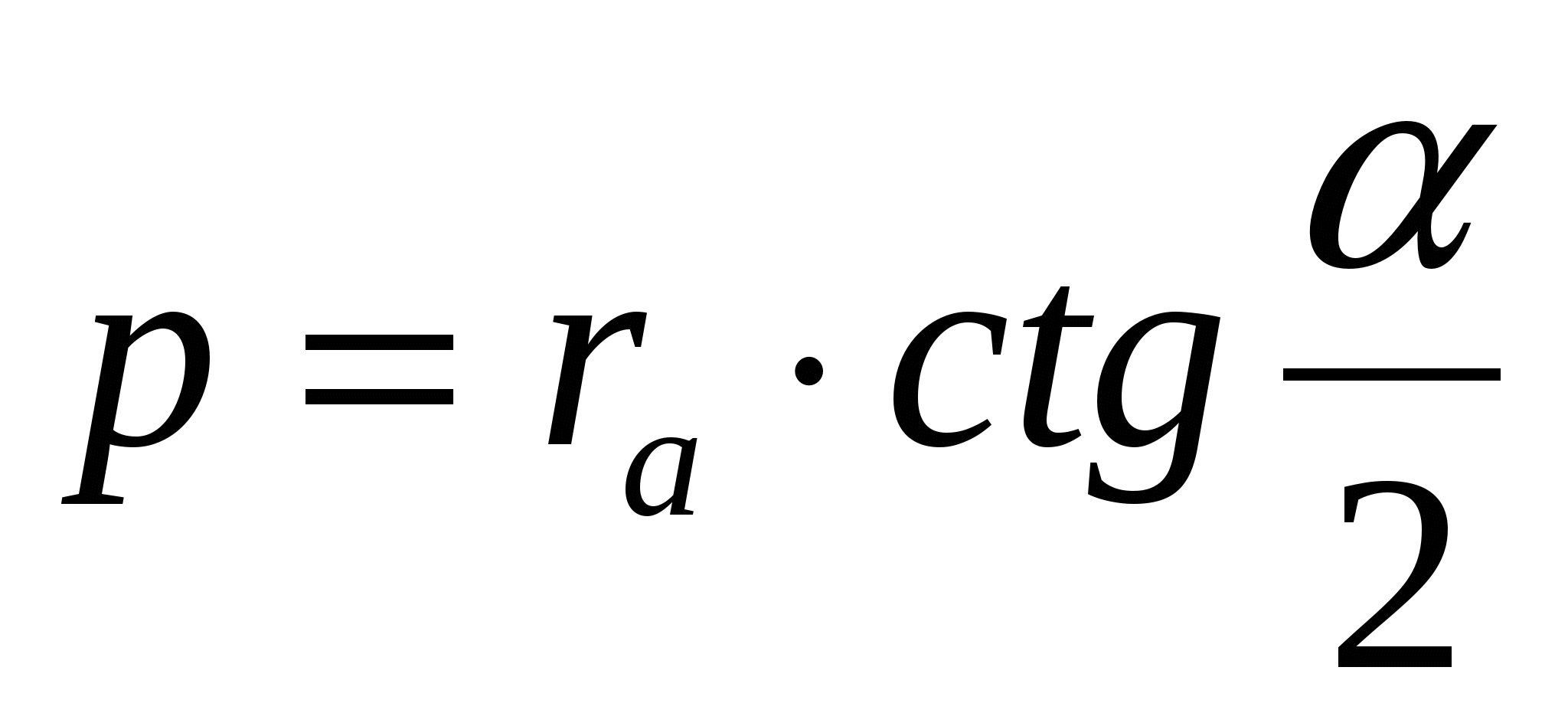
5. Четырехугольник ABCD обладает тем свойством, что существует окружность, вписанная в угол BAD и касающаяся продолжений сторон ВС и CD . Докажите, что .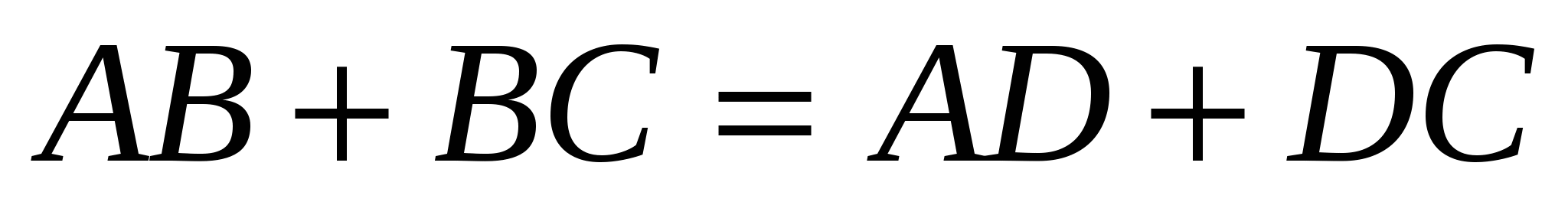

6. Дан параллелограмм ABCD . Вневписанная окружность треугольника ABD касается продолжений сторон AD и AB в точках M и N . Докажите, что точки пересечения отрезка M N с BC и CD лежат на вписанной окружности треугольника BCD .

7. Пусть a и b две стороны треугольника. Как подобрать третью сторону с так, чтобы точки касания вписанной и вневписанной окружностей со стороной с делили эту сторону на три равных отрезка? При каких a и b такая сторона с существует?

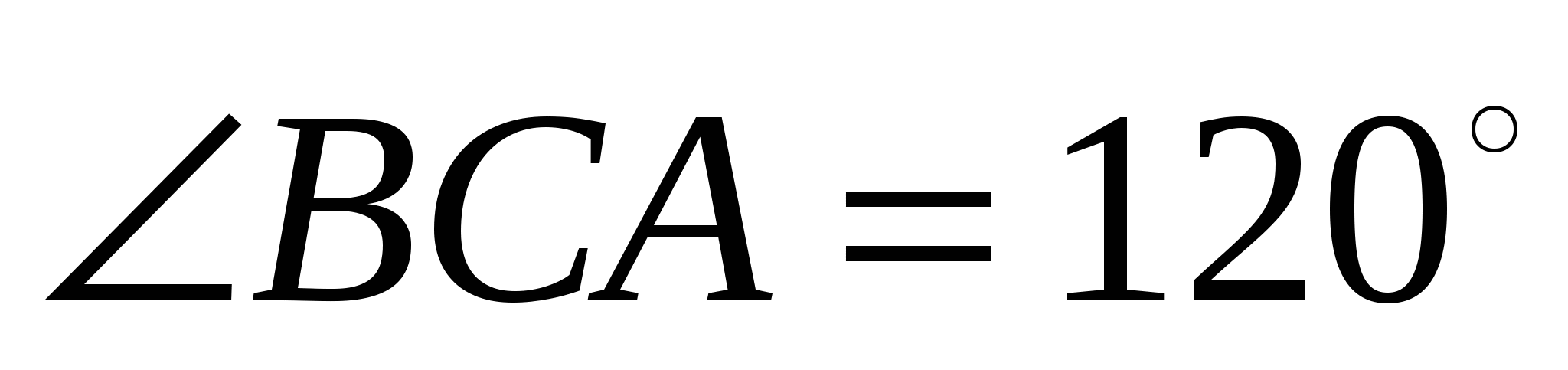
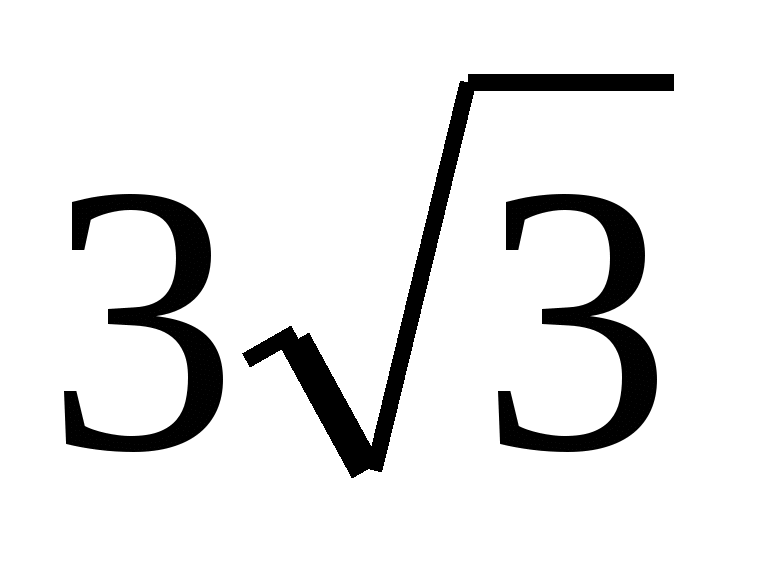
8. Окружность радиуса 3, вписанная в треугольник ABC , касается стороны BC в точке Е. Окружность радиуса 4 касается продолжения сторон АВ и АС и касается стороны ВС в точке D . Найдите длину отрезка ED , если . Ответ: .

9. С помощью циркуля и линейки постройте точку, равноудаленную от трех данных прямых. (Комментарий: рассмотрите все возможные случаи взаимного расположения трех прямых на плоскости).

10. Отрезок, соединяющий вершину А треугольника ABC с центром Q вневписанной окружности, касающейся стороны ВС, пересекает описанную окружность этого треугольника в точке D . Докажите, что треугольник BDQ – равнобедренный.

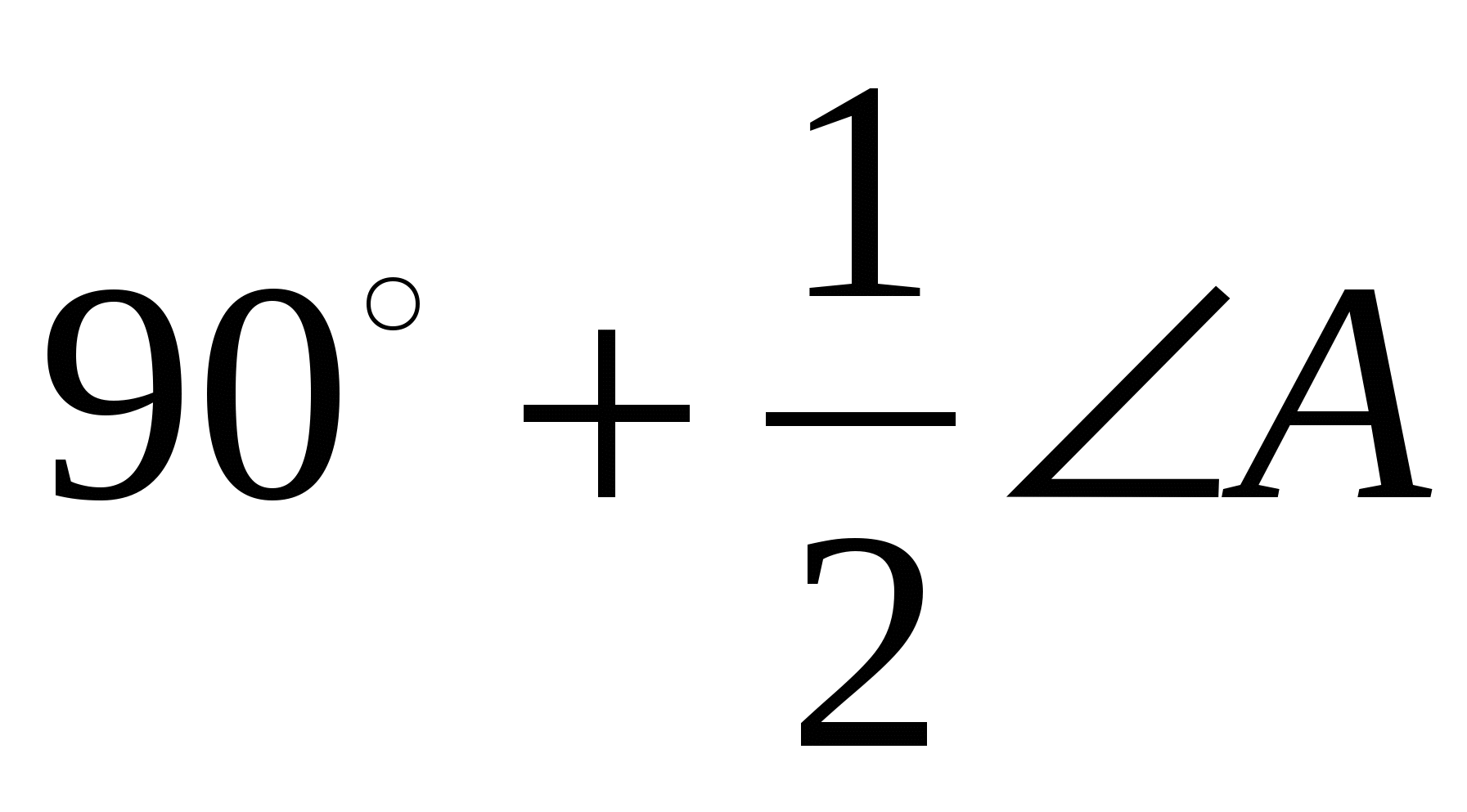
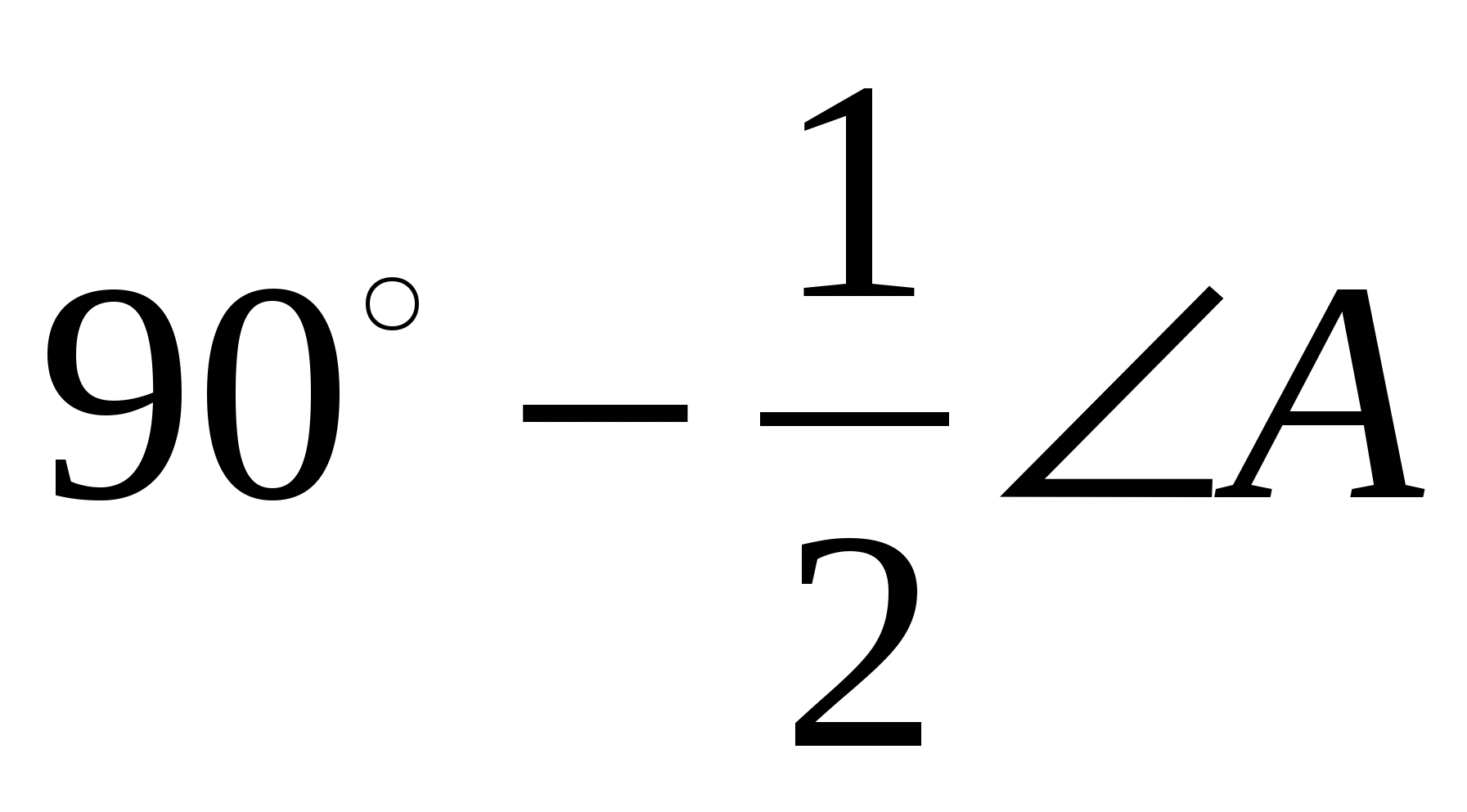
11. Докажите, что сторона ВС треугольника ABC видна из центра О вписанной окружности под углом , а из центра О₁ вневписанной окружности, касающейся стороны ВС, — под углом .

12. Доказать, что для любого треугольника отрезок, соединяющий центры вписанной и вневписанной окружности, делятся описанной окружностью пополам.

13. Вписанная окружность треугольника ABC касается стороны АС в точке D ; DM – ее диаметр. Прямая BM пересекает сторону АС в точке К. Докажите, что АК= DC .

14. Сторона правильного треугольника равна а. Найдите радиус вневписанной окружности.

15. Найдите радиусы вписанной и вневписанной окружностей треугольника со сторонами 5, 12, 13.

16. В треугольнике PQR величина угла QRP равна 60º. Найдите расстояние между точками касания со стороной QR окружности радиуса 2, вписанной в треугольник, и окружности радиуса 3, касающейся продолжений сторон PQ и PR .

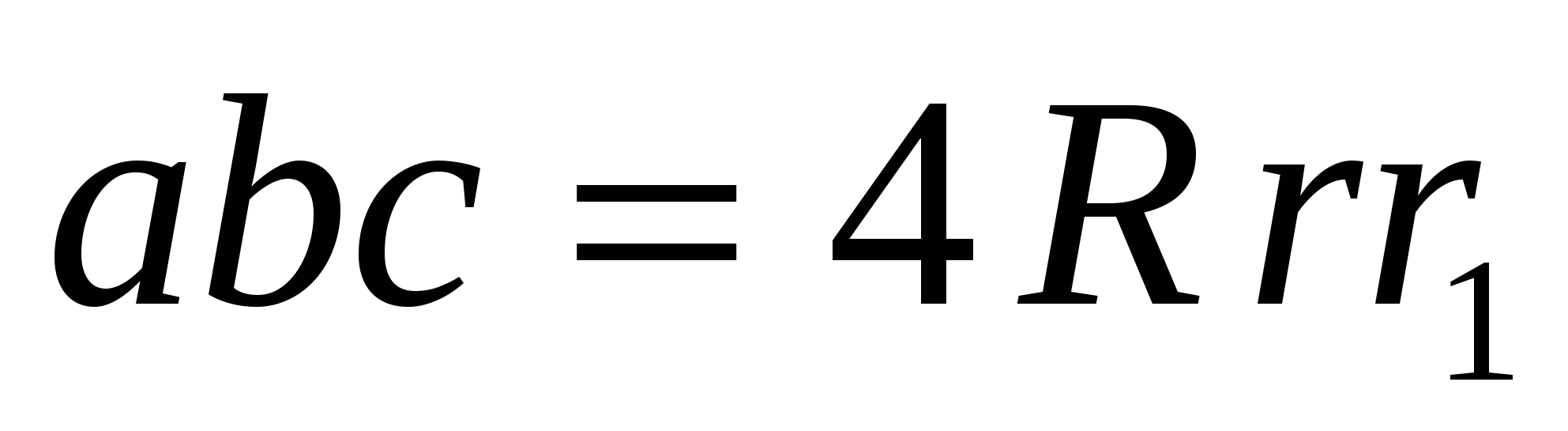
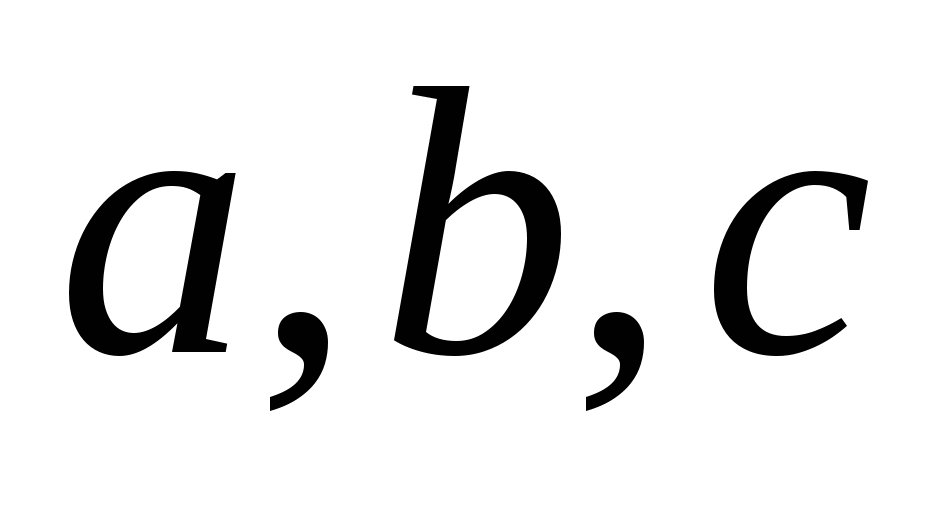
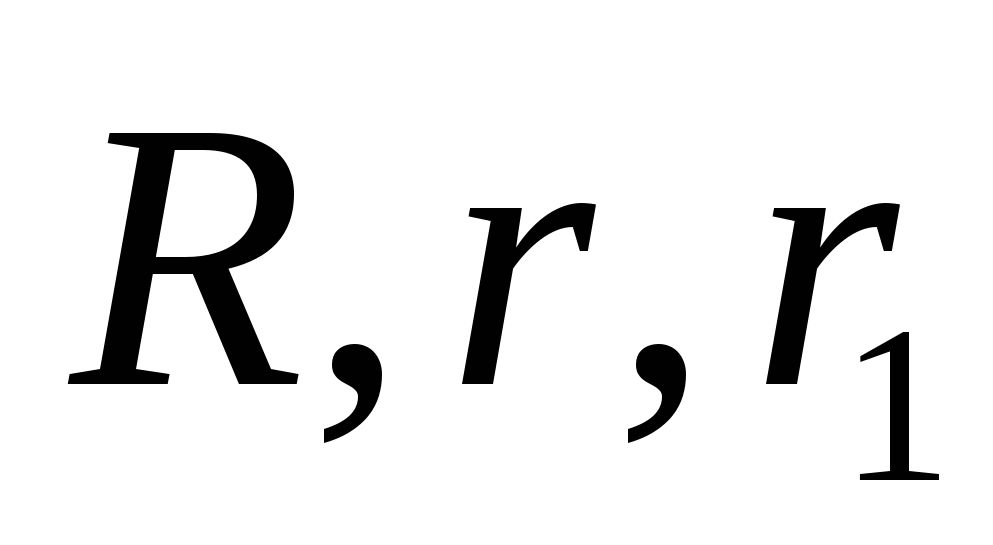
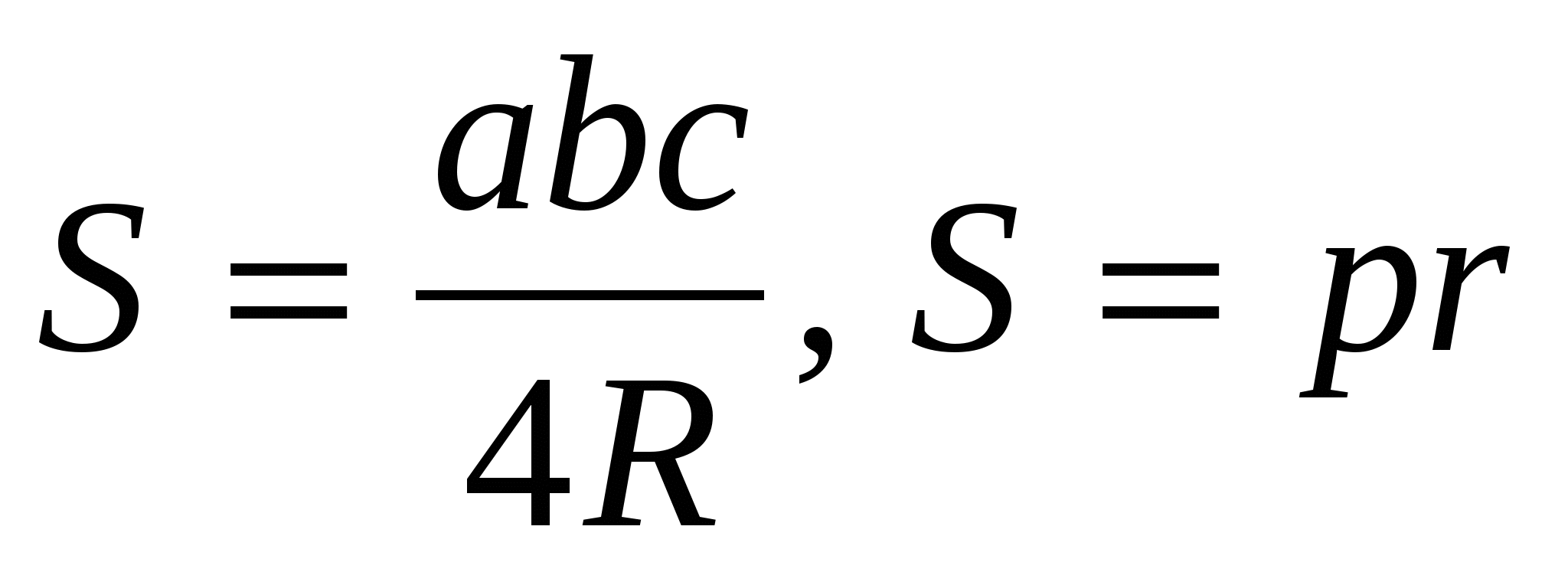
17. Докажите, что если , где — стороны треугольника, — соответственно радиус описанной, вписанной и одной вневписанной окружностей, то треугольник прямоугольный (подсказка: воспользуйтесь формулами ).

18. Сторона квадрата ABCD равна 1. На сторонах AB и А D выбраны точки P и Q так, что периметр треугольника APQ равен 2. Докажите, что 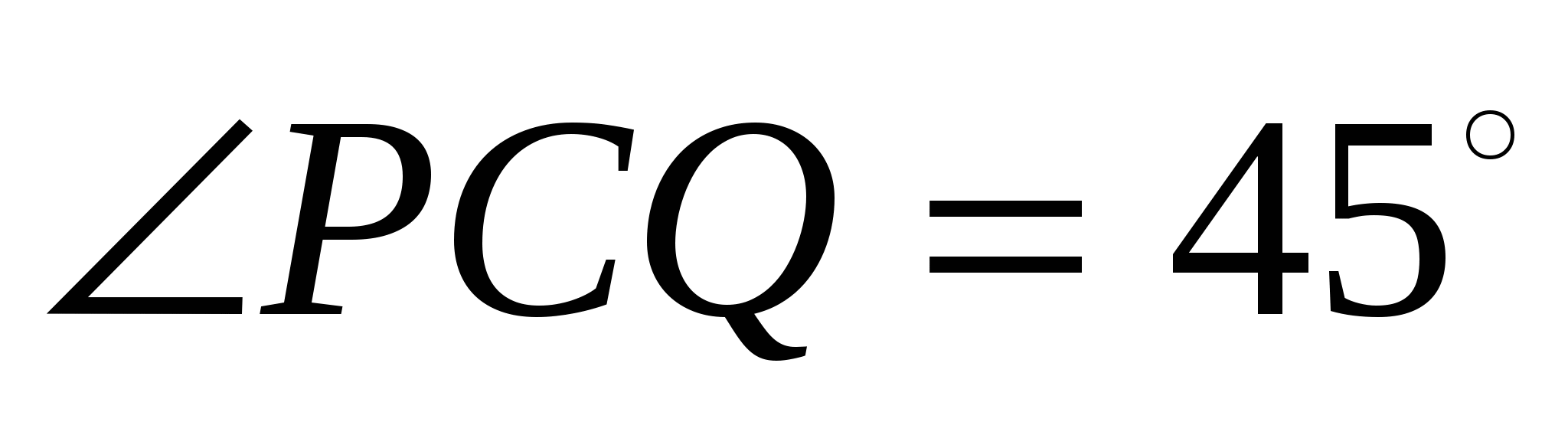(подсказка: рассмотрите вневписанную окружность треугольника APQ ).

19. В треугольнике ABC с периметром 2р величина острого угла BAC равна α. Окружность с центром в точке О касается стороны ВС и продолжения сторон АВ и АС в точках K , L и M соответственно. Точка D лежит внутри отрезка АК, AD = а. Найдите площадь треугольника DOK .

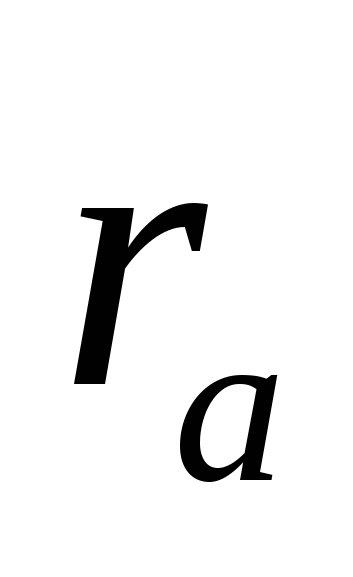
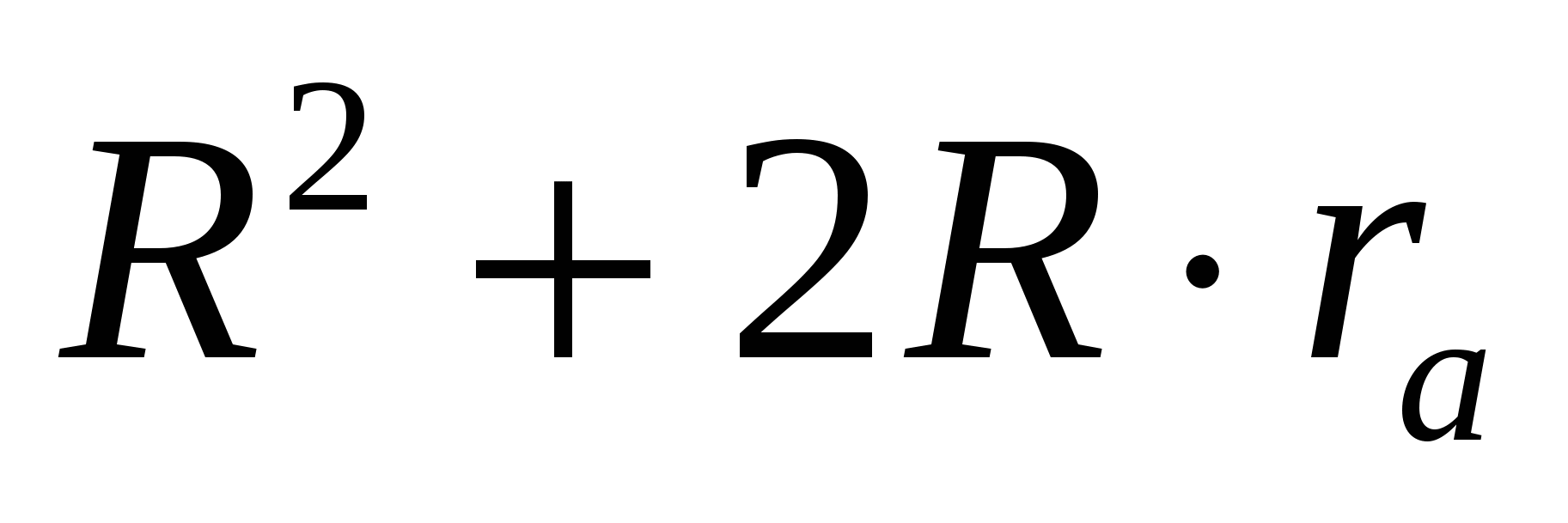
20. Пусть R — радиус описанной окружности треугольника ABC , — радиус вневписанной окружности, касающейся стороны ВС. Докажите, что квадрат расстояния между центрами этих окружностей равен .

21. С помощью циркуля и линейки постройте треугольник по центрам описанной и одной из вневписанных окружностей (подсказка: описанная окружность треугольника делит пополам отрезок, соединяющий центры вписанной и вневписанной окружностей).

22. Докажите, что если радиус вневписанной окружности равен полупериметру треугольника, то этот треугольник прямоугольный.

23. Через данную точку проведите прямую, отсекающую от данного угла треугольник наименьшего возможного периметра.

24. В основании пирамиды лежит правильный треугольник со стороной а. Двугранные углы между основанием и плоскостями боковых граней равны α. Найдите угол между боковыми гранями.

Решение некоторых задач из приложения

1. Доказать, что:

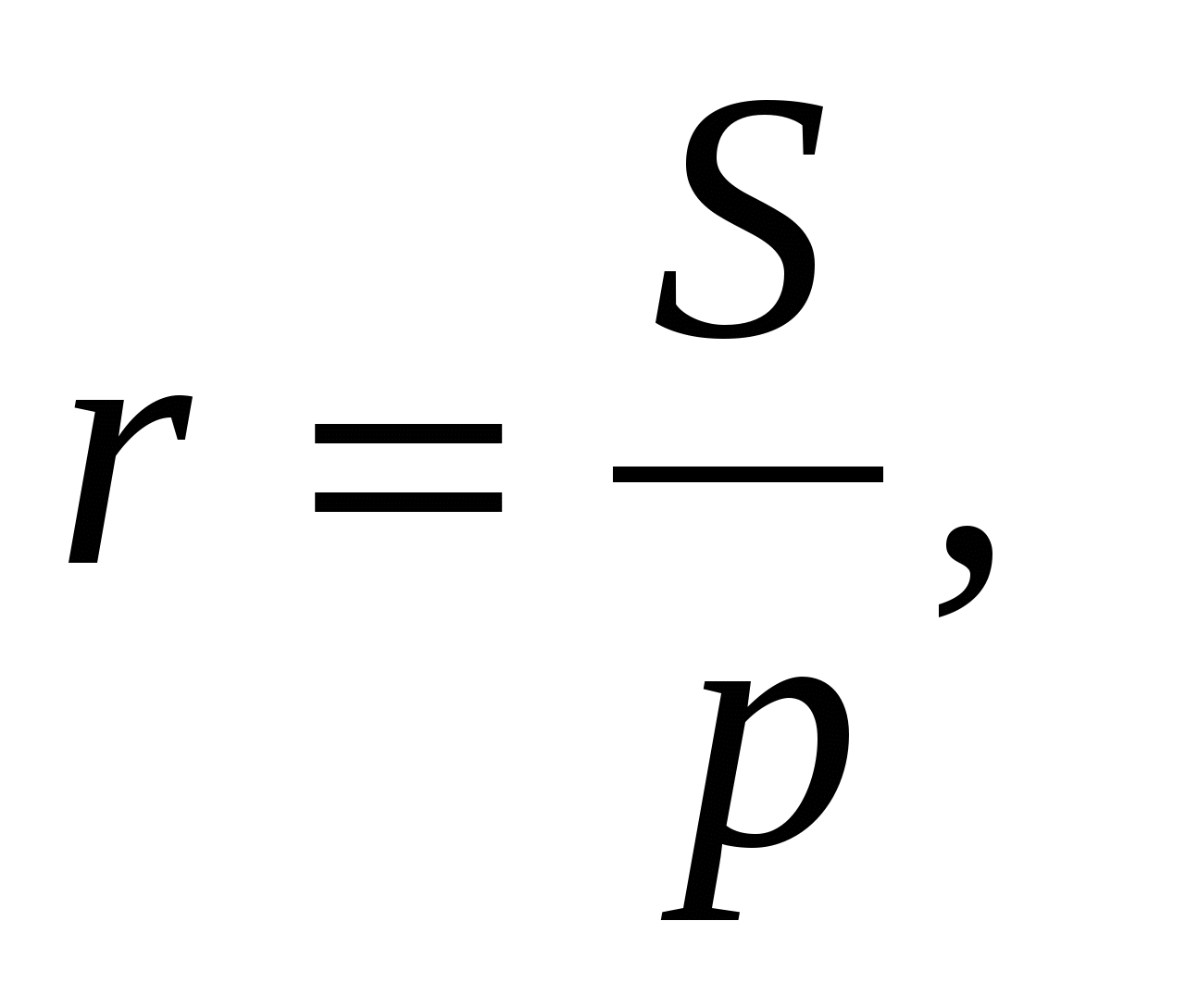
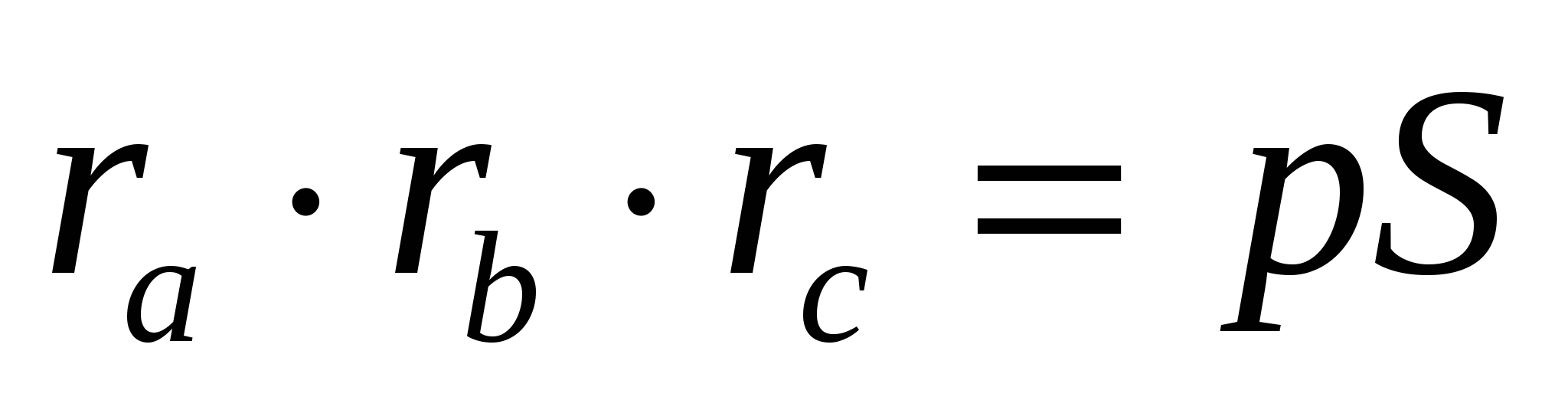
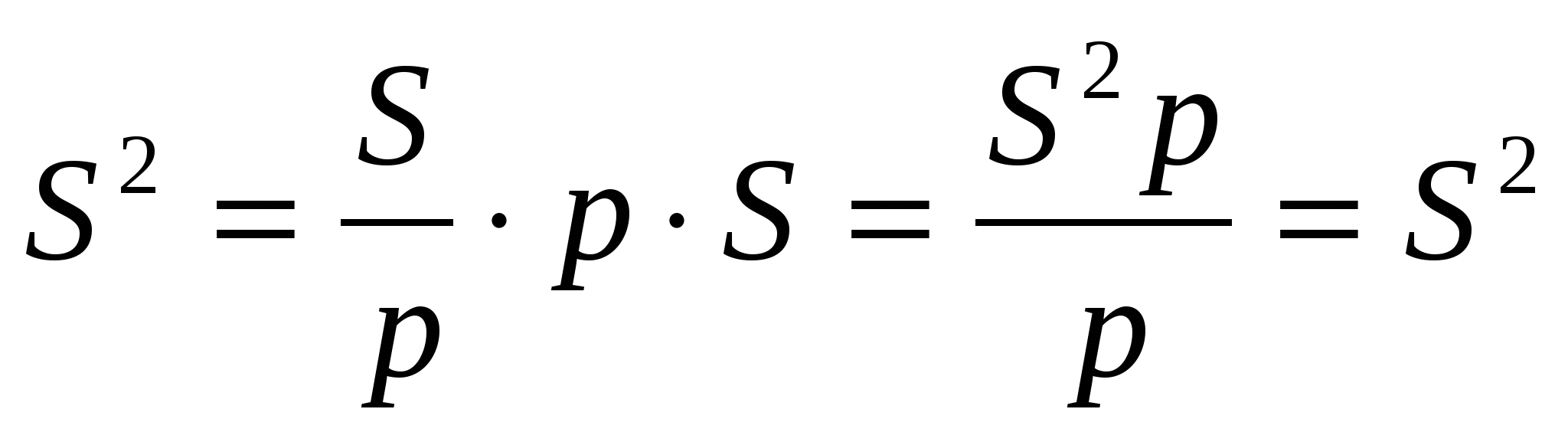
Доказательство: так как а , то , ч.т.д.

2. Доказать, что: .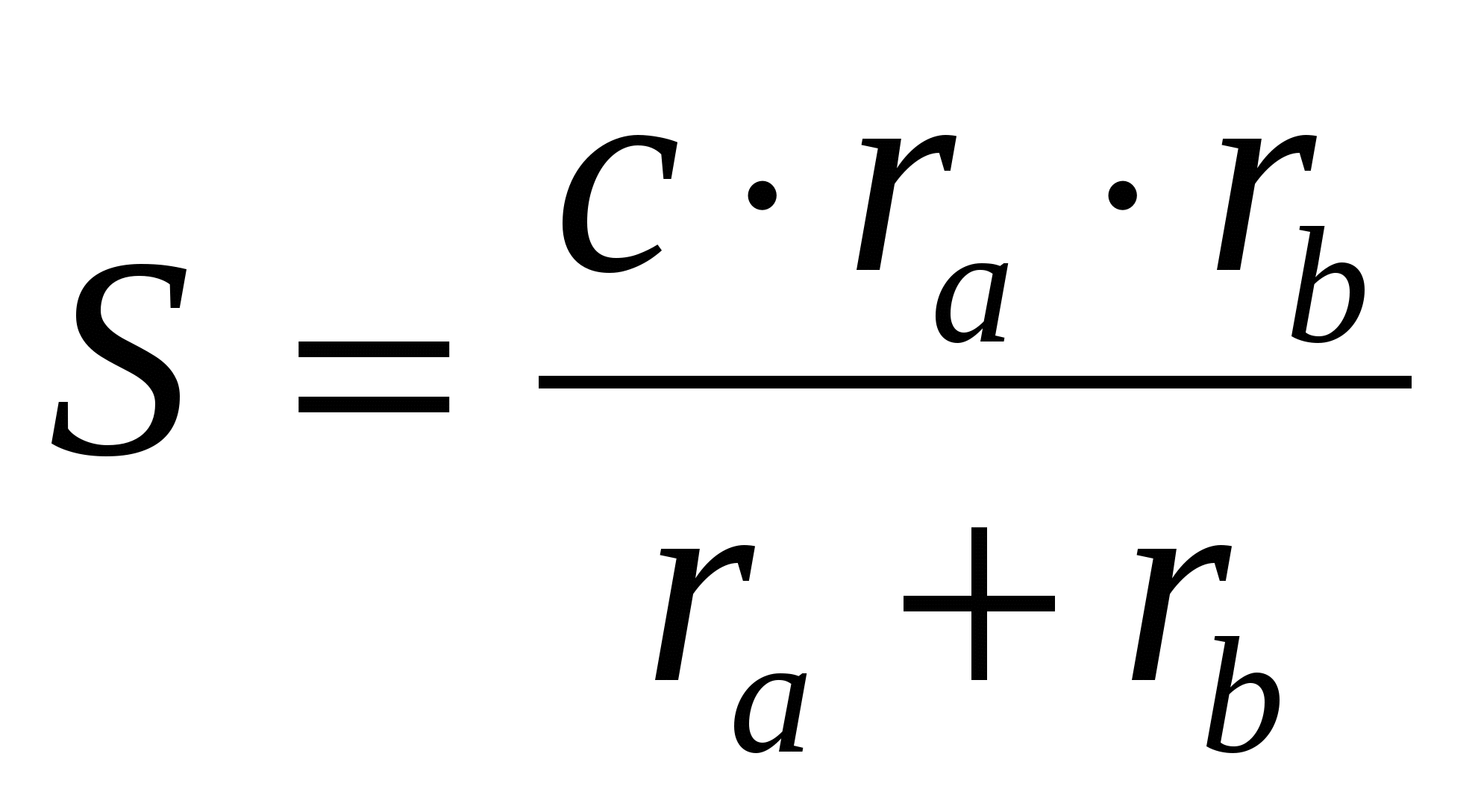

1) ,

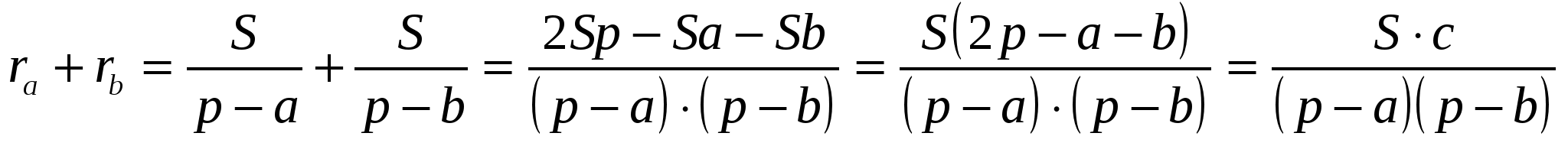
так как ;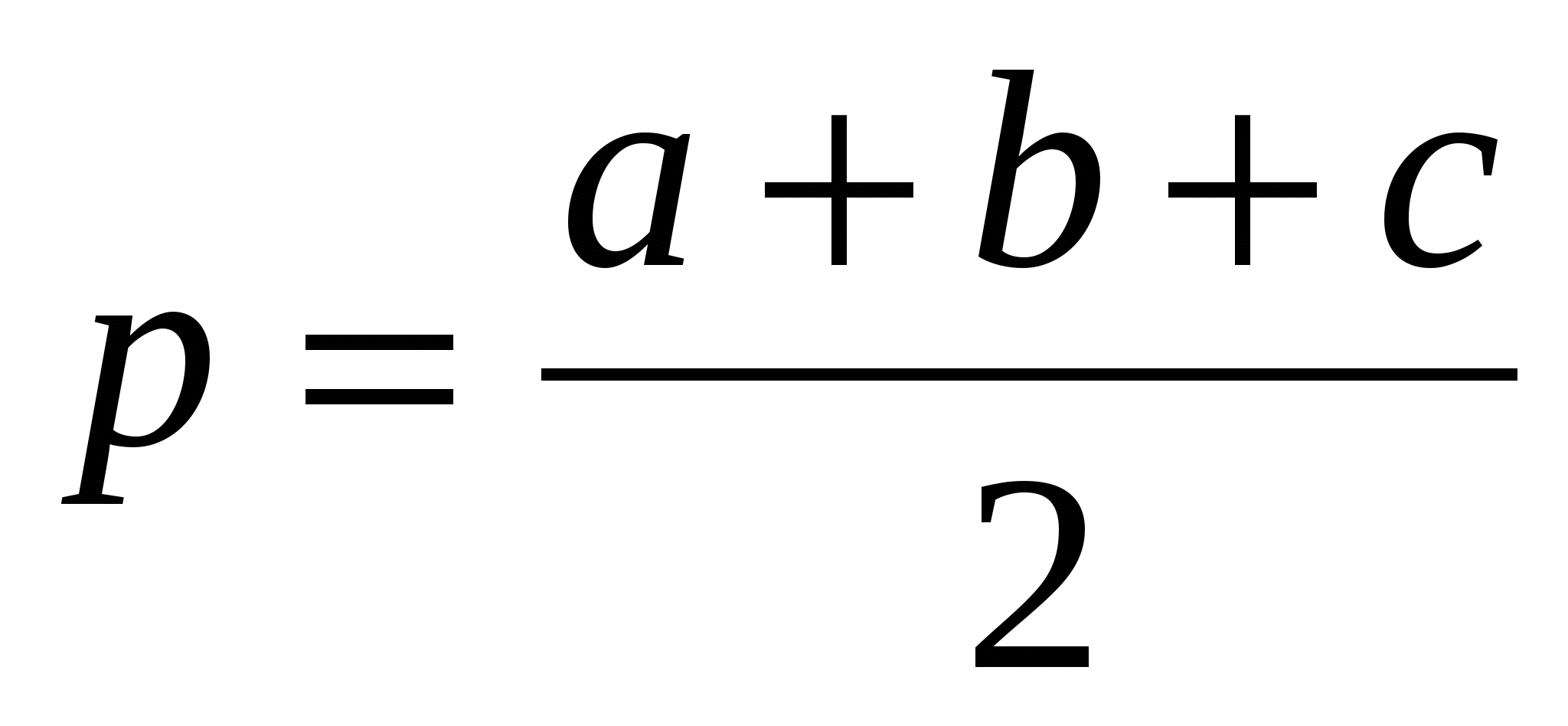

2) ;

, ч.т.д.

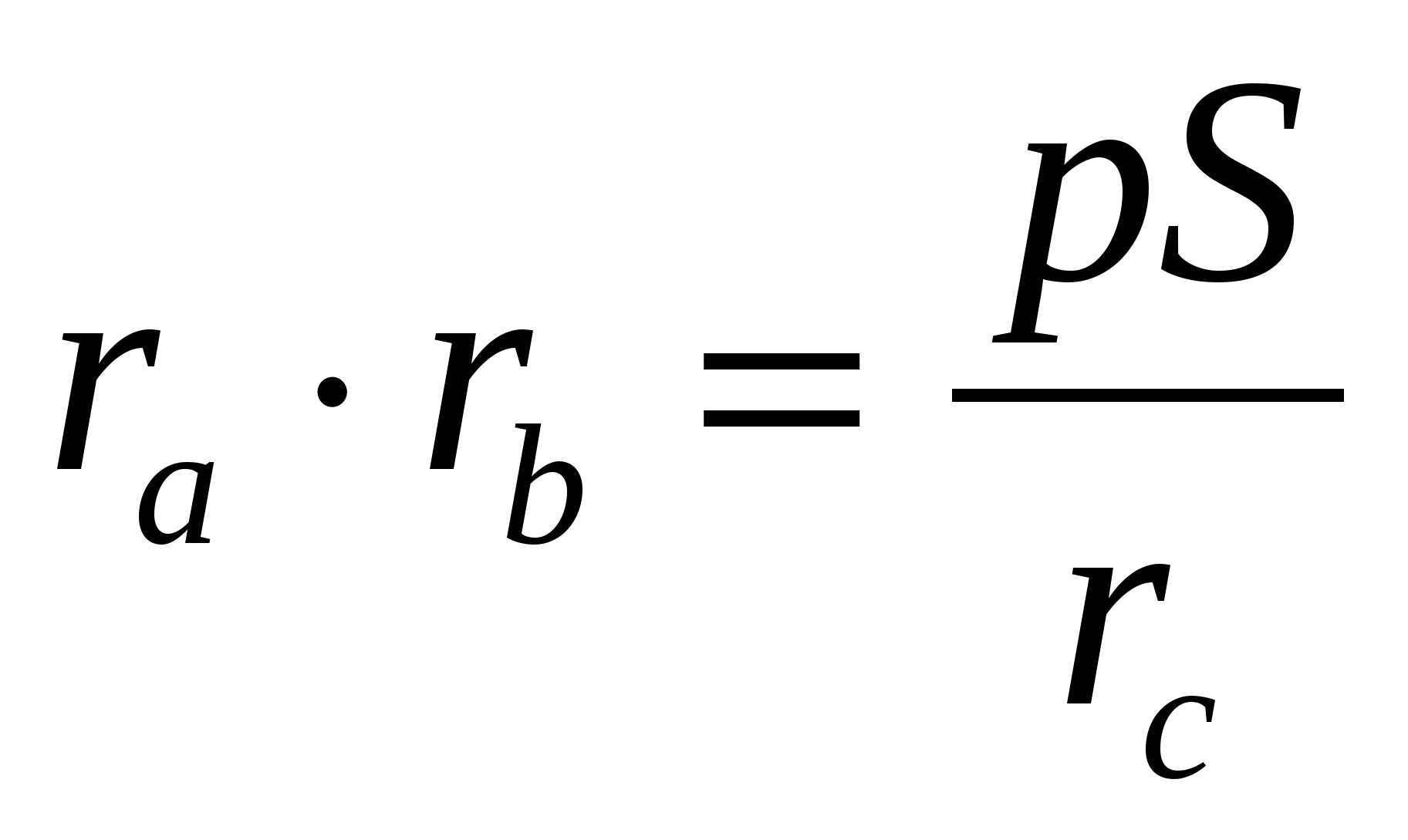
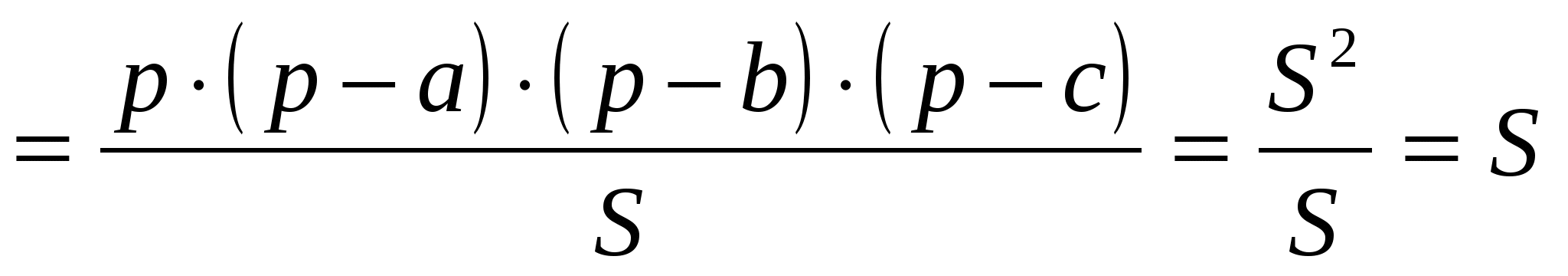
3. Доказать, что: .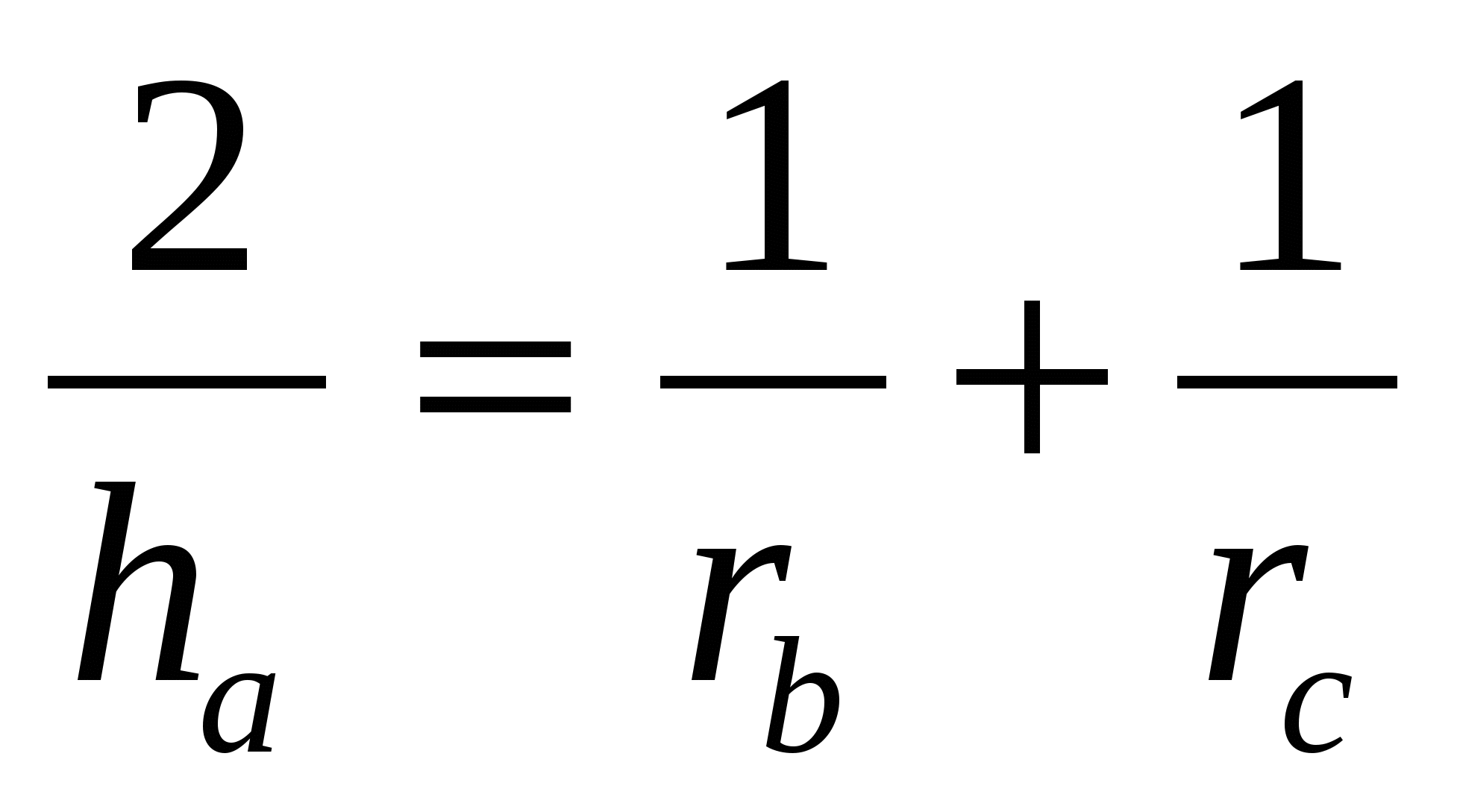

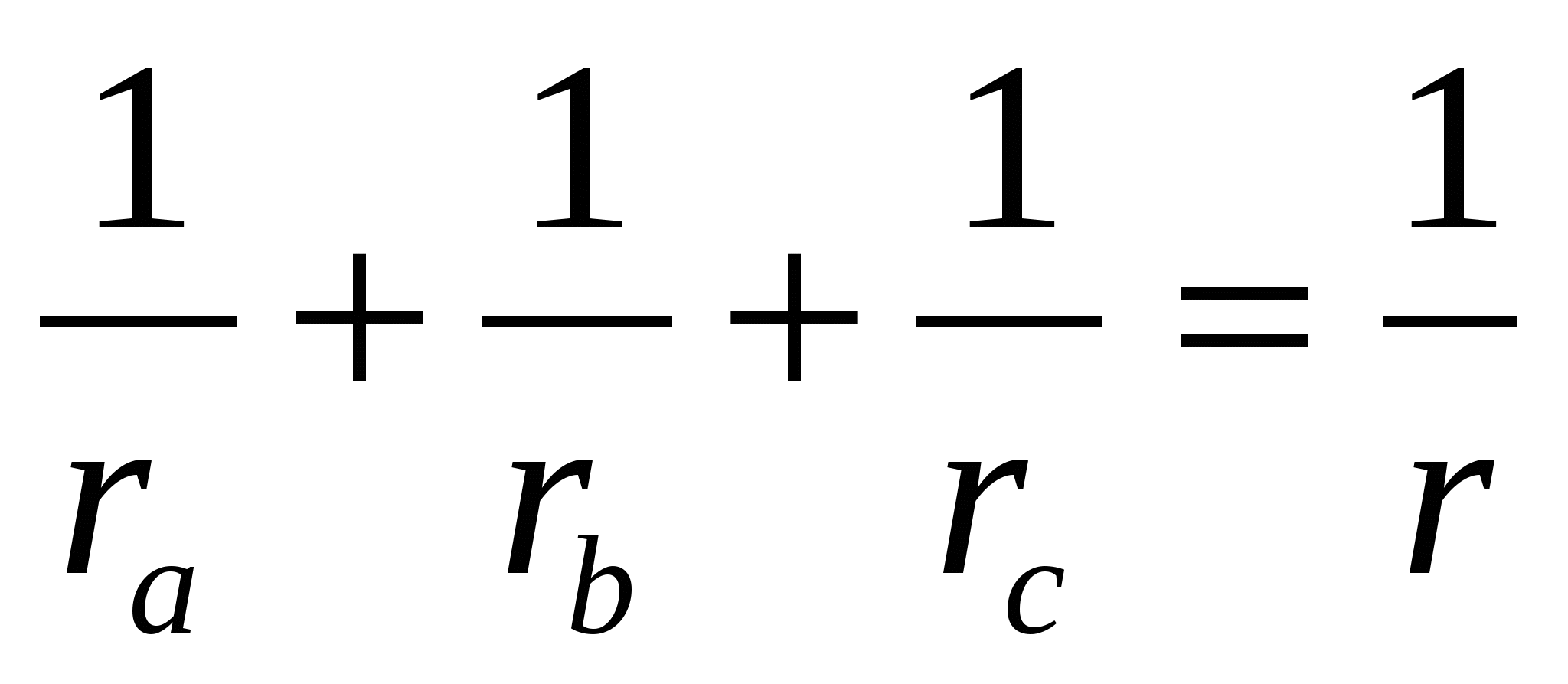
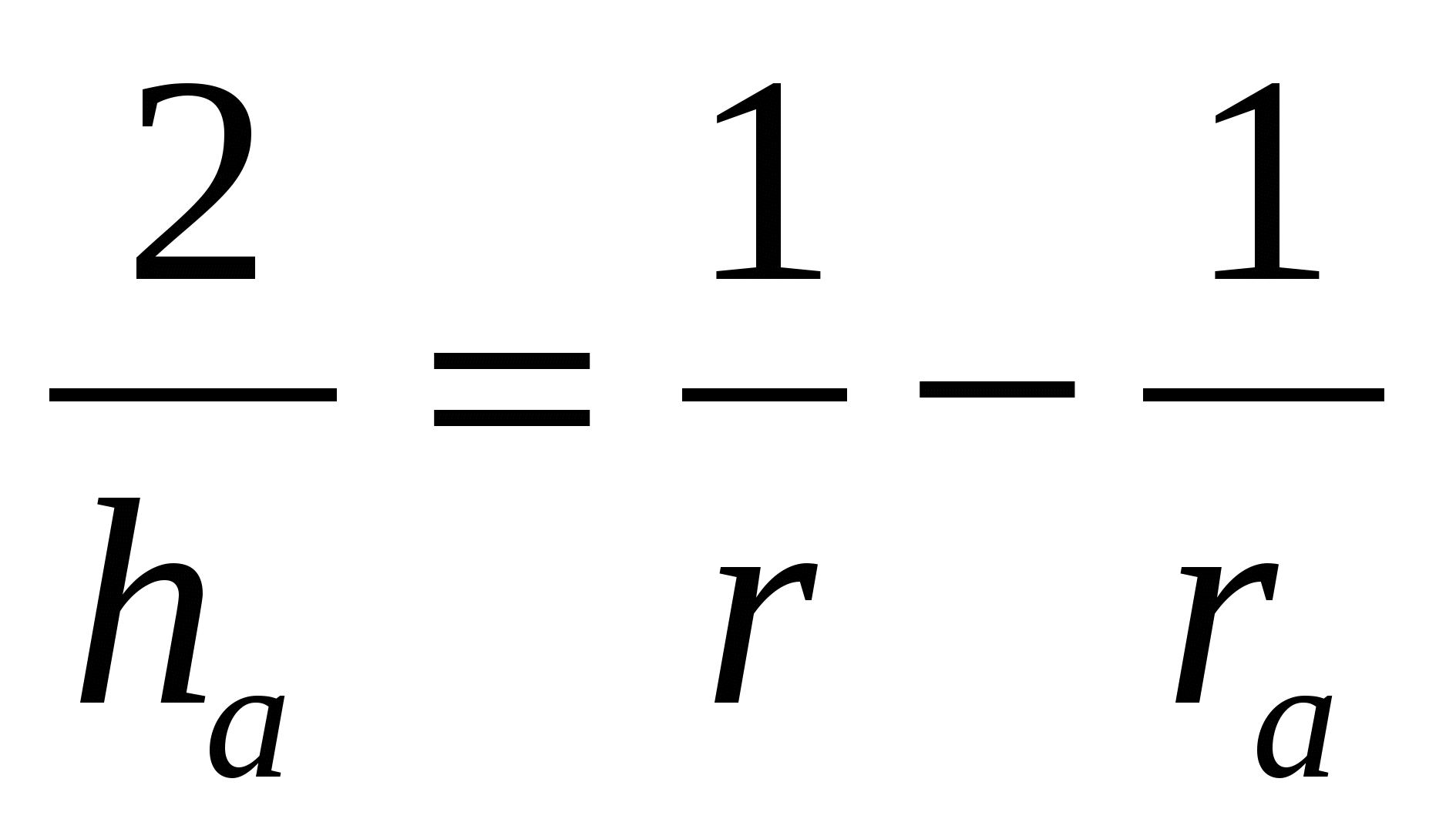
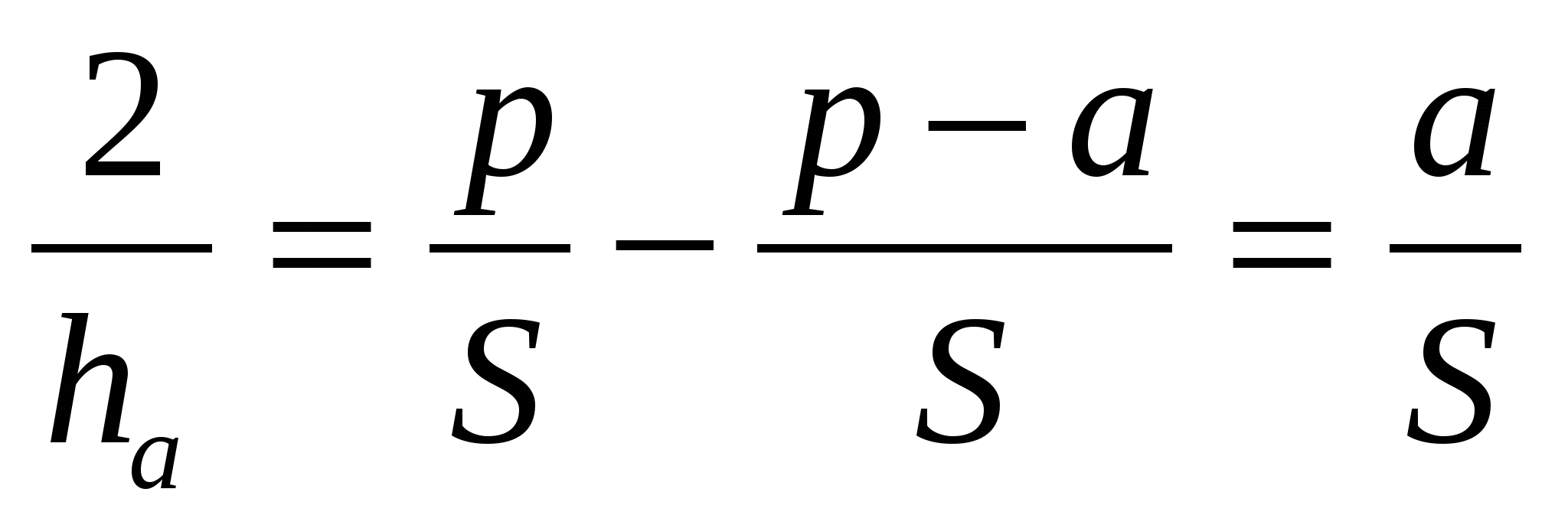
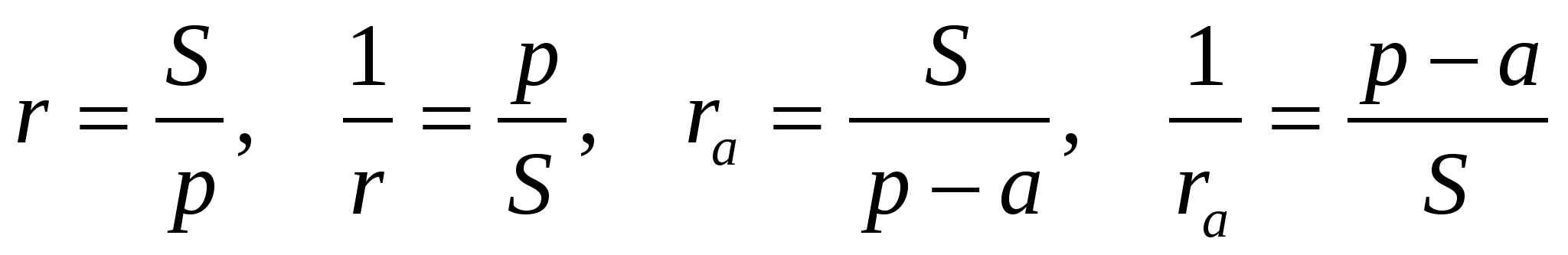
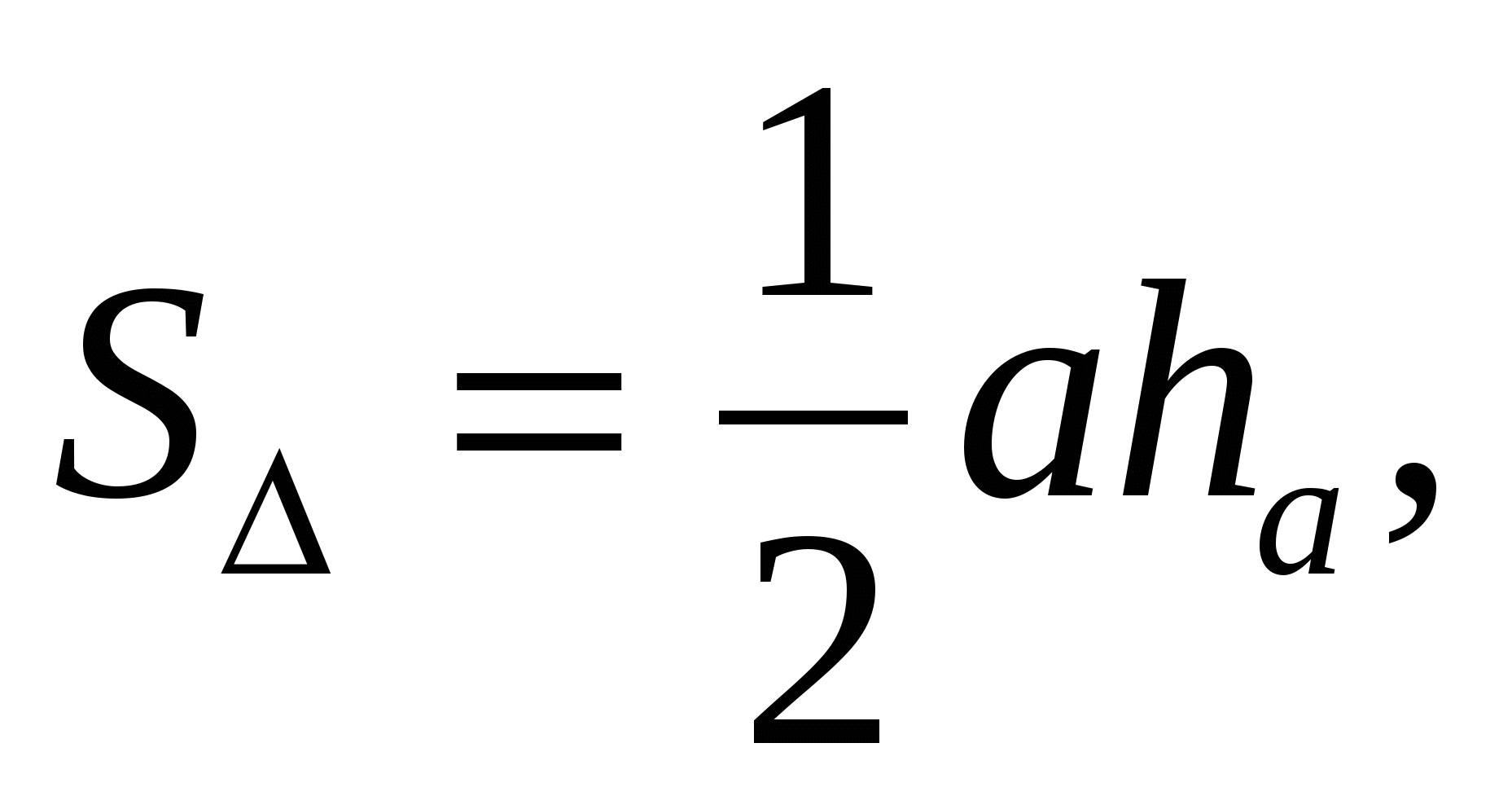
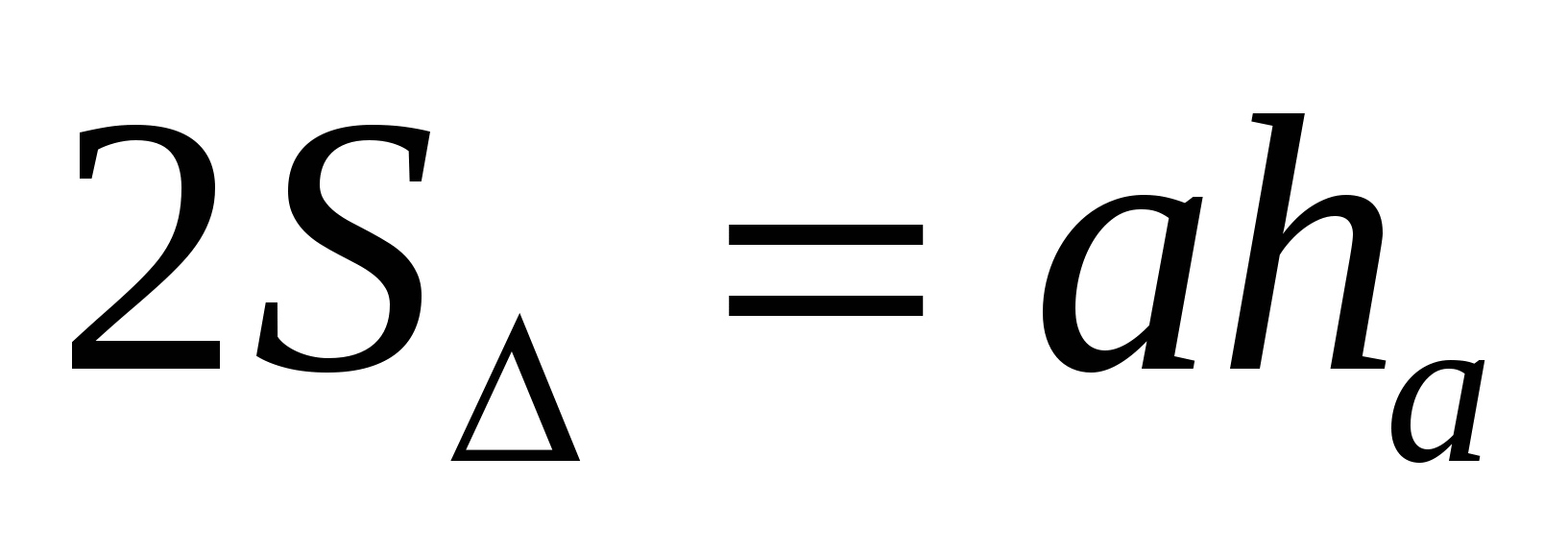
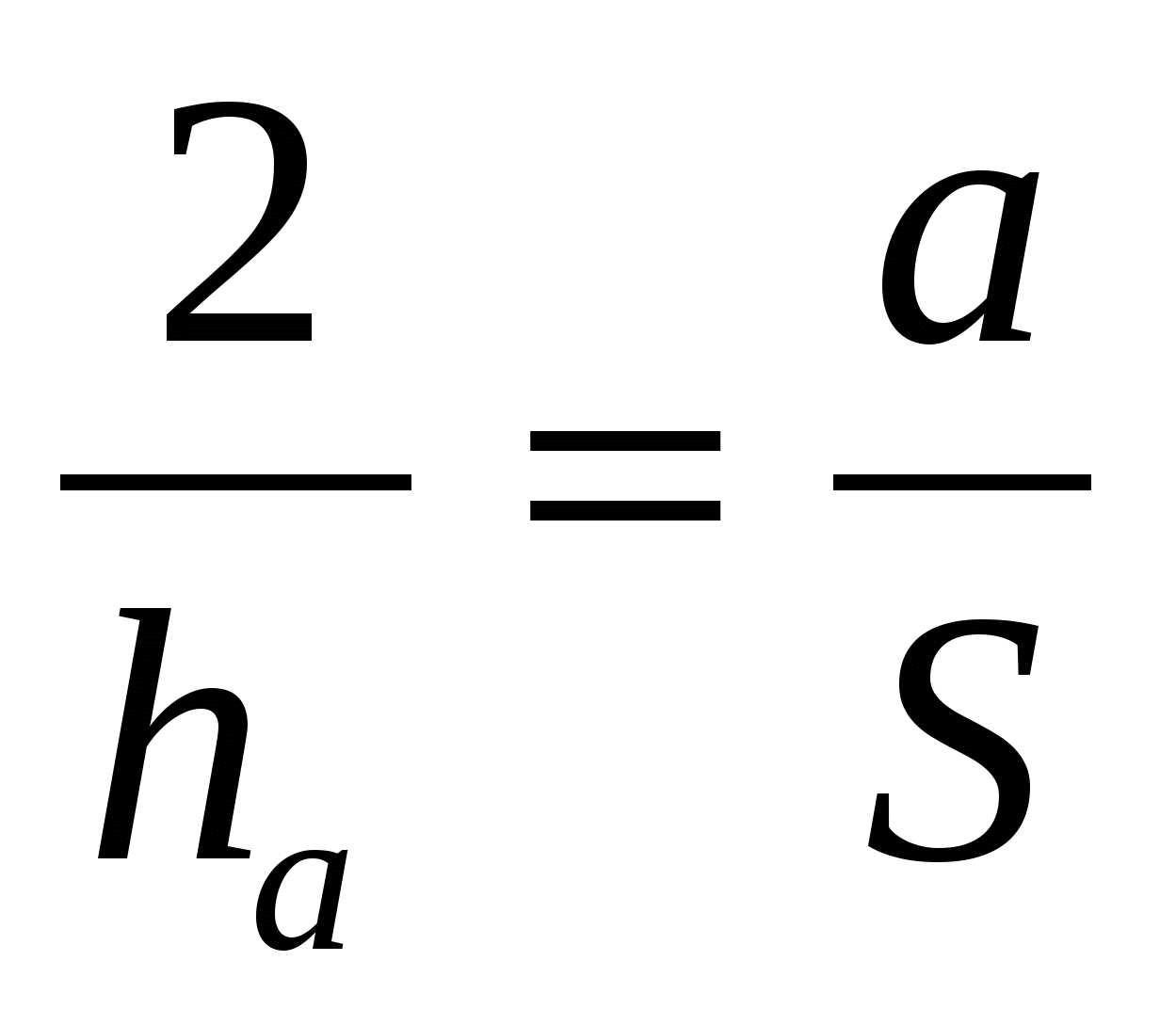
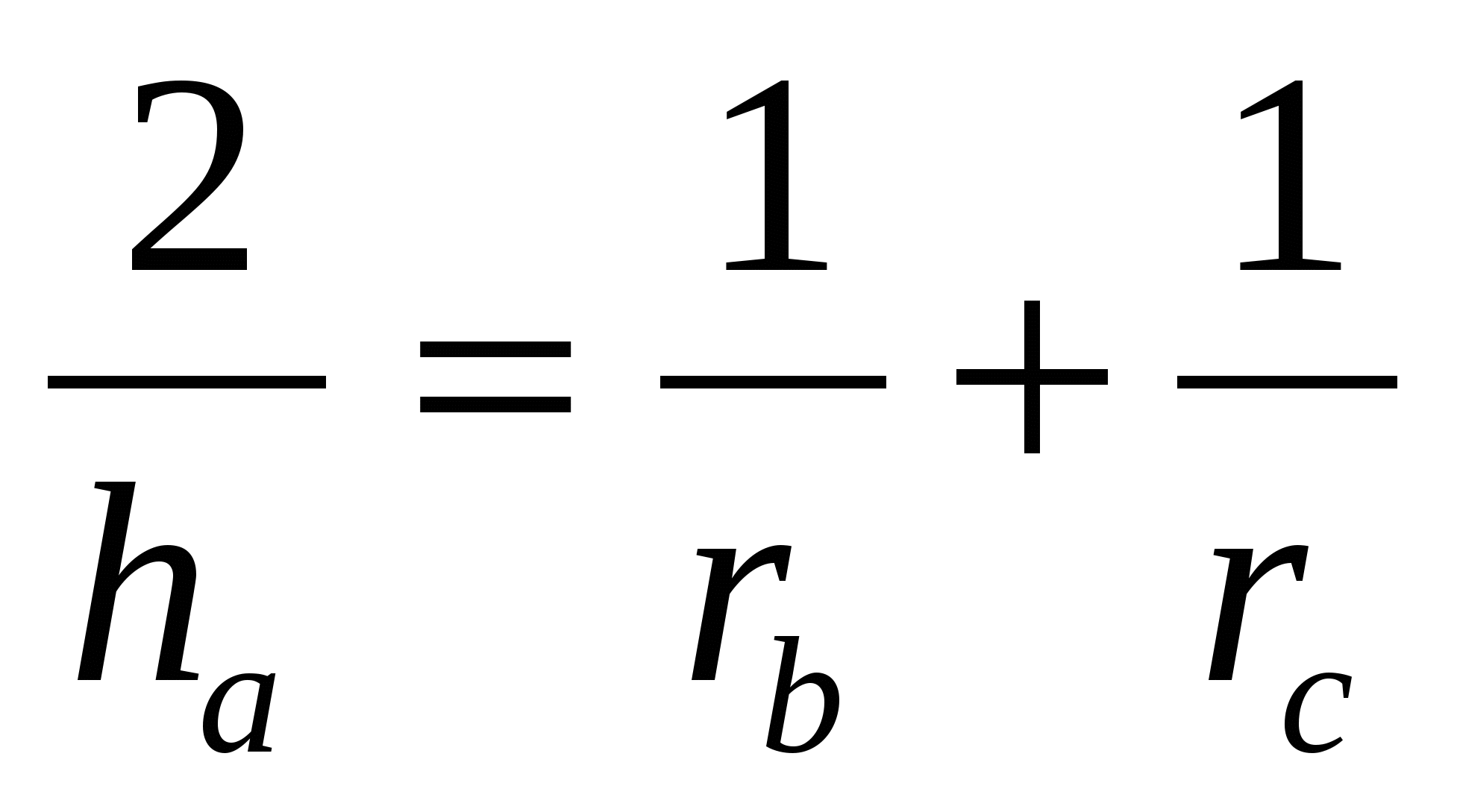
Доказательство: Так как , то . Тогда (с использованием формул ).

и . Таким образом, .

9. С помощью циркуля и линейки постройте точку, равноудаленную от трех данных прямых. (Комментарий: рассмотрите все возможные случаи взаимного расположения трех прямых на плоскости).

1) Если все три прямые параллельны, то решений нет.

2) Если все три прямые пересекаются в одной точке, то эта точка является искомой.

3) Если две параллельные прямые пересекаются третьей, то задача имеет два решения.

a

4) Если прямые попарно пересекаются, то при пересечении они образуют треугольник и задача имеет четыре решения. В этом случае искомые точки – это центры вписанной в треугольник окружности и трех его вневписанных окружностей.

13. Вписанная окружность треугольника ABC касается стороны АС в точке D ; DM – ее диаметр. Прямая BM пересекает сторону АС в точке К. Докажите, что АК= DC .

Решение: Рассмотрим гомотетию с центром в точке В, переводящую вписанную окружность треугольника ABC в его вневписанную окружность, касающейся стороны АС.

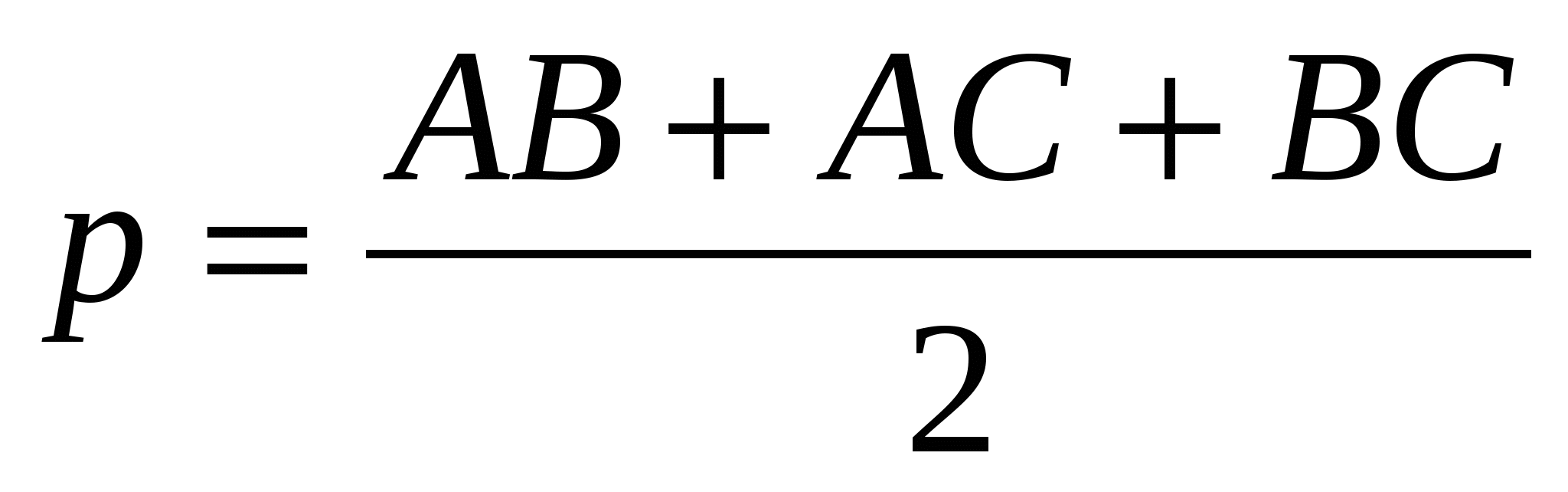
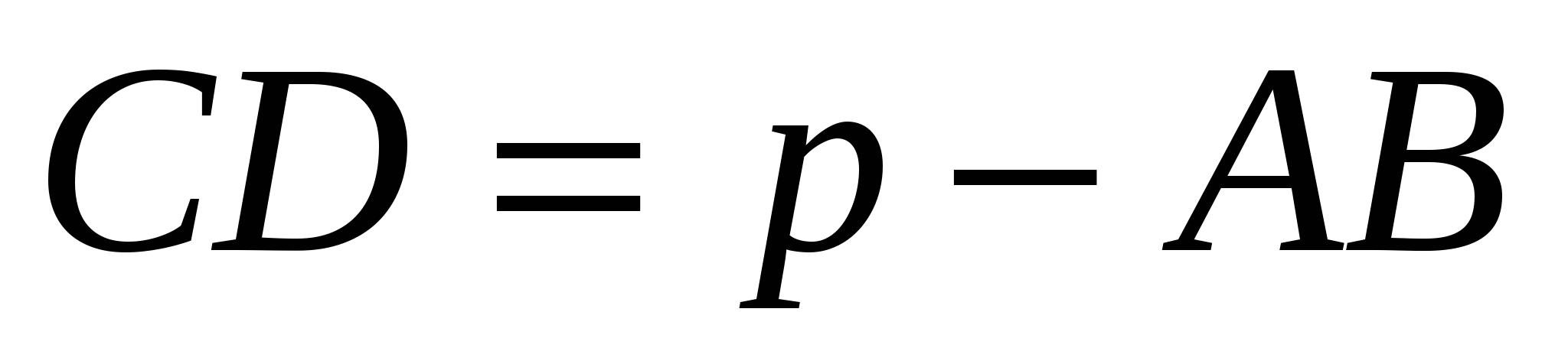
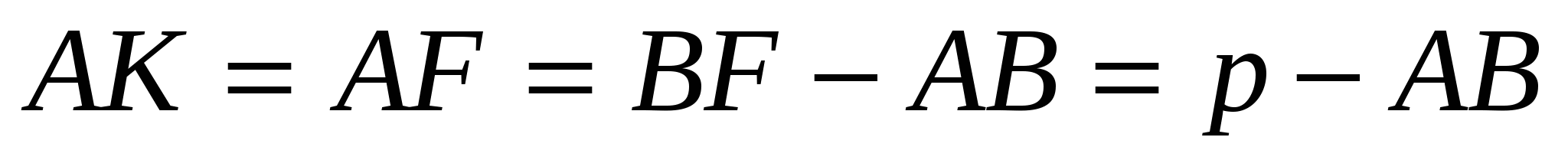
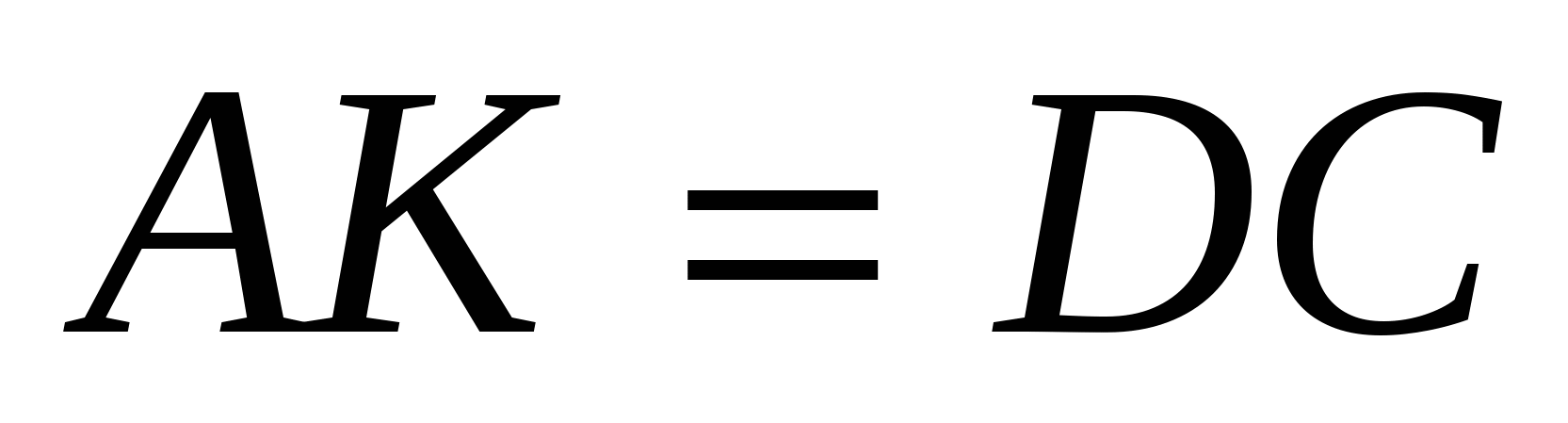
Диаметр вневписанной окружности, соответствующий диаметру DM вписанной окружности касается стороны АС в точке К. Если , F – точка касания вневписанной окружности с лучом ВА, то и . Следовательно .

14. Сторона правильного треугольника равна а. Найдите радиус его вневписанной окружности.

C

Так как треугольник АВС равносторонний, то радиусы всех трех его вневписанных окружностей будут равны. Пусть О_с — центр вневписанной окружности, касающейся стороны АВ треугольника в точке М (середина АВ) и продолжений сторон АС и СВ в точках L и K соответственно.

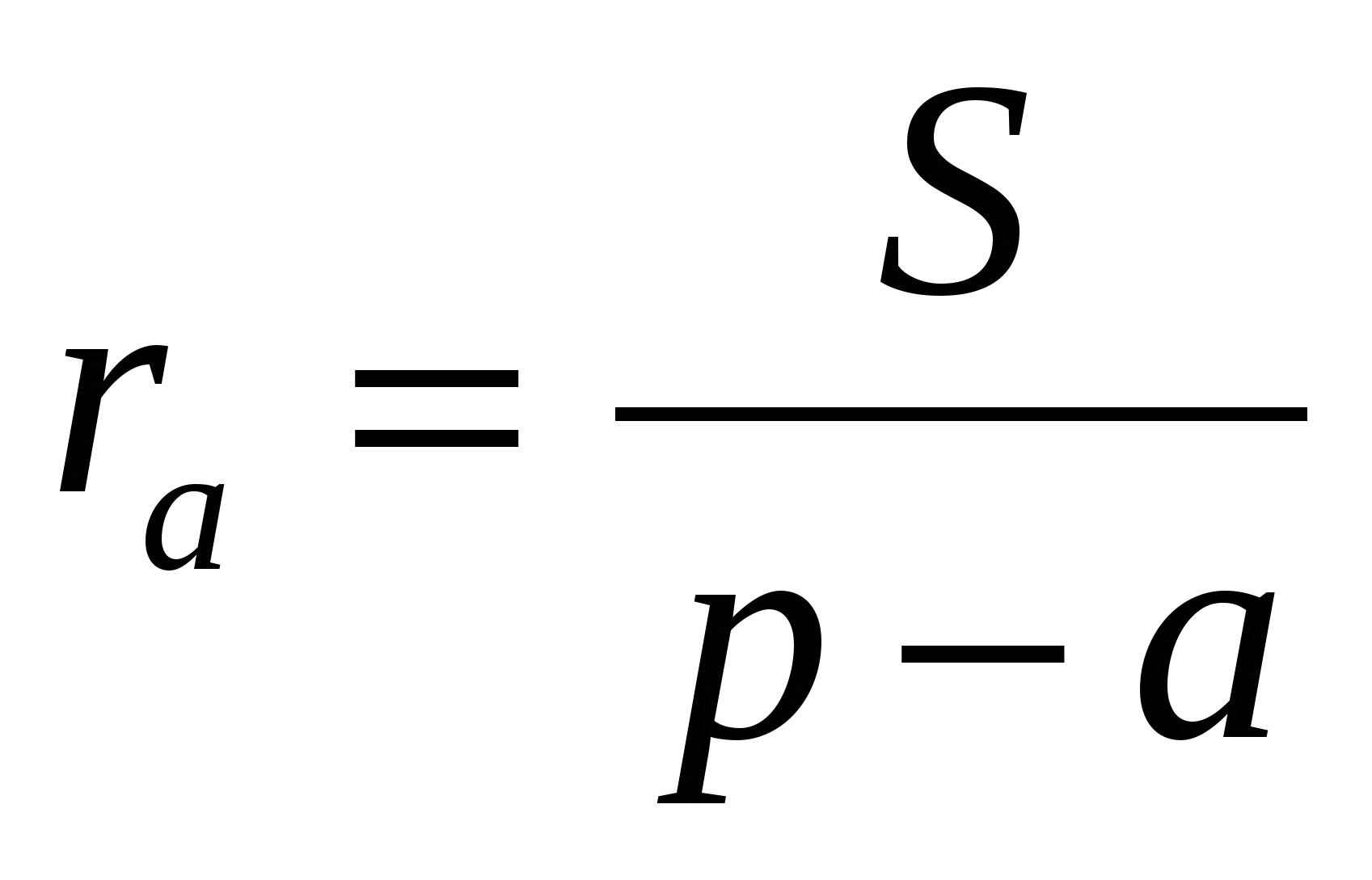
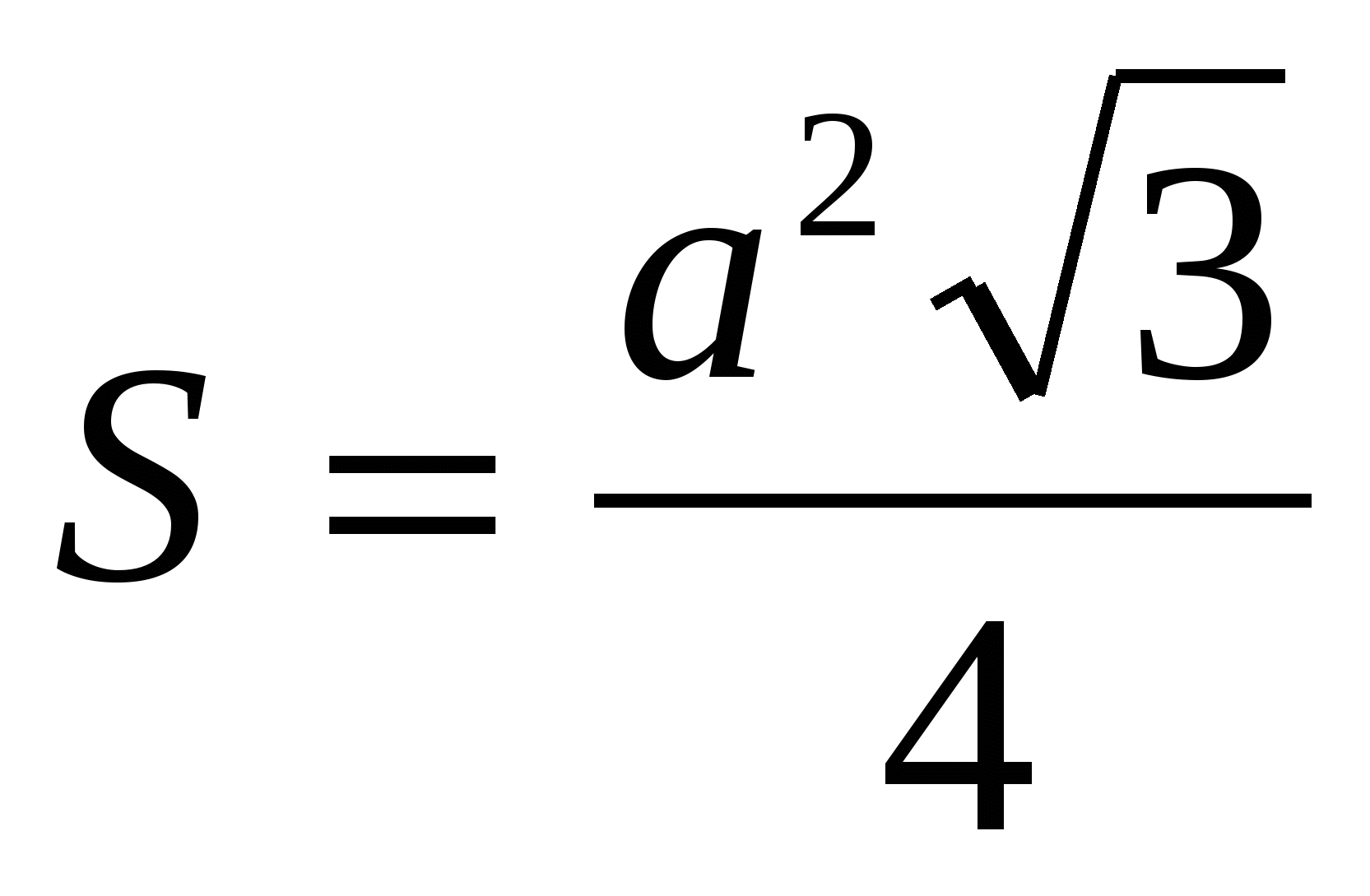
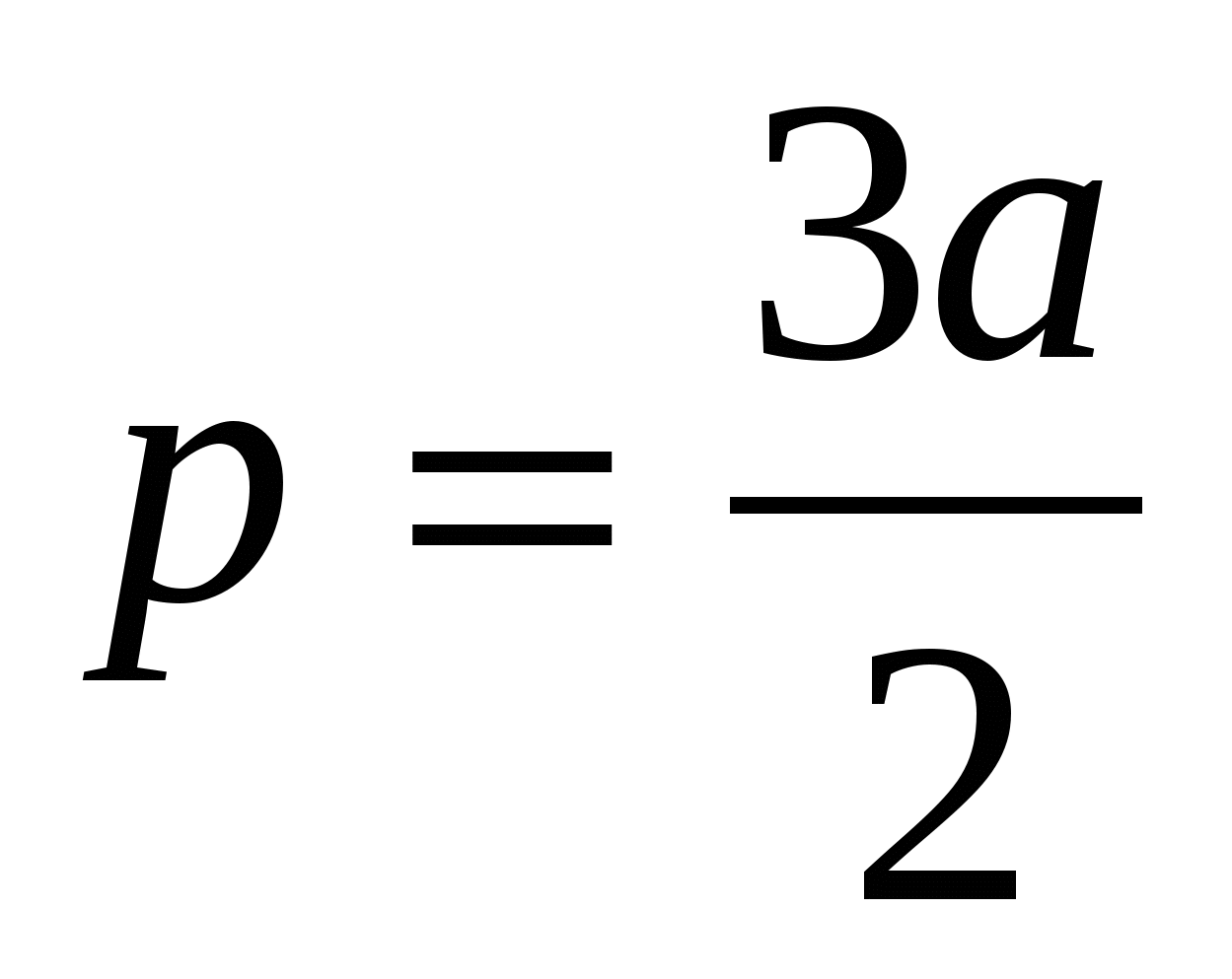
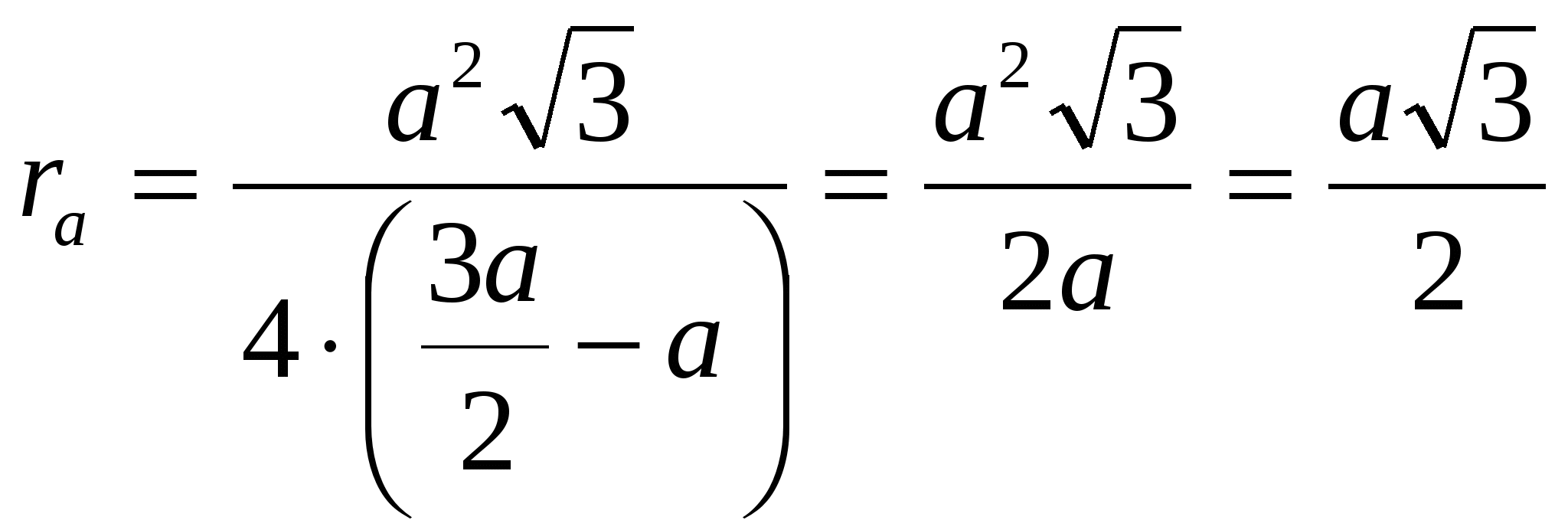
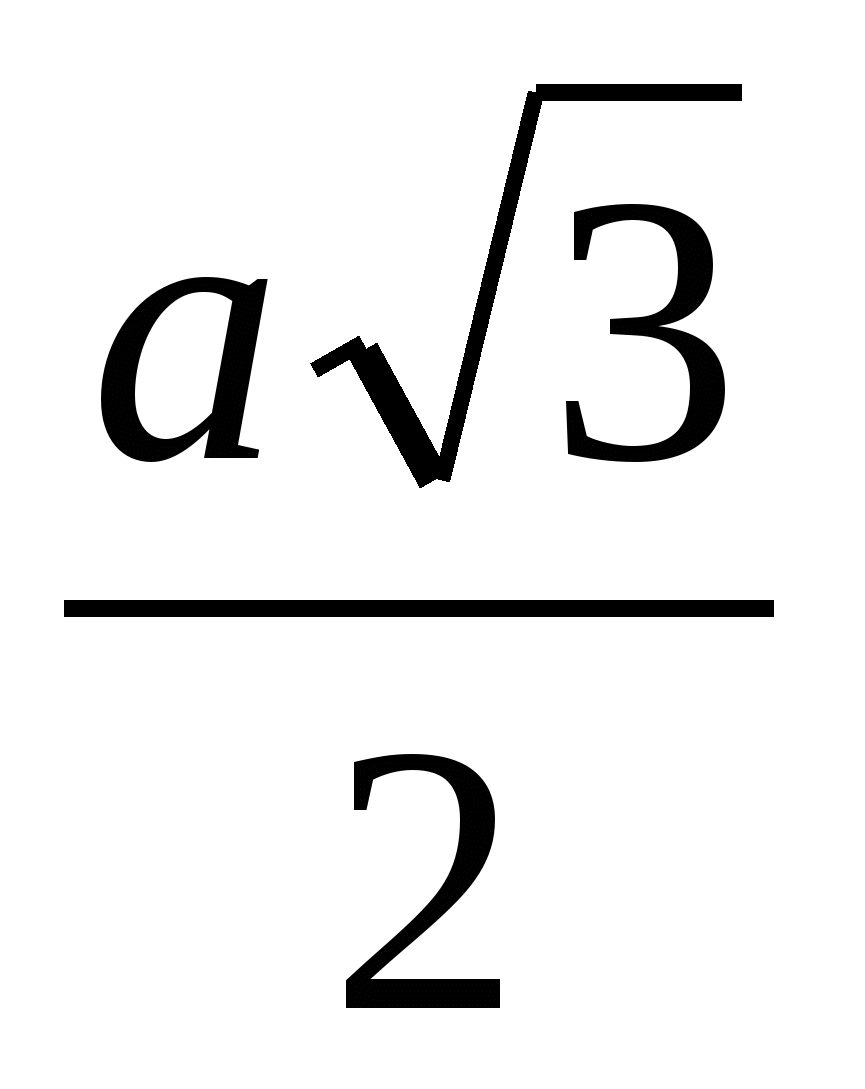
Так как , , , то . Ответ: .

15. Найдите радиусы вписанной и вневписанной окружностей треугольника со сторонами 5, 12, 13.

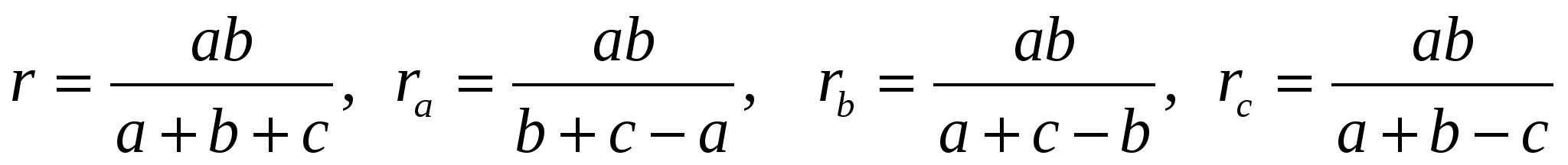
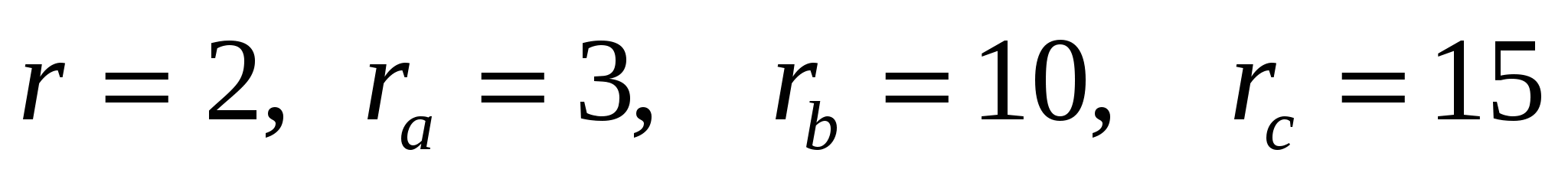
Решение: Если a и b – катеты прямоугольного треугольника, а с – его гипотенуза, то искомые радиусы будут равны: . Таким образом . По-другому:

a — r Ответ:

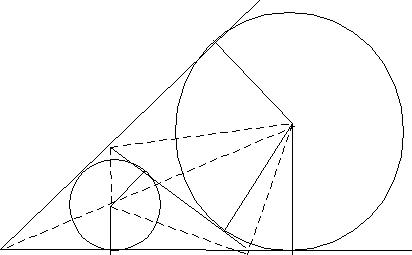
16. В треугольнике PQR величина угла QRP равна 60º. Найдите расстояние между точками касания со стороной QR окружности радиуса 2, вписанной в треугольник, и окружности радиуса 3, касающейся продолжений сторон PQ и PR .

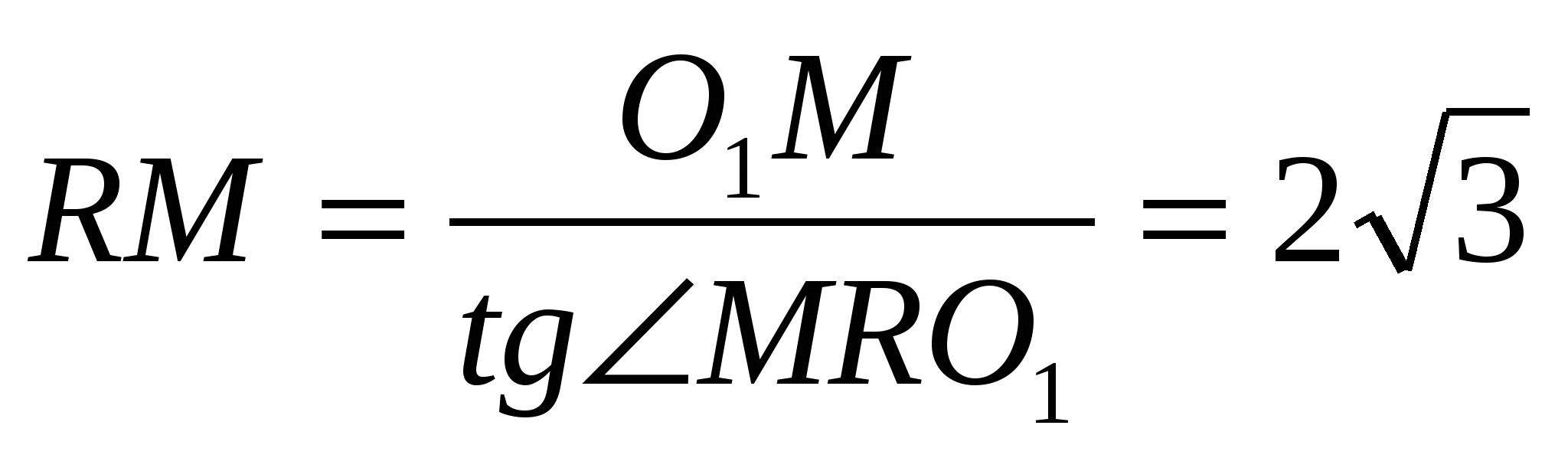
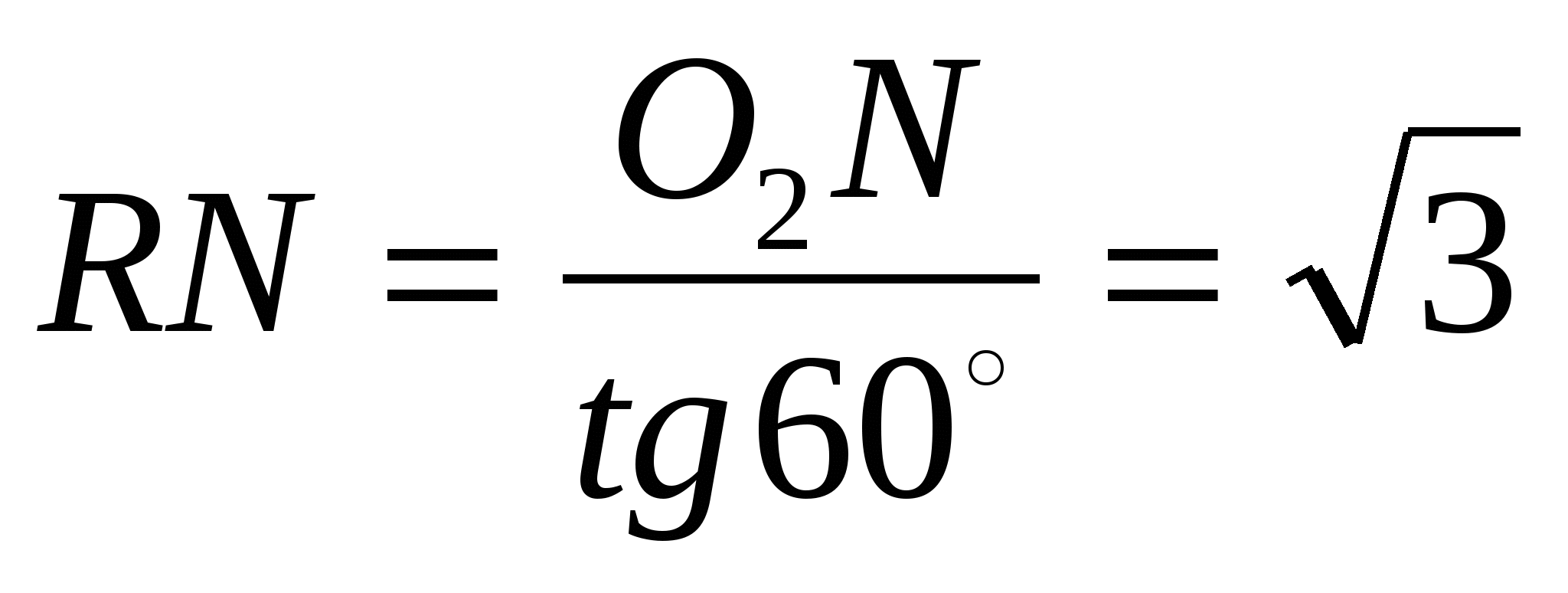
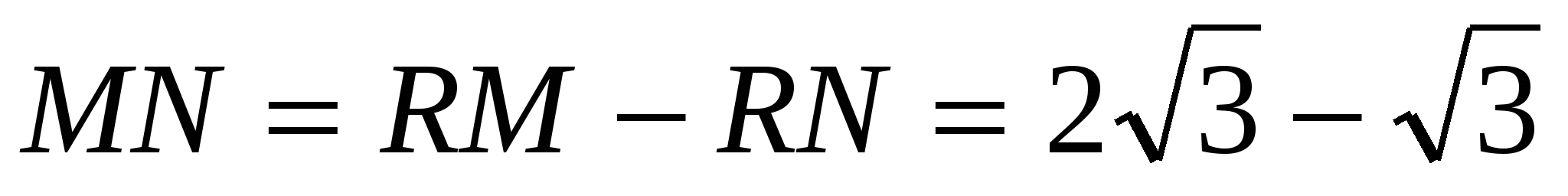
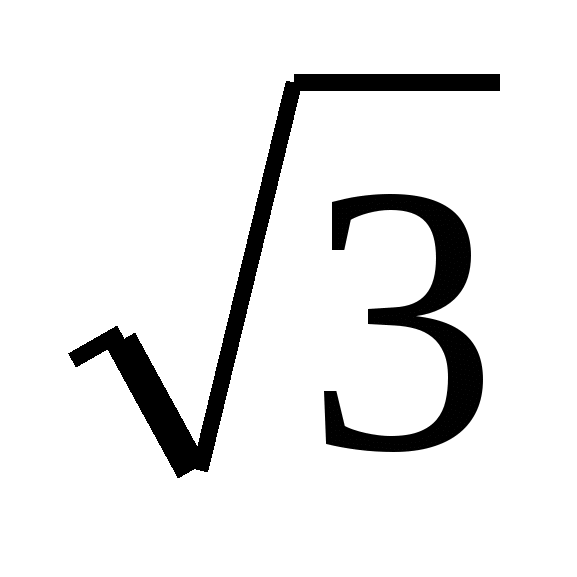
Пусть О₁ и О₂ – центры окружностей радиусов 2 и 3 соответственно, M и N – точки касания окружностей со стороной RQ . Тогда ,. Поэтому. Ответ: .

19. В треугольнике ABC с периметром 2р величина острого угла BAC равна α. Окружность с центром в точке О касается стороны ВС и продолжения сторон АВ и АС в точках K , L и M соответственно. Точка D лежит внутри отрезка АК, AD = а. Найдите площадь треугольника DOK .

Решение:

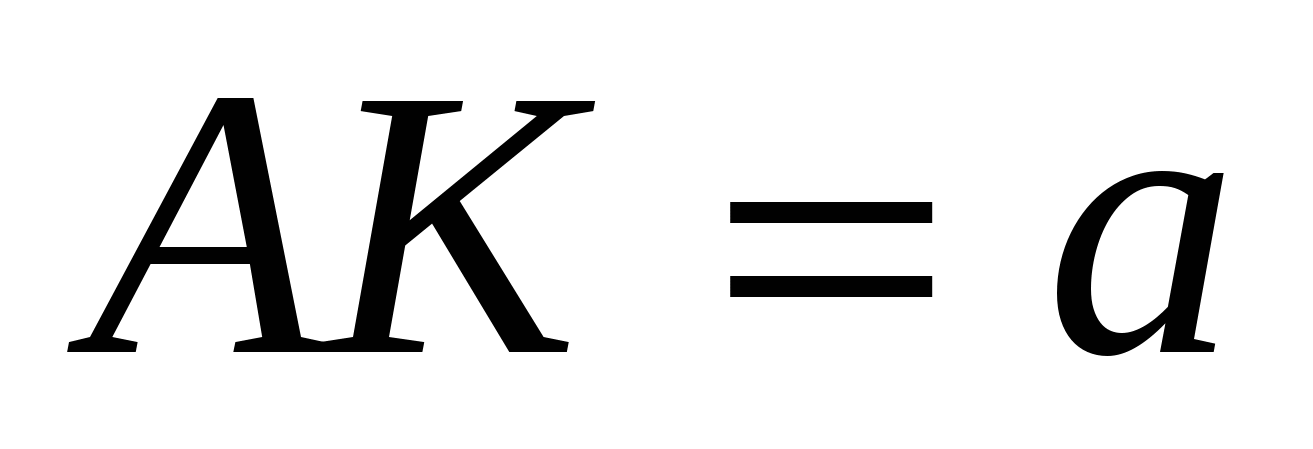
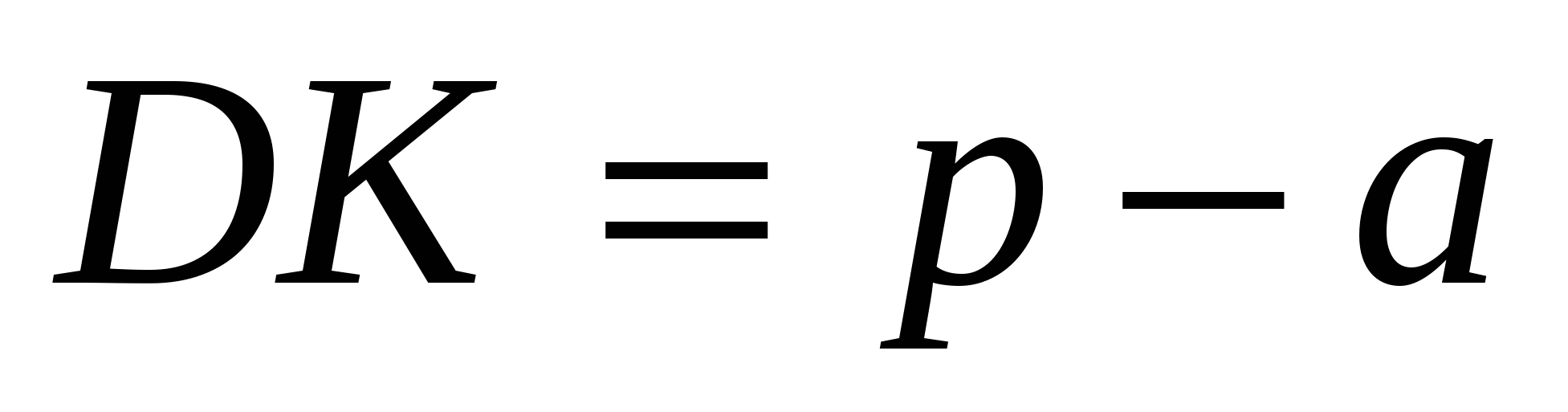
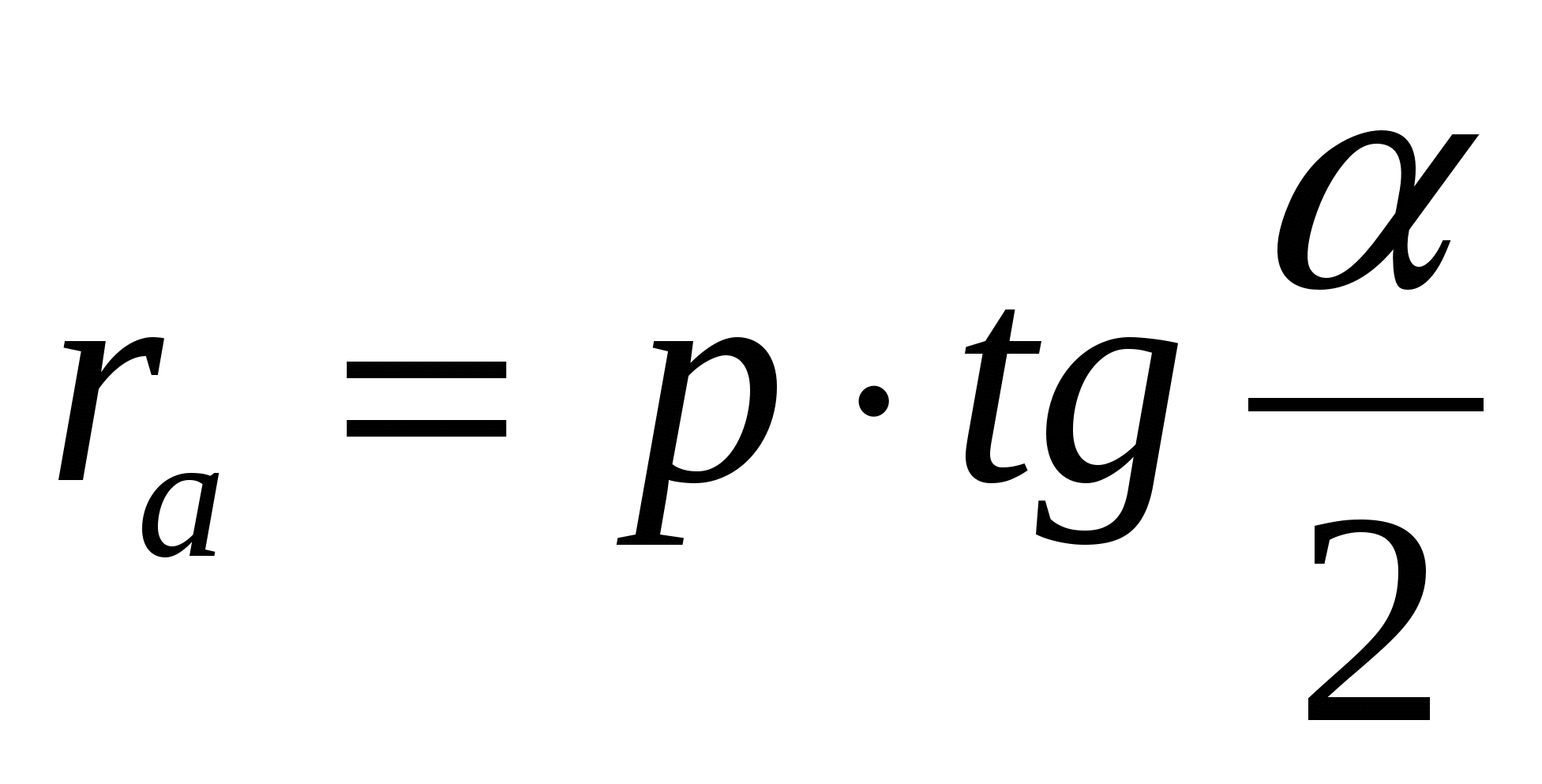
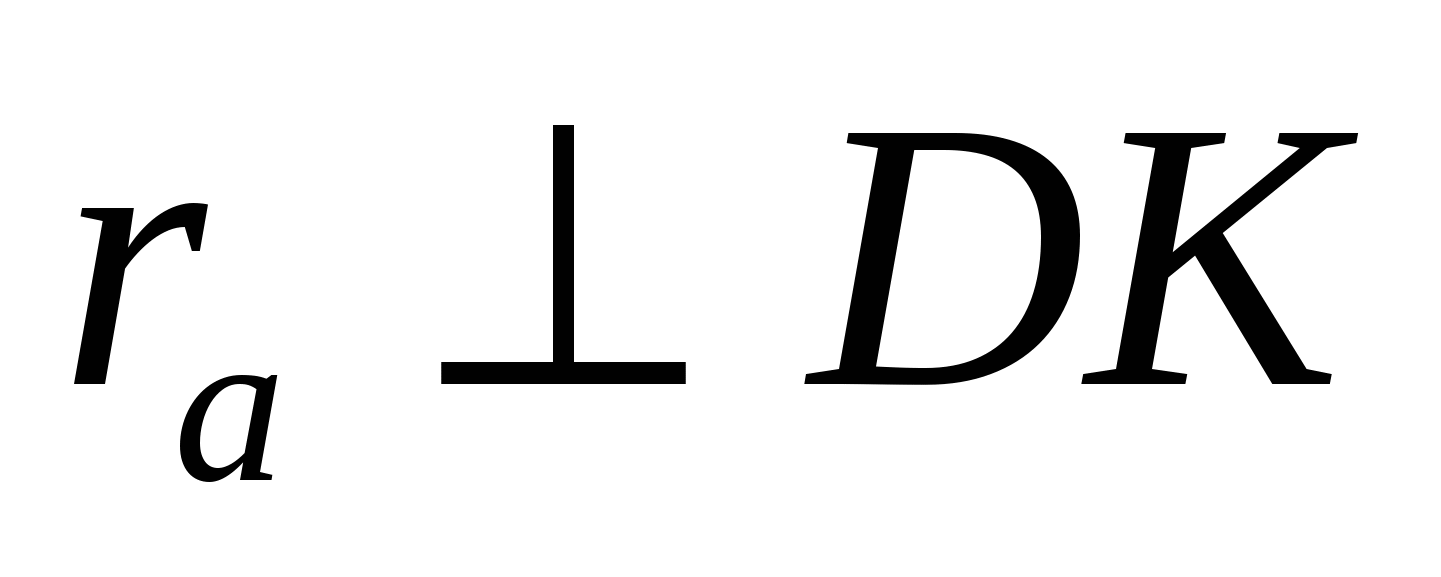
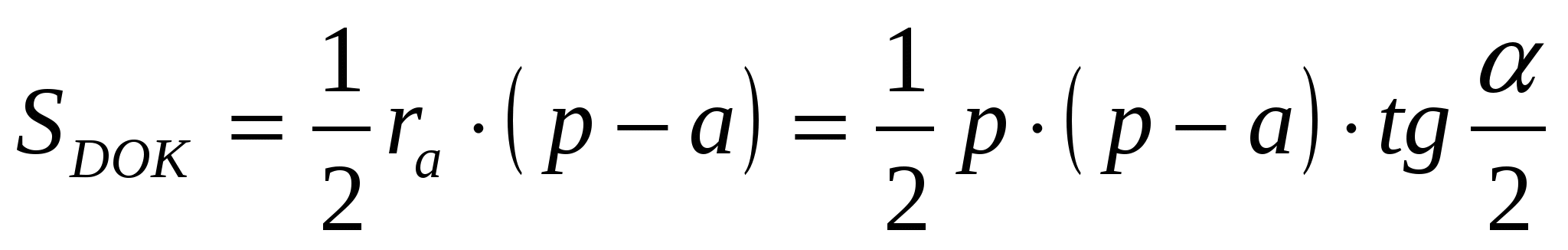
A D B K По теореме 2:, , , так как . Отсюда следует, что .

Ответ: .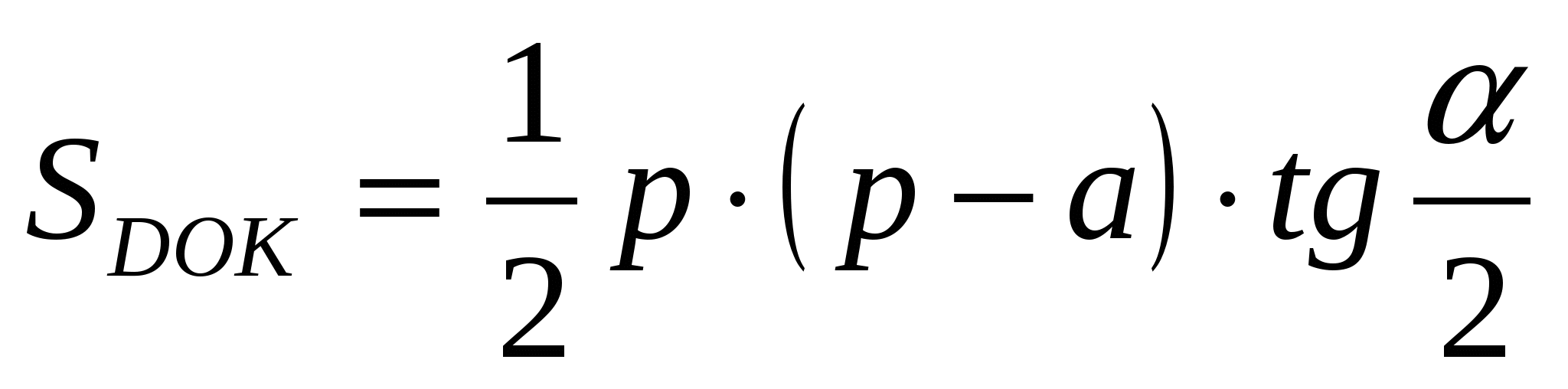

Гнеденко Б.В. Энциклопедический словарь юного математика. М.: «Педагогика», 1989.

Н.Ф. Шарыгин, В.И. Голубев. Факультативный курс по математике: Решение задач. Учеб пособие для 11 кл. сред. шк. – М.: Просвещение, 1991, с. 138-140.

Андреев П.П., Шувалова Э.З. Геометрия.

Прасолов В.В. Задачи по планиметрии. Ч. I М.: Наука, 1986.

Никольская И.Л. Факультативный курс по математике: учебн. Пособие для 7-9 классов ср. школы. — М.: Просвещение, 1991, с.88-91.

Фетисов А.М. Геометрия: учебн. Пособие по программе старших классов. М.: Издательство Академии педагогических наук РСФСР, 1963, 20-21.

Березин В.И. и др. Сборник задач для факультативных и внеклассных занятий по математике. Книга для учителя. — М.: Просвещение, 1985.

Атанасян Л.С., Бутузов В.Ф.. С.Б. Кадомцев, Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы, 9 издание. — М.: Просвещение, 2000.

Энциклопедия для детей т.11. Математика/Глав.ред. М.Д. Аксенова.-М.: Аванта+, 2000.-с. 283

М.Г. Гохидзе «Вневписанная окружность», «Математика в школе», №3, 1989. с. 59

М.Г. Гохидзе «О вневписанной окружности в задачах по стереометрии», «Математика в школе», №5, 1987. с. 54.

«О свойствах центра вневписанной окружности», «Квант», №2, 2001, стр.38.

«Биссектрисы вписанной и вневписанной окружности треугольника», «Квант», №7, 1987.

Моденов П.С. Сборник задач по специальному курсу элементарной математики.- М.: советская наука, 1957.

Васильев Н.Б. и др. Заочные математические олимпиады. – М.: Наука. Главная редакция физико-математической литературы, 1981.

📽️ Видео

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Построить описанную окружность (Задача 1)Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Это будет на ЕГЭ 2020 по математике. Вписанная и вневписанная окружности.Скачать

ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия-7 Окружность и прямая Эйлера, точки ФейербахаСкачать

Центр описанной окружности.Скачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

6.31.1. Планиметрия. Гордин Р.К.Скачать

Точка O центр окружности описанной около остроугольного треугольникаСкачать