Точка касания двух окружностей равноудалена от центров окружностей

Какое из следующих утверждений верно?

1) Точка касания двух окружностей равноудалена от центров этих окружностей.

2) В параллелограмме есть два равных угла.

3) Площадь прямоугольного треугольника равна произведению длин его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Точка касания двух окружностей равноудалена от центров этих окружностей» — неверно: точка касания двух окружностей удалена от центра на величину радиуса каждой окружности.

2) «В параллелограмме есть два равных угла» — верно, в параллелограмме противоположные углы равны.

3) «Площадь прямоугольного треугольника равна произведению длин его катетов» — неверно: площадь прямоугольного треугольника равна половине произведения длин его катетов.

Видео:Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать

Какое из следующих утверждений верно?

Математика | 1 — 4 классы

Какое из следующих утверждений верно?

1)Точка пересечения двух окружностей равноудалена от центров этих окружностей.

2)В параллелограмме есть два равных угла.

3)Площадь прямоугольного треугольника равна произведению длин его катетов.

1)Точка пересечения двух окружностей равноудалена от центров этих окружностей — неверно.

Точка находится на расстояниях, равных радиусам каждой окружности.

Если радиусы различны, то и расстояния различны.

2)В параллелограмме есть два равных угла — верно.

Противоположные углы параллелограмма равны.

3)Площадь прямоугольного треугольника равна произведению длин его катетов — неверно.

Площадь прямоугольного треугольника равна ПОЛОВИНЕ произведения длин его катетов.

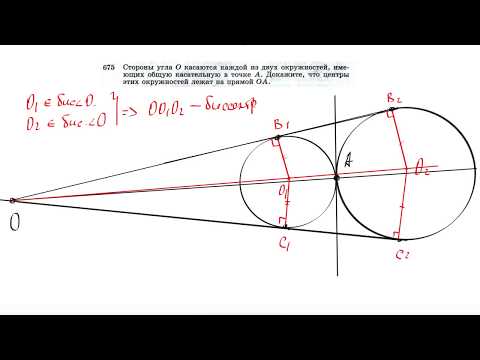
Видео:№675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать

Какое из следующих утверждений верно?

Какое из следующих утверждений верно?

1) В параллелограмме есть два равных угла.

2) Любая биссектриса равнобедренного треугольника является его медианой.

3) Площадь прямоугольного треугольника равна произведению длин его катетов.

Видео:Точка пересечения двух окружностей равноудалена ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Какие из данных утверждений верны?

Какие из данных утверждений верны?

1) Вокруг любого треугольника можно описать окружность.

2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

3) Площадь трапеции равна произведению средней линии на высоту.

4) В тупоугольном треугольнике все углы тупые.

5) В любом параллелограмме диагонали точкой пересечения делятся пополам.

6) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.

Видео:Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Центр окружности, касающейся катетов прямоугольного треугольника, лежит нагипотенузе?

Центр окружности, касающейся катетов прямоугольного треугольника, лежит нагипотенузе.

Найти радиус окружности, если он в 7 раз меньше суммы катетов, а

площадь треугольника равна 56.

Видео:Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1. Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

2. Площадь трапеции равна произведению основания трапеции на высоту.

3. Треугольника со сторонами 1, 2, 4 не существует.

Видео:1 2 4 сопряжение окружностейСкачать

Какое из следующих утверждений верно?

Какое из следующих утверждений верно?

1)смежные углы равны, 2)через любую точку лежащую вне окружности, можно провести две касательные к этой окружности, 3)площадь параллелограмма равна половине произведения его диагоналей.

Видео:ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1)расстояние от точки, лежащей на окружности, до центра этой окружности равно радиусу этой окружности.

2)средняя линия традиции равна сумме ее оснований.

3)площадь пароллелограмма равна половине произведения его диогоналий.

Видео:Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

Какое из утверждений верно?

Какое из утверждений верно?

1) Высота всегда образует с прямой, содержащей одну из сторон треугольника, равные углы.

2) В прямоугольном треугольнике высота не совпадает с одной из его сторон.

3) Точка пересечения высот произвольного треугольника – центр окружности, описанной около этого треугольника.

4) Высота всегда делит треугольник на два треугольника равной площади.

Видео:Задачи региона ВсОШ на степень точкиСкачать

Какие из следующих утверждений верны1) смежные углы равны2) площадь квадрата равна произведению его двух смежных сторон3) длинна гипотенузы прямоугольного треугольника меньше суммы длин его катетов?

Какие из следующих утверждений верны

1) смежные углы равны

2) площадь квадрата равна произведению его двух смежных сторон

3) длинна гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

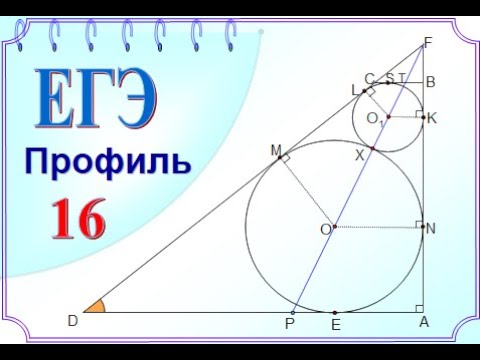
Видео:ЕГЭ Задание 16 Две касающиеся окружностиСкачать

Какое из следующих утверждений верно?

Какое из следующих утверждений верно?

1) Всегда один из двух смежных углов острый а другой тупой 2) площадь квадрата равна произведению двух его смежных сторон 3) все хорды одной окружности равны между собой.

Видео:Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Какое из следующих утверждений верно?

Какое из следующих утверждений верно?

1. Любой параллелограмм можно вписать в окружность.

2. Касательная к окружности параллельна радиусу, проведённому в точку касания.

3. Сумма острых углов прямоугольного треугольника равна 90 градусам.

На этой странице сайта вы найдете ответы на вопрос Какое из следующих утверждений верно?, относящийся к категории Математика. Сложность вопроса соответствует базовым знаниям учеников 1 — 4 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

1) 180 : 6 = 30 м провода использовали в спортзале 2) 180 — 30 = 150 м израсходовали на лампы 3) 150 : 15 = 10 м ушло на одну лампу Ответ : 10м.

180 / 6 = 30 метров 180 — 30 = 150 метров осталось 150 / 15 = 10 метров на 1 лампу.

Длина прямоугольника равна 10 см, ширина 7см, высота 5 см. Найдите объем прямоугольника. 1) 10 * 7 * 5 = 350см2 — обхем прямоугол ника Ртвет : 350см2.

3) Используем свойства степеней. (((16 ^ (2 / 3)) * 25 ^ (2 / 3)) / ((4 ^ ( — 2 / 3)) * (125 ^ (1 / 9)))) ^ ( — 1) = = (((4 ^ (4 / 3)) * 5 ^ (4 / 3)) / ((4 ^ ( — 2 / 3)) * (5 ^ (3 / 9)))) ^ ( — 1) = = (((4 ^ (4 / 3)) * 5 ^ (4 / 3)) * ((4 ^ (2 / 3)) ..

24 : 3 = 1 * 8 вот и ответ легко))))))))))).

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Точка касания двух окружностей равноудалена от центров окружностей

Задание 20. Какое из следующих утверждений верно?

1) Точка пересечения двух окружностей равноудалена от центров этих окружностей.

2) В параллелограмме есть два равных угла.

3) Площадь прямоугольного треугольника равна произведению длин его катетов.

1) Нет, если окружности имеют разные радиусы, то точка пересечения будет удалена на величины этих радиусов.

2) Да, в параллелограмме противоположные углы равны.

3) Нет, площадь прямоугольного треугольника равна половине произведения длин его катетов.

🎬 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

Взаимное расположение двух окружностей.6 классСкачать

Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать

ЕГЭ Задание 16 Внешнее касание трёх окружностейСкачать

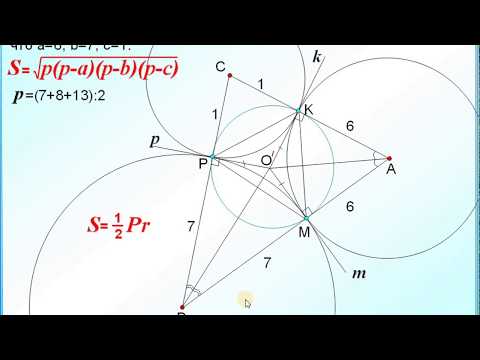
Тема 26. Взаимное расположение окружностейСкачать

Касание окружностей | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Разбор задания 13 ОГЭ по математикеСкачать