Tgx меньше 1 на окружности (6 видео) | Курс школьной геометрии

Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Содержание

Узнать ещё
a»>tgx>a
Функция y = tg x, её свойства и график
п.1. Развертка тангенса движения точки по числовой окружности в функцию от угла
п.2. Свойства функции y=tgx⁡
п.3. Примеры
💡 Видео

Видео:Решить неравенство tg xСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Как решать тригонометрические неравенства?Скачать

a»>tgx>a

Рассмотрим решение тригонометрических неравенств вида tgx>a и tgx

Для решения нам потребуется чертеж единичной окружности и линия тангенсов . Радиус единичной окружности равен 1, поэтому, откладывая на линии тангенсов отрезки, длина которых равна радиусу, получаем соответственно точки, в которых тангенс равен 1, 2, 3 и т.д., а вниз — -1,-2,-3 и т.д.

1) tgx>a

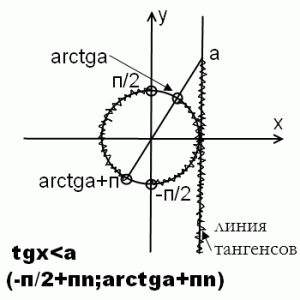
На линии тангенсов значениям тангенсов, большим a, соответствует часть, расположенная выше точки а. Заштриховываем соответствующий луч. Теперь проводим прямую через точку О — начало отсчета- и точку а на линии тангенсов. Она пересекает окружность в точке arctg a. Соответственно, на окружности решению неравенства tgx>a соответствует дуга от точки arctg a до п/2. Чтобы учесть все решения (а их с учетом периодичности тангенса — бесконечное множество), к каждому концу интервала прибавляем пn, где n — целое число (n принадлежит Z).

Для решения неравенства tgx>a вполне достаточно полуокружности от -п/2 до п/2. Но если требуется найти, к примеру, решение системы неравенств с тангенсом и синусом, то нужна вся окружность.

Если неравенство нестрогое, точку с arctg a включаем в ответ (на рисунке ее заштриховываем, в ответ записываем с квадратной скобкой). Точка п/2 в ответ никогда не включается, поскольку не входит в область определения тангенса (точка выколотая, скобка круглая).

2) tgx>-a

Чтобы решить неравенство tgx>-a, рассуждаем так же как и для неравенства tgx>a. Поскольку arctg (-a)=-arctg a, только этим и отличается ответ.

В этом случае решению неравенства tgx

4) tgx Светлана Иванова, 17 Окт 2012

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Функция y = tg x, её свойства и график

п.1. Развертка тангенса движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности на вертикальной касательной, проведенной через точку (1;0), отображаются значения тангенсов соответствующих углов (см. §3 данного справочника).

Рассмотрим, как изменяется тангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=tgx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x тангенцоидой .
Часть тангенцоиды c (-fracpi2lt xlt fracpi2) называют главной ветвью тангенцоиды .

п.2. Свойства функции y=tgx⁡

1. Область определения (xnefracpi2+pi k) — множество действительных чисел, кроме точек, в которых (cosx=0) .

2. Функция не ограничена сверху и снизу. Область значений (yinmathbb)

3. Функция нечётная $$ tg(-x)=-tgx $$

4. Функция периодическая с периодом π $$ tg(x+pi k)=tgx $$

5. Функция стремится к (+infty) при приближении слева к точкам (x=fracpi2+pi k) .
Приближение к точке a слева записывается как (xrightarrow a-0) $$ lim_ tgx=+infty $$ Функция стремится к (-infty) при приближении справа к точкам (x=fracpi2+pi k) .
Приближение к точке a справа записывается как (xrightarrow a+0) $$ lim_ tgx=-infty $$ Нули функции (y_=0) достигаются в точках (x_0=pi k)

6. Функция возрастает на всей области определения.

7. Функция имеет разрывы в точках (x=fracpi2+pi k) , через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами (left(-fracpi2+pi k; fracpi2+pi kright)) функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=tgx на заданном промежутке:

a) (left[frac; fracright)) $$ y_=tgleft(fracright)=-sqrt, y_=lim_<xrightarrowfrac-0>tgx=+infty $$ б) (left(frac; piright]) $$ y_=lim_<xrightarrowfrac+0>tgx=-infty, y_=tg(pi)=0 $$ в) (left[frac; fracright]) $$ y_=tgleft(fracright)=-1, y_=tgleft(fracright)=frac<sqrt> $$

Пример 2. Решите уравнение:
a) (tgx=-sqrt)
Бесконечное множество решений: (x=frac+pi k, kinmathbb)

б) (tgleft(x-fracpi2right)=0)
(x-fracpi2=pi k)
Бесконечное множество решений: (x=frac+pi k, kinmathbb)

в) (tg(2x)=1)
(2x=fracpi4+pi k)
Бесконечное множество решений: (x=frac+frac, kinmathbb)

Пример 3. Определите чётность функции: a) (y(x)=4tgx+5sinx)
$$ y(-x)=4tg(-x)+5sin(-x)=-4tgx-5sinx=-(4tgx+5sinx)=-y(x) $$ Функция нечётная.

б) (y(x)=tgx-2cosx)
$$ y(-x)=tg(-x)-2cos(-x)=-tgx-2cosx=-(tgx+2cosx)ne left[ begin -y(x)\ y(x) end right. $$ Функция ни чётная, ни нечётная.

в) (y(x)=tg^2x+cos5x)
$$ y(-x)=tg^2(-x)+cos(-5x)=(-tgx)^2+cos5x=tg^2x+cos5x)=y(x) $$ Функция чётная.

г) (y(x)=x^2-tgx)
$$ y(-x)=(-x)^2-tg(-x)=x^2+tgxne left[ begin -y(x)\ y(x) end right. $$ Функция ни чётная, ни нечётная.

Пример 4. Если (tg(7pi-x)=frac34), то чему равны (tgx, ctgx)?
Т.к. период тангенса равен π, получаем: begin tg(7pi-x)=tg(-x)=-tgx=frac34Rightarrow tgx=-frac34\ ctgx=frac=-frac43 end Ответ: (-frac34, -frac43)