Tg 1 на окружности tg1 единичной (7 видео) | Курс школьной геометрии

Узнать ещё

Знание — сила. Познавательная информация

Содержание

Тангенс 1, tg 2, tg 3
Значения тангенса и котангенса на тригонометрическом круге
Алгебра
Синус и косинус угла на единичной окружности
💥 Видео

Видео:Тригонометрическая окружность. Как выучить?Скачать

Тангенс 1, tg 2, tg 3

Когда требуется найти тангенс 1, tg 2, tg 3, tg 4, tg 6, помогут единичная окружность и линия тангенсов.

Для начала отметим на единичной окружности углы в 1, 2, 3, 4, 5 и 6 радиан. Это можно сделать тремя способами.

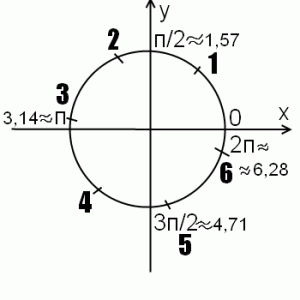
1) 1 радиан — это приблизительно 57 градусов. Соответственно, через каждые 57 градусов отмечаем: 1 радиан, 2, 3…

2) 1 радиан — это угол, длина дуги которого равна радиусу окружности. В этом случае каждую следующую отметку ставим, откладывая приблизительно дугу длиной в радиус.

3) если вспомнить, что п — это приближенно 3,14, и рассчитать п/2, 3п/2, 2п, а 1,2, 3,4,5 и 6 радиан — ориентируясь на эти значения.

Получаем приблизительно такой чертеж:

Если нужно сравнить, например, tg1 и tg2, этого чертежа вполне достаточно. 1 радиан — угол 1й четверти, где тангенс положителен, а 2 радиана — угол 2й четверти, где тангенс отрицателен (см. как запомнить знаки тангенса ). Поэтому tg1 > tg2.

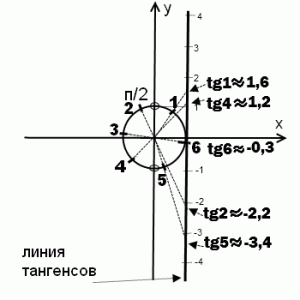
Когда требуется сравнить тангенсы одного знака, например, tg 5 и tg 6, единичной окружности недостаточно. Найти значения tg1, tg2, tg3, tg4, tg6 можно также с помощью линии тангенсов.

Линия тангенсов — это касательная к единичной окружности в точке (1;0). То есть линия тангенсов — это прямая x=1.

Если через точку О — начало отсчета- и отмеченный на единичной окружности угол в 1 радиан провести луч, то он пересечет линию тангенсов в точке, которая показывает значения tg 1. Поскольку окружность единичная, то значения 2,3,4 и т.д. получаем, откладывая на линии тангенсов длину радиуса. Соответственно, tg 1 получаем где-то посредине между 1 и 2, чуть ближе к 2. Аналогично на линии тангенсов определяем, чему равен тангенс 2, тангенс 3, тангенс 4, тангенс 5 и тангенс 6. Отсюда делаем вывод: tg5 tg5, tg4 Светлана Иванова, 14 Окт 2012

Видео:Тригонометрическая окружность tg x и ctg xСкачать

Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть