Тест касательная к окружности ответы

Касательная к окружности

Сколько точек пересечения имеет окружность и касательная?

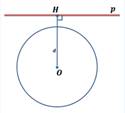
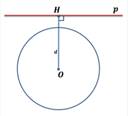
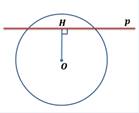
Укажите рисунок, на котором изображена касательная к окружности.

Выберите один из 3 вариантов ответа:

1) 2) 3)

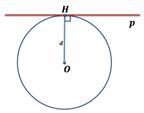
Составьте верные соответствия между соотношением расстояния от центра окружности до прямой ( d ) и радиусам окружности ( r ):

Укажите соответствие для всех 3 вариантов ответа:

1) прямая и окружность имеют две общие точки

2) прямая и окружность не имеют общих точек

3) прямая и окружность имеют одну общую точку

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Определить взаимное расположение прямой и окружности, если:

d = 2014, r = 2015

Выберите один из 3 вариантов ответа:

1) прямаяи окружность не пересекаются

2) прямая является касательной к окружности

3) прямая является секущей к окружности

Какой угол образует касательная к окружности с радиусом, проведенным к точке касания?

Выберите один из 4 вариантов ответа:

Выберите верные утверждения:

Выберите несколько из 5 вариантов ответа:

1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

2) Касательная пересекает окружность в двух точках.

3) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

4) Отрезки касательных к окружности, проведенные из одной точки параллельны.

5) Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

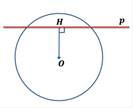
Укажите рисунок, на котором изображена секущая к окружности.

Выберите один из 3 вариантов ответа:

1) 2) 3)

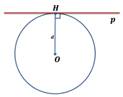
Сколько точек пересечения имеет окружность и секущая?

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Тест по теме «Касательная к окружности».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Тест по теме «Касательная к окружности» .

Задания по готовым чертежам (рисунок) по теме «Касательная к окружности»:

Так как к этому моменту ученики уже знакомы с понятием секущая и определились с понятием касательная, как прямой, имеющей с окружностью одну общую точку , то возможны следующие вопросы:

1. На каких рисунках МК является секущей?

2. На каких рисунках прямая МК — касательная к окружности?

3. Пусть вам дана окружность и точка на ней. Можно ли построить 2 касательные к окружности, проходящие через данную точку?

Построить свой ответ.

4. Через каждую ли точку окружности можно провести касательную?

Построить свой ответ.

Задания 1-3 характеризуют второй уровень овладения действиями рассматриваемого, причем задания 1 , 2 — направлены на отработку действия распознавания объектов, принадлежащих объему понятия «касательная», а 3 на выведение следствий, четвертое сформулировано для учащихся, находящихся на третьем и четвертом уровнях овладения. Задания 3 и 4 заставляют учащихся размышлять, самостоятельно делать выводы, проверять при помощи построений их правильность, а, следовательно, показывают, как при помощи тестирования реализуется воспитательная функция обучения.

Краткое описание документа:

Тестирование может включать в себя задания по всем темам курса, это позволяет выявить знания учащегося по всему курсу. При помощи тестирования можно установить уровень знаний учащегося по предмету в целом и по отдельным его разделам. Тестирование ставит всех учащихся в равные условия, используя единую процедуру и единые критерии оценки.

Предлагается тест по теме «Касательная к окружности».

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 936 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 317 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 695 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 478 623 материала в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

69. Касательная к окружности

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Дистанционные курсы для педагогов

Другие материалы

• 08.08.2019
• 527

• 08.08.2019
• 178

• 08.08.2019
• 202

• 08.08.2019
• 414

• 14.05.2019
• 259

• 04.03.2019
• 163

• 27.01.2019
• 2238

• 27.01.2019
• 886

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 09.08.2019 1750 —> —> —> —>
• DOCX 33.8 кбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Малькова Людмила Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На проекте: 7 лет и 10 месяцев
• Подписчики: 0
• Всего просмотров: 7180
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Якутске все классы, кроме девятых и одиннадцатых, перейдут на удаленку

Время чтения: 1 минута

Стартовал региональный этап Всероссийской олимпиады школьников

Время чтения: 2 минуты

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В местах сдачи ЕГЭ будут применены антиковидные меры

Время чтения: 1 минута

В России ежегодно будут обучать плаванию не менее 500 тыс. детей

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Касательная к окружности | Геометрия 7-9 класс #69 | ИнфоурокСкачать

Тест касательная к окружности ответы

Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.

Найдем отрезок DO: DO = OB − BD = 5 − 1 = 4. Так как OB перпендикулярен AC, треугольник AOD — прямоугольный. По теореме Пифагора имеем: . Треугольник AOC — равнобедренный так как AO = OC = r, тогда AD = DC. Таким образом, AC = AD·2 = 6.

Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.

Проведем радиусы OA и OB. Так как по условию задачи хорда AB равна радиусу, то треугольник AOB — равносторонний, следовательно, все его углы равны 60°. Угол AOB — центральный и равен 60° Угол ACB — вписанный и опирается на ту же дугу, что и угол AOB. Таким образом,

К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB. Из теоремы Пифагора:

В треугольнике ABC угол C равен 90°, AC = 30 , BC = Найдите радиус окружности, описанной около этого треугольника.

Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы. По теореме Пифагора имеем:

Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.

Проведём построение и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и HOB, они прямоугольные, OH — общая, AO и OB равны как радиусы окружности, следовательно, эти треугольники равны, откуда По теореме Пифагора найдём радиус окружности:

Диаметр равен двум радиусам, следовательно,

🔥 Видео

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ в точке ЗАДАЧИ 8 классСкачать

#59. Олимпиадная задача о касательной к окружности!Скачать

Секущая и касательная. 9 класс.Скачать

Решение задач Касательная к окружностиСкачать

ЕГЭ ОГЭ КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ. ГЕОМЕТРИЯСкачать

Секретная теорема из учебника геометрииСкачать

ОГЭ математика. Задание 16. Окружность. Касательная.Скачать

Построение касательной к окружностиСкачать

Геометрия 5. Касательная к окружности.Скачать

ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Касательная к окружностиСкачать

Геометрия 8 класс: Решение задач на касательную к окружностиСкачать

КАСАТЕЛЬНАЯ к ОКРУЖНОСТИ 8 класс геометрия АтанасянСкачать