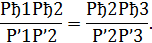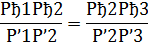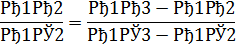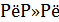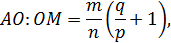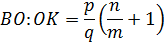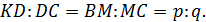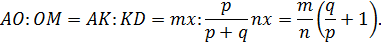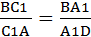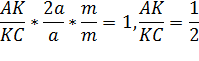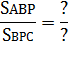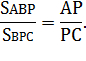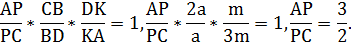Теорема пропорциональных отрезков треугольника (7 видео)

Подобие треугольников и пропорциональные отрезки

Теорема 1:

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство:

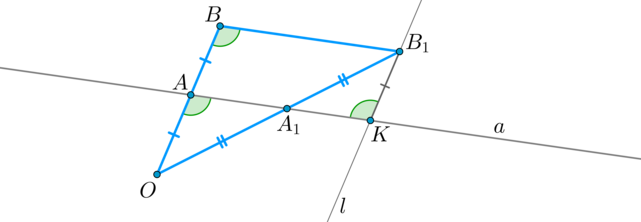
Докажем сначала лемму: Если в (triangle OBB_1) через середину (A) стороны (OB) проведена прямая (aparallel BB_1) , то она пересечет сторону (OB_1) также в середине.

Через точку (B_1) проведем (lparallel OB) . Пусть (lcap a=K) . Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle A_1KB_1=angle ABB_1=angle OAA_1) . Значит, по второму признаку (triangle OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1) . Лемма доказана.

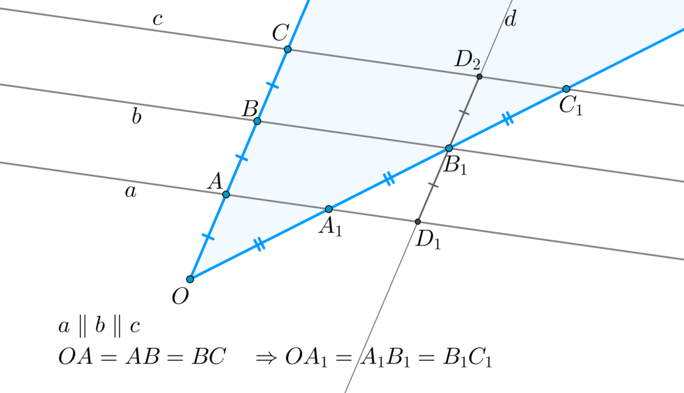
Перейдем к доказательству теоремы. Пусть (OA=AB=BC) , (aparallel bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1) .

Таким образом, по данной лемме (OA_1=A_1B_1) . Докажем, что (A_1B_1=B_1C_1) . Проведем через точку (B_1) прямую (dparallel OC) , причем пусть (dcap a=D_1, dcap c=D_2) . Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2) . Значит, по первому признаку (triangle A_1B_1D_1=triangle C_1B_1D_2 Rightarrow A_1B_1=B_1C_1) .

Теорема Фалеса:

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство:

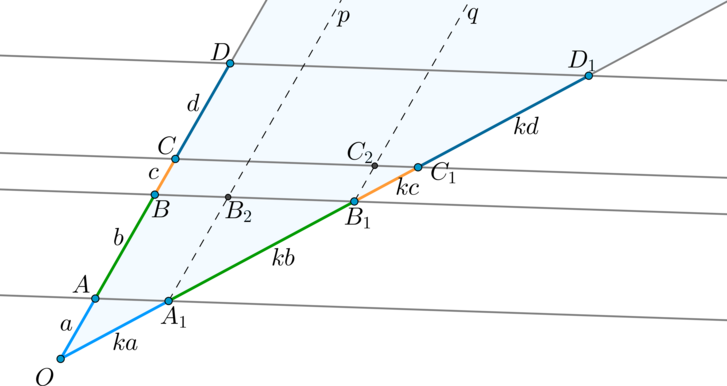
Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d) . Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно.

Проведем через точку (A_1) прямую (pparallel OD) ( (ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2) ). Тогда (triangle OAA_1 sim triangle A_1B_1B_2) по двум углам. Следовательно, (dfrac=dfrac Rightarrow A_1B_1=kb) .

Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.

Наиболее часто встречающиеся подобия треугольников:

Теорема 2.

Средняя линия треугольника отсекает от него подобный ему треугольник.

Доказательство:

Т.к. средняя линия — это отрезок, соединяющий середины двух сторон, то (dfrac =dfrac=2) .

Таким образом, по двум пропорциональным сторонам и углу между ними ( (angle B) — общий) (triangle A_1BC_1 sim triangle ABC) .

Теорема 3.

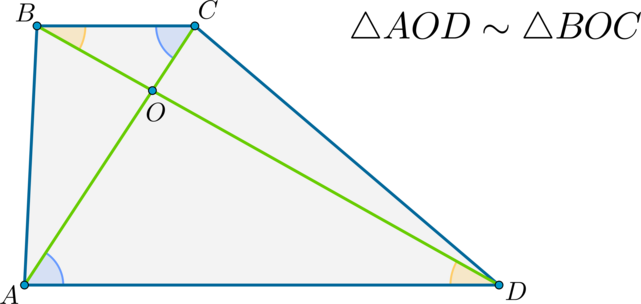
Треугольники, образованные диагоналями трапеции и основаниями, подобны.

Доказательство:

Т.к. (ADparallel BC Rightarrow angle OBC=angle ODA) . (angle BOC=angle AOD) как вертикальные. Следовательно, по двум углам (triangle BOCsim triangle AOD) .

Теорема 4.

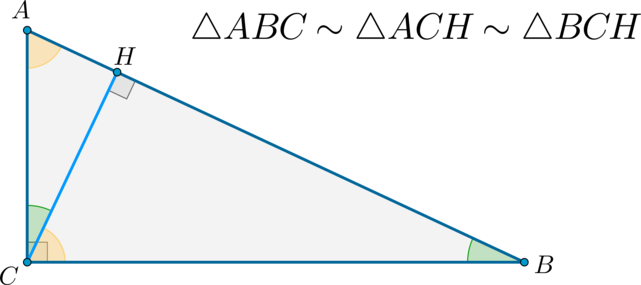
Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.

Доказательство:

Обозначим (angle ACH=alpha, angle BCH=beta) , т.е. (alpha+beta=90^circ) . Тогда (angle CAH=90^circ-alpha=beta, angle CBH=90^circ-beta=alpha) .

Следовательно, по двум углам (triangle ACHsim triangle BCHsim ABC) .

Теорема 5.

Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.

Эти отрезки также являются биссектрисами углов треугольника, вершинами которого являются основания данных высот.

Доказательство:

1) Рассмотрим четырехугольник (AC_1A_1C) — около него можно описать окружность, т.к. (angle AC_1C=angle AA_1C) . Таким образом, (angle CAA_1=angle CC_1A_1=x) , т.к. опираются на одну и ту же хорду (A_1C) . Таким образом (angle ACA_1=90^circ-x, angle BC_1A_1=90^circ-x Rightarrow angle ACA_1=angle BC_1A_1) .

Значит, по двум углам (triangle A_1BC_1sim triangle ABC) ( (angle B) — общий).

Аналогично доказывается, что (triangle AB_1C_1sim triangle ABC, triangle A_1B_1Csim triangle ABC) .

2) Докажем, что (AA_1, BB_1, CC_1) – биссектрисы углов (A_1, B_1, C_1) в треугольнике (A_1B_1C_1) соответственно.

Обозначим (angle BC_1A_1=angle B_1C_1A=alpha) . Тогда (angle A_1C_1C=90^circ -alpha=angle B_1C_1C) . Значит, (CC_1) – биссектриса угла (C_1) .

Аналогично доказывается про (AA_1) и (BB_1) .

Теорема 6.

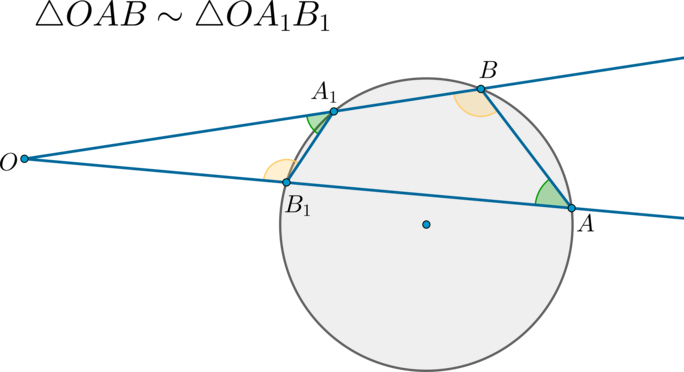
Если к окружности из одной точки вне окружности проведены две секущие, то:

Доказательство:

Четырехугольник (ABA_1B_1) описанный, следовательно, (angle BAB_1+angle BA_1B_1=180^circ Rightarrow angle OA_1B_1=180^circ-angle BA_1B_1=angle BAB_1) .

Таким образом, по двум углам ( (angle O) — общий) (triangle OABsim triangle OA_1B_1) .

Теорема 7.

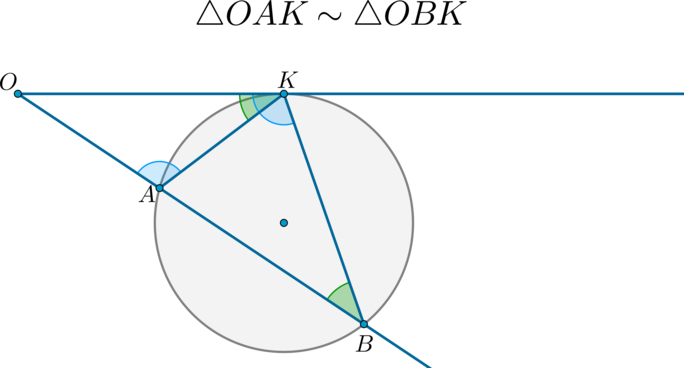
Если к окружности из одной точки проведены касательная и секущая, то:

Доказательство:

Т.к. угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то (angle OKA=frac12 buildrelsmileover=angle KBA) .

Следовательно, по двум углам ( (angle O) — общий) (triangle OKAsim triangle OKB) .

Теорема 8.

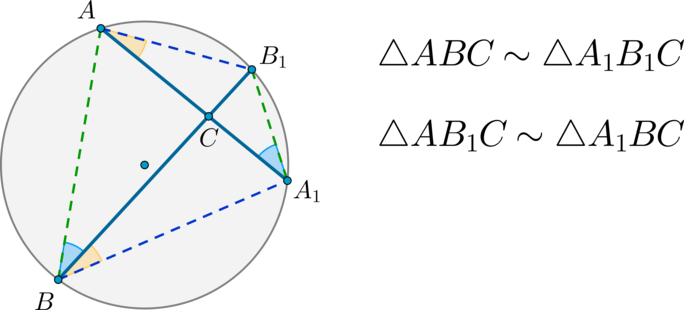
Если в окружности две хорды пересекаются, то:

Доказательство:

(angle A_1AB_1=angle A_1BB_1) , т.к. опираются на одну и ту же дугу. (angle A_1CB=angle B_1CA) , т.к. они вертикальные. Следовательно, по двум углам (triangle A_1BCsim triangle B_1C) .

Аналогично (triangle ABCsim triangle A_1B_1C) .

Видео:Теорема о пропорциональных отрезках Скачать

Теорема о пропорциональных отрезках в треугольнике.

Введение.

Мой реферат посвящен применению подобия к доказательству теорем и решению задач, а именно глубоко изучить обобщение теоремы Фалеса, теоремы Чевы и Менелая, которые не изучаются в школьной программе. Теме подобия, которая проходится в восьмом классе, отведено всего лишь 19 часов, что недостаточно для изучения этой темы более углубленно. В тему подобия входят: определение подобных треугольников, признаки подобия, отношение площадей подобных треугольников, средняя линия треугольника, пропорциональные отрезки и т.д.

Напомню определение подобных треугольников:

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Оказывается, что у подобных треугольников не только отношение сходственных сторон, но и отношение любых других сходственных отрезков равно коэффициенту подобия. Например, отношение сходственных биссектрис AD и A₁D₁, т.е. биссектрис равных углов A и A₁в подобных треугольниках ABC и A₁B₁C₁, равно коэффициенту подобия k, отношение сходственных медиан AM и A₁M₁ равно k и точно так же отношение сходственных высот AH и A₁H₁ равно k.

С помощью данного материала, который изучается в школьной программе, мы можем решать довольно узкий круг задач. При создании своего реферата я собираюсь углубить свои знания по данной теме, что позволит решать более широкий круг задач на пропорциональные отрезки. В этом и заключается актуальность моего реферата.

Одна из теорем – это обобщение теоремы Фалеса. Сама теорема Фалеса проходится в восьмом классе. Но главными теоремами являются теоремы Чевы и Менелая.

Обобщение теоремы Фалеса.

Формулировка:

Параллельные прямые, пересекающие две данные прямые, отсекают на этих прямых пропорциональные отрезки.

=…= .

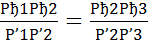
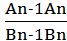
Доказательство:

Докажем, например, что

Рассмотрим два случая:

Случай

Прямые a и b параллельны. Тогда четырехугольники А1А2В2В1 и А2А3В3В2 – параллелограммы. Поэтому А1А2=В1В2 и А2А3=В2В3, откуда следует, что

Случай

Прямые a и b не параллельны. Через точку А1 проведем прямую с, параллельную прямой b. Она пересечет прямые А2В2 и А3В3 в некоторых точках С2 и С3. Треугольники А1А2С2 и А1А3С3подобны по двум углам (угол А1 – общий, углы А1А2С2 и А1А3С3 равны как соответственные при параллельных прямых А2В2 и А3В3 секущей А2А3), поэтому

Отсюда по свойству пропорций получаем:

(1)

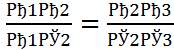
С другой стороны, по доказанному в первом случае имеем А1С2=В1В2, С2С3=В2В3. Заменяя в пропорции (1) А1С2 на В1В2 и С2С3 на В2В3, приходим к равенству

(2)

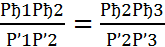
что и требовалось доказать.

Теорема о пропорциональных отрезках в треугольнике.

На сторонах АС и ВС треугольника АВС отмечены точки К и М так, что АК:КС=m:n, BM:MC=p:q. Отрезки АМ и ВК пересекаются в точке О.

Через точку М проведем прямую, параллельную ВК. Она пересекает сторону АС в точке D, и согласно обобщению теоремы Фалеса

Пусть АК=mx. Тогда в соответствии с условием задачи КС=nx, а так как KD:DC=p:q, то 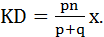Снова воспользуемся обобщением теоремы Фалеса:

Аналогично доказывается, что .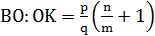

Теорема Чевы.

Теорема названа в честь итальянского математика Джованни Чевы, который доказал её в 1678 году.

Формулировка:

Если на сторонах АВ, ВС и СА треугольника АВС взяты соответственно точки С₁, А₁ и В₁, то отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке тогда и только тогда, когда

(3)

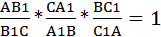
1. (3)

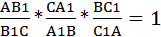
2.отрезки АА1, ВВ1 и СС1 пересекаются в одной точке

Доказательство:

1. Пусть отрезки АА1, ВВ1 и СС1 пересекаются в одной точке О. Докажем, что выполнено равенство (3). По теореме о пропорциональных отрезках в треугольнике имеем:

и .

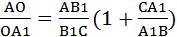
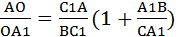
Левые части этих равенств одинаковы, значит, равны и правые части. Приравнивая их, получаем

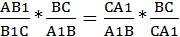
Разделив обе части на правую часть, приходим к равенству (3).

2. Докажем обратное утверждение. Пусть точки С1, А1 и В1 взяты на сторонах АВ, ВС и СА так, что выполнено равенство (3). Докажем, что отрезки АА1, ВВ1 и СС1 пересекаются в одной точке. Обозначим буквой О точку пересечения отрезков АА1 и ВВ1 и проведем прямую СО. Она пересекает сторону АВ в некоторой точке, которую обозначим С2. Так как отрезки АА1, ВВ1 и СС1 пересекаются в одной точке, то по доказанному в первом пункте

. (4)

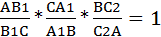
Итак, имеют место равенства (3) и (4).

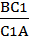
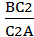
Сопоставляя их, приходим к равенству = , которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки C1 и C2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке O. Теорема доказана.

Теорема Менелая.

Формулировка:

Если на сторонах АВ и ВС и продолжении стороны АС (либо на продолжениях сторон АВ, ВС и АС) взяты соответственно точки С₁, А1, В1, то эти точки лежат на одной прямой тогда и только тогда, когда

(5)

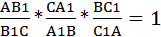
1. (5)

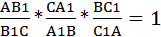
2. точки А1,С1,В1 лежат на одной прямой

Доказательство:

1. Пусть точки А1,В1 и С1 лежат на одной прямой. Докажем, что выполнено равенство (5). Проведем AD,BE и CF параллельно прямой В1А1 (точка D лежит на прямой ВС). Согласно обобщению теоремы Фалеса имеем:

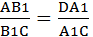
Перемножая левые и правые части этих равенств, получаем

, откуда ,

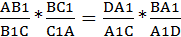
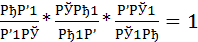
т.е. выполнено равенство (5).

2. Докажем обратное утверждение. Пусть точка В1 взята на продолжении стороны АС, а точки С1 и А1 – на сторонах АВ и ВС, причем так, что выполнено равенство (5). Докажем, что точки А1,В1 и С1 лежат на одной прямой, то по доказанному а первом пункте

(6)

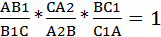
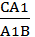
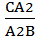
Сопоставляя (5) и (6), приходим к равенству = , которое показывает, что точки А1 и А2 делят сторону ВС в одном и том же отношении. Следовательно, точки А1 и А2 совпадают, и, значит, точки А1,В1 и С1 лежат на одной прямой. Аналогично доказывается обратное утверждение в случае, когда все три точки А1,В1 и С1 лежат на продолжениях соответствующих сторон. Теорема доказана.

Решение задач.

Задача №1.

Условие:

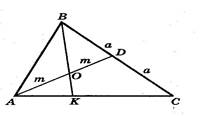
В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К.

Найти:

Решение: Пусть ВD = DС = а, АО = ОD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника АDС. По теореме Менелая получаем

Задача №2.

Условие:

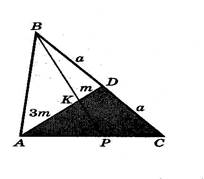
Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два.

Найти:

Решение: Пусть АD = DC = a, KD = m, тогда АК = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС. Необходимо найти

отношение 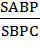. Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то

По теореме Менелая для треугольника ADC и секущей РВ имеем

Итак, .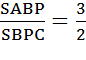

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Пропорциональные отрезки в прямоугольном треугольнике

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим пропорциональные отрезки в прямоугольном треугольнике. Соотношения между элементами прямоугольных треугольников позволяют легко вычислять неизвестные элементы прямоугольного треугольника. Мы сформулируем и докажем три теоремы, связывающие элементы прямоугольного треугольника, а также решим задачу на их применение.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»