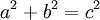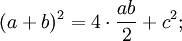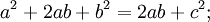Теорема пифагора подобие треугольников

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).

Через подобные треугольники

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
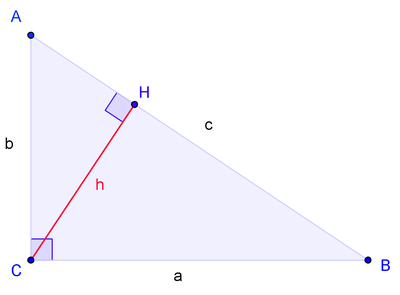
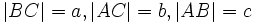
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

получаем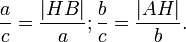

Что эквивалентно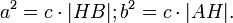

Сложив, получаем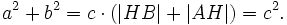

или

Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

1. Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.
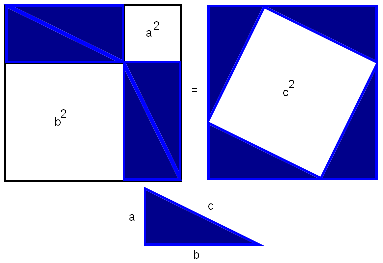
2. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
3. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и внутреннего квадрата.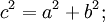



Что и требовалось доказать.

Доказательства через равносоставленность

Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах. Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK. Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°). Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично. Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах.

Доказательство Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части (так как треугольники ABC и JHI равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки, мы усматриваем равенство заштрихованных фигур CAJI и GDAB. Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна половине площади квадрата, построенного на гипотенузе, плюс площадь исходного треугольника. Последний шаг в доказательстве предоставляется читателю.

• Currently 2.97/5
• 1
• 2
• 3
• 4
• 5

Рейтинг: 3.0/5 (Всего оценок: 114)

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Теорема Пифагора

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Доказательство теоремы Пифагора. Способ 2. Через подобные треугольникиСкачать

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

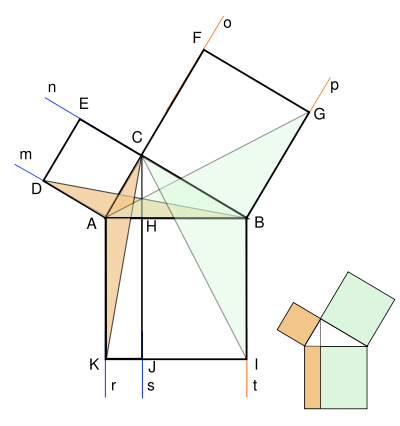
Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Видео:Самое простое Доказательство теоремы ПифагораСкачать

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Доказательство теоремы Пифагора, основанного на теории подобия

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Доказательство
теоремы Пифагора,
основанного на теории подобия
Выполнил: Дедов Кирилл, 8В
Руководитель: Макарова Т.П.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство через подобные треугольники.

Дано: АВС- прямоугольный треугольник

Доказать: АВ= АС+ВС
2
2
2
Доказательство
В прямоугольном треугольнике АВС проведем из вершины прямого угла высоту СН; тогда треугольник разобьется на два треугольника, также являющихся прямоугольными.

Треугольник ACH подобен треугольнику ABC по двум углам (по первому признаку подобия: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны):
Треугольники АВС и АСН, кроме прямого угла, имеют общий угол А.

Аналогично, треугольник CBH подобен ABC (общий угол В).
Малые треугольники также подобны друг другу, т.к. каждый из них подобен большому треугольнику.

Так как в подобных треугольниках соответственные стороны пропорциональны, то из подобия исходного треугольника и треугольника АСН следует
АН:АС=АС:АВ, или АС = АН∙АВ.

Теорема доказана.
Пользуясь терминами теории пропорций:
В прямоугольном треугольнике каждый катет есть средняя пропорциональная между гипотенузой и прилежащим к этому катету отрезком гипотенузы.

Аналогичное равенство, относящиеся к другому катету, имеет вид
ВС 2= НВ∙АВ.
Сложив оба равенства, получим
АС2+ВС2=АН ∙АВ+ВН ∙АВ = АВ(АН+ВН) = АВ2.

Мы пришли к доказательству теоремы Пифагора, основанному на теории подобия.
Оно встречается у индуса Басхара (род. В 1114 г. н. э.)
и затем у Леонарда Пизанского (в Practica geometriae, 1220 г.);
Позднее оно вновь было независимо найдено английским математиком Валлисом (1616-1703, Оксфорд).

Литература:
В. Литцман. Теорема Пифагора. М., 1960.

Задачи на применение
теоремы Пифагора

На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17м, чтобы верхний конец её достал до слухового окна, находящегося на высоте 15м от поверхности земли?
17м
15м

На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17м, чтобы верхний конец её достал до слухового окна, находящегося на высоте 15м от поверхности земли?
Дано: ▲АВС АВ=17м, АС=15м,
Найти: СВ
17м
?
С
В
А
15м

Задача древних индусов
Над озером тихим,
С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой,
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода
Здесь глубока?

На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Задача индийского
математика XII века
Бхаскари:

В новое время, особенно благодаря бурному развитию естествознания, астрономии и математики, идеи Пифагора о мировой гармонии приобретают новых поклонников. Великие Коперник и Кеплер, знаменитый художник и геометр Дюрер, гениальный Леонардо да Винчи, английский астроном Эддингтон, экспериментально подтвердивший в 1919 году теорию относительности, и многие другие ученые и философы продолжают находить в научно-философском наследии Пифагора необходимое основание для установления закономерностей нашего мира.

Курс повышения квалификации

Охрана труда

• Сейчас обучается 99 человек из 45 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 349 человек из 64 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 216 человек из 53 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 532 295 материалов в базе

Другие материалы

• 28.12.2020
• 2179
• 0

• 28.12.2020
• 2351
• 0

• 28.12.2020
• 2371
• 1

• 28.12.2020
• 2505
• 0

• 28.12.2020
• 2390
• 0

• 28.12.2020
• 2429
• 0

• 13.12.2020
• 1736
• 0

• 17.11.2020
• 1625
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 01.10.2020 231
• PPTX 150.5 кбайт
• 2 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Бауэр Марина Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 1 месяц
• Подписчики: 0
• Всего просмотров: 20220
• Всего материалов: 211

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Новые курсы: школьные службы примирения, детская журналистика и другие

Время чтения: 15 минут

Ученики 5-11 классов Воронежа перейдут на дистанционное обучение с 3 февраля

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

Все школы Оренбурга переводят на дистанционное обучение с 28 января

Время чтения: 1 минута

В Курганской области школьников переведут на дистанционное обучение с 4 февраля

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔥 Видео

Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Edu: Сколькими способами можно доказать теорему Пифагора?Скачать

Доказательство теоремы Пифагора (видео 23) | Подобие. Геометрия | МатематикаСкачать

Простое доказательство теоремы Пифагора. Понятнее, чем в учебникеСкачать

8 класс, 22 урок, Первый признак подобия треугольниковСкачать

8 класс, 16 урок, Теорема ПифагораСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Теорема ПифагораСкачать

Подобие треугольниковСкачать

Теорема ПифагораСкачать

ТЕОРЕМА ПИФАГОРА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать