Теорема о соотношении треугольников

Видео:7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

О многоугольнике с тремя сторонами

Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.

Таким образом, два ключевых элемента образуют рассматриваемую фигуру:

И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.

На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.

Существование фигуры

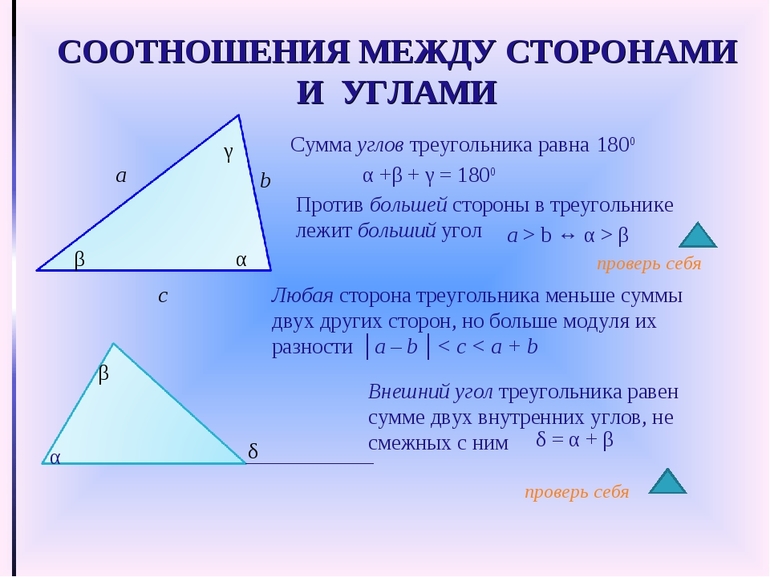
Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.

Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.

Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:

1. Остроугольные. В них все три угловые меры меньше 90 °. При этом возможны случаи взаимного их равенства, то есть каждый будет составлять 60 °. Такие треугольники называются равносторонними или правильными. Равны могут быть между собой также два угла, это будет уже равнобедренный треугольник, у которого боковые стороны имеют одинаковую длину.
2. Тупоугольные. Поскольку сумма составляет 180 °, то по определению в рассматриваемом многоугольнике не может быть больше одного тупого угла. Тупоугольные фигуры могут иметь либо произвольный тип, когда все их отрезки различаются, либо являться равнобедренными.
3. Прямоугольные. Это специальный тип треугольников, о котором известно многое, и который разграничивает два предыдущих типа. В них один угол равен 90 °, а два других являются острыми.

Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.

Важные линии

Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:

1. Медиана — делящий на две равные по площади части исходный треугольник. Отрезок проводится из вершины к середине противоположной стороны.
2. Биссектриса. Ею называют отрезок, который на две половины делит угол при произвольной вершине.
3. Высота. Этот элемент проводится также из вершины, но по отношению к противоположной стороне он является перпендикуляром. Таким образом, высота делит исходную фигуру на два прямоугольных геометрических объекта, которые в общем случае между собой не равны.
4. Медиатриса — это серединный перпендикуляр, то есть он сочетает свойства медианы и высоты, однако, через вершину треугольника он может не проходить. Медиатрисами пользуются при построении описанной окружности.
5. Средняя линия — это отрезок, который посередине пересекает две стороны треугольника. Его длина всегда будет в два раза меньше стороны фигуры, которой он параллелен. Средняя линия приводит к созданию подобной исходной фигуры, которая в два раза меньше.

Для правильных, равнобедренных и прямоугольных треугольников некоторые из названных отрезков могут совпадать друг с другом, а также со сторонами фигуры. Например, в прямоугольном треугольнике две малые стороны (катеты) также являются высотами.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Соотношение отрезков и углов

Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.

Большие и меньшие длины

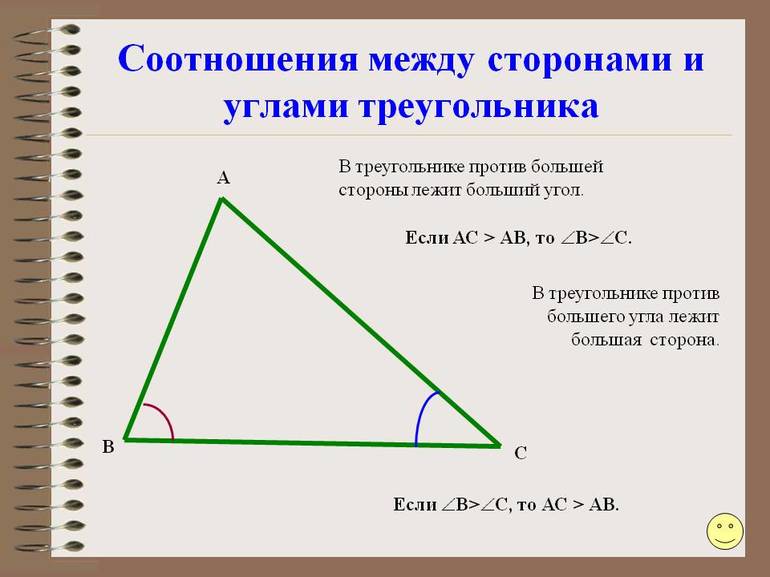
Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.

Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.

Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.

Рассмотренные теоремы приводят к двум важным следствиям:

1. Против равных сторон лежат равные углы, и наоборот. Следствие актуально для равносторонних и равнобедренных фигур.
2. Гипотенуза в треугольнике с прямым углом является самой длинной стороной, поскольку она лежит напротив самого большого угла.

Рассмотренные теоремы и их следствия активно используются при изучении подобных фигур. Поскольку напротив равных углов двух треугольников лежат соответствующие им длины отрезков, то последние будут попарно относиться друг к другу с определенным коэффициентом подобия.

Теоремы косинусов и синусов

Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:

c 2 = a 2 + b 2 — 2*a*b*cos©.

Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.

Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:

a/sin (A) = b/sin (B) = c/sin©.

Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).

Прямоугольный треугольник

Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:

Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 0,5 раза меньше гипотенузы:

sin (45 °) = a/c = ½ 0,5 .

Это соотношение можно получить также из теоремы Пифагора.

Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:

Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.

Таким образом, в любом треугольнике существует прямая пропорциональность между длиной стороны и противолежащим ей углом. Для количественного решения задач по геометрии с этой фигурой следует пользоваться выражениями синусов, косинусов и теоремой Пифагора.

Видео:Теорема о соотношении между сторонами и углами треугольника | Геометрия 7-9 класс #33 | ИнфоурокСкачать

Геометрия. 7 класс

Конспект урока

Соотношения между сторонами и углами треугольника. Неравенство треугольника

Перечень рассматриваемых вопросов:

• Установление соотношений между сторонами и углами треугольника.
• Формулирование неравенства треугольника.
• Теоремы о сравнении сторон и углов треугольника, их применение при решении задач.
• Проведение исследования о существовании треугольника с заданными элементами.

Каждая сторона треугольника меньше суммы двух других сторон.

В треугольнике против большей стороны лежит больший угол. Против большего угла лежит большая сторона.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее, на уроках геометрии, вы познакомились с различными фигурами, в том числе и с треугольником.

Сегодня мы продолжим изучать треугольники и рассмотрим соотношение между его элементами.

Теорема: В треугольнике против большей стороны лежит больший угол.

Отложим на стороне AB отрезок, равный стороне AC.

Угол 2 – внешний угол треугольника BDC, поэтому ∠2 > ∠B (по свойству внешнего угла треугольника).

∠1 = ∠2 как углы при основании равнобедренного ∆ADC (по свойству равнобедренного треугольника).

Справедлива и теорема, обратная данной. Против большего угла лежит большая сторона.

Предположим, что АВ = АС или АВ ∠ В.

Поэтому наше предположение неверное → AB > AC.

Докажем два следствия из этих теорем.

1 следствие. В прямоугольном треугольнике гипотенуза больше катета.

Дано: ∆АВС – прямоугольный.

Доказательство: ∠В > ∠А, т. к. ∠В = 90° ( по условию), ∠А –острый → АС > СВ (по обратной теореме о соотношениях между сторонами и углами треугольника: против большего угла лежит большая сторона).

Что и требовалось доказать.

Докажем второе следствие из этих теорем.

Если два угла треугольника равны, то треугольник равнобедренный. Это следствие называется признак равнобедренного треугольника.

Доказать: ∆АВС – равнобедренный

Докажем, что АВ = ВС.

Пусть АВ > ВС →∠С > ∠А (по теореме доказанной выше: против большей стороны лежит больший угол), противоречит условию, т. к. ∠А = ∠С . → АВ = ВС →∆АВС – равнобедренный (по определению равнобедренного треугольника).

Что и требовалось доказать.

Докажем теорему по соотношению между сторонами треугольника.

Каждая сторона треугольника меньше суммы двух других сторон.

Доказать: АВ ∠1 (так как угол 1 часть угла АВD), →∠ABD > ∠2 (так как ∠1 = ∠2).

Так как против большего угла лежит большая сторона (по теореме о соотношениях между сторонами и углами треугольника) → AB ВН (по обратной теореме о соотношениях между сторонами и углами треугольника).

Рассмотрим ещё случай АВ = ВС → ∆АВС – равнобедренный (по определению равнобедренного треугольника). То ВМ = ВН (по свойству равнобедренного треуголника, высота и медиана совпадают, если проведены к его основанию)→ ВМ ≥ ВН.

Что и требовалось доказать.

Разбор заданий тренировочного модуля.

1 Дано: ABC, равнобедренный, вычислите чему равна третья сторона треугольника, если две других равны 8 см и 4 см?

Объяснение: По определению равнобедренного треугольника, две его боковые стороны равны, следовательно это будет сторона равная 4 см или 8см.

Сторона 4см не может быть, т. к. 8см = 4 см + 4 см., что противоречит теореме о соотношениях между сторонами треугольника: каждая сторона треугольника меньше суммы двух других сторон.

Предположим, что боковые стороны равны 8 см. Тогда, по теореме о соотношениях между сторонами треугольника, каждая сторона треугольника меньше суммы двух других сторон, получим следующее соотношение между сторонами треугольника:

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Соотношения между сторонами и углами треугольника

Теорема 1 (о соотношениях между сторонами и углами треугольника).

• 1) Против большей стороны лежит большой угол.
• 2) Против большего угла лежит большая сторона.

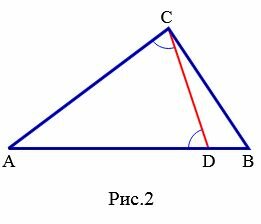
Доказательство. 1) Пусть задан треугольник ABC и пусть ( small AB > AC ) (Рис.1).

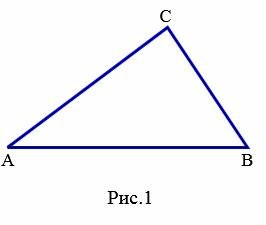Докажем, что ( small angle C gt angle B .)

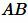
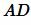
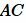
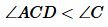Отложим на стороне отрезок , равной отрезку (Рис.2).

(1)

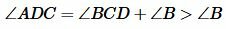(2)

Так как AC=AD, то треугольник ACD является равнобедренным и, следовательно

.

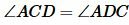(3)

Тогда из (1), (2) и (3) следует:

.

.

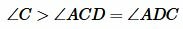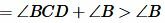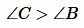Первая часть теоремы доказана.

2) Пусть в треугольнике ABC 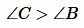. Докажем, что ( small AB > AC. )

Предположим обратное, т.е. 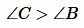но при этом ( small AB ≯ AC. ) Это значит либо ( small AB = AC, ) либо ( small AB AC. )

Следствие 1. В прямоугольном треугольнике гипотенуза больше катета.

Доказательство. В прямоугольном треугольнике напротив прямого угла (т.е. угла равного 90°) лежит гипотенуза. Остальные углы прямоугольного треугольника острые, проскольку сумма всех углов треугольника равна 180° (см. теорему статьи Сумма углов треугольника). Поскольку напротив острых углов стоят катеты и острые углы меньше 90°, то из части 2) теоремы 1 данной статьи следует, что гипотенуза больше катета.

Следствие 2 (Признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.

Доказательство. Пусть два угла треугольника равны. Тогда стороны лежащие напротив этих углов равны. Действительно. Если предположить, что стороны, лежащие напротив равных углов не равны, то по теореме 1, напротив большей стороны лежит большой угол, что противоречит условию следствия (что эти углы равны). Поскольку две стороны треугольника равны, то треугольник равнобедренный.

📺 Видео

Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

33. Соотношения между сторонами и углами треугольникаСкачать

Неравенства треугольника. 7 класс.Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

7 класс - Геометрия - Теорема о соотношениях между сторонами и углами треугольникаСкачать

Соотношения между сторонами и углами треугольника. Урок 10. Геометрия 9 классСкачать

Теорема о соотношении между сторонами треугольникаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

7 класс. Соотношения между сторонами и углами треугольника.Скачать

Соотношения между сторонами и углами треугольника. Практическая часть. 7 класс.Скачать

Соотношение между сторонами и углами треугольника. Решение треугольников. Урок 9. Геометрия 9 классСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Теорема Менелая | Математика | TutorOnlineСкачать

Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать