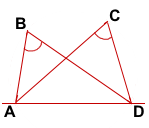
Теорема о четырех точках лежащих на окружности (4 видео)

Признак принадлежности четырёх точек одной окружности

Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

Доказать: точки A, B, C, D лежат на одной окружности

Обозначим ∠ABD=∠ACD=α.

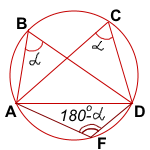
Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

Рассмотрим четырехугольник ACDF.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

Содержание

Углы и площади. Критерий принадлежности четырех точек одной окружности
Презентация на тему «Признак принадлежности четырёх точек одной окружности»
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Описание презентации по отдельным слайдам:
Дистанционное обучение как современный формат преподавания
Математика: теория и методика преподавания в образовательной организации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Материал подходит для УМК
Дистанционные курсы для педагогов
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
🎦 Видео

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Углы и площади. Критерий принадлежности четырех точек одной окружности

Условимся обозначать символом положительно ориентированный угол, на который надо повернуть вектор , чтобы он стал сонаправлен с вектором. Если и, то точкам Р и Q соответствуют комплексные числа b-а и d-c (рис.7) и:

Эта формула в применении к положительно ориентированному треугольнику АВС дает:

Если z=r( ,то Отсюда:

Выведем формулу для площади S положительно ориентированного треугольника АВС:

что можно записать в виде определителя третьего порядка:

Если треугольник АВС вписан в окружность , то формула (29) преобразуется к виду:

Для площади S положительно ориентированного четырехугольника ABCD имеем:

Если четырехугольник ABCD вписан в окружность zz=l, то (32) принимает вид:

Три произвольно взятые точки всегда принадлежат либо одной окружности, либо одной прямой. Критерии принадлежности трех точек одной прямой рассмотрены выше.

Докажем КРИТЕРИЙ принадлежности четырех точек одной окружности или прямой.

Возьмем четыре произвольные точки A, В, С, D соответственно с комплексными координатами а, b,c,d. Комплексное число:

называется двойным отношением точек A, В, С, D и обозначается (AB, CD). Порядок точек существен.

Теорема. Для того чтобы, четыре точки лежали на одной прямой или на одной окружности, необходимо и достаточно, чтобы их двойное отношение было действительным числом.

Доказательство. Если точки А, В, С, D коллинеарны, то отношения и действительные числа (см. условие (10)). Следовательно, в этом случае будет действительным и двойное отношение (34). Если точки А, В, С, D лежат на окружности, то рассмотрим два возможных случая:

точки С и D находятся в одной полуплоскости от прямой АВ;

точки С и D находятся в различных полуплоскостях от прямой АВ.

В первом случае ориентированные углы ВСА и BDA равны, во втором случае ВСА+АDВ= ±, т. е. ВСА-ВСА= ±. В обоих случаях разность равна нулю или ±. Но поскольку согласно (24) эта разность равна:

то — действительное число.

Обратно: если двойное отношение четырех точек действительно, то эти точки или коллинеарны, или принадлежат одной окружности. В самом деле, тогда если действительное число, то и действительное число. Поэтому точки А, В, С коллинеарны и точки А, В, D коллинеарны, и, значит, все четыре точки коллинеарны. Если же число комплексное, то и число также комплексное, отличное от действительного. Поэтому точки A, B, С неколлинеарны и точки А, В, D также неколлинеарны. Так как по условию двойное отношение вещественно, то:

Следовательно, либо BCA=BDA, либо ВСА— ВDА=±, т.е. ВСА+ADB=±. В первом случае отрезок АВ из точек С и D виден под равными углами, и, стало быть, они принадлежат одной дуге окружности, стягиваемой хордой АВ. Во втором случае сумма противоположных углов четырехугольника ACBD равна ±, и поэтому он будет вписанным в окружность. Доказательство закончено.

Задача 1. В окружности проведены три параллельные хорды Доказать, что для произвольной точки М окружности прямые образуют равные углы соответственно с прямыми ВС, СА, АВ.

Решение. Принимая окружность за единичную, отнесем точкам А, В, С, A₁, B₁, C₁ комплексные числа Тогда по условию (9) параллельности хорд имеем Следует доказать, что (рис.8).

Первое равенство эквивалентно такому:

т.е. эта дробь должна быть числом действительным. А это имеет место, поскольку сопряженное ей число:

равно этой же дроби. Аналогично доказывается и второе равенство углов.

Задача 2. На плоскости даны четыре окружности так, что окружности и пересекаются в точках и ; окружности и пересекаются в точках и , окружности и — в точках и и окружности и — в точках и . Доказать, что если точки лежат на одной окружности или прямой, то и точки также лежат на одной окружности или прямой (рис.9).

Решение. Согласно теореме этого параграфа и условию задачи будут действительными двойные отношения:

Поэтому будет действительным и число:

Следовательно, из вещественности двойного отношения вытекает вещественность и двойного отношения .

Видео:Доказать, что точки лежат на одной окружностиСкачать

Презентация на тему «Признак принадлежности четырёх точек одной окружности»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описанная и вписанная окружности четырёхугольника Автор: учитель математики Румянцева Р.Г.

Признак принадлежности четырёх точек окружности

Признак принадлежности четырёх точек окружности Если точки А, М, N, В таковы что угол АМВ равен углу АNВ, причём точки M и N лежат в одной полуплоскости относительно прямой АВ, то точки А, М, N, В лежат на одной окружности.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 937 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 305 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 496 839 материалов в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 10. Описанная и вписанная окружности четырёхугольника

Видео:Условие принадлежности четырёх точек одной окружностиСкачать

Дистанционные курсы для педагогов

Другие материалы

25.11.2020
54

24.11.2020
140

24.11.2020
160

24.11.2020
158

24.11.2020
143

24.11.2020
270

24.11.2020
156

24.11.2020
88

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

25.11.2020 1058 —> —> —> —>
PPTX 79.6 кбайт —> —>
Оцените материал:

Настоящий материал опубликован пользователем Румянцева Рита Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 5 лет и 2 месяца
Подписчики: 0
Всего просмотров: 2977
Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В школьном курсе мировой истории планируют уделить больше внимания Азии и Африке

Время чтения: 1 минута

Минпросвещения России запускает конкурс для учителей физкультуры

Время чтения: 2 минуты

Каждый второй российский студент недоволен своим вузом

Время чтения: 1 минута

Школы Сургута переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Свободное движение повышает креативность

Время чтения: 1 минута

В Сыктывкаре школьников переведут на дистанционное обучение

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.