Теорема микеля о трех окружностях (6 видео)

Теорема микеля о трех окружностях

И. Ф. Шарыгин. Нужна ли в школе 21-го века Геометрия? (pdf)
Матем. просв., сер. 3, 8, 2004 г.

А. Д. Блинков. Почему я не вызываю учеников к доске?(doc)
Статья написана в 2004 году к Международному конгрессу по образованию.

И. А. Кушнир. Эмоциональная геометрия (pdf)
Эмоциональная геометрия основана на коротких посильных и красивых задачах повышенной сложности. О таких задачах (в том числе, авторских) и пойдет речь.

И. Ф. Шарыгин. Избранные статьи djvu.

Статьи Игоря Фёдоровича в «Кванте» .

В. Протасов, В. Тихомиров. Геометрические шедевры Шарыгина (pdf) «Квант», №1, 2006 г.

Содержание

Cредняя линия. Параллелограмм
Квадраты
Вокруг биссектрисы
Теорема Штейнера-Лемуса
Вписанная и вневписанные окружности
Площадь
Прямая Эйлера и окружность девяти точек
Точка Микеля, прямая Симсона, прямая Штейнера, теорема Дроз-Фарни
Теорема Фейербаха и точка Фейербаха
Симедиана
Конструкции
Задача о бабочке
Построения
Гомотетия
Полувписанная окружность, окружности Тебо
Замечательные окружности
Трисекция. Теорема Морлея
Изогональное сопряжение
Теорема Кэзи
Комбинаторная геометрия
Геометрические неравенства
Замечательные кривые
Теорема Понселе
Алгебра и геометрия
Стереометрия
Теорема микеля о трех окружностях
Теорема Морли
Точки Микеля
Углы, окружности и подобные треугольники
Математика в Московском университете
Перестановки, пары таблиц Юнга и максимальные монотонные подпоследовательности
Ловушка для треугольника
Перестановки и пары таблиц Юнга
Новый взгляд на коники
Лингвистические задачи
Геометрия цепных дробей
Об одном математическом случае, или Штопор и бифуркации
«Экспериментальная математика»
Инверсия и построения одним циркулем
Задача Аполлония
Избранные задачи Всесоюзных олимпиад
Бесповторные последовательности
Площади прямоугольных треугольников. Метод бесконечного спуска
Об итерациях в геометрии, о предельных циклах и их бифуркациях
Теорема Холла о различных представителях, или Деревенские свадьбы
От средней линии треугольника до прямой Эйлера четырёхугольника
Лемма Турана
Теорема об арифметической прогрессии и числа Рамсея
Почему не уменьшается сопротивление?
Дерево Калкина-Вилфа
Гармонический ряд, или Собака бежит наперерез
Математика. Олимпиадные задания. Тренировка 78. Задания + решения. Прямая Симсона и точка Микеля Теорема.
📺 Видео

Cредняя линия. Параллелограмм

Г. Б. Филипповский. О двух параллелограммах в треугольнике. (pdf) «Квант», №4, 2008 г.

Квадраты

Е. Бакаев. Комбинации квадратов (pdf). «Квант», №7, 2018г.

А. Д. Блинков, Ю. А. Блинков. Угол в квадрате (pdf). «Квант», №4, 2015 г.

Е. Бакаев, А. Д. Блинков. Вспомогательные квадраты (pdf). «Квант», №4, 2016 г.

Вокруг биссектрисы

И. Ф. Шарыгин. Вокруг биссектрисы «Квант», №8, 1983 г.
«В этой статье собраны некоторые геометрические факты, прямо или косвенно связанные с биссектрисой треугольника.»

Теорема Штейнера-Лемуса

Л. Штейнграц. Новый взгляд на теорему Штейнера-Лемуса. (pdf) «Квант», №1, 2013 г.

Вписанная и вневписанные окружности

А.Д. Блинков, Ю.А. Блинков. Вневписанная окружность. (pdf) «Квант», №2, 2009 г. В статье излагаются классические факты о вневписанной окружности, обсуждаются задачи, в которых вневписанная окружность возникает самым неожиданным образом.

Г. Б. Филипповский. Замечательная прямая треугольника. (pdf) «Квант», №4, 2007 г. К статье рекомендуем подборку задач о вписанной окружности.

Ю. Билецкий, Г. Филипповский. О пользе вневписанных окружностей. (pdf)

А. Д. Блинков, Ю. А. Блинков. Две окружности в треугольнике, три окружности в треугольнике. (pdf) «Квант», №2, 2012 г.

А.А. Заславский, М. Панов О вписанной окружности прямоугольного треугольника (pdf) «Квант», №4, 2017 г.

П. А. Кожевников. Вневписанные окружности и дюжины точек.
21-я летняя конференция международного математического Турнира городов.

Фольклор Задача Ф. Ивлева. (pdf)
В заметке решение трудной и красивой задачи разбито на несколько подзадач, что позволяет использовать материал на кружке. Решения многих задач и различные обобщения можно найти в статье.

Huseyin Demir and Cem Tezer More on Incircles (pdf) Mathematics Magazine, Vol. 62, No. 2 (Apr., 1989), pp. 107-114

Площадь

Е. Бакаев. Площадь Треугольника (pdf)

«Квантик №2», 2012 год

А. Щетников. Параллелограмм и равенство площадей (pdf)

«Квантик №2», 2012 год

Прямая Эйлера и окружность девяти точек

И. Ф. Шарыгин, А. Ягубьянц. Окружность девяти точек и прямая Эйлера «Квант» №8, 1981 г. К этой статье рекомендуем такую серию задач.

И. А. Кушнир. Золотой ключ Леонарда Эйлера (pdf) «Математика в школах Украины», №13-15, 2012 г.
Рассказывается о приложениях окружности девяти точек для доказательства классических задач.

Д. В. Швецов. Важная лемма (pdf) «Квант» №5-6, 2012 г.

Л. А. Емельянов. Точка Шиффлера (pdf) «Математика в школе» №6, 2006 г.
Пусть $I$ – центр вписанной окружности треугольника $ABC$. Тогда прямые Эйлера треугольников $AIC$, $AIB$, $BIC$, $ABC$ пересекаются в одной точке!

Nguyen Minh Ha. A proof of Vittas’ Theorem and its converse (pdf)
Во вписанном четырёхугольнике $ABCD$ диагонали пересекаются в точке $P$. Тогда прямые Эйлера треугольника $APB$, $BPC$, $CPD$, $DPA$ пересекаются в одной точке.

Debdyuti Banerjee and Sayan Mukherjee. Neuberg Locus And Its Properties (pdf) Journal of Classical Geometry, Volume 2, 2013
Отметим все такие точки $P$, что прямые Эйлера треугольников $APB$, $BPC$, $CPA$ пересекаются в одной точке. Оказывается, что это ГМТ обладает многими интересными своствами.

Точка Микеля, прямая Симсона, прямая Штейнера, теорема Дроз-Фарни

Ю. А. Блинков. Точка Микеля(pdf)
Базовые факты о точке Микеля.

Michal Rol ́ınek and Le Anh Dung The Miquel Points, Pseudocircumcenter, and Euler-Poncelet Point of a Complete Quadrilateral (pdf), Forum Geometricorum Volume 14 (2014) 145–153.

Г. Б. Филипповский. Ґрунтовна розмова про пряму Симсона-Уоллеса
Увлекательный рассказ о всех основных свойствах прямой Симсона, разбирается большое количество примеров!

Д. В. Швецов. От прямой Симсона к теореме Дроз-Фарни (pdf)
Журнал «Квант», №6, 2010 г.

Е. Д. Куланин. О прямых Симсона, кривой Штейнера и кубике Мак-Кэя (pdf)
Ежегодник «Математическое просвещение», №10, М., 2006
Обстоятельная статья, в которой, например, изучается вопрос касания прямых Симсона окружности Эйлера.

Cosmin Pohoata and Son Hong Ta. A Short Proof of Lamoen’s Generalization of the Droz-Farny Line Theorem (pdf)
Теорему Дроз-Фарни можно обобщать в разных направлениях. Об одном таком и идёт речь в статье.

Titu Andreescu and Cosmin Pohoata Droz-Farny Demystified (pdf)
В статье приводится очень короткое доказательство красивого обобщения теоремы Дроз-Фарни.

Теорема Фейербаха и точка Фейербаха

В. Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) «Квант», №4, 2008 г.
В статье обсуждаются сразу две жемчужины: теорема Тебо и теорема Фейербаха. Оказывается, что одна из теорем является следствием другой!

П.А. Кожевников. Ещё раз о точке Фейербаха. (pdf) Математическое просвещение, Выпуск 15, 2012 г.
«В этой заметке предлагается геометрическое доказательство теоремы Фейербаха, которое дает возможность описать точку Фейербаха и, в частности, получить отличное от авторского геометрическое решение задачи 8 из задачного раздела «Математического просвещения», вып. 14, 2010 г.»

J.L. Ayme. Красивое доказательство теоремы Фейербаха. (pdf)
Очень красивое доказательство теоремы Фейербаха. Оригинал статьи можно посмотреть на странице автора.

Фольклор. Доказательство теоремы Фейербаха по И. Ф. Шарыгину. (pdf)

Nguyen Minh Ha and Nguyen Pham Dat. Synthetic Proofs of Two Theorems Related to the Feuerbach Point.(pdf) Forum Geometricorum Volume 12 (2012) 39–46. В статье излагаются геометрические доказательства двух замечательных теорем, связанных с точкой Фейербаха. Кроме цитированной статьи J. Vonk, рекомендуем заглянуть в статью Куланина Е. Д., в которой теорема Емельянова доказывается с помощью коник.

Jan Vonk. The Feuerbach point and reflections of the Euler line. (pdf) Forum Geometricorum, 9 (2009) 47—55.
Рассматриваются интересные свойства точки Фейербаха.

Куланин Е.Д., Шихова Н.А. Прямые Эйлера и точки Фейербаха.(pdf)
Математическое образование, №2, 2012.

Кожевников П. А.(по статье Д. Гринберга) Обобщение теоремы Фейербаха. (pdf)

Куланин Е. Д. Об описанных окружностях чевианных и педальных треугольников и некоторых кривых, связанных с треугольником. (pdf)
Ежегодник «Математическое просвещение», №9, М., 2005.
Доказательство теоремы Фейербаха через коники! В статье указывается целое семейство окружностей, проходящих через точку Фейербаха(например, окружность, проходящая через основания биссектрис, проходит через точку Фейербаха). Для понимания статьи необходим некоторый опыт работы с кониками, который можно получить, почитав замечательную книгу А. Акопяна, А. Заславского (pdf).

Симедиана

А. Карлюченко, Г. Филипповский. О касательных, проведённых в двух вершинах треугольника , (pdf)

Ю. Блинков. Симедиана (pdf), «Квант», №4, 2015 г.

Tran Quang Hung . A Simple Synthetic Proof of Lemoine’s Theorem (pdf)

Конструкции

В.Ю. Протасов. О двух велосипедистах и вишнёвой косточке (pdf) «Квант», №3, 2008 г. «Попробуем подвести некоторые итоги. Две задачи международных олимпиад, задача о бабочке, два десятка геометрических задач, которые мы сформулировали в виде упражнений (некоторые из них появлялись на математических олимпиадах, в Задачнике , и в различных сборниках задач). Список далеко не полный. И все это выросло из задачи 1, совсем простенькой и неинтересной, которую мы вначале и решать-то не хотели.»

Г. Б. Филипповский. О точке на стороне и двух параллельных (pdf) «Математика в школах Украины», №4, 2011 г.

А. Полянский. Воробьями по пушкам (pdf) «Квант», №2, 2012 г. Решения упражнений
«В этой статье мы пользуясь двумя простыми и элегантными фактами, решим две достаточно сложные задачи.»

Ю. А. Блинков Ортоцентр, середина стороны, точка пересечения касательных и ещё одна точка ! (pdf) «Квант», №2, 2014 г.

А. Карлюченко, Г. Филипповский. Задачи с тремя равными окружностями (pdf) «Математика в школах Украины», № 22-23, август 2014 г.

Г. Б. Филипповский. «Угловые» приключения барона Мюнхгаузена (pdf)

А. Карлюченко, Г.Б. Филипповский. Про вiдстанi вiд вершини трикутника до його чудових точок (pdf). «У світі математики», том 22, випуск 4, 2016 г.

Ф. Нилов. New Examples of Hexagonal Webs of Circles (pdf)

Задача о бабочке

А. В. Спивак. Десять бабочек (pdf)

Е. С. Горская. Шесть доказательств теоремы о бабочке (pdf) Сборник «Учим математике-2». МЦНМО, 2009 г.

Построения

Г. Б. Филипповский, А. Карлюченко На трёх параллельных прямых pdf

А. Д. Блинков Геометрические построения с помощью треугольника-шаблона (pdf) «Квантик», №3-4, 2012 г.

Е. Д. Куланин Еще раз о трисекции угла (pdf) «Математика в школах Украины», №4, 2012 г.

Гомотетия

А. Спиров. Неожиданная поворотная гомотетия (pdf) «Квант», №5, 1998 г.

П. А. Кожевников. Задача M2100 (pdf)

Рекомендуем такие интересные серии задач на гомотетию:

Ортоцентр, середина стороны, точка пересечения касательных и … еще одна точка! (pdf)

Полувписанная окружность, окружности Тебо

В. Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) «Квант», №4, 2008 г.

Рекомендуем серию задач про полувписанную окружность:
полувписанная окружность

А. Львов. О центрах гомотетий вписанных окружностей и окружностей Тебо pdf

Wilfred Reyes. An Application of Thebault’s Theorem (pdf) Forum Geometricorum Volume 2 (2002) 183–185.

Dmitry S. Babichev. Circles touching sides and the circumcircle for inscribed quadrilaterals (pdf) Journal of Classical Geometry, Volume 1, 2012

Замечательные окружности

Очень советуем порешать замечательную подборку задач Д. В. Прокопенко.

А. Г. Мякишев. Прогулки по окружностям: от Эйлера до Тейлора(pdf)

Jan Vonk and J. Chris Fisher. On a new circle associated with a triangle (pdf) Forum Geometricorum Volume 11 (2011) 13–26.
В статье, посвящённой окружности Фурмана, очень много красивых геометрических доказательств.

Трисекция. Теорема Морлея

Л. Емельянов, Т. Емельянова Теорема Морлея. Сто лет спустя «Математика в школе», 2004 год.

Тоноян Г., Яглом И. Теорема Морлея «Квант» №8, 1978 год.

Е. Д. Куланин Еще раз о трисекции угла (pdf) «Математика в школах Украины», №4, 2012 г.

Изогональное сопряжение

Для первого знакомства с темой рекомендуем книжку В. В. Прасолова и статью Д. Гринберга(ниже).

Д. Гринберг. Isogonal conjugation with respect to a triangle (zip)

А. В. Акопян, А. А. Заславский. Разные взгляды на изогональное сопряжение (pdf) Математическое просвещение, сер. 3, вып. 11, 2007.

Д. В. Прокопенко Изогональное сопряжение и педальные треугольники pdf «Квант» №9, 2017 год.

А. Куликова, Д.В. Прокопенко Теорема об изогоналях pdf , «Квант», №4-5, 2018 год
» В статье приведено доказательство теоремы и продемонстрирована эффективность применения этой теоремы в олимпиадных задачах высокого уровня»

Dimitar Belev. Some Properties of the Brocard Points of a Cyclic Quadrilateral (pdf), Journal of Classical Geometry, volume 2, 2013

A. В. Акопян. Conjugation of lines with respect to a triangle (pdf), Journal of Classical Geometry, volume 1, 2012
В статье речь идёт об обобщениях изогонального и изотомического сопряжениях. Для понимания статьи нужны знани проективных преобразований и коник. Всё необходимое можно найти в книжке про коники.

Теорема Кэзи

Luis Gonzlez. Casey’s Theorem and its Applications (pdf)

Shay Gueron. Two Applications of the Generalized Ptolemy Theorem (pdf)

Shailesh Shirali. On the Generalized Ptolemy Theorem (pdf)

Л. Емельянов. Замечательная окружность (pdf)

Комбинаторная геометрия

В. Ю. Протасов Теорема Хелли и вокруг неё (pdf) «Квант», №3, 2009 г.

Н. Б. Васильев Формула Пика «Квант», №12, 1974 г. Для дальнейшего знакомства с этим сюжетом рекомендуем книжку Вавилова и Устинова «Многоугольники на решетках»(pdf).

А. Полянский Одной рукой узелок не развяжешь ! (pdf) «Квант» №3, 2013 год.

А. Спивак, М. Смуров Покрытие полосками (часть-1) и (часть-2) «Квант», №4-5, 1998 г.

М. Петкова Салфетки «Кванта» и теорема Пифагора (pdf) «Квант» №3, 2012 год.

С. Табачников, В. Тиморин Прямая Сильвестра(pdf) «Квант», №5, 2009 г.

Геометрические неравенства

В. Протасов, В. Тихомиров Пространство Lp и замечательные точки треугольника (pdf) «Квант», №2, 2012 г.

Claudi Alsina, Roger B. Nelsen. Геометрическое доказательство неравенства Эрдеша-Морделла.(pdf)
Forum Geometricorum, 7 (2007) 99-102. В статье излагается одно из самых красивых доказательств известного неравенства.

Замечательные кривые

Акопян А. В. Кардиоида. «Квант» №3, 2012 год.

Теорема Понселе

Протасов В. Ю. Два века теоремы Понселе (pdf), Журнал «Квант» №5-6, 2014 г.

Протасов В. Ю. Обобщенные теоремы о замыкании (pdf) / Generalized closing theorems (pdf)

Е.Диомидов, А.Заславский, В.Калашников, Г.Челноков. Вокруг теоремы Понселе. Материалы ЛКТГ, 2014 г.

Белухов Н. И. The Mixed Poncelet-Steiner Closure Theorem. (pdf)

Алгебра и геометрия

Г. Б. Филипповский. Рене Декарт (1596–1650). Декартова система координат (pdf) «Математика в школах Украины», №35-36, 2011 г.

А.И. Сгибнев. «Геометрия помогает алгебре» (ps, 2M), (ps-zip, 400K), (pdf, 190K)

Стереометрия

В.Ю. Протасов. Выход в пространство-2 pdf «Квант» №1-2, 2018 г.

С. Кузнецов. Расстояния на сфере pdf «Квант» №4, 2017 г.

А. Заславский. Описанная и вписанные сферы тетраэдра «Квант» №1, 2004 год.

А. Заславский, Д. Косов. Изогонально сопряжение в тетраэдре и его гранях «Квант» №3, 2004 год.

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Теорема микеля о трех окружностях

Лекция 1 (245) 18.09.2010

Виктор Васильевич ПРАСОЛОВ,

автор книг «Геометрия Лобачевского», «Задачи по планиметрии», «Задачи по алгебре, арифметике и анализу», «Многочлены», «Наглядная топология», «Точки Брокара и изогональное сопряжение», «Элементы комбинаторной и дифференциальной топологии», «Элементы теории гомологий», соавтор книги «Узлы, зацепления, косы и трёхмерные многообразия» и соавтор книги «Геометрия».

Теорема Морли

Теорема Франка Морли утверждает, что при пересечении трисектрис углов любого треугольника образуется правильный треугольник. Были рассказаны сравнительно простые доказательства этой теоремы, появившиеся давно.

Доказательство можно найти в книге Г.С.М. Коксетера и С.Л. Грейтцера «Новые встречи с геометрией».

Лекция 2 (246) 25.09.2010

Алексей Александрович ЗАСЛАВСКИЙ,

старший научный сотрудник ЦЭМИ РАН, председатель жюри Всероссийской олимпиады по геометрии имени И.Ф. Шарыгина.

Точки Микеля

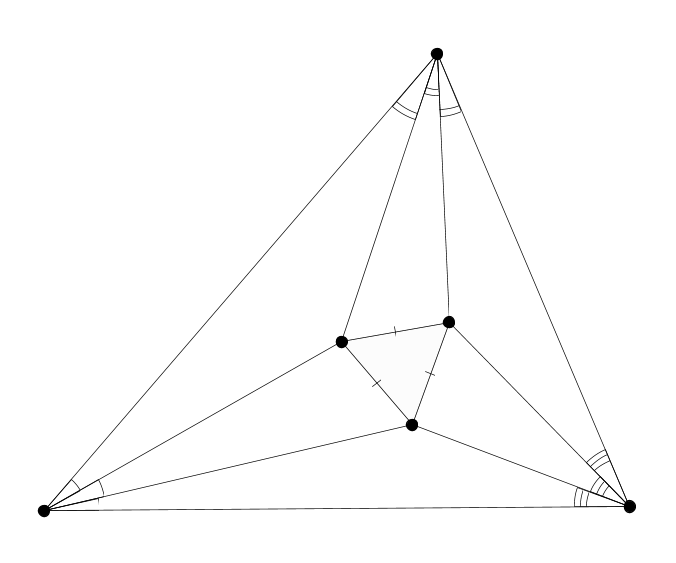
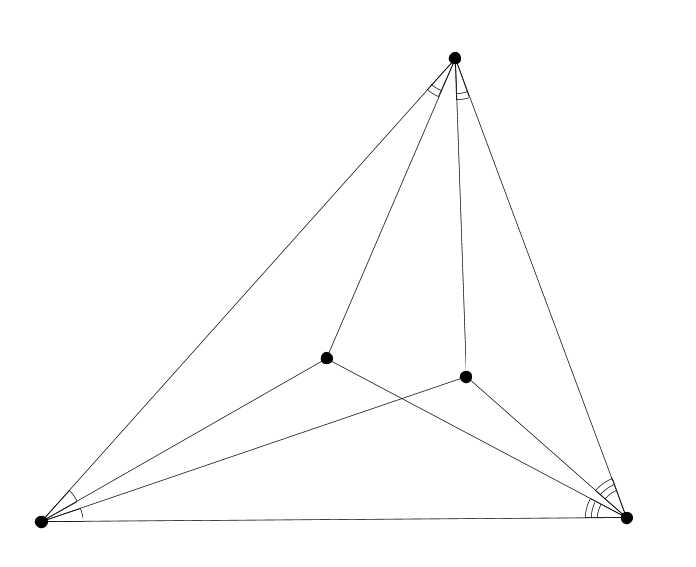
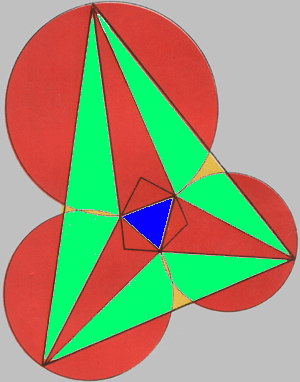
Пусть даны четыре прямые общего положения. Тогда четыре окружности, описанные около образованных ими треугольников, пересекаются в одной точке, которая называется точкой Микеля.

Рассмотрим теперь четыре точки. Соединяя их в разном порядке, можно получить три различных четырёхугольника (возможно, самопересекающихся). Стороны каждого из этих четырёхугольников определяют свою точку Микеля. Полученная конфигурация обладает рядом красивых свойств. Они были обнаружены П. Кожевниковым, Н. Белуховым и автором. Изучались на Летней конференции Турнира городов в августе 2010 года.

Лекция 3 (247) 2.10.2010

Юрий Викторович САДОВНИЧИЙ,

профессор кафедры общей топологии и геометрии мехмата МГУ, доктор физико-математических наук, автор книг и пособий для школьников.

Углы, окружности и подобные треугольники

Был изложен теоретический материал и рассмотрены интересные (в том числе и сложные) задачи, касающиеся равенств углов, а также отношений длин отрезков, которые из этих равенств вытекают. Можете ознакомиться с условиями и решениями этих задач.

Лекция 4 (248) 9.10.2010

Игорь Николаевич МОЛОДЦОВ,

заместитель декана мехмата МГУ, профессор.

Математика в Московском университете

В рамках «Фестиваля науки» И.Н. Молодцов выступил перед школьниками и их родителями.

Лекция 5 (249) 16.10.2010

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», преподаватель Малого мехмата, учитель школ

Перестановки, пары таблиц Юнга и максимальные монотонные подпоследовательности

Было рассказано о связи между перестановками и таблицами Юнга и доказано, что для любых натуральных чисел m и n в любой перестановке чисел есть убывающая подпоследовательность длины или возрастающая подпоследовательность длины

Лекция 6 (250) 23.10.2010

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и преподаватель Малого мехмата, учитель школ

Ловушка для треугольника

В третьем номере «Кванта» 1999 года опубликована статья В.Н. Дубровского и В.А. Сендерова «Ловушка для тругольника». В ней рассказано о том, как находить расстояния между замечательными точками треугольника и почему корнями уравнения

x 3 – px 2 + ( r 2 + 4 rR ) x = r 2 p ,

где p — полупериметр, а r и R — соответственно, радиусы вписанной и описанной окружностей, являются числа и где a , b и длины сторон треугольника. Именно при помощи этого уравнения легко доказать существование треугольника, ортоцентр (точка пересечения высот) и центр тяжести (точка пересечения медиан) которого лежат на его вписанной окружности.

Лекция 7 (251) 30.10.2010

Александр Васильевич СПИВАК,

Перестановки и пары таблиц Юнга

Окончание лекции, прочитанной 16 октября 2010 года. Было рассказано о свойствах таблиц Юнга. Полезно прочитать статью «Формула крюков» третьего номера «Кванта» 2009 года.

Лекция 8 (252) 6.11.2010

Фёдор Константинович НИЛОВ,

студент III курса мехмата МГУ.

Новый взгляд на коники

Хорошо известны два определения эллипса с помощью двух фокусов (множество точек, сумма расстояний до которых равна данной величине) и фокуса с директрисой (множество точек, расстояние от которых до фокуса равно произведению эксцентриситета, который меньше единицы, на расстояние до данной прямой, называемой директрисой). Основная мысль лекции состояла в том, что в этих определениях фокусы можно заменять на окружности, а расстояние от точки до на длину касательной:

Аналогичные определения можно дать для гипербол и парабол.

Были рассказаны два применения этих определений. Рассмотрим две окружности ω₁ причём ω₂ лежит строго Рассмотрим множество E эллипсов, каждый из которых вписан в ω₁ (касается в двух точках) и описан около ω₂. Тогда все эллипсы из E подобны; их фокусы лежат на одной окружности, концентричной для любых двух эллипсов из E диагонали криволинейного четырёхугольника, образованного их пересечением, перпендикулярны:

Другим применением является обобщение конструкции шаров Данделена на случай эллипсоида вращения.

Лекция 9 (253) 13.11.2010

Светлана Анатольевна БУРЛАК,

кандидат филологических наук, старший научный сотрудник Института востоковедения РАН и филологического факультета МГУ, член оргкомитета Московской олимпиады по лингвистике и математике, автор многих олимпиадных задач по лингвистике.

Лингвистические задачи

Стало традицией незадолго до Традиционной лингвистической олимпиады знакомить слушателей лектория Малого с тем, что такое лингвистика, демонстрировать примеры лингвистических задач. Задачи лингвистической олимпиады это значит, что для их решения специальные знания, достаточно лишь уметь логически рассуждать. В этом лингвистика похожа на математику: при описании языка требуется доказывать каждое предположение. Как и в прошлые годы, говорили о том, что такое язык и как его описывают. Но задачи, разумеется, были новые!

Если вам нравится разбираться в устройстве добро пожаловать на Традиционную лингвистическую олимпиаду.

Лекция 10 (254) 20.11.2010

Олег Николаевич ГЕРМАН,

доцент кафедры теории чисел, преподаватель СУНЦ МГУ.

Геометрия цепных дробей

Цепные дроби — математическая конструкция, в скрытом виде встречающаяся в самых неожиданных местах: от до переговорного устройства в лифтах МГУ. Обычно цепные дроби определяют при помощи алгебры, мы же рассмотрели этот объект с геометрической точки зрения. Методы геометрии чисел позволяют доказать многие фундаментальные свойства цепных дробей и классические теоремы.

Лекция 11 (255) 27.11.2010

Сергей Владимирович ДВОРЯНИНОВ,

кандидат физико-математических наук, доцент, автор статей журналов «Квант», «Потенциал», «Математическое образование», «Математика в школе», «Математика для школьников» и газеты «Математика».

Об одном математическом случае, или Штопор и бифуркации

На уроках математики решают задачи с параметрами. В физике изучают положения равновесия. детские качели. «Нелинейные» качели интереснее обычных: при разных значениях параметра уравнение может иметь разное количество корней. При изменении параметров механической системы положения равновесия могут исчезать и появляться. Подобные явления называют бифуркациями. Бифуркации были проиллюстрированы при помощи штопора. Было рассказано о статье «Об одном математическом случае», опубликованной в четвёртом и пятом номерах «Кванта» 2005 года.

Лекция 12 (256) 4.12.2010

Александр Владимирович ЖУКОВ,

ведущий рубрики «»Квант» для младших школьников» журнала «Квант» в 1998–2007 годах, автор книги «Вездесущее число π»

«Экспериментальная математика»

Компьютерная графика — сравнительно молодое направление экспериментальной математики. Компьютер может стать чудодейственным инструментом, позволяющим увидеть многие закономерности. На примере простейших алгоритмов («стежок», о котором рассказано в пятом номере «Кванта» 1992 года, а также различные отображения натурального ряда и динамические модели) были проиллюстрированы как широко известные, так и ещё до конца свойства чисел.

Лекция 13 (257) 11.12.2010

Александр Васильевич СПИВАК,

Инверсия и построения одним циркулем

Было рассказано о том, что такое инверсия, показана её связь со стереографической проекцией. Были доказаны важнейшие свойства инверсии и неожиданная теорема: линейка для геометрических построений! (Конечно, прямую без линейки но если задавать прямую при помощи пары точек на ней, то линейка действительно

Лекция 14 (258) 18.12.2010

Александр Васильевич СПИВАК,

Задача Аполлония

Как по трём данным окружностям (в роли каждой из которых может выступить и точка, и прямая) построить окружность или прямую, касающуюся всех трёх? Эта и многочисленные другие задачи на построение могут быть решены при помощи инверсии.

Лекция 15 (259) 12.02.2011

Александр Васильевич СПИВАК,

Избранные задачи Всесоюзных олимпиад

Было рассказано о недавно переизданной книге «Задачи Всесоюзных олимпиад» и разобрано несколько очень красивых задач.

Лекция 16 (260) 19.02.2011

Александр Васильевич СПИВАК,

Бесповторные последовательности

Слово Туэ задано очень простым рекуррентным правилом, однако оно приводит к явному примеру бесквадратной последовательности букв трёхбуквенного алфавита. Можно доказать существование бесконечного бесповторного слова и другим способом, о котором тоже было рассказано.

Лекция 17 (261) 26.02.2011

Александр Васильевич СПИВАК,

Площади прямоугольных треугольников. Метод бесконечного спуска

Не существует ни одного прямоугольного треугольника, длины всех сторон рациональные числа, а площадь площадь равняться и многим другим числам. Лекция посвящена методу бесконечного спуска, который позволяет доказывать факты такого рода.

Лекция 18 (262) 5.03.2011

Сергей Владимирович ДВОРЯНИНОВ,

кандидат физико-математических наук, доцент, автор статей журналов «Квант», «Потенциал», «Математика для школьников», «Математика в школе», «Математическое образование» и газеты «Математика».

Об итерациях в геометрии, о предельных циклах и их бифуркациях

ИТЕРАЦИЯ (от латинского iteratio — повторение) — многократное применение какой-либо математической операции. Итерации возникают, например, в задаче построения общего перпендикуляра к двум скрещивающимся прямым линиям в пространстве. Предельный цикл возникает при переходе с одной стороны правильного треугольника на другую по перпендикуляру.

Лекция 19 (263) 19.03.2011

Александр Васильевич СПИВАК,

Теорема Холла о различных представителях, или Деревенские свадьбы

Одна из важнейших теорем комбинаторики — теорема Холла о различных представителях, она же — теорема о сватовстве. Она помогает решать довольно разнообразные задачи и многократно переоткрывалась в разных конкретных ситуациях.

Лекция 20 (264) 26.03.2011

Дмитрий Викторович ШВЕЦОВ,

учитель школы №179.

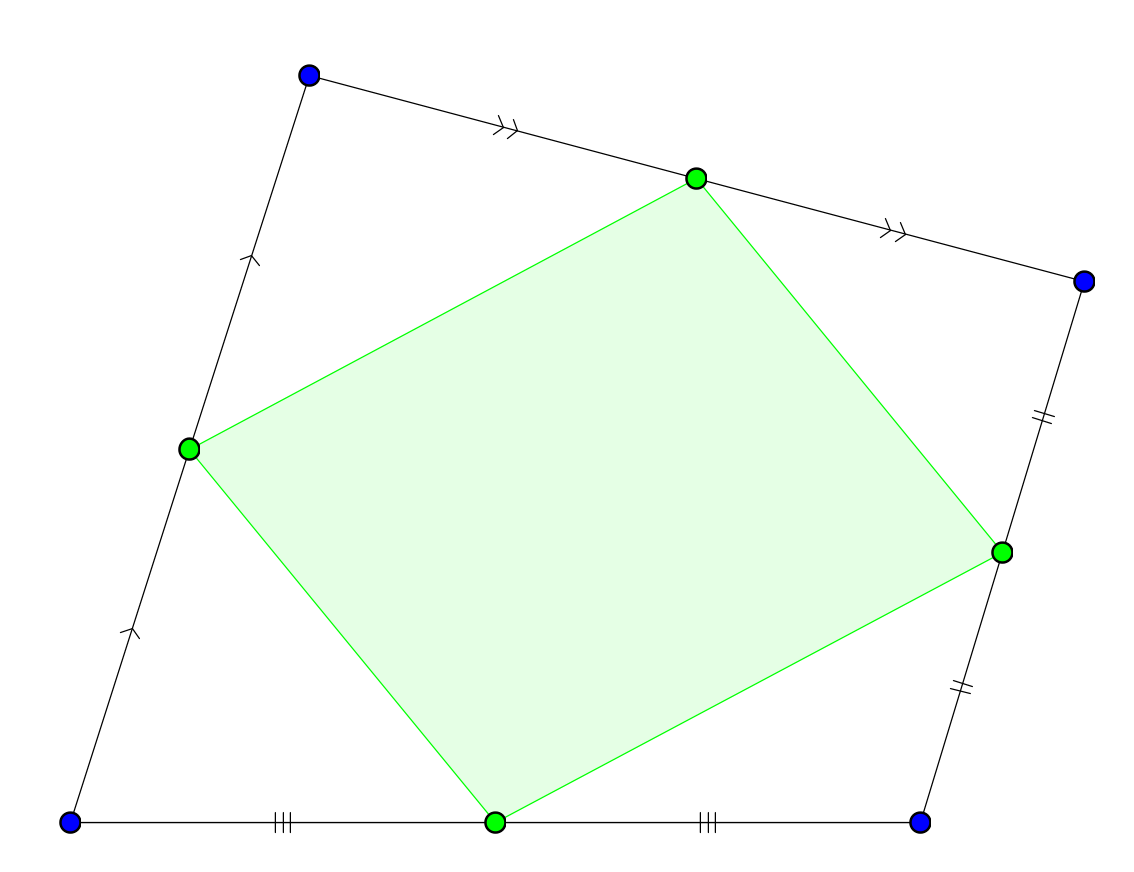
От средней линии треугольника до прямой Эйлера четырёхугольника

Прямая Эйлера и окружность девяти точек треугольника довольно известны любителям элементарной геометрии. Аналогичные объекты для четырёхугольника гораздо менее популярны. Мы восполним этот пробел. Для понимания достаточно знать теорему о средней линии треугольника и свойства вписанных углов.

Лекция 21 (265) 2.04.2011

Владимир Викторович ТРУШКОВ,

преподаватель Костромской летней многопредметной школы, Курганской летней математической школы, преподаватель Университета города Переславля.

Лемма Турана

Специалистов по теории графов часто интересует вопрос: как наибольшее количество рёбер может быть в графе на удовлетворяющем некоторому свойству? Например, каким может быть число рёбер в графе, заданного Впервые такую задачу поставил в 1941 году венгерский математик Пал Туран (1910–1976), который решил её, когда полный подграф на Было рассказано решение этой задачи и обсуждён случай, когда полный двудольный граф (каждый из соединён с каждым из Применение этой теории было проиллюстрировано на многих задачах разных олимпиад:

22 школьника участвовали в съезде юных писателей. После съезда каждый из них прочитал произведения трёх юных писателей, побывавших на съезде. Докажите, что из делегатов съезда можно составить комиссию из так, что в комиссии никто произведения остальных её членов.
В группе из n 2 человек каждый имеет n знакомых среди остальных. Докажите, что можно выбрать никакие двое из которых друг с другом.
В коллективе из 30 человек любых троих можно усадить за круглый стол таким образом, что каждый будет сидеть со своим знакомым. Докажите, что в этом коллективе найдётся компания из 10 человек, в которой каждый знаком с каждым.
В графе на 300 вершинах степень каждой вершины Докажите, что можно выбрать никакого два из которых общей вершины.
В кружке 20 учеников. Среди них есть ученик, имеющий среди кружковцев одного друга; ученик, имеющий среди кружковцев двоих друзей; . ; ученик, имеющий среди кружковцев Докажите, что найдутся трое кружковцев, каждые два из которых дружат.
В графе 34 вершины, степень каждой и для каждой вершины есть ровно одна вершина той же степени. Докажите, что в этом графе есть три вершины, попарно соединённые ребрами.
На конгресс приехало 100 ученых, каждый из которых сделал доклад. В конце каждый заявил, что ему понравилось сделанных его коллегами. Докажите, что найдутся четверо, каждому из которых понравились доклады двух других.
В стране 210 городов и совсем нет дорог. Король хочет построить несколько дорог с односторонним движением так, чтобы для любых трёх городов A , B , C , между которыми есть дороги, ведущие из A в B и из B в C , бы дороги, ведущей из A Какое наибольшее число дорог он сможет построить?
Рёбра графа на 300 вершинах покрашены в красный и синий цвета так, что нет одноцветного треугольника. Какое наибольшее число рёбер может быть в таком графе?

Лекция 22 (266) 9.04.2011

Александр Васильевич СПИВАК,

Теорема об арифметической прогрессии и числа Рамсея

Если натуральный ряд раскрасить в два цвета, то найдётся сколь угодно длинная арифметическая одноцветная прогрессия. Если рёбра полного графа на 17 вершинах раскрашены в то найдётся одноцветный треугольник.

Лекция 23 (267) 16.04.2011

Александр Васильевич СПИВАК,

Почему не уменьшается сопротивление?

При увеличении сопротивления любого провода электрической цепи постоянного тока (например, при перерезании этого провода) сопротивление цепи не может уменьшиться. Эта очевидная для любого физика теорема нуждается в математическом доказательстве. Доказательство основано на рассмотрении квадратичной функции многих переменных: энергии, выделяемой при протекании тока по цепи. Прочитать его можно в первом номере журнала «Квант» 1985 года.

Лекция 24 (268) 23.04.2011

Александр Васильевич СПИВАК,

Дерево Калкина-Вилфа

Множество точек плоскости с натуральными координатами счётно. Счётно и положительных рациональных чисел. В обоих случаях взаимно-однозначное соответствие задаётся очень естественным и красивым способом. Советую статью «По порядку становись!» второго номера журнала «Квант» 2008 года.

Лекция 25 (269) 30.04.2011

Александр Васильевич СПИВАК,

Гармонический ряд, или Собака бежит наперерез

Сумма величин, обратных первым n натуральным числам, стремится к бесконечности при А сумма ряда обратных квадратов конечна. М.Л. Гервера «Собака бежит наперерез» третьего номера «Кванта» 1973 года из этих фактов выведено решение задачи Радо о дрессировщике, убегающем на арене цирка от льва, скорость которого в точности равна скорости дрессировщика.

Было рассказано и содержание статьи М.Л. Гервера «Про лису и собаку» второго номера «Кванта» 1973 года.

Видео:Вебинар 3. Лемма о трезубце. Теорема Менелая, Чевы, Ван - Обеля. Свойства ортоцентра.Скачать

Математика. Олимпиадные задания. Тренировка 78. Задания + решения. Прямая Симсона и точка Микеля Теорема.

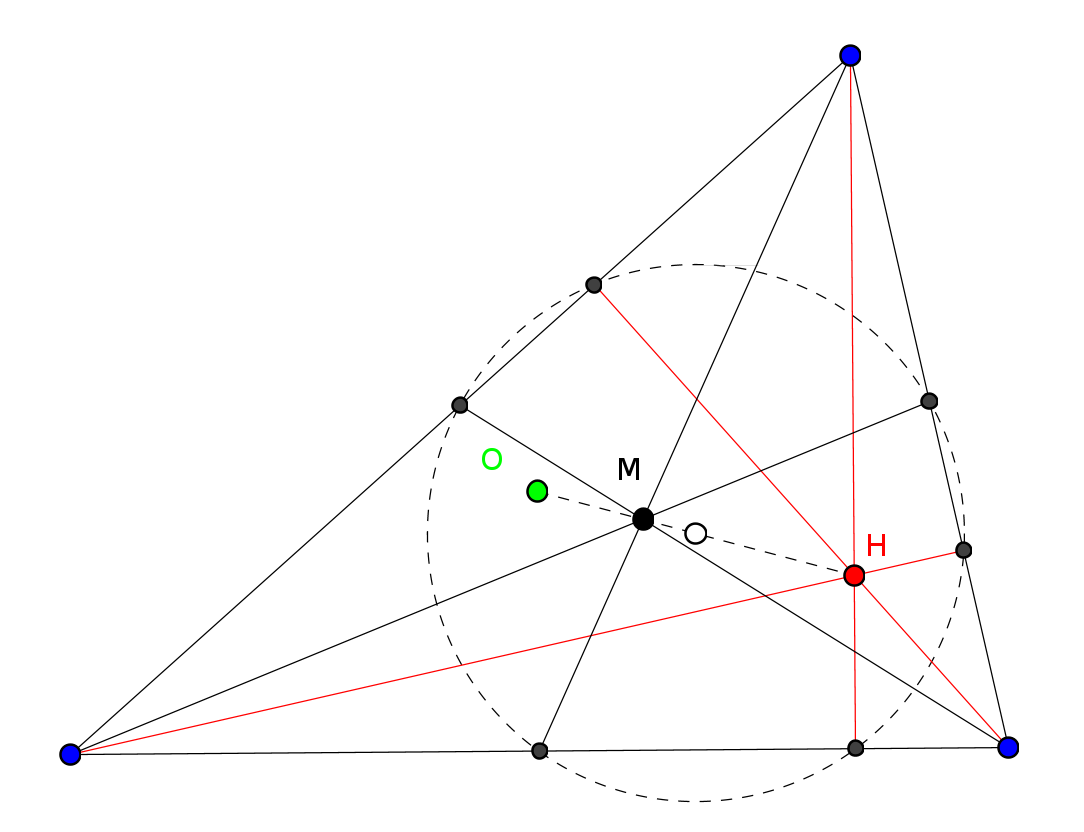
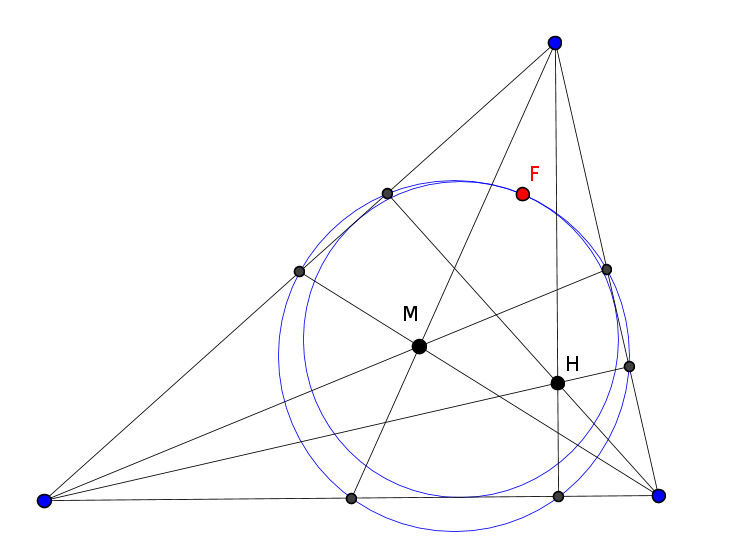
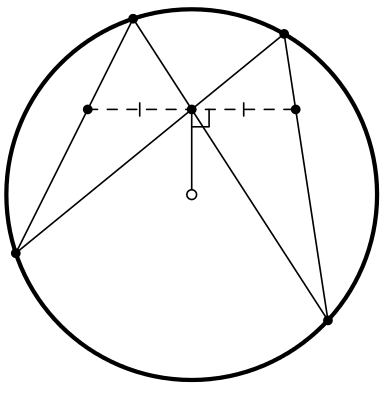
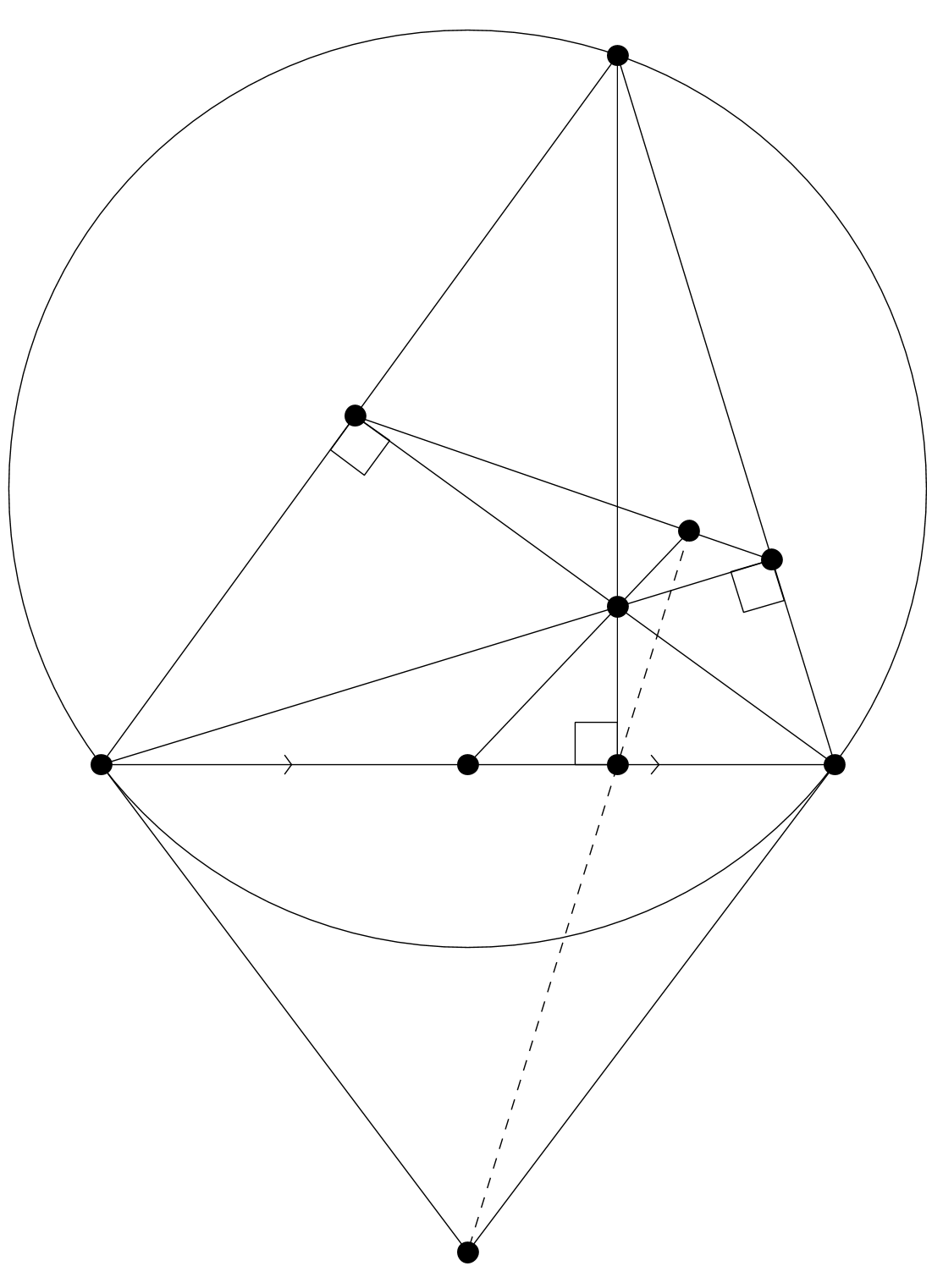
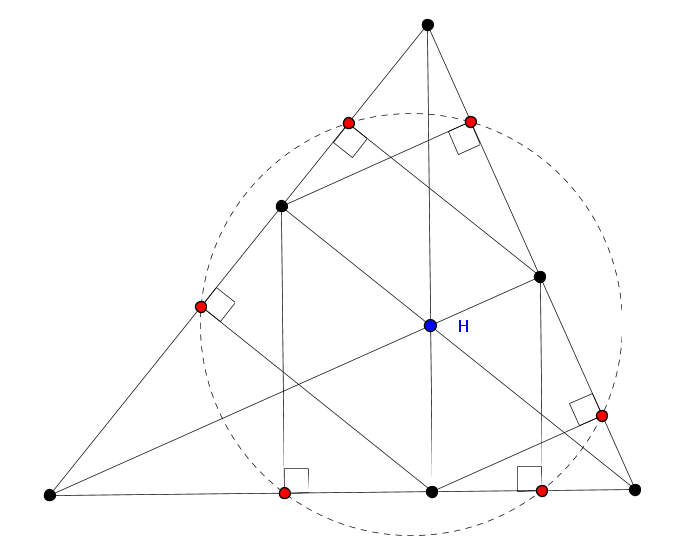
Основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), коллинеарны, т.е. лежат на одной прямой (прямая Симсона).

Роберт Симсон (1687-1768) – шотландский математик. А теорему доказал в 1797г. Вильям Уоллес.

Теорема Микеля о четырех прямых.

Четыре прямые общего положения при пересечении образуют четыре треугольника. Описанные около этих треугольников окружности пересекаются в одной точке. Эта точка называется точкой Микеля полного четырехсторонника.

Пусть четыре прямые расположены так (в общем положении), что при их пересечении образуется четыре треугольника. Тогда описанные вокруг этих треугольников окружности имеют общую точку, которая называется точкой Микеля этой конфигурации прямых.