Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- Описание презентации по отдельным слайдам:
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Дистанционные курсы для педагогов
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Как построить вписанную окружность треугольника
- Окружность, вписанная в треугольник. Теоремы и их рассмотрение
- Окружность, вписанная в равнобедренный треугольник
- Окружность, вписанная в прямоугольный треугольник
- Формулировка теоремы о вписанной окружности
- Теорема о центре окружности, вписанной в треугольник
- Окружность, вписанная в треугольник
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционные курсы для педагогов
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Построение с помощью циркуля и линейки — описание, алгоритмы и задачи
- Построение отрезка, равного данному
- Деление отрезка пополам
- Построение угла, равного данному
- Построение перпендикулярных прямых
- Пример 1
- Пример 2
- Построение параллельных (непересекающихся) прямых
- Построение правильного треугольника, вписанного в окружность
- Построение правильного четырехугольника вписанного в окружность
- Вариант 1
- Вариант 2
- Построение вписанного в окружность правильного пятиугольника
- Построение правильного шестиугольника, вписанного в окружность
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Окружность, вписанная в треугольник
Окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. A B C O
A B C D F E M N O K r r r Как вписать в окружность треугольник В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис треугольника. Проведём биссектрисы треугольника: АK, ВM, СN. Построим перпендикуляры ОD, OE, OF, которые равны между собой, т.к. равны соответствующие треугольники. Получаем ОD= OE= OF=r.
Алгоритм построения вписанной окружности в треугольник 1.Строим две биссектрисы треугольника. Точка пересечения — центр вписанной окружности. 2. Строим перпендикуляр на основание из точки пересечения. 3. Этот перпендикуляр является радиусом вписанной окружности. 4. Строим вписанную окружность.
Задача №1 Построить вписанную окружность в: 1. остроугольный треугольник; 2. тупоугольный треугольник; 3. прямоугольный треугольник. Самостоятельная работа Построить вписанную окружность в: 1. остроугольный равнобедренный треугольник; 2. тупоугольный равнобедренный треугольник; 3. прямоугольный равнобедренный треугольник.
Положение центра вписанной окружности
Краткое описание документа:
Презентация по геометрии для урока в 8 классе создана для наглядного изучения вопроса о том, как вписать окружность в треугольник. В ней просто и доходчиво доказывается, что центром окружности, вписанной в треугольник, является точка пересечения биссектрис треугольника. Важная часть презентации — это то, что в ней показан алгоритм построения окружности, вписанной в треугольник. В презентации есть три задачи для закрепления нового материала. Также даны задачи для самостоятельной работы, решение которых поможет ребятам ещё лучше разобраться в новой теме. Последний слайд обращает внимание ребят на положение центра окружности, вписанной в треугольник.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 931 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 309 человек из 67 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 493 719 материалов в базе
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Дистанционные курсы для педагогов
Другие материалы
- 13.05.2015
- 3537
- 13.05.2015
- 764
- 13.05.2015
- 601
- 13.05.2015
- 3372
- 13.05.2015
- 1210
- 13.05.2015
- 621
- 13.05.2015
- 701
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 13.05.2015 6285 —> —> —> —>
- PPTX 227.7 кбайт —> —>
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Сазонова Татьяна Фёдоровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет
- Подписчики: 0
- Всего просмотров: 30277
- Всего материалов: 17
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Построить описанную окружность (Задача 1)Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
В России утвердили новые правила аккредитации образовательных учреждений
Время чтения: 1 минута
В России могут создать комиссию по поддержке одаренных детей
Время чтения: 1 минута
WWF выпустил настольную игру об изменении климата
Время чтения: 3 минуты
В Петербурге дали рекомендации по переводу школьников на дистант
Время чтения: 3 минуты
Школы Сургута переведут на дистанционное обучение с 24 января
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Построить окружность, описанную около треугольникаСкачать

Как построить вписанную окружность треугольника
Видео:Построить окружность, вписанную в треугольникСкачать

Окружность, вписанная в треугольник. Теоремы и их рассмотрение
Еще в Древнем Египте появилась наука, с помощью которой можно было измерять объемы, площади и другие величины. Толчком к этому послужило строительство пирамид. Оно предполагало значительное число сложных расчетов. И кроме строительства, было важно правильно измерить землю. Отсюда и появилась наука «геометрия» от греческих слов «геос» — земля и «метрио» — измеряю.
Исследованию геометрических форм способствовало наблюдение астрономических явлений. И уже в 17-м веке до н. э. были найдены начальные способы расчета площади круга, объема шара и главнейшее открытие — теорема Пифагора.

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:
В треугольник можно вписать только одну окружность.
При таком расположении окружность — вписанная, а треугольник — описанный около окружности.
Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:
Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.
Видео:Построение окружности, вписанной в треугольникСкачать

Окружность, вписанная в равнобедренный треугольник
Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.
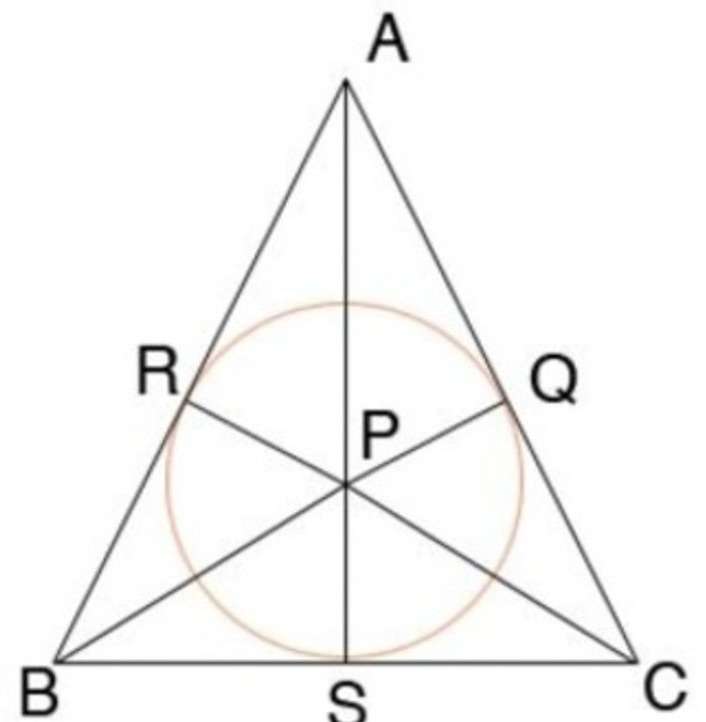
На фото ниже показана окружность, находящаяся внутри равнобедренного треугольника. Условие теоремы об окружности, вписанной в треугольник, соблюдено — она касается всех сторон треугольника AB, ВС И СА в точках R, S, Q соответственно.
Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).
Свойства теоремы об окружности, вписанной в треугольник:
- Отрезки, выходящие из одной вершины треугольника к точкам касания с окружностью, равны. На рисунке AR = AQ, BR = BS, CS = CQ.
- Радиус окружности (вписанной) — это площадь, деленная на полупериметр треугольника. Как пример, нужно начертить равнобедренный треугольник с теми же буквенными обозначениями, что на картинке, следующих размеров: основание ВС = 3 см, высота AS = 2 см, стороны АВ=ВС, соответственно, получаются по 2,5 см каждая. Проведем из каждого угла биссектрису и место их пересечения обозначим как Р. Впишем окружность с радиусом PS, длину которого нужно найти. Узнать площадь треугольника можно, умножив 1/2 основания на высоту: S = 1/2 * DC * AS = 1/2 * 3 * 2 = 3 см2. Полупериметр треугольника равен 1/2 суммы всех сторон: Р = (АВ + ВС + СА) / 2 = (2,5 + 3 + 2,5) / 2 = 4 см; PS = S/P = 3/4 = 0,75 см2, что полностью соответствует действительности, если измерить линейкой. Соответственно, верно свойство теоремы об окружности, вписанной в треугольник.
Видео:7 класс Построение окружности, вписаной в треугольникСкачать

Окружность, вписанная в прямоугольный треугольник
Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.
Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.
Есть хорошая формула, которая поможет высчитать площадь треугольника — периметр умножить на радиус вписанной в этот треугольник окружности.
Видео:Окружность, вписанная в треугольникСкачать

Формулировка теоремы о вписанной окружности
В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:
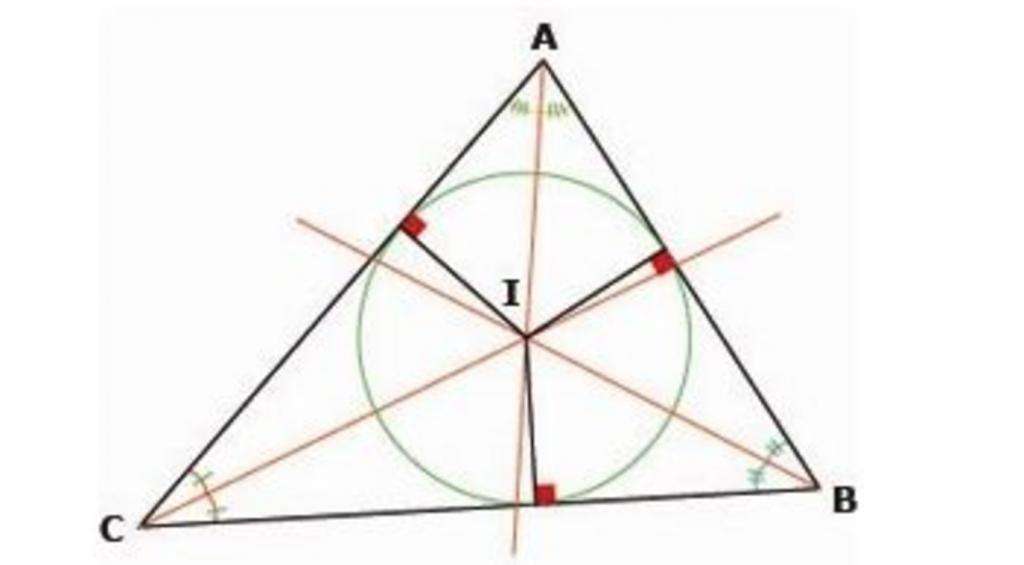
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.
На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Теорема о центре окружности, вписанной в треугольник
Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.
Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.
Видео:№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать

Окружность, вписанная в треугольник
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Видео:Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 классСкачать

Дистанционные курсы для педагогов
Описание презентации по отдельным слайдам:
Окружность, вписанная в треугольник
Окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. A B C O
A B C D F E M N O K r r r Как вписать в окружность треугольник В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис треугольника. Проведём биссектрисы треугольника: АK, ВM, СN. Построим перпендикуляры ОD, OE, OF, которые равны между собой, т.к. равны соответствующие треугольники. Получаем ОD= OE= OF=r.
Алгоритм построения вписанной окружности в треугольник 1.Строим две биссектрисы треугольника. Точка пересечения — центр вписанной окружности. 2. Строим перпендикуляр на основание из точки пересечения. 3. Этот перпендикуляр является радиусом вписанной окружности. 4. Строим вписанную окружность.
Задача №1 Построить вписанную окружность в: 1. остроугольный треугольник; 2. тупоугольный треугольник; 3. прямоугольный треугольник. Самостоятельная работа Построить вписанную окружность в: 1. остроугольный равнобедренный треугольник; 2. тупоугольный равнобедренный треугольник; 3. прямоугольный равнобедренный треугольник.
Положение центра вписанной окружности
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 930 человек из 80 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 323 человека из 72 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 702 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Презентация по геометрии для урока в 8 классе создана для наглядного изучения вопроса о том, как вписать окружность в треугольник. В ней просто и доходчиво доказывается, что центром окружности, вписанной в треугольник, является точка пересечения биссектрис треугольника. Важная часть презентации — это то, что в ней показан алгоритм построения окружности, вписанной в треугольник. В презентации есть три задачи для закрепления нового материала. Также даны задачи для самостоятельной работы, решение которых поможет ребятам ещё лучше разобраться в новой теме. Последний слайд обращает внимание ребят на положение центра окружности, вписанной в треугольник.
- Сазонова Татьяна ФёдоровнаНаписать 6155 13.05.2015
Номер материала: 278228
- 13.05.2015 3072
- 13.05.2015 653
- 13.05.2015 508
- 13.05.2015 2285
- 13.05.2015 1059
- 13.05.2015 499
- 13.05.2015 543
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Построение окружности, вписанной в треугольникСкачать

Дистанционные курсы
для педагогов
530 курсов от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Первый мониторинг вузов РФ по новым показателям пройдёт в 2023 году
Время чтения: 2 минуты
Федеральный перечень учебников будет дополнен новыми учебниками
Время чтения: 3 минуты
Более половины россиян сталкиваются с конфликтами в родительских чатах
Время чтения: 2 минуты
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Ретроспектива культовой сказки «Вечера на Хуторе близ Диканьки»
Время чтения: 5 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
 Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
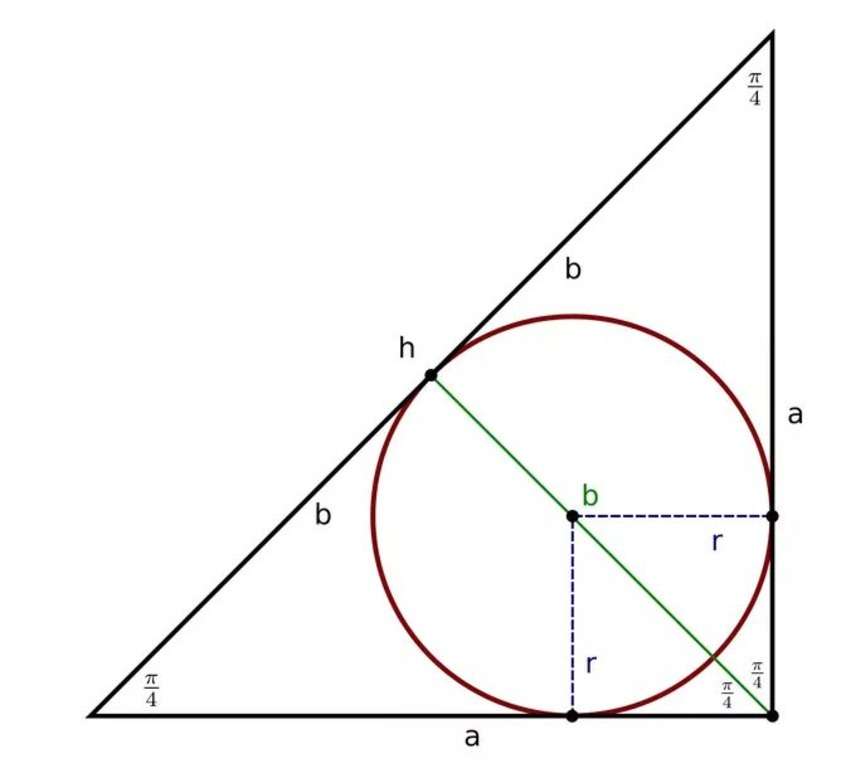
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Окружность, вписанная в треугольникСкачать
Построение с помощью циркуля и линейки — описание, алгоритмы и задачи
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Видео:РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Построение отрезка, равного данному
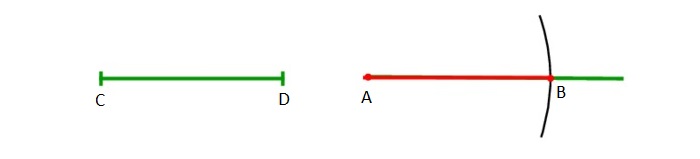
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Деление отрезка пополам
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
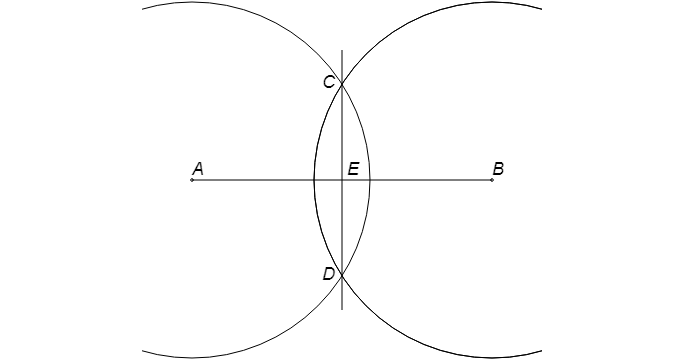
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
Имеется угол ABC.
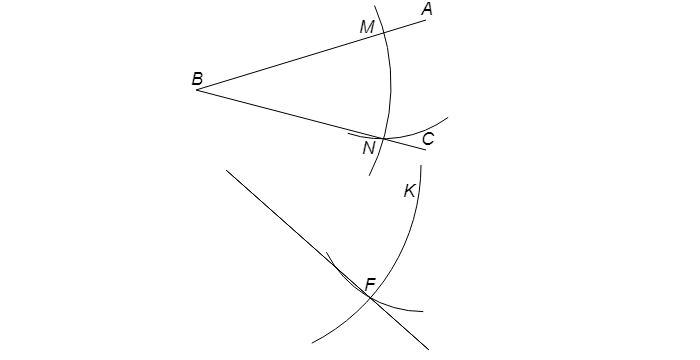
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
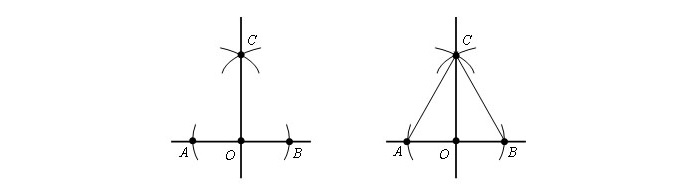
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
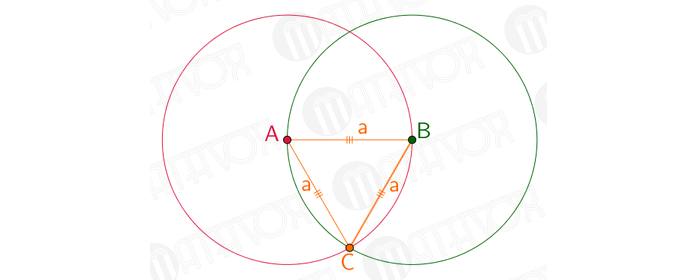
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
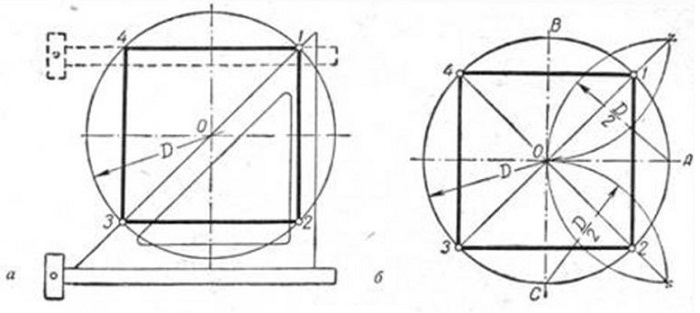
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
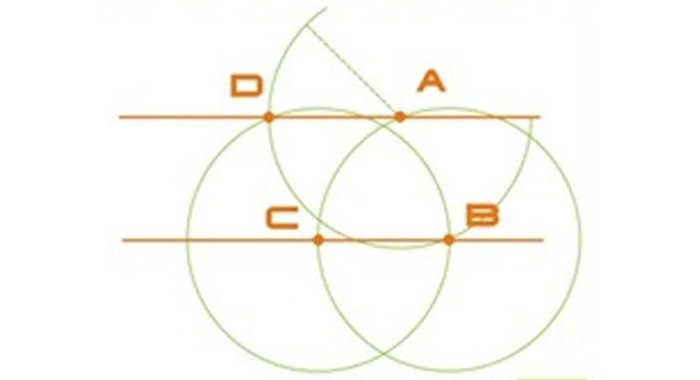
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
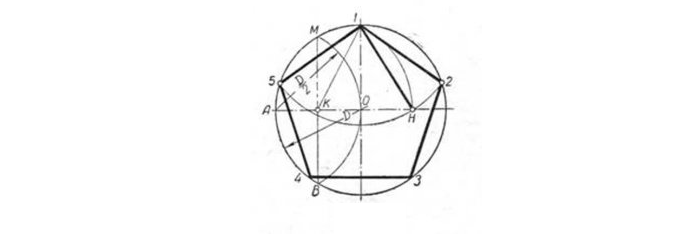
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
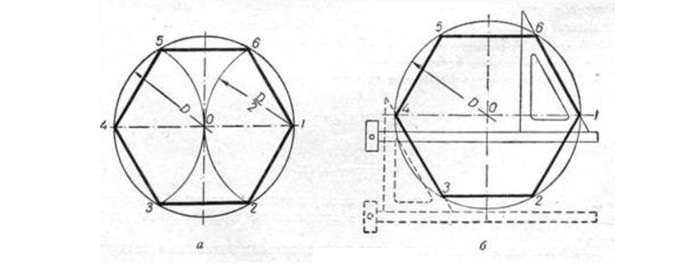
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.