Теорема биссектрисы равнобедренного треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы равнобедренного треугольника (внутренней и внешней), а также разберем пример решения задачи по данной теме.

Примечание: напомним, что равнобедренным называется треугольник, в котором две стороны равны (боковые), а третья является основание фигуры.

Видео:Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Свойства биссектрисы равнобедренного треугольника

Свойство 1

В равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.

• AB = BC, т.к. являются боковыми сторонами равнобедренного △ABC;
• AF = CG, т.к. это биссектрисы, проведенные к боковым сторонам треугольника (или биссектрисы углов BAC и ACB, которые также равны между собой).

Обратная формулировка: если две из трех биссектрис в треугольнике равны, значит он является равнобедренным.

Свойство 2

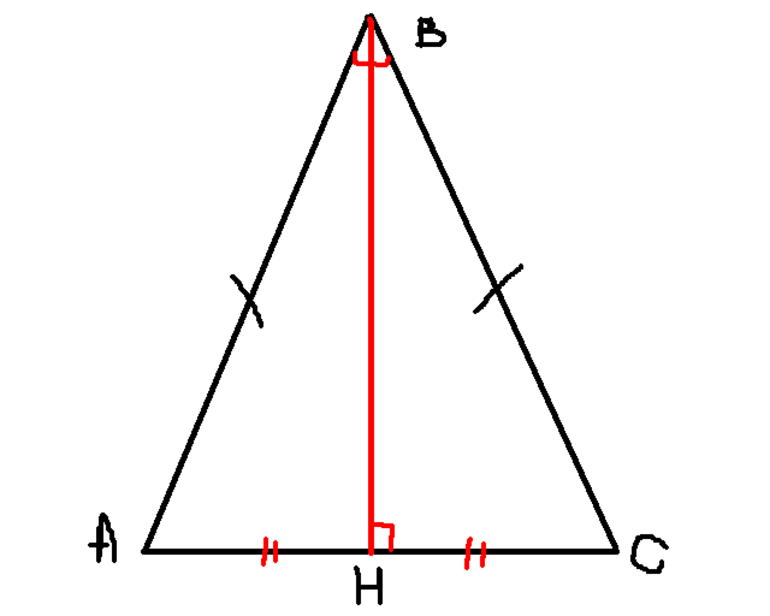
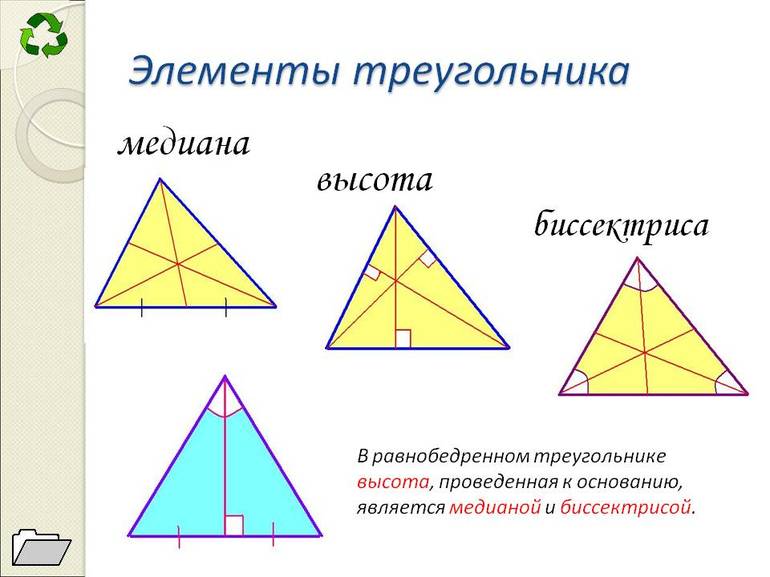
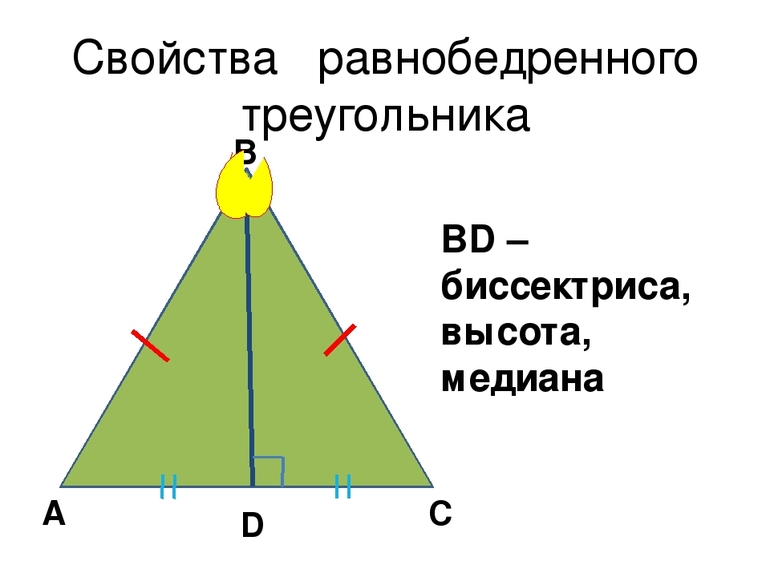
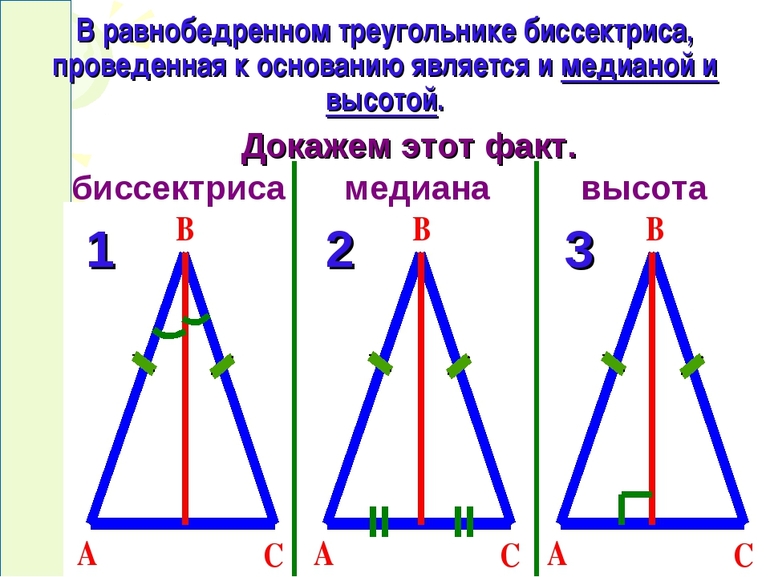
В равнобедренном треугольнике биссектриса, проведенная к основанию, одновременно является и медианой и высотой.

• BH – биссектриса угла ABC, проведенная к основанию AC;
• BH – медиана, значит она делит AC пополам, т.е. AH = HC;
• BH – высота, следовательно, она перпендикулярна AC.

Свойство 3

Если известны стороны равнобедренного треугольника, то длину биссектрисы, проведенную к основанию, можно посчитать по формуле:

Примечание: данная формула следует из теоремы Пифагора ( l и a – катеты прямоугольного треугольника, b – его гипотенуза).

Свойство 4

Внешняя биссектриса угла равнобедренного треугольника, расположенного напротив его основания, параллельна этому основанию.

• BD – внешняя биссектриса ∠ABC треугольника;
• BD параллельна основанию AC.

Примечание: к равнобедренному треугольнику применимы и другие свойства биссектрисы, приведенные в нашей публикации – “Определение и свойства биссектрисы угла треугольника”.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Пример задачи

Биссектриса равнобедренного треугольника с боковой стороной 25 см равняется 20 см. Найдите периметр фигуры.

Решение
Воспользуемся формулой, приведенной в Свойстве 3, чтобы найти длину основания.
a 2 = b 2 – l 2 = 25 2 – 20 2 = 225 .

Извлекаем квадратный корень из найденного значения и получаем 15 см.
Следовательно, основание треугольника равно 30 см (15 см ⋅ 2).

Периметр фигуры равен сумме всех ее сторон, т.е.: 25 см + 25 см + 30 см = 80 см.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Биссектриса в равнобедренном треугольнике — свойства, теоремы и формулы

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Общие сведения

Геометрическая фигура является треугольником, если она состоит из трех точек, лежащих в одной плоскости и не лежащих на одной прямой. Она изучается в пятом классе. В геометрии принято сокращенное обозначение при помощи символа Δ, после которого следует писать произвольные три литеры (вершины) в алфавитном порядке. Например, ТUV.

Вершина — точка, из которой исходят два отрезка и образуют две стороны. Отрезок является элементом луча. Обозначается он двумя заглавными литерами (ТU, UV и т. д. ). Луч — часть прямой, имеющая только начало. Он необходим для построения отрезков, из которых состоят все фигуры геометрии.

Прямая — линия, проходящая в бесконечном пространстве. У нее не существует начала и конца. Математики обозначают ее произвольной маленькой латинской буквой (например, m). Кроме того, у равнобедренного Δ существуют и дополнительные параметры — биссектриса, медиана и высота. Первая делит любой угол (сокращенное обозначение — ∠) при вершине, из которой она исходит, на два ∠ с эквивалентной градусной мерой, т. е. пополам.

Медиана соединяет вершину и середину противоположной стороны, а высота — простой перпендикуляр. Он начинается в вершине и находится внутри треугольника, опускаясь на противолежащую сторону.

Равнобедренный Δ — фигура, имеющая две равные боковые стороны. Следует отметить, что любая биссектриса равнобедренного треугольника является медианой. Это правило выполняется, когда она проведена к основанию фигуры. Существует еще один вид Δ. Он называется правильным или равносторонним. Для него справедливо такое утверждение, сформулированное учеными-математиками: любая высота является медианой и биссектрисой. Для решения задач по геометрии рекомендуется знать теорему о биссектрисе равнобедренного треугольника и ее свойства.

Видео:Теорема о свойстве медианы равнобедренного треугольникаСкачать

Теоремы о биссектрисах

Теорема о биссектрисах треугольника звучит таким образом: точка пересечения биссектрис — инцентр ΔTUV. Доказывается теорема по такому алгоритму:

1. Из вершин T и U нужно провести биссектрисы TT’ и UU’ на противоположные стороны UV и TV соответственно.
2. На чертеже видно, что они пересекаются в некоторой точке. Последнюю следует обозначить Z.
3. Если предположить, что TT’ и UU’ не пересекаются, а параллельны (||), то секущей является сторона TU. В этом случае должно выполняться тождество: ∠(Т/2)+∠(U/2)=180.
4. Однако утверждение в третьем пункте противоречит сумме градусных мер ∠ треугольника, поскольку ∠Т+∠U+∠V=180. Из выражения, полученного на третьем шаге алгоритма, следует, что ∠Т+∠U=360.
5. На основании рассуждений можно сделать вывод, что Z — точка пересечения биссектрис.
6. Таким же образом доказывается случай для вершины V и биссектрисы VV’.
7. Точка Z — центр описанной окружности. Чтобы это доказать, нужно просто провести круг. На рисунке все вершины ΔTUV будут лежать на нем. Теорема полностью доказана.

Кроме того, существует еще одно утверждение, имеющее такой вид: любая высота равнобедренного треугольника является его биссектрисой и медианой.

Доказать его можно посредством такой методики:

1. Начертить равнобедренный ΔTUV. У него стороны TU=UV, а TV — основание.
2. Провести высоту UU’ на основание.
3. Рассмотреть два прямоугольный Δ: TUU’ и UVU’. Они равны между собой, поскольку UU’ — общая, TU=UV и углы (∠Т=∠V) при основании — по определению равнобедренного Δ, а ∠ТU’U=∠UU’V — по построению.
4. На основании третьего пункта можно сделать вывод о равенстве сторон TU’ и VU’, а также ∠U’UТ=∠VU’U. Следовательно, в первом случае UU’ — медиана, а во втором — биссектриса.
5. На основании четвертого утверждения теорема доказана.

Кроме того, существуют определенные свойства, которые могут быть полезными при решении задач. Их получают из теорем и других тождеств, доказываемые математиками.

Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Полезные свойства

Математики вывели пять полезных свойств для биссектрисы в равнобедренном Δ.

К ним относятся следующие:

1. Свойство биссектрисы, проведенной к основанию равнобедренного треугольника: она есть медиана и высота.
2. При проведении из вершин, образующих основание, углы, образованные ими, эквивалентны между собой.
3. Если провести биссектрису TT’ из вершины при основании, то будет выполняться следующее тождество: TU/TV=UT’/T’V (отношение стороны к основанию эквивалентно частному из двух отрезков, полученных при построении).
4. Длина биссектрисы, проведенной к основанию, эквивалентна корню второй степени из квадрата боковой стороны без четвертой части квадрата основания: UU’=[m 2 — (¼)*n 2 ](^½), где m и n — длина боковой стороны и основания.
5. Через точку пересечения проходит круг, касающийся вершин основания.

Следует отметить, что в равностороннем треугольнике каждая биссектриса будет отсекать равные углы из каждой вершины.

В нем можно провести их всего три, а в равнобедренном — 2 высоты, 2 медианы, 2 биссектрисы, а также одну к основанию.

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Пример решения

Чтобы усвоить материал, необходимо решить задачу по геометрии. Ее условие имеет такой вид:

1. Периметр равнобедренного Δ равен 40 см.
2. Основание больше боковой стороны на 10 см.

Необходимо найти значение высоты. Решать нужно по такому алгоритму:

1. Составить уравнение: 40=2*t+(t+10), где t — боковая сторона, а (t+10) — основание.
2. Раскрыть скобки: 40=2*t+t+10.
3. Привести подобные коэффициенты:3t=30.
4. Найти неизвестную: t=10 (см).
5. Вычислить основание: 10+10=20 (см).
6. Определить высоту: h= [100+((¼)*20)^2]^(½)=5[5]^(½) (см).

Следовательно, высота равнобедренного Δ со сторонами 10 и 20 см эквивалентна 5[5]^(½) см. Существуют и более сложные задачи, в которых требуется составлять уравнения. Например, условие одной из них имеет такой вид:

1. Высота, опущенная из вершины на основание (ТТ’), равна 20 см.
2. Основание больше стороны на 5 см.

Необходимо найти периметр треугольника. Для решения задачи необходимо составить определенный алгоритм:

1. Обозначить стороны: основание — n, сторона — m и высота — h.
2. Периметр P: Р=2m+n.
3. Записать формулу, руководствуясь первым и четвертым свойствами биссектрисы: h=[m 2 -(¼)*n 2 ]^(½).
4. Записать связь сторон, обозначив боковую сторону переменной t: t=t+5.
5. Подставить в соотношение во втором пункте: 20=[t 2 -(¼)*(t+5)^2]^(½).
6. Возвести обе части в квадрат: 400=t 2 -(¼)*(t+5)^2.
7. Раскрыть скобки: 400=t 2 -(¼)*(t 2 +10+25)=t 2 -(¼)t 2 −10/4−25/4=(¾)t 2 -(10/4)-25/4=(¼)*(3t 2 -10−25).
8. Решить квадратное уравнение, сократив на ¼ обе части: (3t 2 -10t-25)=200.
9. Первый корень равен -7, а второй — +25. Второе значение подходит, поскольку является положительным числом.
10. Основание вычисляется таким образом: n=25+5=30 (см).
11. Если подставить полученное значение для проверки в соотношение h=[t 2 -(¼)*(t+5)^2]^(½), то получится такое выражение: 20=[25 2 -(¼)*30 2 ]^(½)=[625−900/4]^(½)=[625−225]^(½)=20. Значение найдено верно.
12. Периметр находится по формуле: P=25*2+30=80 (см).

Задача решена в полном объеме. Из методики решения видно, что сначала нужно записать основную формулу, а затем найти неизвестные в ней величины по другим вспомогательным тождествам.

Таким образом, при решении задач по геометрии необходимо знать основные определения, формулы, свойства и теоремы, которые также могут быть полезны.

Видео:Свойство биссектрисы равнобедренного треугольникаСкачать

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:№133. Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольникСкачать

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

💥 Видео

Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Каждая из биссектрис равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Биссектриса равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

№233. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника,Скачать

Свойство биссектрисы равнобедренного треугольника. ЗадачаСкачать

Биссектриса равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

ПОМОГИТЕ ДОКАЗАТЬ Если две биссектрисы равны, то треугольник равнобедренныйСкачать

Доказательство свойства биссектрисы равнобедренного треугольника.Скачать