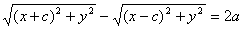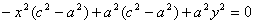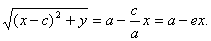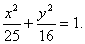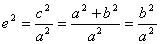Сжатие окружности в эллипс (6 видео) | Курс школьной геометрии

Сжатие окружности в эллипс

Пусть, наконец, из точки P проведены к эллипсу две взаимно перпендикулярные касательные t₁ и t₂ (см. Рис. 17).

Отразим фокус относительно прямой t₂ и полученную точку соединим с F. Очевидно, что и угол — прямой (последнее следует из того, что угол между t₁ и t₂ прямой, и второй теоремы Понселе); следовательно . Но ; поэтому . С другой стороны, PO — медиана треугольника , так что . Учитывая предыдущее равенство получаем: PO 2 = 2a 2 — c 2 или PO 2 = (a 2 — c 2 ) + a 2 = a 2 + b 2 , т. е. вершины прямых углов, стороны которых касаются эллипса, расположены на окружности радиуса с центром в центре эллипса.

Эллипс как результат сжатия окружности. Пусть точка M, принадлежащая эллипсу, удалена от главной оси x на расстояние MM₁ = y, а от главной оси y — на расстояние MM₂ = x (см. Рис. 18). Симметрия эллипса позволяет ограничиться рассмотрением точек эллипса, расположенных внутри одного из прямых углов, образованных главными осями x и y. Из соотношений (2) следует:

После исключения r и d, получим:

откуда, умножая обе части равенства на a и учитывая соотношения (2), найдем окончательно:

(3)

Содержание

Эллипс
Сжатие окружности в эллипс
В окружности ( x – a ) 2 + ( y – b ) 2 = R 2 центр имеет координаты ( a ; b ).
💥 Видео

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Эллипс

Изобразим окружность, заданную, например, уравнением х 2 + у 2 = 16 (рис. 3.18).

Деформируем окружность, подвергнув ее равномерному сжатию вдоль оси Оу в два раза. В результате сжатия окружности получается новая линия, которая называется эллипсом (рис. 3.19).

При указанном сжатии каждая точка М(х; у) окружности переместится по вертикали в точку эллипса М(х; у) так, что при одинаковых абсциссах х ординаты точек М и М связаны соотношением:

Подставив это выражение в уравнение окружности, получаем соотношение, связывающее координаты точек эллипса:

или после деления обеих частей на 16 имеем:

Отбрасывая тильду (волну «

»), т.е. обозначая в дальнейшем координаты произвольной точки эллипса х и у, получаем каноническое уравнение эллипса:

Разумеется, любую окружность радиуса а (с уравнением х 2 + у 2 = а 2 ) можно подвергнуть аналогичному сжатию (и не обязательно в два раза). При этом получается эллипс (изображенный на рис. 3.20), каноническое уравнение которого имеет вид:

Перечислим свойства эллипса.

1. Эллипс располагается в прямоугольнике, ограниченном прямыми: х = а_> х = -а, у = Ь, у = -Ь.
2. Оси координат являются осями симметрии эллипса.
3. Начало координат — центр симметрии эллипса. Эллипс — центральная кривая второго порядка.

4. Отрезок, соединяющий две точки эллипса, симметричные относительно центра, называется диаметром эллипса. Все диаметры эллипса проходят через его центр, в котором каждый из них делится пополам. В рассматриваемом случае при а > Ь, горизонтальный диаметр М_<М₂ — наибольший, а вертикальный М_лМ_{/ <}— наименьший. Концы этих двух диаметров называются вершинами эллипса; координаты вершин: М_х(-а 0), М₂(а; 0), М₃(0; —b), М₄(0; b).
5. Расстояние от вершины до центра называется полуосью. Эллипс имеет две полуоси: большую, равную а, и малую, равную Ь.
6. На рис. 3.20 на горизонтальном диаметре эллипса

отмечены две точки F_x(-c; 0) и F₂(c; 0) (где с = 1а-Ь ), которые называются фокусами эллипса; с фокусами связано замечательное (определяющее) свойство эллипса: сумма расстояний от любой точки эллипса до его фокусов равна 2а.

7. Окружность является частным случаем эллипса (при b = а). То есть окружность — это эллипс, у которого большая и малая полуоси равны между собой. В этом случае фокусы совпадают с центром.

Замечание. Эллипсы имеют важные приложения в физике и астрономии.

Физическое свойство фокусов: если в один из фокусов помещен точечный источник света, то отразившись от эллиптического зеркала, все лучи соберутся во втором фокусе.

В астрономии мы встречаемся с эллипсом в первом законе Кеплера: «Каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце».

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Сжатие окружности в эллипс

Ах 2 + 2Вху + Су 2 + 2 Dx + 2 Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) — уравнение эллипса.

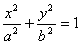
2) — уравнение “мнимого” эллипса.

3) — уравнение гиперболы.

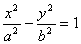
4) a 2 x 2 – c 2 y 2 = 0 – уравнение двух пересекающихся прямых.

5) y 2 = 2 px – уравнение параболы.

6) y 2 – a 2 = 0 – уравнение двух параллельных прямых.

7) y 2 + a 2 = 0 – уравнение двух “мнимых” параллельных прямых.

8) y 2 = 0 – пара совпадающих прямых.

9) ( x – a ) 2 + ( y – b ) 2 = R 2 – уравнение окружности.

В окружности ( x – a ) 2 + ( y – b ) 2 = R 2 центр имеет координаты ( a ; b ).

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2 x 2 + 2 y 2 – 8 x + 5 y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x 2 + y 2 – 4 x + 2,5 y – 2 = 0

x 2 – 4 x + 4 –4 + y 2 + 2,5 y + 25/16 – 25/16 – 2 = 0

( x – 2) 2 + ( y + 5/4) 2 – 25/16 – 6 = 0

( x – 2) 2 + ( y + 5/4) 2 = 121/16

Отсюда находим О (2; -5/4); R = 11/4.

Определение. Эллипсом называется линия, заданная уравнением .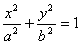

О пределение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:

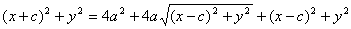
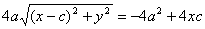
Доказательство: В случае , если точка М находится на пересечении эллипса с вертикальной осью, r ₁ + r ₂ = 2 (по теореме Пифагора). В случае , если точка М находится на пересечении эллипса с горизонтальной осью, r ₁ + r ₂ = a – c + a + c . Т.к. по определению сумма r ₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

a 2 = b 2 + c 2

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Определение. Величина k = b / a называется коэффициентом сжатия эллипса, а величина 1 – k = ( a – b )/ a называется сжатием эллипса.

Коэффициент сжатия и эксцентриситет связаны соотношением: k 2 = 1 – e 2 .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

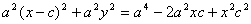
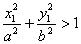
Если для точки М( х₁, у₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

Теорема. Для произвольной точки М( х , у), принадлежащей эллипсу верны соотношения:

r ₁ = a – ex , r ₂ = a + ex .

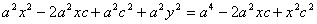
Доказательство. Выше было показано, что r ₁ + r ₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r ₂ = a + ex . Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

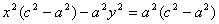
x = a / e ; x = — a / e .

Теорема. Для того , чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:

1) Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

2) Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F ₂ (-3; 0).

3) Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение эллипса, если его фокусы F ₁ (0; 0), F ₂ (1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: 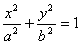. Расстояние между фокусами:

2 c = , таким образом, a 2 – b 2 = c 2 = ½

по условию 2а = 2, следовательно а = 1, b =

Итого: .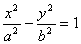

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

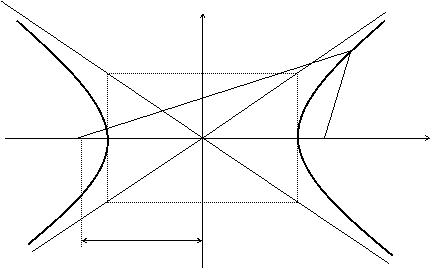
По определению ï r ₁ – r ₂ ï = 2 a . F ₁ , F ₂ – фокусы гиперболы. F ₁ F ₂ = 2 c .

Выберем на гиперболе произвольную точку М( х , у). Тогда :

обозначим с 2 – а 2 = b 2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2 b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых

Определение. Отношение 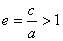называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с 2 – а 2 = b 2 :

Если а = b , e = , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a / e от него, называются директрисами гиперболы. Их уравнения: .

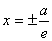
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого — либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.