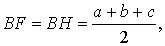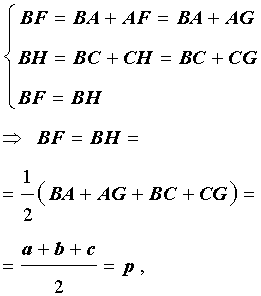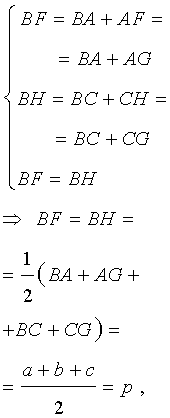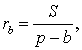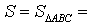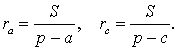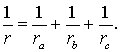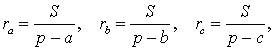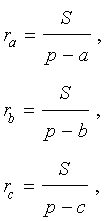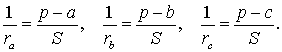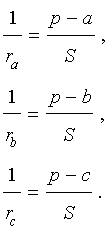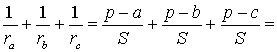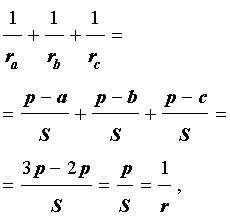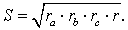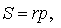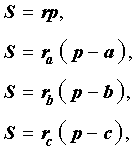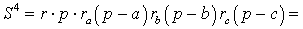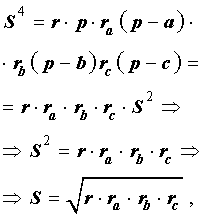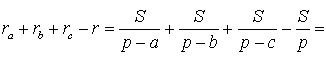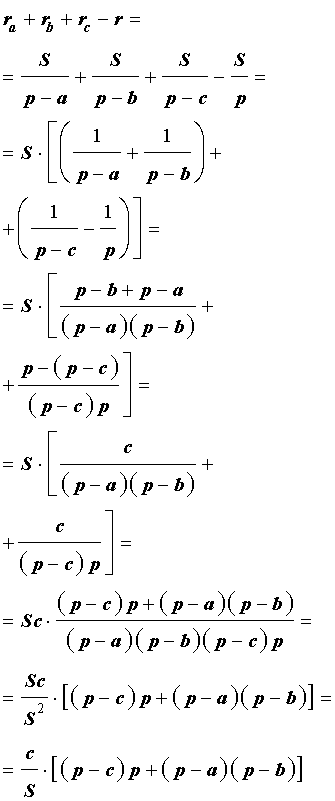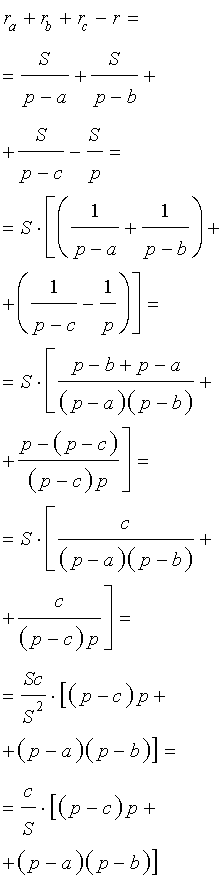Свойства вневписанной окружности с доказательством (6 видео)

Вневписанные окружности

Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

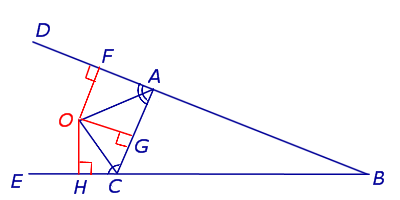
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

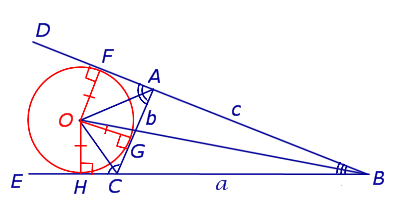
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом r_b .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

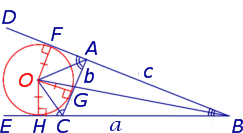
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

Следовательно, справедливо равенство

что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

Доказательство . Перемножим формулы

что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

Преобразуем выражение, стоящее в квадратной скобке:

Содержание

Вневписанная окружность треугольника.
Вневписанная окружность
Скачать:
Предварительный просмотр:
🎦 Видео

Видео:Вневписанная окружностьСкачать

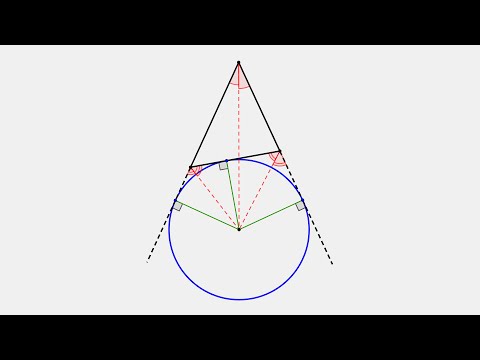
Вневписанная окружность треугольника.

Определение.

Окружность, касающаяся стороны треугольника и продолжения двух других его сторон, называется вневписанной окружностью треугольника.

Теорема 1.

Центр окружности, вневписанной в треугольник, есть точка пересечения биссектрис двух внешних и одного внутреннего угла треугольника.

Доказательство.

BF — биссектриса ∠JBG, следовательно F равноудалена от сторон данного угла.

СF — биссектриса ∠JСH, следовательно F равноудалена от сторон данного угла.

Следовательно, точка F равноудалена от сторон ∠BAC.

Таким образом, точка F — центр окружности, касающейся стороны BC и продолжения сторон AB и AC. По определению данная окружность называется вневписанной окружностью треугольника.

Теорема 2.

Отрезок, соединяющий вершину треугольника с точкой касания вневписанной окружности и противолежащей стороны, делит треугольник на два треугольника равного периметра.

Доказательство.

BJ=BG, GC=CH и AJ=AH (свойство отрезков касательных, проведенных из одной точки к окружности).

P_ΔABC=AB+ BC +AC=AB+ BG + GC +AC=AB+ BJ + AC +CH=AJ+AH.

Так как AJ=AH, то P_ΔABC/2=AJ=AH и P_ΔABC/2+AG=AJ+AG=AH+AG=AB+BG+GA=AC+CG+GA.

Следовательно, отрезок AG поделил треугольник ABC на два треугольника равного периметра P_ΔABC/2+AG.

Видео:Вневписанная окружность. Теория | Профильная математика в онлайн - школе СОТКАСкачать

Вневписанная окружность

Чем же геометрия выделяется среди других разделов математики? Прежде всего, геометрия, наверное, самая древняя наука. Более того сам термин «математика» возник сравнительно недавно, так что ученые древности и отчасти средневековья, занимавшиеся в нашем понимании математикой, называли себя геометрами. Некоторые теоремы геометрии являются одними из древнейших памятников мировой культуры. Они старше самой Библии.

Один мудрец сказал: «Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою».

Моя работа посвящается одному из интереснейших понятий геометрии, которое обычно остаётся в стороне от выбранного нами пути построения геометрической теории.

Во-первых, речь пойдёт о треугольнике. За этой, казалось бы, простейшей геометрической фигурой, скрывается богатый мир.

В своём учебнике геометрии Игорь Фёдорович Шарыгин написал: «каждый треугольник определяет семейство окружностей, помогающих глубже и полнее понять «устройство» треугольника»

Рассмотрим одно из таких «семейств». Оказывается, что у каждого треугольника имеется четыре окружности, касающиеся всех трех прямых, образующих этот треугольник. Одна из них — это известная вам вписанная окружность. Три другие называются вневписанными окружностями.

Видео:Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Скачать:

Вложение	Размер
исследователькая работа по геометрии	673.5 КБ
vnevpisannaya_okruzhnost.ppt	899.5 КБ

Видео:✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

Предварительный просмотр:

Министерство образования и науки Российской Федерации.

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

КИРОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА.

Адрес: 347789, Ростовская область, Веселовский район, п. Средний Маныч,

ул. Просвещения 22А, тел. (8 633) 69 4 43.

исследовательский проект на тему :

Выполнила: ученица 9 класса

МБОУ КИРОВСКАЯ СОШ

Маломагомедова Людмила Султанбеговна

Руководитель: учитель математики

МБОУ КИРОВСКАЯ СОШ

Качула Наталья Николаевна.

п. Средний Маныч

Содержание

Введение 2
Вневписанная окружность и её свойства 3

2.1 Определение вневписанной окружности
2.2 Свойства вневписанной окружности

Вневписанная окружность в задачах 10

3.1 Задачи на доказательство……………………………………10
3.2 Задачи на построение………………………………………… 12
3.3 Задачи на вычисление………………………………………… 13

Задачи ГИА и ЕГЭ на применение свойств вневписанных окружностей 16
Заключение 19
Список использованной литературы 20

1. Ввести определение вневписанной окружности треугольника.

2. Рассмотреть свойства вневписанных окружностей треугольника.

3. Показать применение свойств вневписанной окружности при решении задач на доказательство, построение и вычисление.

Актуальность исследования: Показать практическую направленность науки геометрии

метод теоретического анализа учебной литературы;
метод обобщения справочных и познавательных материалов первоисточников;
практическое применение при решении задач ГИА и ЕГЭ.

2. Вневписанная окружность и её свойства.

2.1 Определение вневписанной окружности.

Рассмотрим треугольник АВС . Продолжим его стороны за точки В и С. Проведём биссектрисы внешних углов В и С. Они пересекутся в точке Ка. Эта точка равноудалена от лучей АВ и ВС и от лучей АС и СВ. Значит, Ка равноудалена от всех трех прямых АВ, ВС и СА, поэтому существует окружность с центром в точке Ка, касающаяся стороны ВС и продолжений сторон АВ и АС. Расстояния от Ка до ВС, ВК 1 и СК 2 — это радиусы построенной окружности. Заметим, что через Ка проходит и биссектриса угла А треугольника АВС

Аналогично можно построить окружности, касающиеся двух других сторон. Всего у треугольника имеется три вневписанных окружности.

Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.

2.2 Свойства вневписанной окружности.

Выясним, как связаны радиусы вневписанных окружностей с другими элементами треугольника.

Свойство 1.Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника (1)

Дано:

М, N, К – точки касания

Т. к. окружность касается сторон угла САК, то центр окружности О равноудален от сторон этого угла, следовательно, он лежит на биссектрисе угла САК. Аналогично, точка О лежит на биссектрисе угла АСN. Т. к. окружность касается прямых ВА и ВС, то она вписана в угол АВС, а значит её центр лежит на биссектрисе угла АВС. Ч.т. д.

Свойство 2.Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника
АВ 1 = АС 1 = p

∆АВС , Вневписанная окр. (О а ; r a )

Доказать, что АВ 1 = АС 1 = p

Т.к. Оа — центр вневписанной окружности. Касательные, проведенные к окружности из

одной точки, равны между собой,

поэтому ВВ 1 = ВА 1 , СА 1 = СС 1 , АВ 1 = АС 1 .

Значит, 2p = (AC + СА 1 ) + (AB + ВА 1 ) = (AC + CC 1 ) + (AB + BB 1 ) = AC 1 + AB 1 = 2AC 1 = 2AB 1. т.е. АВ 1 = АС 1 = p.

Теорема1. Радиус вневписанной окружности, касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е. r a = p·tg , r b = p·tg ,

Теорема 2 . Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. т.е.

r a = , r b = , r c =

Доказательство. Легко видеть, что

Теорема3. Сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра описанной окружности, т. е.

Выразим все радиусы через стороны, площадь и полупериметр треугольника:

r = , R = , r a = , r b = , r c =

r a + r b + r c – r = + + — =

= =

Т.е. r a + r b + r c = r + 4R .

Теорема 4. Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, т. е.

Используем выражения радиусов через стороны и площадь треугольника:

r = , R = , r a = , r b = , r c =

Теорема 5. Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника, т. е.
r a r b + r b r c + r c r a = p 2

Воспользуемся формулами ранее доказанных радиусов через стороны и площадь треугольника:

r = , r a = , r b = , r c =

Из формулы Герона следует

(p – a)(p – b)(p – c) = , поэтому

Теорема 6 . Произведение всех трех радиусов вневписанных окружностей равно произведению радиуса вписанной окружности на квадрат полупериметра треугольника, т.е.
r a r b r c = rp 2

Из ранее доказанных формул для радиусов и формулы Герона

r a = , r b = , r c = ,

Следствие 1 . Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е.

Из r a r b r c = rp 2 = rp × p = Sp.

Следствие 2 . Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е.

Из следствия 1, что и равенства S = pr,

получаем, перемножая их почленно,

Следствие 3. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е.

Вневписанная окружность в задачах

3.1 Задачи на доказательство.

Отметим, что условия следующих задач не содержат термина «вневписанная окружность». Она появляется в решении как вспомогательная фигура.

Задача 1. Из точки А к данной окружности проведены касательные АТ 1 и АТ 2 . К окружности проведена касательная, пересекающая отрезки АТ 1 и АТ 2 в точках ВиС. Докажите, что периметр треугольника ABC не зависит от положения касательной.

Решение. По теореме 2, независимо от положения касательной, периметр треугольника ABC равен удвоенной длине отрезка АТ 1 .

Задача 2. К двум непересекающимся окружностям проведены две общие внешние касательные и общая внутренняя касательная. Докажите, что отрезок внутренней касательной, заключенный между внешними касательными, равен отрезку внешней касательной, заключенному между точками касания.

Решение. Пусть O 1 и O 2 — данные окружности, а точки касания окружностей с первой внешней касательной — А и B , со второй — С и D (рис.4). Пусть также внутренняя касательная пересекает внешние в точках М и N . Продолжим прямые АВ и CD до их пересечения в точке К . Тогда окружность O 2 является вписанной в треугольник MNK , а окружность O 1 — вневписанной. Обозначим сторону MN треугольника MNK через а и его полупериметр через р . Тогда АК = р и ВК = р — а . Значит, АВ = а , т.е. АВ = = MN .

Задача 3. Докажите формулу Герона для площади треугольника:

Решение. Воспользуемся обозначениями данного рисунка. Треугольники CJ a T 1 и СОК подобны. Значит, СТ 1 /r а = r/СК .

Но СК = р — с, а СТ 1 = р-АС = р — b .

Откуда (p-b)/r a = r/(р — c), или rr a = (р-с)(р-b).

Но r a = S/(p-а)(теорема 3), а r = S/p, значит,

Отсюда и следует формула Герона.

Задача 4. Докажите, что прямая, проходящая через середину стороны ВС и точку пересечения биссектрис треугольника ABC, отсекает на высоте, проведенной к стороне ВС, отрезок, равный радиусу вписанной в этот треугольник окружности.

Решение. Обозначим середину стороны ВС через М 1 , центр вписанной окружности через О , а точку пересечения прямой М 1 О с высотой АН 1 через Е . Через точку К 1 касания вписанной окружности со стороной ВС проведем диаметр вписанной окружности K 1 R . По теореме 4 точки А , R и Т 1 лежат на одной прямой. Отрезок СТ 1 равен р — b (см. решение задачи 2). Но и отрезок ВК 1 также равен р — b . Значит, точка М 1 является серединой отрезка Т 1 K 1 . Следовательно, М 1 О — средняя линия треугольника T 1 RK 1 . Значит, М 1 О || RТ 1 . А поскольку АН 1 || RK 1 , то RAEO — параллелограмм. Т.е. отрезок АЕ равен радиусу вписанной окружности, что и требовалось доказать.

Задача 5. Докажите формулу для площади треугольника:

где R — радиус описанной окружности, а p H — полупериметр треугольника, образованного основаниями высот данного треугольника.

Решение. Известно, что углы Н 1 Н 2 Н 3 равны 180° — 2 А, 180° — 2В, 180° — 2С и что высоты треугольника ABC являются биссектрисами углов Н 1 Н 2 Н 3 . Угол ТН 2 Н 3 — смежный с углом H 3 H 2 H 1 , Н 2 В — биссектриса угла Н 3 Н 2 Н 1 , а угол ВН 2 А — прямой; следовательно, Н 2 А — биссектриса угла ТН 2 Н 3 . А значит, точка А — центр вневписанной окружности треугольника Н 1 Н 2 Н 3 . Следовательно, отрезок Н 1 Т равен р H . Из прямоугольного треугольника АН 1 Т имеем:

p H = h a cosAH 1 T = h a cos(90° — A) = h a sin A

где h a — высота к стороне ВС , a — длина стороны ВС, А — величина угла ВАС. Отсюда и следует доказываемая формула S = Rp H .

3.2 Задачи на построение

Задача 1. Внутри угла с вершиной А дана точка М. Через точку М проведите прямую так, чтобы она отсекала треугольник наименьшего периметра.

Решение. Проведем через точку М произвольную прямую, пересекающую стороны угла в точках В и С . Построим вневписанную окружность треугольника ABC , касающуюся прямой АС в точке Т . Тогда периметр треугольника ABC равен 2AT (теорема 2). Для того чтобы построить треугольник с наименьшим периметром, надо прямую ВС провести так, чтобы отрезок AT , а значит и радиус вневписанной окружности, имел наименьшее значение. Это будет тогда, когда вневписанная окружность проходит через точку М . Итак, для построения треугольника с наименьшим периметром необходимо построить окружность, проходящую через точку М и касающуюся сторон угла (это — известная задача, решаемая с помощью гомотетии), затем провести к окружности касательную в точке М . Проведенная касательная — искомая прямая.

Задача 2. Постройте треугольник, если дана сторона, противолежащий ей угол треугольника и сумма двух других сторон.

Решение. Пусть дана сторона a, угол А и сумма сторон b + с. Тогда известна длина полупериметра искомого треугольника р = (а + b + с)/2. Значит, известны положения точек Т 1 и Т 2 на сторонах угла А. Восставив перпендикуляры в этих точках к сторонам угла А, на их пересечении получим центр вневписанной окружности, а значит, вневписанная окружность построена. Расстояние от точки Т 1 до точки касания вписанной окружности равно а. Следовательно, мы можем найти точки касания вписанной окружности искомого треугольника со сторонами угла A и построить саму вписанную окружность. Общая внутренняя касательная к построенным окружностям отсекает на сторонах угла искомый треугольник.

3.3 Задачи на вычисления:

Задача 1. Дан квадрат ABCD со стороной а. На сторонах ВС и CD даны точки М и N такие, что периметр треугольника CMN равен 2а. Найдите угол MAN.

Решение. Расстояния от вершины С треугольника CMN до точек В и D равны его полу периметру. Значит, В и D — точки касания вневписанной окружности, а ее центр находится в вершине А квадрата ABCD. Тогда AM и AN — биссектрисы углов BMN и MND соответственно.

Далее,  CMN +  CNM = 90°, значит,

 AMN +  MNA = 180° — (  CMN +  CNM)/2 = 135°. Откуда

 MAN = 180° — (  AMN +  MNA ) = 45°.

Задача 2 . В прямой угол с вершиной С вписаны две окружности, которые не пересекаются. К этим окружностям проведена общая касательная, которая пересекает угол в точках А и В. Найдите площадь треугольника ABC, если радиусы окружностей равны R 1 и R 2 .

Решение. Отрезок СТ 1 ( Т 1 — точка касания прямой СВ и окружности радиуса R 2 ) равен R 2 . Но окружность радиуса R 2 является вневписанной окружностью треугольника АВС. Значит, СТ 1 — полупериметр треугольника ABC. Его площадь находим как произведение радиуса вписанного круга на полупериметр:

Задача 3. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найдите сторону треугольника, если радиус малой окружности равен r.

Решение. Обозначим через а длину стороны треугольника. Тогда радиус окружности, вписанной в данный треугольник ABC , равен . Проведем общую касательную MN к большому и малому кругам. Очевидно, что MN || АВ. Тогда треугольники MNC и ABC подобны. А значит, отношение радиусов вписанных в них окружностей равно отношению их периметров, т. е.

Задача 4. В треугольнике ABC проведены биссектрисы AL 1 и BL 1 . Найдите угол A, если известно, что L 1 L 2 — биссектриса угла AL 1 C.

Решение. Точка L 2 по условию лежит на пересечении биссектрисы внутреннего угла AВС и биссектрисы внешнего угла AL 1 C треугольника ABL 1 . Значит, точка L 2 является центром вневписанной окружности треугольника ABL 1 . Следовательно, AL 2 — биссектриса внешнего угла А треугольника ABL 1 . Несложно заметить, что в этом случае угол А равен 120°.