Окружность называется вписанной в угол, если она касается сторон угла.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

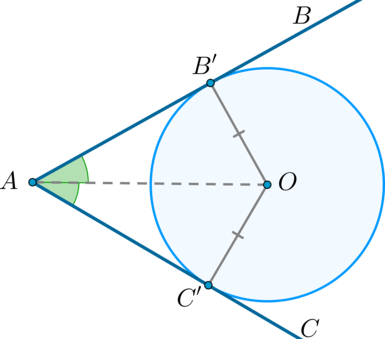
окружность (O; R) вписана в угол ABC, O∈BD
Доказать : BD — биссектриса ∠ABD

Значит, прямоугольные треугольники BOF и BOP равны (по катету и гипотенузе).
Из равенства треугольников следует равенство соответствующих углов: ∠FBO=∠PBO.
Следовательно, BO — биссектриса угла ABC.
Что и требовалось доказать.
OF=OP (как радиусы). Значит, точка O равноудалена от сторон угла ABC. А так как любая точка внутри неразвёрнутого угла, равноудалённая от сторон этого угла, лежит на его биссектрисе, то BO — биссектриса угла ABC.
Видео:Углы, вписанные в окружность. 9 класс.Скачать

Справочник репетитора по математике. Свойства окружности и ее элементов
Теоретические справочные материалы по геометрии для выполнения заданий от репетитора по математике. В помощь ученикам при решении задач.
1) Терема о вписанном угле в окружность.


2) Следствия из теоремы о вписанном угле в окружность.
2.1) Свойство углов, опирающихся на одну дугу.

Теорема: если вписанные углы опираются на одну дугу, то они равны (если они опираются на дополнителные дуги, их сумма равна
2.2) Свойство угла, опирающегося на диаметр. 
Теорема: вписанный угол в окружность опирается на диаметр тогда и только тогда, когда он прямой.
AC-диаметр
3) Cвойство отрезков касательных. Окружность, вписанная в угол. 
Теорема 1: если из одной точки, не лежащей на окружности, проведены к ней две касательные, то их отрезки равны, то есть PB=PC.
Теорема 2: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть PO-биссектриса.
4) Свойство отрезков хорд при внутреннем пересечении секущих.



Теорема 2: угол между хордами равен полусумме дуг, которые этими хордами образуются на окружности, то есть
5) Свойство отрезков хорд при внешнем пересечении секущих. 
Теорема 1: произведение отрезков одной секущей равно произведению отрезков другой, то есть


Теорема 2: угол между секущими равен полуразности соответствующих им дуг, то есть
Комментарий репетитора по математике: Обратитте внимание на общую закономерность 4-го и 5-го свойства: хорды в произведениях не участвуют, а сами равенства (с частями и продолжениями хорд) при сохранении обозначений являются точной копией друг друга. Также можно подметить общую структуру равенств с дугами. Репетитору по математике стоит обратить на этих особенностях внимание ученика.
6) Свойства квадрата отрезка касательной 
Теорема 1: Квадрат отрезка касательной равен произведению отрезков секущей, то есть

Теорема 2:угол между касательной и секущей равен полуразности соответствующих им дуг, то есть
7) Угол между касательной и секущей 
Теорема:угол между касательной и секущей, проведенными из одной точки окружности, равен поливине дуги, которую отсекает сукущая (половине центрального угла, соответствующего данной дуге).

Колпаков Александр Николаевич, репетитор по математике.
Уважаемый коллега, ваш материал на сайте является для меня хорошим методическим подспорьем. Спасибо.
Александр Николаевич, спасибо за методики, я восхищена Вашим трудолюбием и профессионализмом.
Уважаемый Александр Николаевич! Полезность вашего материала безгранична! Огромнейшее спасибо за справочные материалы, их оформление. Я еще не со всеми ознакомилась. Спасибо за помощь репетиторам по математике, школьным преподавателям и ученикам! Вы Учитель с большой буквы!
Спасибо за хороший материал, готовимся к олимпиаде по математике.
Александр Николаевич, большое спасибо за материал! У меня завтра экзамен, и ваш труд поможет сдать мне его на хорошую оценку. Так, как я поняла все по ваши справочникам, мне не объяснит ни один учитель — репетитор. Спасибо вам большое!
Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Окружность: вписанная в многоугольник или угол
Определения
Окружность (S) вписана в угол (alpha) , если (S) касается сторон угла (alpha) .
Окружность (S) вписана в многоугольник (P) , если (S) касается всех сторон (P) .
В этом случае многоугольник (P) называется описанным около окружности.
Теорема
Центр вписанной в угол окружности лежит на его биссектрисе.
Доказательство
Пусть (O) – центр некоторой окружности, вписанной в угол (BAC) . Пусть (B’) – точка касания окружности и (AB) , а (C’) – точка касания окружности и (AC) , тогда (OB’) и (OC’) – радиусы, проведённые в точки касания, следовательно, (OC’perp AC) , (OB’perp AB) , (OC’ = OB’) .
Значит, треугольники (AC’O) и (AB’O) – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда (angle CAO = angle BAO) , что и требовалось доказать.
Теорема
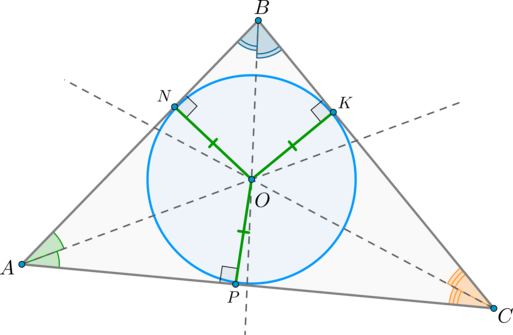
В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.
Доказательство
Проведем биссектрисы углов (angle A) и (angle B) . Пусть они пересеклись в точке (O) .
Т.к. (O) лежит на биссектрисе (angle A) , то расстояния от точки (O) до сторон угла равны: (ON=OP) .
Т.к. (O) также лежит на биссектрисе (angle B) , то (ON=OK) . Таким образом, (OP=OK) , следовательно, точка (O) равноудалена от сторон угла (angle C) , следовательно, лежит на его биссектрисе, т.е. (CO) – биссектриса (angle C) .
Таким образом, точки (N, K, P) равноудалены от точки (O) , то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.
Данная окружность единственна, т.к. если предположить, что существует другая вписанная в (triangle ABC) окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.
Таким образом, попутно была доказана следующая теорема:
Следствие
Биссектрисы треугольника пересекаются в одной точке.
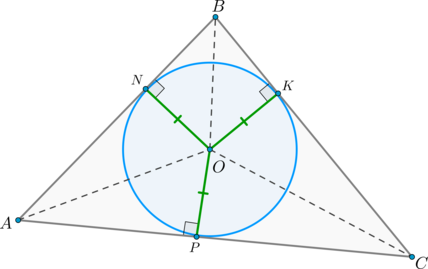
Теорема о площади описанного треугольника
Если (a,b,c) – стороны треугольника, а (r) – радиус вписанной в него окружности, то площадь треугольника [S_=pcdot r] где (p=dfrac2) – полупериметр треугольника.
Доказательство
Но (ON=OK=OP=r) – радиусы вписанной окружности, следовательно,
Следствие
Если в многоугольник вписана окружность и (r) – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на (r) : [S_<text>=pcdot r]
Теорема
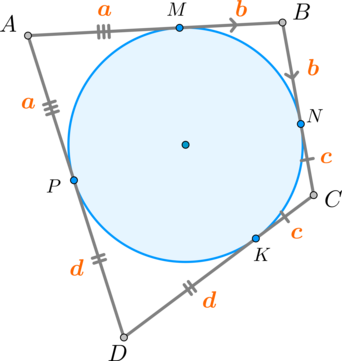
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство
Необходимость. Докажем, что если в (ABCD) вписана окружность, то (AB+CD=BC+AD) .
Пусть (M,N,K,P) – точки касания окружности и сторон четырехугольника. Тогда (AM, AP) – отрезки касательных к окружности, проведенные из одной точки, следовательно, (AM=AP=a) . Аналогично, (BM=BN=b, CN=CK=c, DK=DP=d) .
Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.
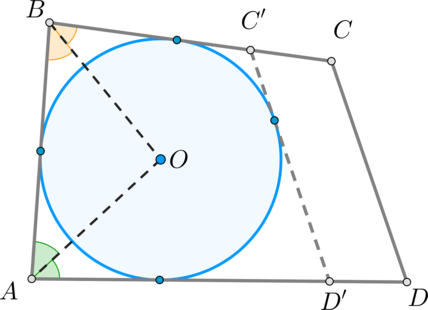
Проведем биссектрисы углов (angle A) и (angle B) , пусть они пересекутся в точке (O) . Тогда точка (O) равноудалена от сторон этих углов, то есть от (AB, BC, AD) . Впишем окружность в (angle A) и (angle B) с центром в точке (O) . Докажем, что эта окружность будет касаться и стороны (CD) .
Предположим, что это не так. Тогда (CD) либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).
Проведем касательную прямую (C’D’ parallel CD) (как показано на рисунке). Тогда (ABC’D’) – описанный четырехугольник, следовательно, (AB+C’D’=BC’+AD’) .
Т.к. (BC’=BC-CC’, AD’=AD-DD’) , то:
[AB+C’D’=BC-CC’+AD-DD’ Rightarrow C’D’+CC’+DD’=BC+AD-AB=CD]
Получили, что в четырехугольнике (C’CDD’) сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, (CD) касается окружности.
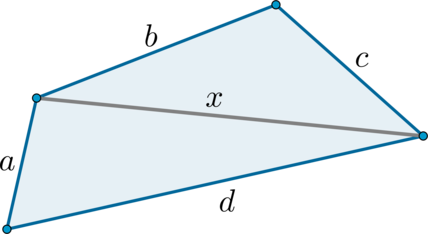
Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.
Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то (a+x>d) и (b+c>x) . Складывая данные неравенства, получим: (a+x+b+c>d+x Rightarrow a+b+c>d) . Следовательно, сумма любых трех сторон всегда больше четвертой стороны.
Теоремы
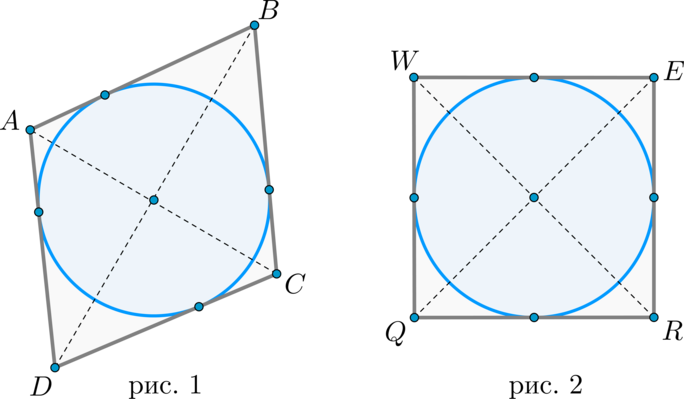
1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).
2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).
Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.
Доказательство
1) Рассмотрим параллелограмм (ABCD) , в который вписана окружность. Тогда (AB+CD=BC+AD) . Но в параллелограмме противоположные стороны равны, т.е. (AB=CD, BC=AD) . Следовательно, (2AB=2BC) , а значит, (AB=BC=CD=AD) , т.е. это ромб.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.
2) Рассмотрим прямоугольник (QWER) . Т.к. прямоугольник является параллелограммом, то согласно первому пункту (QW=WE=ER=RQ) , т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.
🔍 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать

Радиус описанной окружностиСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

ЕГЭ Задание 16 Окружности вписанные в уголСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Геометрия Точка O центр окружности вписанной в треугольник ABC BC = a AC = b угол AOB = 120 НайдитеСкачать

ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Вписанные углы в окружностиСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать