Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

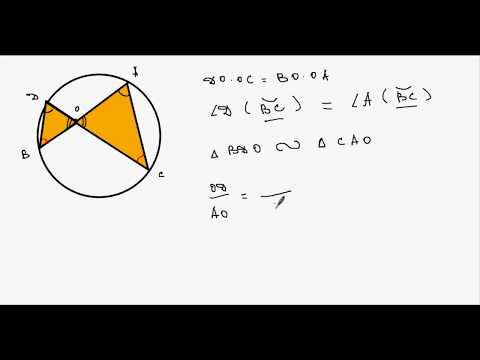
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Окружность

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Основные термины

Касательная

Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной

1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны.

Если две хорды окружности, AB и CD пересекаются в точке M , то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Свойства окружности

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку ( касательная ); иметь с ней две общие точки ( секущая ).
2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB .

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью

1. Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.

Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, равен 90°.

Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.

Длины и площади

1. Длина окружности C радиуса R вычисляется по формуле:

Площадь S круга радиуса R вычисляется по формуле:

Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется по формуле:

Площадь S сектора радиуса R с центральным углом в радиан вычисляется по формуле:

Вписанные и описанные окружности

Окружность и треугольник

• центр вписанной окружности — точка пересечения биссектристреугольника, ее радиус r вычисляется по формуле:

где S — площадь треугольника, а — полупериметр;

центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус R вычисляется по формуле:

здесь a, b, c — стороны треугольника, — угол, лежащий против стороны a , S — площадь треугольника;

центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы;

центр описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник — правильный.

Окружность и четырехугольники

• около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°:

в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон:

• около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
• около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
• в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.

Окружность. Свойства отрезков пересекающихся хорд, секущих и касательных

Презентация к уроку

Цель: повысить мотивацию к обучению; развивать вычислительные навыки, сообразительность, умение работать в команде.

Окружность — это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.

На слайде изображена окружность, отмечен ее центр — точка О, проведены два отрезка: ОА и СВ. Отрезок ОА соединяет центр окружности с точкой на окружности. Он называется РАДИУСОМ (по-латыни radius — “спица в колесе”). Отрезок СВ соединяет две точки окружности и проходит через ее центр. Это диаметр окружности (в переводе с греческого – “поперечник”).

Также нам понадобится определение хорды окружности — это отрезок, соединяющий две точки окружности (на рисунке – хорда DE).

Давайте выясним вопрос о взаимном расположении прямой и окружности.

Следующий вопрос и он будет основным: выяснить свойства, которыми обладают пересекающиеся хорды, секущие и касательные.

Доказывать эти свойства вы будете на уроках математики, а наша задача научиться применять эти свойства при решении задач, так как они находят широкое применение на экзаменах и в форме ЕГЭ, и в форме ГИА.

Задание для команд.

Изобразить и записать свойство пересекающихся в точке Р хорд КМ и NF.

Изобразить и записать свойство касательной КМ и секущей КF.

Изобразить и записать свойство секущих КМ и МF.

Далее продолжим работать в парах над решением простейших задач по применению этих свойств:

Используя данные на рисунке, найдите х. Слайд 5–6

Кто быстрее, правильней. С последующим обсуждением и проверкой решения всех задач. Отвечающие зарабатывают для своей команды поощрительные баллы.

Ну, а теперь приступим к решению более серьезных задач. Вашему вниманию предлагается три блока: пересекающиеся хорды, касательная и секущая, две секущие. Подробным образом разберем решение по одной задачи из каждого блока.

(Разбирается решение с подробной записью №4, №7, №12)

2. Практикум по решению задач

а) Пересекающиеся хорды

1. E – точка пересечения хорд AB и CD. AE=4, AB=10, СE:ED=1:6. Найти CD.

Решение:

2. E – точка пересечения хорд AB и CD. AB=17, CD=18, ED=2CE. Найти AE и BE.

Решение:

3. E – точка пересечения хорд AB и CD. AB=10, CD=11, BE=CE+1. Найти CE.

Решение:

4. E – точка пересечения хорд AB и CD. ED=2AE, CE=DE-1, BE=10. Найти CD.

Решение:

б) Касательная и секущая

5. Из одной точки проведены к окружности касательная и секущая. Касательная равна 6, секущая – 18. Определить внутренний отрезок секущей.

Решение:

6. Из одной точки проведены к окружности касательная и секущая. Найти касательную, если известно, что она меньше внутреннего отрезка секущей на 4 и больше внешнего отрезка на 4.

Решение:

7. Из одной точки проведены к окружности касательная и секущая. Найти секущую, если известно, что внутренний её отрезок относится к внешнему, как 3:1, а длина касательной равна 12.

Решение:

8. Из одной точки проведены к окружности касательная и секущая. Найти внешний отрезок, секущей, если известно, что внутренний её отрезок 12, а длина касательной 8.

Решение:

9. Касательная и секущая, исходящие из одной точки, соответственно равны 12 и 24. Определить радиус окружности, если секущая удалена от центра на 12.

Решение:

10. Из одной точки проведены к окружности две секущие, внутренние отрезки которых соответственно равны 8 и 16. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой. Найти длину каждой секущей.

Решение:

11. Из одной точки проведены к окружности две секущие. Внешний отрезок первой секущей относится к своему внутреннему, как 1:3. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой и относится к своему внутреннему отрезку, как 1:8. Найти длину каждой секущей.

Решение:

12. Через точку А, которая находится вне окружности на расстоянии 7 от её центра, проведен прямая, пересекающая окружность в точках В и С. Найдите длину радиуса окружности, если АВ=3, ВС=5.

Решение:

13. Из точки А проведены к окружности секущая длиной 12 см и касательная, составляющая внутреннего отрезка секущей. Найдите длину касательной.

Решение:

3. Закрепление знаний

Считаю, что вы обладаете достаточным запасом знаний, чтобы отправится в небольшое путешествие по лабиринтам вашего интеллекта, посетив следующие станции:

• Соображай-ка!
• Решай-ка!
• Отвечай-ка!

На станции можно находиться не более 6 минут. За каждое верное решение задачи команда получает поощрительные баллы.

Командам вручаются маршрутные листы:

Станция	Номера задач	Отметка о решении
Решай-ка!	№1, №3
Соображай-ка!	№5, №8
Отвечай-ка!	№10, №11

Станция	Номера задач	Отметка о решении
Соображай-ка!	№5, №8
Отвечай-ка!	№10, №11
Решай-ка!	№1, №3

Станция	Номера задач	Отметка о решении
Соображай-ка!	№5, №8
Отвечай-ка!	№10, №11
Решай-ка!	№1, №3

4. Подведение итогов

Хотелось бы подвести итоги нашего занятия:

Помимо новых знаний надеюсь, вы лучше познакомились друг с другом, приобрели опыт работы в команде. А как вы думаете, полученные знания находят где-то применение в жизни?

Поэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в своем романе “Каванг”, позволяют запечатлеть на всю жизнь некоторые теоремы и их применение. Читаем в романе следующую задачу:

“Лилия, на одну пядь поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в двух локтях от прежнего места; исходя из этого требовалось определить глубину озера” (1 пядь равна 10 дюймам, 2 локтя – 21 дюйму).

А решается эта задача на основе свойства пересекающихся хорд. Посмотрите на рисунок, и станет ясно, как находится глубина озера.

🌟 Видео