Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Биссектриса в равнобедренном треугольнике — свойства, теоремы и формулы
- Общие сведения
- Теоремы о биссектрисах
- Полезные свойства
- Пример решения
- Свойства биссектрисы равнобедренного треугольника
- Свойства биссектрисы равнобедренного треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Пример задачи
- 📸 Видео
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Свойство биссектрисы равнобедренного треугольникаСкачать

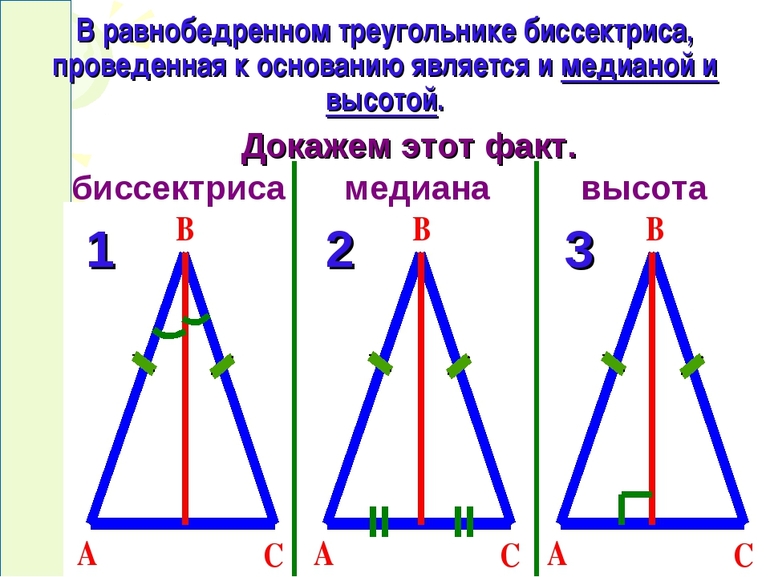
Биссектриса в равнобедренном треугольнике — свойства, теоремы и формулы
Видео:Равнобедренный треугольник. 7 класс.Скачать

Общие сведения
Геометрическая фигура является треугольником, если она состоит из трех точек, лежащих в одной плоскости и не лежащих на одной прямой. Она изучается в пятом классе. В геометрии принято сокращенное обозначение при помощи символа Δ, после которого следует писать произвольные три литеры (вершины) в алфавитном порядке. Например, ТUV.
Вершина — точка, из которой исходят два отрезка и образуют две стороны. Отрезок является элементом луча. Обозначается он двумя заглавными литерами (ТU, UV и т. д. ). Луч — часть прямой, имеющая только начало. Он необходим для построения отрезков, из которых состоят все фигуры геометрии.
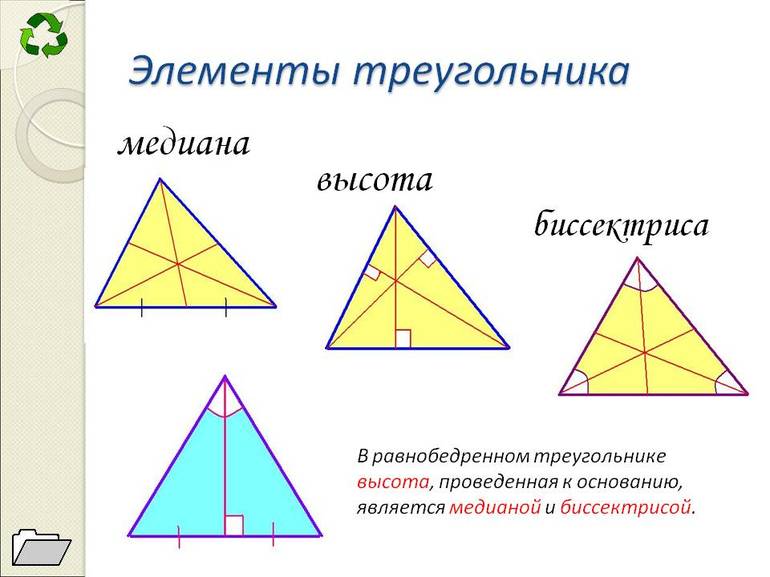
Прямая — линия, проходящая в бесконечном пространстве. У нее не существует начала и конца. Математики обозначают ее произвольной маленькой латинской буквой (например, m). Кроме того, у равнобедренного Δ существуют и дополнительные параметры — биссектриса, медиана и высота. Первая делит любой угол (сокращенное обозначение — ∠) при вершине, из которой она исходит, на два ∠ с эквивалентной градусной мерой, т. е. пополам.
Медиана соединяет вершину и середину противоположной стороны, а высота — простой перпендикуляр. Он начинается в вершине и находится внутри треугольника, опускаясь на противолежащую сторону.
Равнобедренный Δ — фигура, имеющая две равные боковые стороны. Следует отметить, что любая биссектриса равнобедренного треугольника является медианой. Это правило выполняется, когда она проведена к основанию фигуры. Существует еще один вид Δ. Он называется правильным или равносторонним. Для него справедливо такое утверждение, сформулированное учеными-математиками: любая высота является медианой и биссектрисой. Для решения задач по геометрии рекомендуется знать теорему о биссектрисе равнобедренного треугольника и ее свойства.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Теоремы о биссектрисах
Теорема о биссектрисах треугольника звучит таким образом: точка пересечения биссектрис — инцентр ΔTUV. Доказывается теорема по такому алгоритму:
- Из вершин T и U нужно провести биссектрисы TT’ и UU’ на противоположные стороны UV и TV соответственно.
- На чертеже видно, что они пересекаются в некоторой точке. Последнюю следует обозначить Z.
- Если предположить, что TT’ и UU’ не пересекаются, а параллельны (||), то секущей является сторона TU. В этом случае должно выполняться тождество: ∠(Т/2)+∠(U/2)=180.
- Однако утверждение в третьем пункте противоречит сумме градусных мер ∠ треугольника, поскольку ∠Т+∠U+∠V=180. Из выражения, полученного на третьем шаге алгоритма, следует, что ∠Т+∠U=360.
- На основании рассуждений можно сделать вывод, что Z — точка пересечения биссектрис.
- Таким же образом доказывается случай для вершины V и биссектрисы VV’.
- Точка Z — центр описанной окружности. Чтобы это доказать, нужно просто провести круг. На рисунке все вершины ΔTUV будут лежать на нем. Теорема полностью доказана.
Кроме того, существует еще одно утверждение, имеющее такой вид: любая высота равнобедренного треугольника является его биссектрисой и медианой.
Доказать его можно посредством такой методики:
- Начертить равнобедренный ΔTUV. У него стороны TU=UV, а TV — основание.
- Провести высоту UU’ на основание.
- Рассмотреть два прямоугольный Δ: TUU’ и UVU’. Они равны между собой, поскольку UU’ — общая, TU=UV и углы (∠Т=∠V) при основании — по определению равнобедренного Δ, а ∠ТU’U=∠UU’V — по построению.
- На основании третьего пункта можно сделать вывод о равенстве сторон TU’ и VU’, а также ∠U’UТ=∠VU’U. Следовательно, в первом случае UU’ — медиана, а во втором — биссектриса.
- На основании четвертого утверждения теорема доказана.
Кроме того, существуют определенные свойства, которые могут быть полезными при решении задач. Их получают из теорем и других тождеств, доказываемые математиками.
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Полезные свойства
Математики вывели пять полезных свойств для биссектрисы в равнобедренном Δ.
К ним относятся следующие:
- Свойство биссектрисы, проведенной к основанию равнобедренного треугольника: она есть медиана и высота.
- При проведении из вершин, образующих основание, углы, образованные ими, эквивалентны между собой.
- Если провести биссектрису TT’ из вершины при основании, то будет выполняться следующее тождество: TU/TV=UT’/T’V (отношение стороны к основанию эквивалентно частному из двух отрезков, полученных при построении).
- Длина биссектрисы, проведенной к основанию, эквивалентна корню второй степени из квадрата боковой стороны без четвертой части квадрата основания: UU’=[m 2 — (¼)*n 2 ](^½), где m и n — длина боковой стороны и основания.
- Через точку пересечения проходит круг, касающийся вершин основания.
Следует отметить, что в равностороннем треугольнике каждая биссектриса будет отсекать равные углы из каждой вершины.
В нем можно провести их всего три, а в равнобедренном — 2 высоты, 2 медианы, 2 биссектрисы, а также одну к основанию.
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Пример решения
Чтобы усвоить материал, необходимо решить задачу по геометрии. Ее условие имеет такой вид:
- Периметр равнобедренного Δ равен 40 см.
- Основание больше боковой стороны на 10 см.
Необходимо найти значение высоты. Решать нужно по такому алгоритму:
- Составить уравнение: 40=2*t+(t+10), где t — боковая сторона, а (t+10) — основание.
- Раскрыть скобки: 40=2*t+t+10.
- Привести подобные коэффициенты:3t=30.
- Найти неизвестную: t=10 (см).
- Вычислить основание: 10+10=20 (см).
- Определить высоту: h= [100+((¼)*20)^2]^(½)=5[5]^(½) (см).
Следовательно, высота равнобедренного Δ со сторонами 10 и 20 см эквивалентна 5[5]^(½) см. Существуют и более сложные задачи, в которых требуется составлять уравнения. Например, условие одной из них имеет такой вид:
- Высота, опущенная из вершины на основание (ТТ’), равна 20 см.
- Основание больше стороны на 5 см.
Необходимо найти периметр треугольника. Для решения задачи необходимо составить определенный алгоритм:
- Обозначить стороны: основание — n, сторона — m и высота — h.
- Периметр P: Р=2m+n.
- Записать формулу, руководствуясь первым и четвертым свойствами биссектрисы: h=[m 2 -(¼)*n 2 ]^(½).
- Записать связь сторон, обозначив боковую сторону переменной t: t=t+5.
- Подставить в соотношение во втором пункте: 20=[t 2 -(¼)*(t+5)^2]^(½).
- Возвести обе части в квадрат: 400=t 2 -(¼)*(t+5)^2.
- Раскрыть скобки: 400=t 2 -(¼)*(t 2 +10+25)=t 2 -(¼)t 2 −10/4−25/4=(¾)t 2 -(10/4)-25/4=(¼)*(3t 2 -10−25).
- Решить квадратное уравнение, сократив на ¼ обе части: (3t 2 -10t-25)=200.
- Первый корень равен -7, а второй — +25. Второе значение подходит, поскольку является положительным числом.
- Основание вычисляется таким образом: n=25+5=30 (см).
- Если подставить полученное значение для проверки в соотношение h=[t 2 -(¼)*(t+5)^2]^(½), то получится такое выражение: 20=[25 2 -(¼)*30 2 ]^(½)=[625−900/4]^(½)=[625−225]^(½)=20. Значение найдено верно.
- Периметр находится по формуле: P=25*2+30=80 (см).
Задача решена в полном объеме. Из методики решения видно, что сначала нужно записать основную формулу, а затем найти неизвестные в ней величины по другим вспомогательным тождествам.
Таким образом, при решении задач по геометрии необходимо знать основные определения, формулы, свойства и теоремы, которые также могут быть полезны.
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

Свойства биссектрисы равнобедренного треугольника
В данной публикации мы рассмотрим основные свойства биссектрисы равнобедренного треугольника (внутренней и внешней), а также разберем пример решения задачи по данной теме.
Примечание: напомним, что равнобедренным называется треугольник, в котором две стороны равны (боковые), а третья является основание фигуры.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства биссектрисы равнобедренного треугольника
Свойство 1
В равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.
- AB = BC, т.к. являются боковыми сторонами равнобедренного △ABC;
- AF = CG, т.к. это биссектрисы, проведенные к боковым сторонам треугольника (или биссектрисы углов BAC и ACB, которые также равны между собой).
Обратная формулировка: если две из трех биссектрис в треугольнике равны, значит он является равнобедренным.
Свойство 2
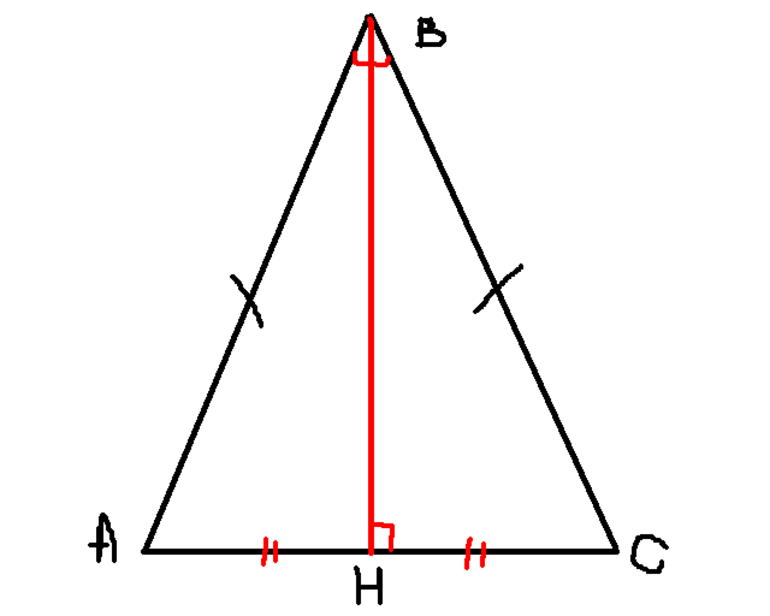
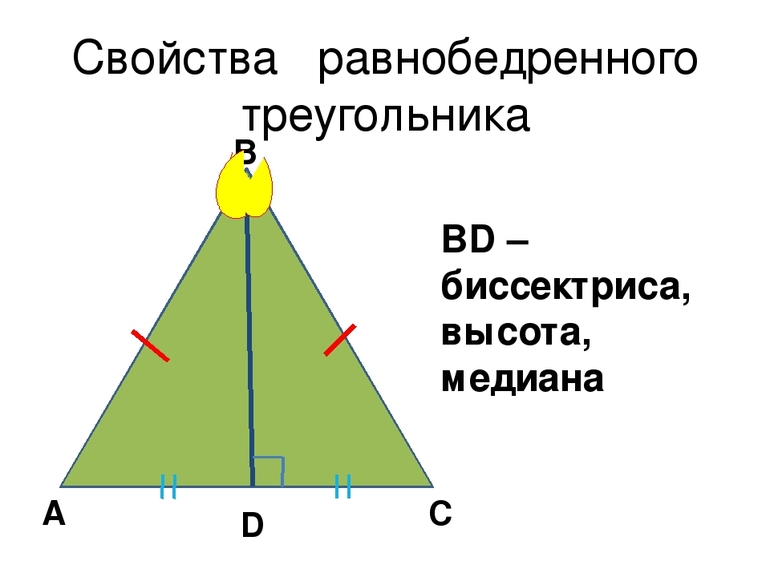
В равнобедренном треугольнике биссектриса, проведенная к основанию, одновременно является и медианой и высотой.
- BH – биссектриса угла ABC, проведенная к основанию AC;
- BH – медиана, значит она делит AC пополам, т.е. AH = HC;
- BH – высота, следовательно, она перпендикулярна AC.
Свойство 3
Если известны стороны равнобедренного треугольника, то длину биссектрисы, проведенную к основанию, можно посчитать по формуле:
Примечание: данная формула следует из теоремы Пифагора ( l и a – катеты прямоугольного треугольника, b – его гипотенуза).
Свойство 4
Внешняя биссектриса угла равнобедренного треугольника, расположенного напротив его основания, параллельна этому основанию.
- BD – внешняя биссектриса ∠ABC треугольника;
- BD параллельна основанию AC.
Примечание: к равнобедренному треугольнику применимы и другие свойства биссектрисы, приведенные в нашей публикации – “Определение и свойства биссектрисы угла треугольника”.
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Пример задачи
Биссектриса равнобедренного треугольника с боковой стороной 25 см равняется 20 см. Найдите периметр фигуры.
Решение
Воспользуемся формулой, приведенной в Свойстве 3, чтобы найти длину основания.
a 2 = b 2 – l 2 = 25 2 – 20 2 = 225 .
Извлекаем квадратный корень из найденного значения и получаем 15 см.
Следовательно, основание треугольника равно 30 см (15 см ⋅ 2).
Периметр фигуры равен сумме всех ее сторон, т.е.: 25 см + 25 см + 30 см = 80 см.
📸 Видео
Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Свойство биссектрисы треугольникаСкачать

Свойства биссектрисы треугольникаСкачать

Свойства биссектрисыСкачать

Геометрия 7 класс (Урок№32 - Повторение. Равнобедренный треугольник и его свойства.)Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Решение задач на свойства биссектрисы и углов при основании равнобедренного треугольника.Урок 8. 7клСкачать

✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать