- Определение
- Теорема
- Доказательство теоремы
- Треугольник — определение и основные свойства и виды треугольника
- Определение треугольника
- Высота треугольника
- Виды треугольника
- Виды треугольников по углам
- Виды треугольников по сторонам
- Свойства сторон треугольника
- Правило существования треугольника
- Свойство углов в треугольнике
- Элементы композиции
- Урок по теме «Треугольник, существование треугольника, равного данному»
- 📺 Видео
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.
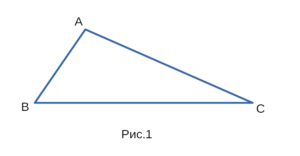
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
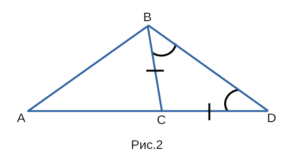
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы
- Проведем отрезок CD равный отрезку CB.
- △BCD — равнобедренный, значит ∠ CBD=∠CDB.
- Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Треугольник — определение и основные свойства и виды треугольника
Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Определение треугольника
Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.
Посмотрите на треугольник на рисунке.
У него три вершины — 






будут звать 
По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.
В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Высота треугольника
В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.
Например, в треугольнике 

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.
В этом треугольнике три высоты 


Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Виды треугольника
Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.
Виды треугольников по углам
В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный
, треугольник бывает остроугольным, тупоугольным или прямоугольным.
Посмотрите на рисунки — перед вами три основных вида треугольника:
Виды треугольников по сторонам
Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.
На рисунке показаны равносторонний и равнобедренный треугольники.
Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Свойства сторон треугольника
Треугольник имеет важные свойства и характеристики.
Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.
Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.
Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:
Например, пусть наш треугольник имеет длины двух сторон 

Решение: согласно свойству сторон треугольника, получим:
Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.
Правило существования треугольника
Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.
Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.
Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?
Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.
Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Свойство углов в треугольнике
Сумма всех углов в треугольнике равна 
Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна 
Например, пусть известно, что в треугольнике 



Так как сумма углов в треугольнике равна 

Ответ: 
Видео:Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

Элементы композиции
Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.
А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:
Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.
Видео:Треугольники. 7 класс.Скачать

Урок по теме «Треугольник, существование треугольника, равного данному»
Разделы: Математика
Обучающая: обобщить ЗУНы по изученной теме.
Развивающая: развивать умения применять теоретический материал при решении задач; развивать логическое мышление. Учить мыслить, рассуждать, анализировать, обобщать.
Воспитывающая: формировать навык анализа и оценки собственной деятельности (самооценка).
Задачи:
- Обобщить изученный материал, задать мотивацию. Учить воспитанников логично строить новую для них науку ГЕОМЕТРИЮ. Проанализировать структуру формулировки определения и свойств фигур (отрезков и углов по аналогии; полупрямой и полуплоскости).
- Повести устный опрос учащихся с самооценкой.
- Провести самостоятельную работу «Решение задач по готовым чертежам» (самооценка).
- Провести рефлексию полученных результатов.
- Задать согласно результатам урока домашнее задание.
Оборудование:
1. Организующий момент, мотивация на урок, постановка целей и задач (слайд1).
Сообщается план урока.
— Итак, ребята, мы продолжаем строить новую науку — ГЕОМЕТРИЮ. Сейчас мы повторим и обобщим те знания, которые вы уже имеете, проведём аналогии, где это возможно, и будем продолжать знакомиться с новыми понятиями. А также Вы сами проверите, как полученные знания Вы применяете при решении задач. Узнаете много нового и интересного о геометрии. На каждом этапе урока вы оцените себя. Результаты занесёте в таблицу:
| Этап урока | Название этапа | Самооценка по 5-бальной шкале |
| 1 | Знание теории | |
| 2 | Самостоятельная работа | |
| 3 | Изучение нового материала | |
| 4. | Практическое применение |
2. Повторение (слайды 2 -16).
Воспитанники выставляют себе оценку в карточку за знание теории (самооценка).
3. Самостоятельная работа (слайды 17-18).
У каждого воспитанника на столе лист с готовыми чертежами для 10 задач. Необходимо кратко записать решение задач по теме «Углы» (применение свойств). См. приложение 1. Каждый может выбрать себе для решения 5 любых задач или больше (в зависимости от способностей и подготовки). На решение отводится 8-10 минут. Затем самопроверка. На доске — слайд с ответами. Самооценка (выставление в лист самоконтроля).
-Внимательно посмотрите на картинку под звуки музыки Шнитке (30-40сек). Из каких фигур она составлена? Да, большинство фигур — треугольники.
Изучение нового материала.
Воспитанники, зная заранее тему урока, выссказывают свои пожелания, о чём бы они хотели узнать сегодня на уроке.
Обсуждение эпиграфа, постановка целей данного этапа урока (слайд20).
Высшее проявление духа — это разум.
Высшее проявление разума — это геометрия.
Клетка геометрии — треугольник.
Он так же неисчерпаем, как и вселенная.
И.Ф. Шарыгин
Воспитанники показывают треугольники в окружающей жизни. Пытаются сформулировать определение треугольника. Поиск и научная формулировка определения треугольника. Показываются и обозначаются стороны и углы треугольника. Подчёркивается разница в обозначении углов и треугольников. Треугольник — это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
В любом треугольнике:
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
Задача: воспитанники решили у себя в чайной поставить стол треугольной формы с одной ножкой. Где должно быть основание ножки? В руках фанерный треугольник, и методом проб находится самая устойчивая точка приложения ножки. А если не » на глаз», а научно? Как называется и как находится эта точка? Формулируются определения медианы и центроида.
Рассматриваются виды треугольников (по углам) и существование треугольника, равного данному.
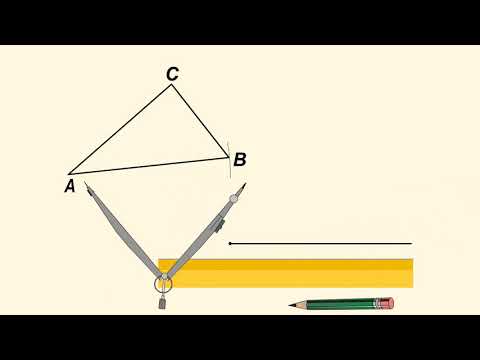
На рисунке изображен треугольник ABC и луч «a».? Переместим треугольник ABC так, чтобы его вершина A совместилась с началом луча «a», вершина B попала на луч «a», а вершина C оказалась в заданной полуплоскости относительно луча «a» и его продолжения. Вершины нашего треугольника в этом новом положении обозначим A1, B1, C1. Треугольник A1B1C1 равен треугольнику ABC. Существование треугольника A1B1C1, равного треугольнику ABC и расположенного указанным образом относительно заданного луча a, мы относим к числу основных свойств простейших фигур.
Сформулируем это свойство так:
Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой. Существование треугольника, равного данному.
Два треугольника называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие стороны должны лежать против соответствующих углов.
Существование треугольника, равного данному, мы относим к числу аксиом. (Казалось бы, что это очевидно, но ведь доказать нельзя!)
Вспомните определение периметра. Решим задачу.
Необходимо огородить участок земли треугольной формы. Известно, что имеется 47 метров изгороди. Одна сторона треугольника на 7 метров меньше другой и в 2 раза меньше третьей. Найти стороны треугольника (участка).
Обсуждение и решение задачи (чертёж, дано, найти, решение). Слайды 21-26.
Самооценка данного этапа в листе самоконтроля.
5. Домашнее задание (слайд27).
1. Пункты 9 и 10 изучить. Повторить теорию п.1-8.
3. Дополнительно (распечатка): а) Сколько треугольников изображено на рисунке?
б) На сколько частей разбивают плоскость правильные звездчатые многоугольники, изображенные на рисунке?
6. Это интересно.
1. Воспитанникам показываются две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жесткой: сдвигая или раздвигая концы, мы можем менять угол между ними. Теперь возьмем еще одну рейку и скрепим ее концы со со свободными концами первых двух реек. Полученная конструкция будет уже жесткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Свойство жесткости треугольника широко используют в практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку. Такой же принцип используются при установке кронштейна. (слайды 28-30).
2. 19 марта 2012 года Шуховской башне на Шаболовке исполнится 90 лет. Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций. Высоковольтные линии электропередачи. Треугольники делают конструкции надежными. Треугольники в конструкции мостов (слайды 31-33).
3. С древних времен известен очень простой способ построения прямых углов на местности. Этот способ применялся тысячелетия назад строителями египетских пирамид. Три воспитанника выходят и натягиваю египетский треугольник со сторонами 3, 4, 5 с помощью верёвки с узелками, завязанными на равных расстояниях друг от друга (слайды 34 — 35).
4. Слайды 36-43 . Показываются различные применения треугольника в архитектуре, дизайне, при определении местонахождения эпицентра землетрясения и др.
7. Рефлексия. Итоги урока.
Организация рефлексии и обратной связи, коррекция промежуточных результатов. Создание условий для развития умений анализировать результат своей деятельности и ставить перед собой посильные задачи.
1. Какова структура определения нового понятия?
2. Что необходимо запомнить, а что можно сформулировать по аналогии?
3. Считаете ли вы, что цель урока достигнута?
4. Что нового узнали на уроке?
5. Что хотелось бы повторить на следующих уроках?
6. Как оцениваете свою работу на уроке? (сдают листы самоконтроля, самооценки).
Составление «картины» деятельности на уроке: «Мы узнали:», «Мы учились:», «Мы смогли:», «У нас не получилось:», анализ её успешности: «Смогли, потому что:», «Не получилось, потому что:», «Дома и на следующем уроке надо потренироваться в:»
📺 Видео
По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Внешний угол треугольникаСкачать

Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Построение угла, равного данному. 7 класс.Скачать

Параллельные прямые | Математика | TutorOnlineСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Виды треугольниковСкачать

Отношение площадей треугольников с равным угломСкачать
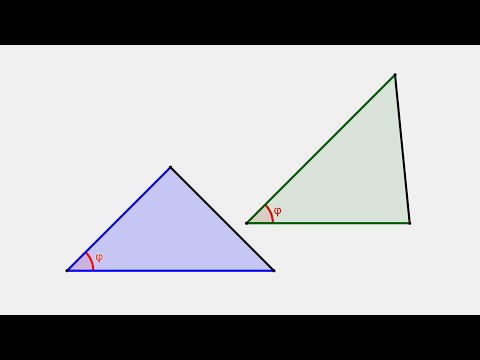
Построение треугольника, равного данномуСкачать