Сумма противоположных углов трапеции вписанной в окружность равна 180

ВПИСАННЫЕ И ОПИСАННЫЕ МНОГОУГОЛЬНИКИ,

§ 106. СВОЙСТВА ВПИСАННЫХ И ОПИСАННЫХ ЧЕТЫРЁХУГОЛЬНИКОВ.

Теорема 1. Сумма противоположных углов вписанного четырёхугольника равна 180°.

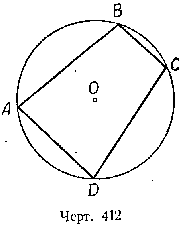
Пусть в окружность с центром О вписан четырёхугольник ABCD (черт. 412). Требуется доказать, что / А + / С = 180° и / В + / D = 180°.

/ А, как вписанный в окружность О, измеряется 1 /₂ BCD.
/ С, как вписанный в ту же окружность, измеряется 1 /₂ BAD.

Следовательно, сумма углов А и С измеряется полусуммой дуг BCD и BAD в сумме же эти дуги составляют окружность, т. е. имеют 360°.
Отсюда / А + / С = 360° : 2 = 180°.

Аналогично доказывается, что и / В + / D = 180°. Однако это можно вывести и иным путём. Мы знаем, что сумма внутренних углов выпуклого четырёхугольника равна 360°. Сумма углов А и С равна 180°, значит, на сумму других двух углов четырёхугольника остаётся тоже 180° .

Теорема 2 (обратная). Если в четырёхугольнике сумма двух противоположных углов равна 180°, то около такого четырёхугольника можно описать окружность.

Пусть сумма противоположных углов четырёхугольника ABCD равна 180°, а именно
/ А + / С = 180° и / В + / D = 180° (черт. 412).

Докажем, что около такого четырёхугольника можно описать окружность.

Доказательство. Через любые 3 вершины этого четырёхугольника можно провести окружность, например через точки А, В и С. Где будет находиться точка D?

Точка D может занять только одно из следующих трёх положений: оказаться внутри круга, оказаться вне круга, оказаться на окружности круга.

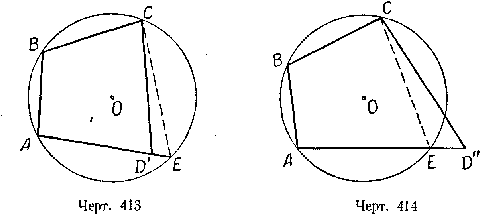
Допустим, что вершина окажется внутри круга и займёт положение D’ (черт. 413). Тогда в четырёхугольнике ABCD’ будем иметь:

Продолжив сторону AD’ до пересечения с окружностью в точке Е и соединив точки Е и С, получим вписанный четырёхугольник АВСЕ, в котором по прямой теореме

Из этих двух равенств следует:

но этого быть не может, так как / D’, как внешний относительно треугольника CD’E, должен быть больше угла Е. Поэтому точка D не может оказаться внутри круга.

Так же доказывается, что вершина D не может занять положение D» вне круга (черт. 414).

Остаётся признать, что вершина D должна лежать на окружности круга, т. е. совпасть с точкой Е, значит, около четырёхугольника ABCD можно описать окружность.

Следствия. 1. Вокруг всякого прямоугольника можно описать окружность.

2. Вокруг равнобедренной трапеции можно описать окружность.

В обоих случаях сумма противоположных углов равна 180°.

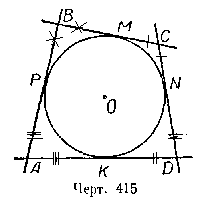
Теорема 3. В описанном четырёхугольнике суммы противоположных сторон равны. Пусть четырёхугольник ABCD описан около окружности (черт. 415), т. е. стороны его АВ, ВС, CD и DA — касательные к этой окружности.

Требуется доказать, что АВ + CD =AD + ВС. Обозначим точки касания буквами М, N, К, Р, На основании свойств касательных, проведённых к окружности из одной точки (§ 75), имеем:

АР = АК;
ВР = ВМ;
DN = DK;
CN = СМ.

Сложим почленно эти равенства. Получим:

АР + ВР + DN + CN = АК + ВМ +DK + СМ,

т. е. АВ + CD = AD + ВС, что и требовалось доказать.

1. Во вписанном четырёхугольнике два противоположных угла относятся как 3 : 5,
а другие два относятся как 4 : 5. Определить величину этих углов.

2. В описанном четырёхугольнике сумма двух противоположных сторон равна 45 см. Остальные две стороны относятся как 0,2 : 0,3. Найти длину этих сторон.

Видео:Геометрия Если в четырехугольнике сумма противолежащих углов равна 180, то около него можно описатьСкачать

Трапеция.

Трапеция — четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются её основаниями, а две другие — боковыми сторонами.

Трапеция называется равнобедренной, если её боковые стороны равны.

Трапеция называется прямоугольной, если у нее два угла прямые.

Основные свойства трапеции:

1. Сумма углов при каждой боковой стороне трапеции равна 180°.
2. Средняя линия трапеция параллельна её основаниям и равна их полусумме.
3. В любой трапеции следующие точки лежат на одной прямой: точка пересечения продолжений боковых сторон, середины оснований и точка пересечения диагоналей.
4. Треугольники, образованные отрезками диагоналей и основаниями трапеции, подобны.
5. Треугольники, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Если сумма углов, при любом основании трапеции, равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
8. Биссектриса любого угла трапеции отсекает от нее равнобедренный треугольник.
9. Биссектрисы углов, при боковой стороне трапеции, перпендикулярны.
10. Если в трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
11. Отрезок, заключенный между боковых сторон трапеции, параллельный основаниям трапеции и проходящий через точку пересечения ее диагоналей — среднее гармоническое оснований трапеции.

Свойства равнобедренной трапеции:

1. Диагонали равны.
2. Углы при основании равны.
3. Сумма противоположных углов равна 180°.
4. Около равнобедренной трапеции можно описать окружность.
5. Высота, опущенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, больший из которых равен полусумме оснований, а меньший — полуразности оснований.

Описанная трапеция:

1. Если вокруг трапеции можно описать окружность, то трапеция равнобедренная.
2. Радиус вписанной окружности равен среднему геометрическому длин отрезков, на которые радиус вписанной окружности делит боковую сторону, точкой касания.
3. Радиус вписанной окружности равен половине высоты трапеции.

Вписанная трапеция:

1. Трапецию можно вписать в окружность,если сумма длин оснований равна сумме длин боковых сторон.

Площадь трапеции:

1. Формула площади трапеции через основания и высоту: S=0,5·(a+b)·h.
2. Формула площади трапеции через диагонали и угол между ними: S=0,5·d₁·d₂·sinφ.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Геометрия 11-3. Трапеции, вписанные в окружность и описанные около окружности. Задача 3Скачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Радиус описанной окружности трапецииСкачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

🎬 Видео

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Вписанный в окружность четырёхугольник.Скачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Если в четырёхугольник можно вписать окружностьСкачать

Окружность, вписанная в трапециюСкачать

16 задача ОГЭ: четырёхугольник, вписанный в окружность; подобные треугольникиСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

ВПИСАННЫЙ ЧЕТЫРЕХУГОЛЬНИК. Готовимся к ЕГЭ. ЧАСТЬ I #shorts #математика #егэ #огэ #геометрияСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Вписанный четырехугольник, сумма противоположных угловСкачать

Задача про трапецию, описанную около окружностиСкачать

Бицентрический четырёхугольник. Вписанно-описанная трапецияСкачать

Вписанная и описанная трапеции. КлассикаСкачать