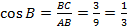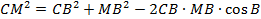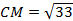Сумма косинусов в треугольнике

Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Формулы суммы и разности синусов и косинусов

Запишем, как выглядят формулы суммы и разности для синусов и для косинусов

Формулы суммы и разности для синусов

sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2

cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2

Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.

Определения формул сумм и разности синусов и косинусов

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.

Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.

Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Вывод формул суммы и разности синусов и косинусов

Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже

sin ( α + β ) = sin α · cos β + cos α · sin β sin ( α — β ) = sin α · cos β — cos α · sin β cos ( α + β ) = cos α · cos β — sin α · sin β cos ( α — β ) = cos α · cos β + sin α · sin β

Также представим сами углы в виде суммы полусумм и полуразностей.

α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2

Переходим непосредственно к выводу формул суммы и разности для sin и cos.

Вывод формулы суммы синусов

В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим

sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2

Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)

sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу

sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2

Действия по выводу остальных формул аналогичны.

Вывод формулы разности синусов

sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2

Вывод формулы суммы косинусов

Вывод формулы разности косинусов

cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Примеры решения практических задач

Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.

Пример 1. Проверка формулы суммы синусов двух углов

α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2

Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.

Пример 2. Применение формулы разности синусов

α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2

С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.

Видео:Сумма и разность синусов. Тригонометрия-13Скачать

Теорема косинусов и синусов

О чем эта статья:

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Формулировка и доказательство теоремы косинусов

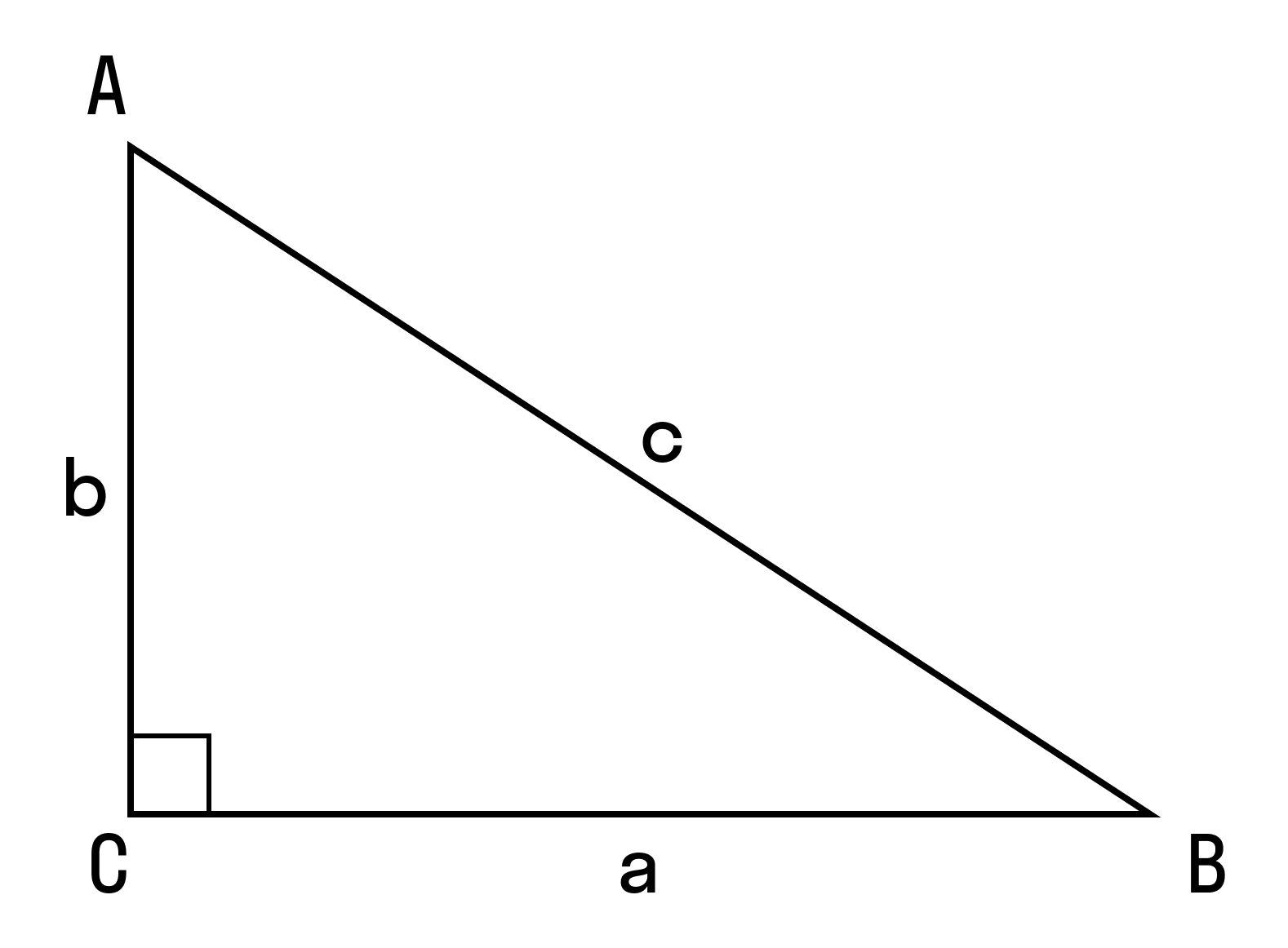
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

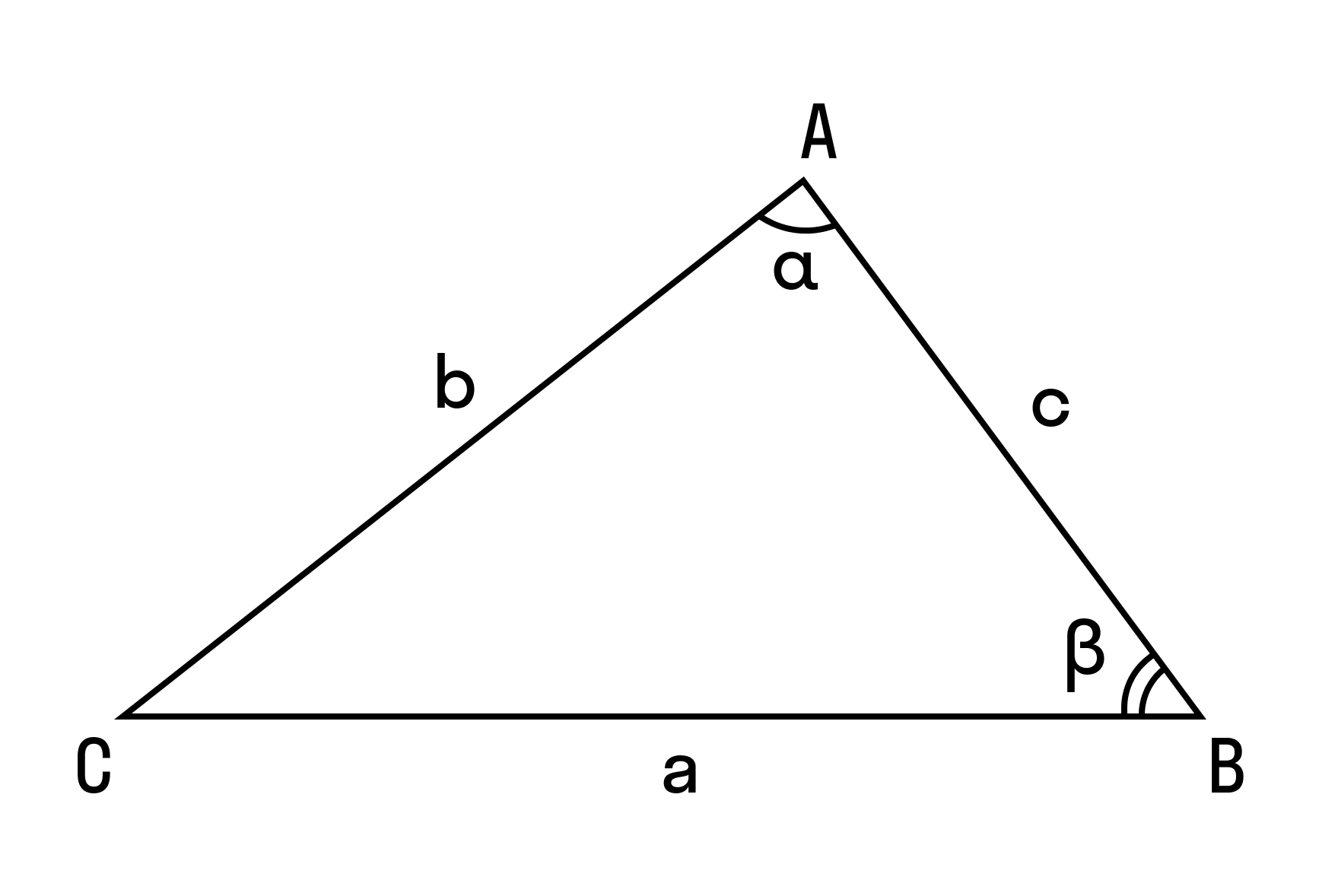
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

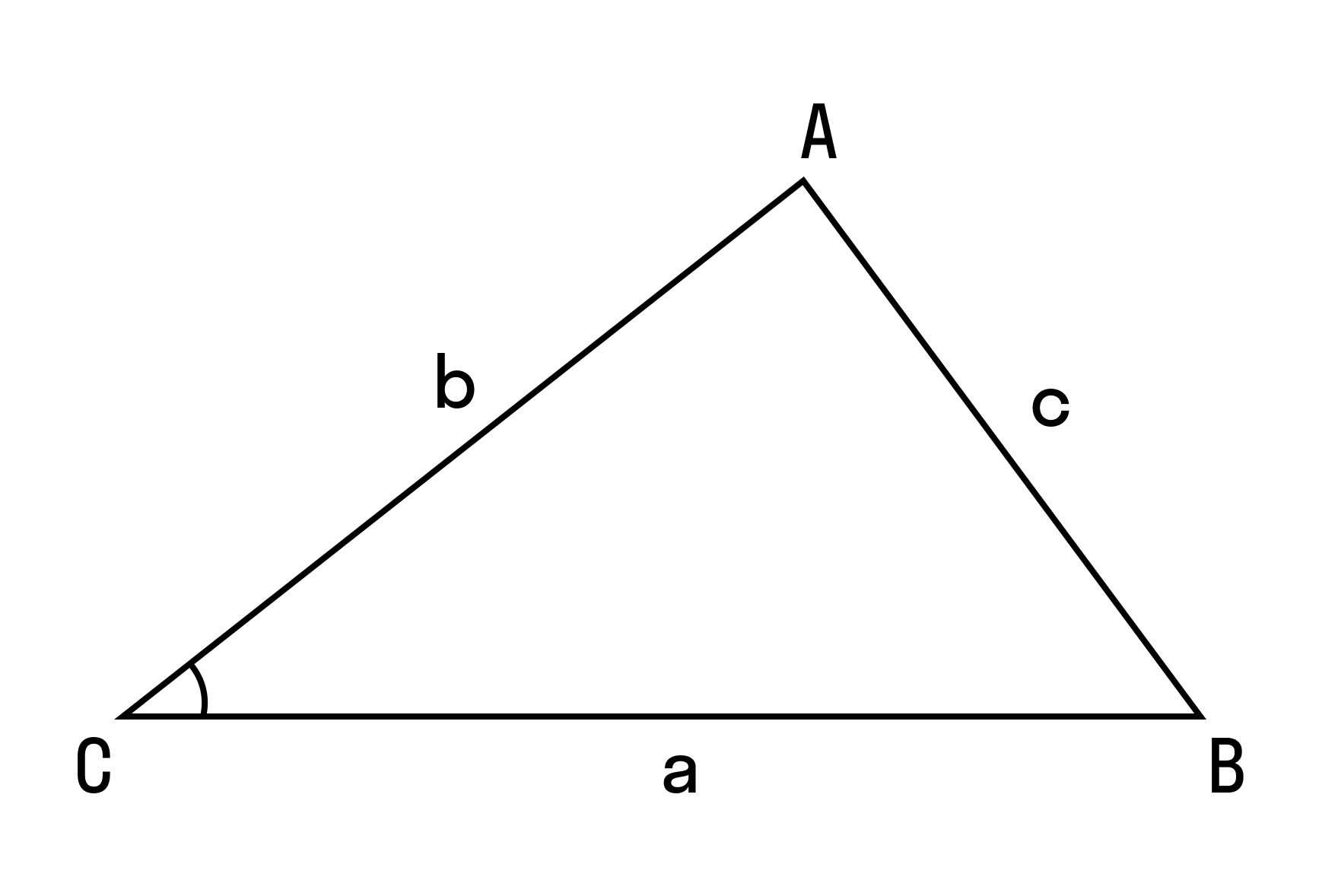
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

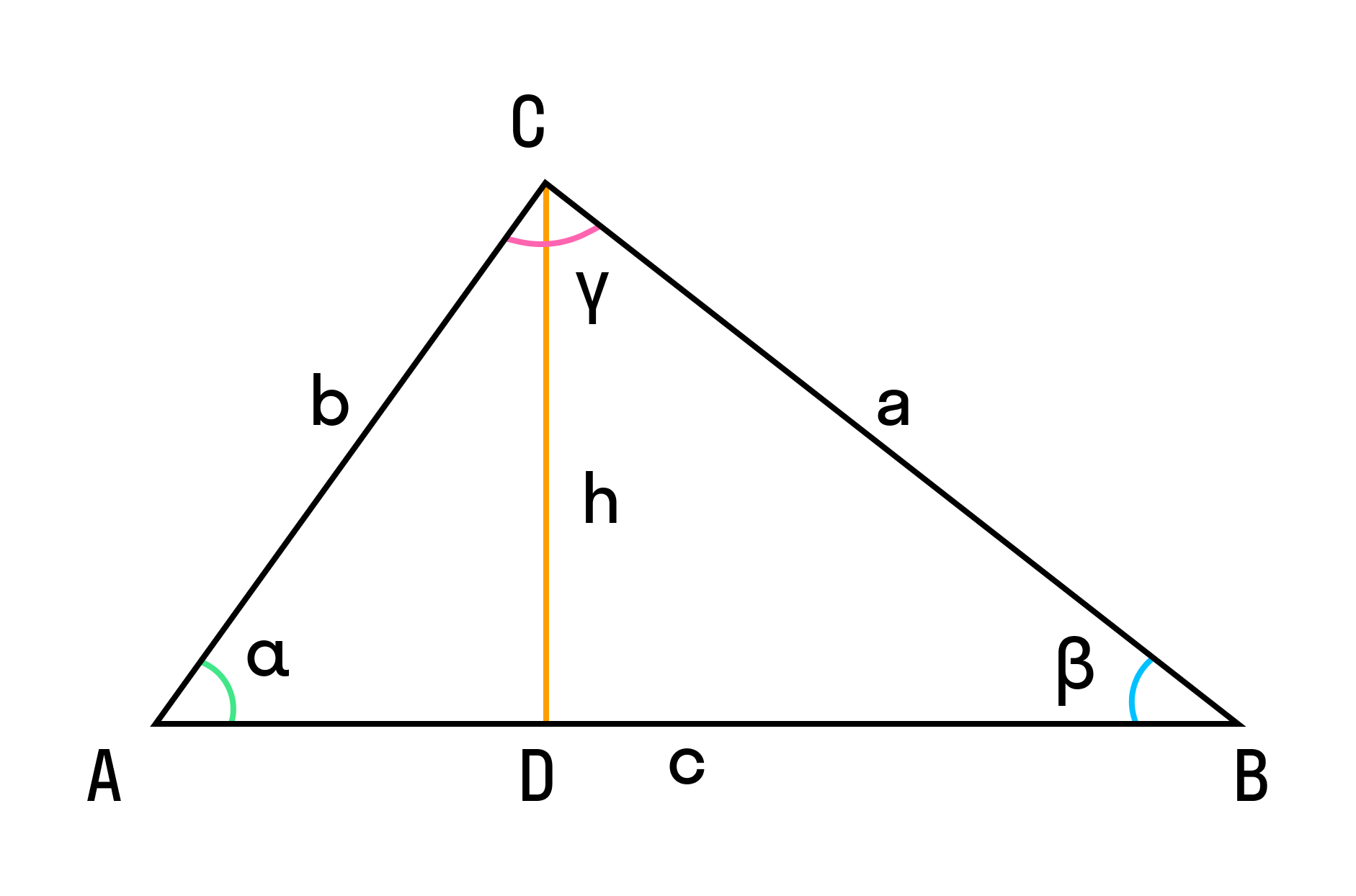
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Видео:9 класс, 14 урок, Теорема косинусовСкачать

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Видео:№1025. С помощью теорем синусов и косинусов решите треугольник ABC, если:Скачать

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

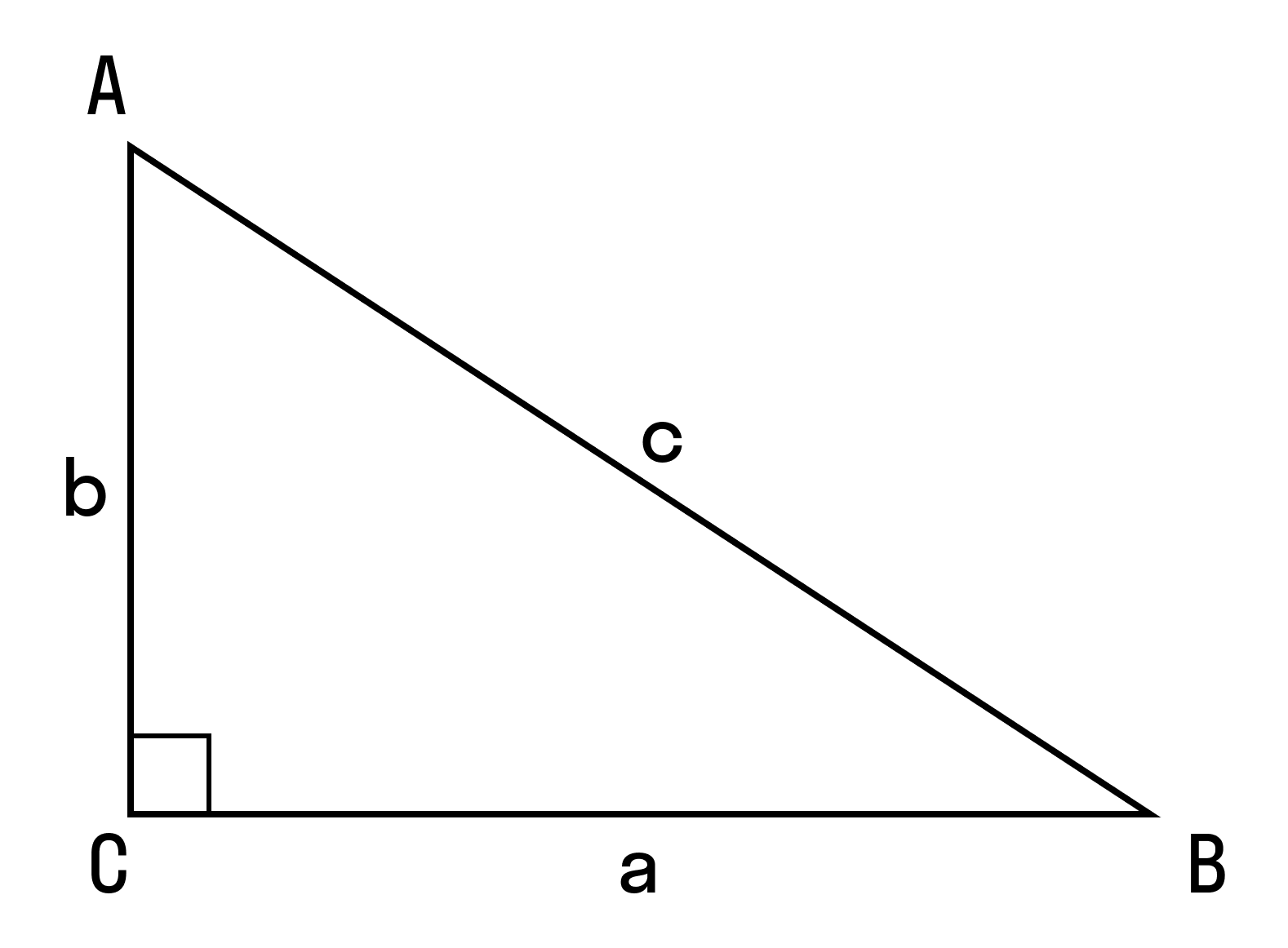
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

• Если c 2 2 + b 2 , то ∠C — острый.

Видео:Теорема косинусов #shortsСкачать

Теорема косинусов. Доказательство теоремы косинусов.

Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.

Теорема косинусов:

Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Видео:Теорема косинусов для треугольникаСкачать

Следствие из теоремы косинусов.

• Теорема косинусов используется для определения cos угла треугольника:

h 2 = a 2 — (c – b cos α) 2 (2)

Приравниваем правые части уравнений (1) и (2):

b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2

a 2 = b 2 + c 2 — 2bc cos α.

Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определить стороны b и c:

🎬 Видео

Формулы суммы и разности косинуса и синуса Алгебра 10 классСкачать

ТЕОРЕМА КОСИНУСОВ. Задачи на произвольные треугольникиСкачать

9 класс, 13 урок, Теорема синусовСкачать

Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

вывод формул синус и косинус суммы угловСкачать

ТЕОРЕМА КОСИНУСОВ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Синусы и косинусы. Кому они нужны?Скачать

Сумма косинусов треугольника меньше или равно 3/2Скачать