Вопрос по геометрии:
Найти радиус круга, описанного около равностороннего треугольника со стороной а=12 корень из 3
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Есть формула a=R√3. а=12√3., то R= a/√3=12√3/√3=12
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать
Сторона равностороннего треугольника 12 3 найти радиус окружности
Задание 9. Медиана равностороннего треугольника равна 12√3. Найдите его сторону.
В равностороннем треугольнике все стороны равны, а медиана является также и высотой h (см. рисунок).
Из рисунка видно, что сторону 
равностороннего треугольника можно найти из прямоугольного треугольника, в котором один катет является высотой h, второй – половина основания, равная a/2, к которому проведена высота, а роль гипотенузы будет играть сторона треугольника, равная a. Таким образом, по теореме Пифагора, можно записать равенство:
,
откуда выразим сторону треугольника:
Подставим вместо h=12√3, получим квадрат стороны треугольника:
и сторона равна
.
Задание 10. В треугольнике ABC известно, что АС = 40 , ВС = 30 , угол С равен 90°. Найдите радиус описанной около этого треугольника окружности.
Радиус описанной окружности вокруг прямоугольного треугольника лежит на середине его гипотенузы. Найдем длину гипотенузы прямоугольного треугольника по теореме Пифагора, имеем:
,
и радиус описанной окружности, равен:
.
Видео:ОГЭ 2020 задание 17Скачать
Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Видео:ОГЭ 16🔴Скачать
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
🎦 Видео
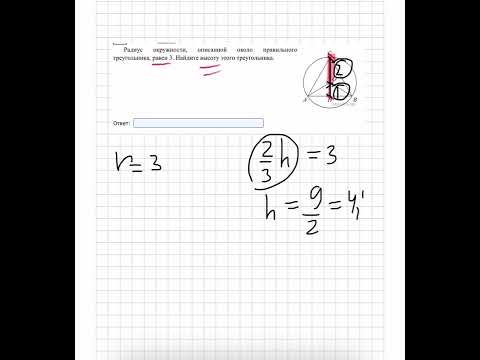
Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать
Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать
№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать
Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать
Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать
Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать
Задача 6 №27892 ЕГЭ по математике. Урок 126Скачать
15 задание треугольники огэ по математике / маттаймСкачать
ОГЭ. Задача на описанную окружность № 16. Как легко решить задачуСкачать
Геометрия. ОГЭ по математике. Задание 16Скачать
НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать
Геометрия. ОГЭ по математике. Задание 16Скачать
Задание 9 ОГЭ от ФИПИСкачать
ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать
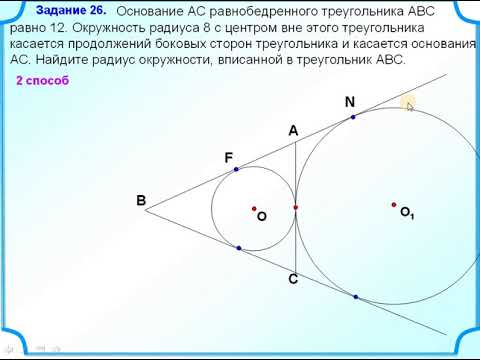
ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать
Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать
