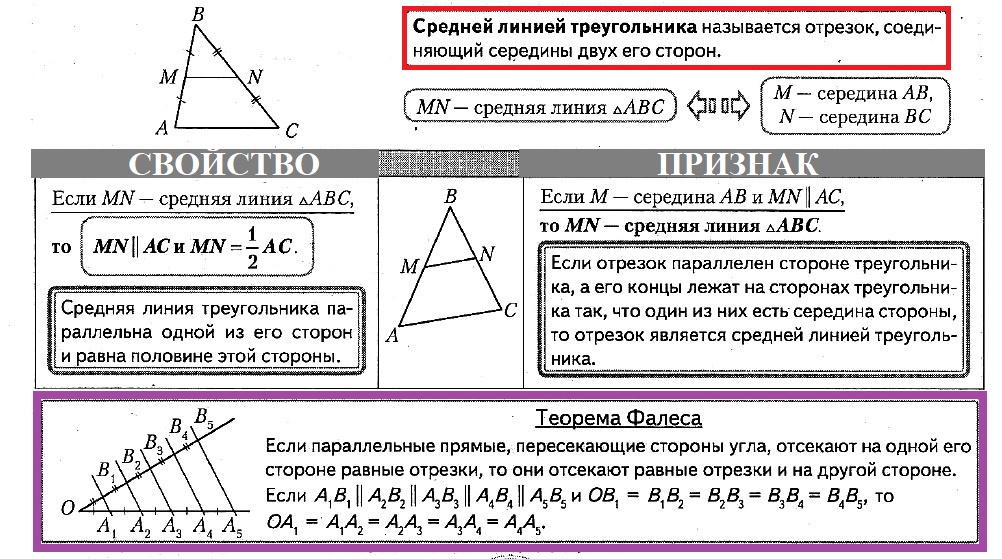
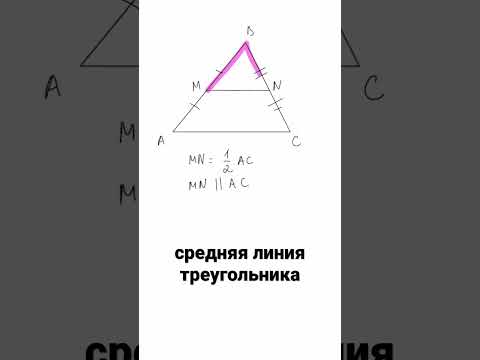
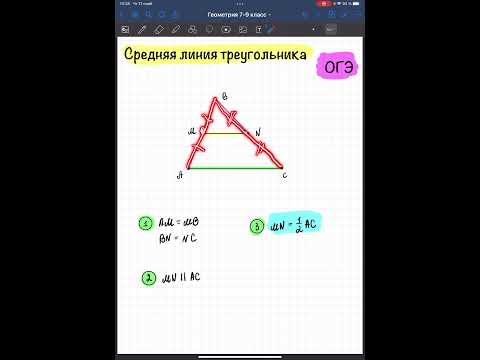
Средняя линия треугольника огэ

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника:
1. Средняя линия параллельна третьей стороне и равна ее половине.
2. Средняя линия трeугольника отсекает от него треугольник, подобный данному (с коэффициентом подобия 1/2 ).
3. Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия 1/2.

Свойство средней линии треугольника является следствием теоремы Фалеса.

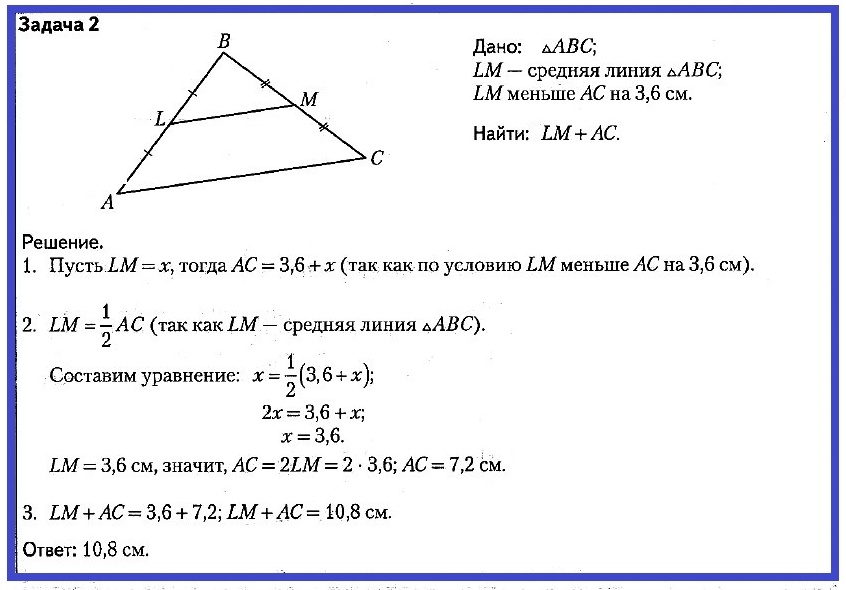
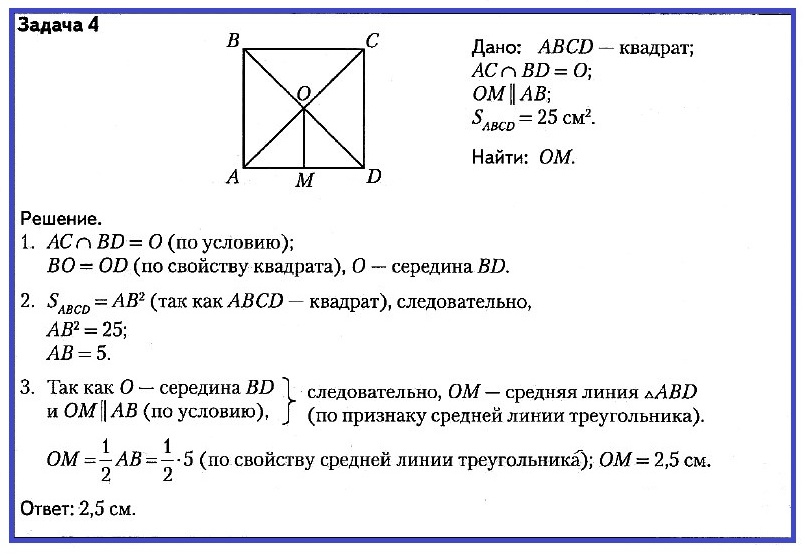
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

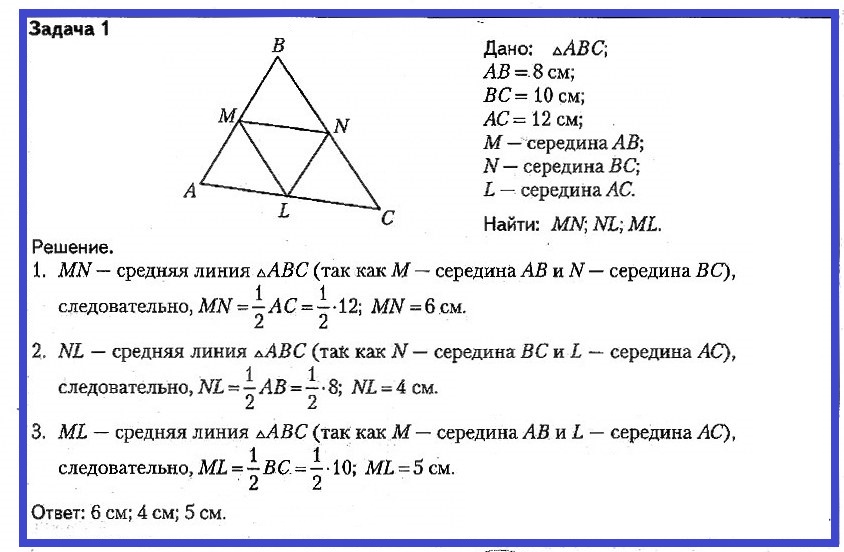
Задача № 1. Дано: ΔABC; AB = 8 см; BC = 10 см; AC = 12 см; M — середина AB; N — середина BC; L — середина AC. Найти: MN, NL, ML.

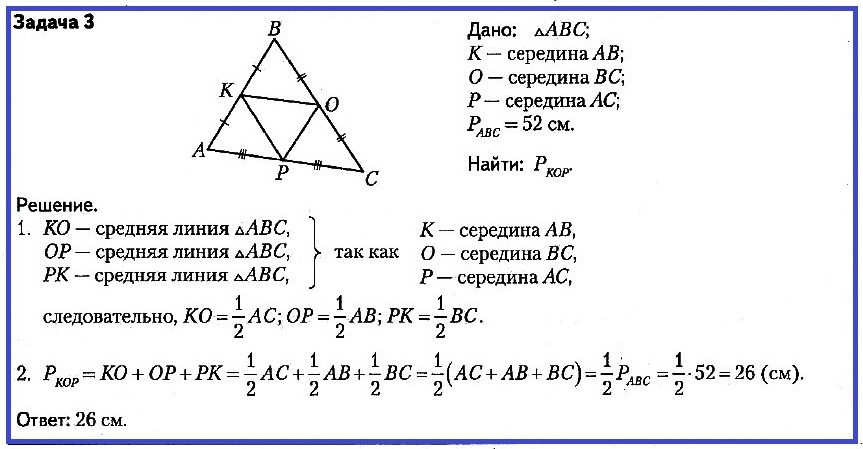
Задача № 3. ΔABC; K — середина AB; O — середина BC; P — середина AC; P_ABC = 52 см. Найти: P_КOР

Это конспект по теме «Средняя линия треугольника + Задачи по теме». Выберите дальнейшие действия:

Задачи по теме:»Средняя линия треугольника» 8 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

1.Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.

2. В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.

3.В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.

4.Периметр равностороннего треугольника АВС равен 24 см. Найдите длину средней линии этого треугольника.

5.Стороны треугольника равны 2 см, 3 см и 4 см. Его вершины являются серединами сторон второго треугольника. Найдите периметр второго треугольника.

6.Периметр треугольника равен 12 см, середины сторон соединены отрезками. Найдите периметр получившегося треугольника.

7.Периметр равностороннего треугольника равен 72 см. Найдите его среднюю линию.

8.Периметр треугольника равен 12 см. Найдите периметр треугольника, отсекаемого от данного какой-нибудь его средней линией.

9.Средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. Найдите стороны треугольника, если его периметр равен 16 см.

10.Через вершины треугольника проведены прямые, параллельные его противоположным сторонам. Найдите периметр треугольника, ограниченного этими прямыми, если периметр исходного треугольника равен 6 см.

11.В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 9. Найдите площадь треугольника ABC.

12.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 45. Найдите площадь треугольника ABC.

13.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 94. Найдите площадь треугольника ABC.

14.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 7. Найдите площадь треугольника ABC.

15.В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.

16.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC.

17.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.

18.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 21. Найдите площадь треугольника ABC.

19.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 89. Найдите площадь треугольника ABC.

20.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC.

21.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 96. Найдите площадь треугольника ABC.

22.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 57. Найдите площадь треугольника ABC.

23.На клетчатой бумаге с размером клетки 1х1 изображён треугольник . Найдите длину его средней линии, параллельной стороне .

Презентация «Подготовка к ОГЭ. Модуль «Геометрия». Средняя линия треугольника. Средняя линия трапеции.»

Презентация «Подготовка к ОГЭ. Модуль «Геометрия». Средняя линия треугольника. Средняя линия трапеции.» позволяет повторить основные понятия тем и вспомнить решения ключевых задач. В презентации предусмотрены небольшие тестовые работы. Все рассматриваемые задания взяты из открытого банка заданий ОГЭ.

Просмотр содержимого документа
«Презентация «Подготовка к ОГЭ. Модуль «Геометрия». Средняя линия треугольника. Средняя линия трапеции.»»

Средняя линия треугольника.

Средняя линия трапеции.

МБОУ СОШ № 43 г. Новосибирска

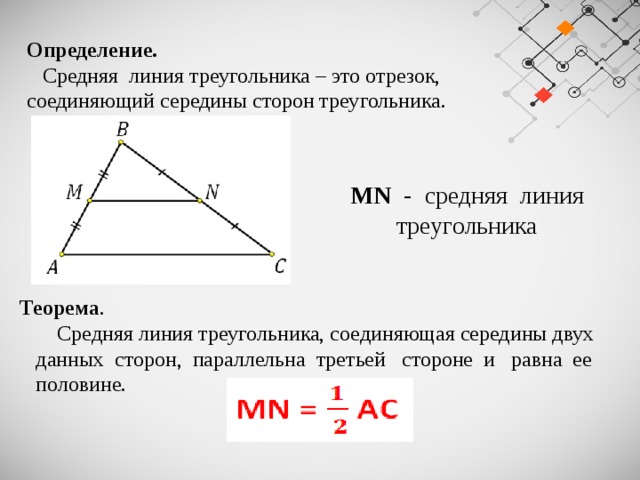
Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.

MN — средняя линия треугольника

Средняя линия треугольника, соединяющая середины двух

данных сторон, параллельна третьей стороне и равна ее

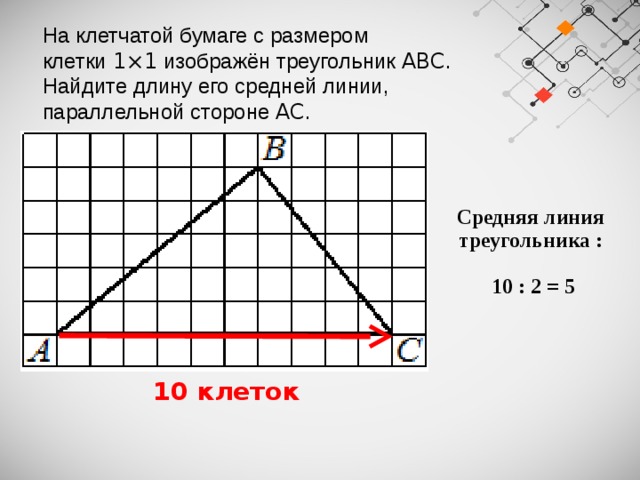
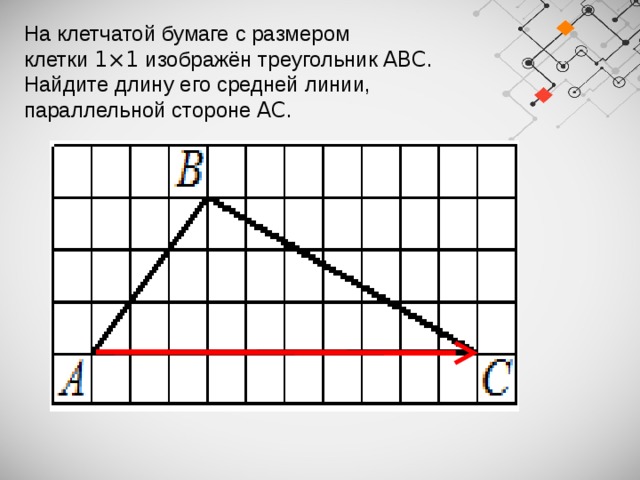
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC .

Найдите длину его средней линии,

параллельной стороне AC .

Средняя линия треугольника :

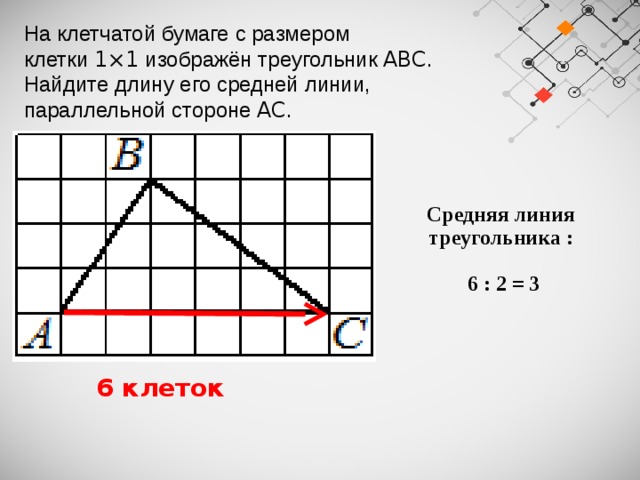
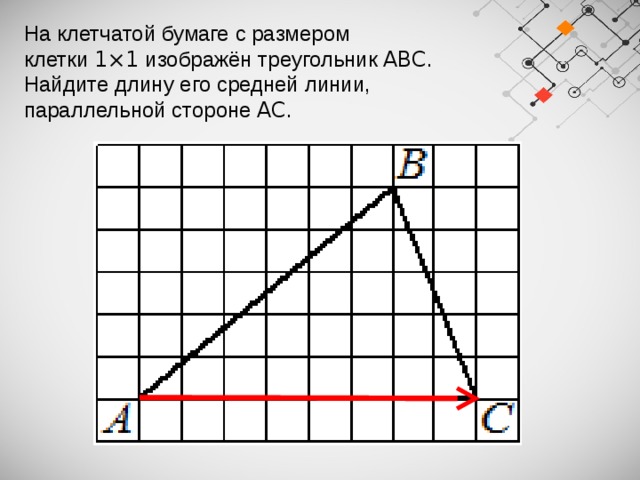
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .

Средняя линия треугольника :

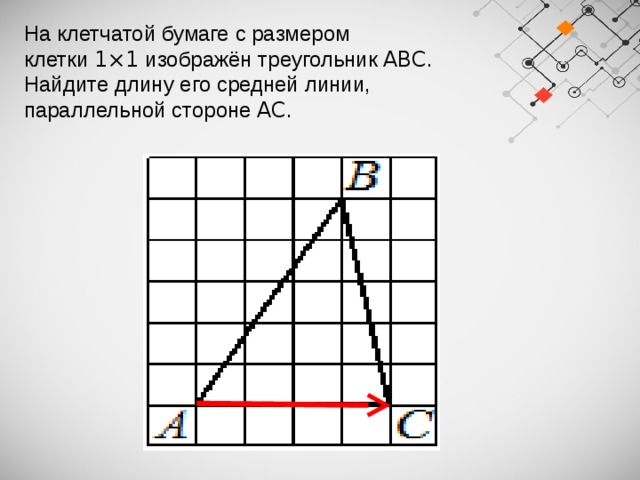
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .

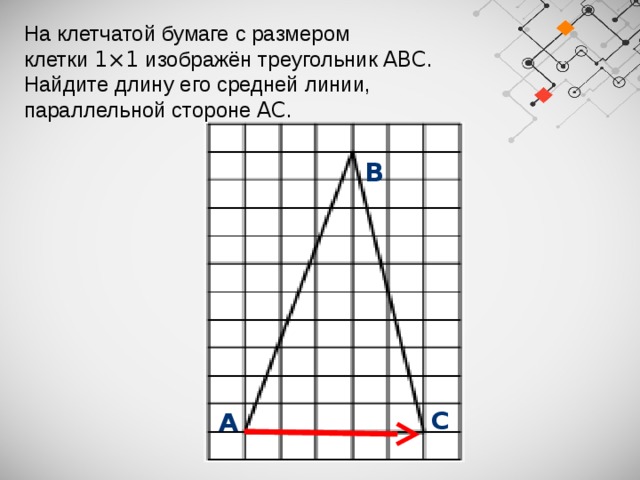
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .

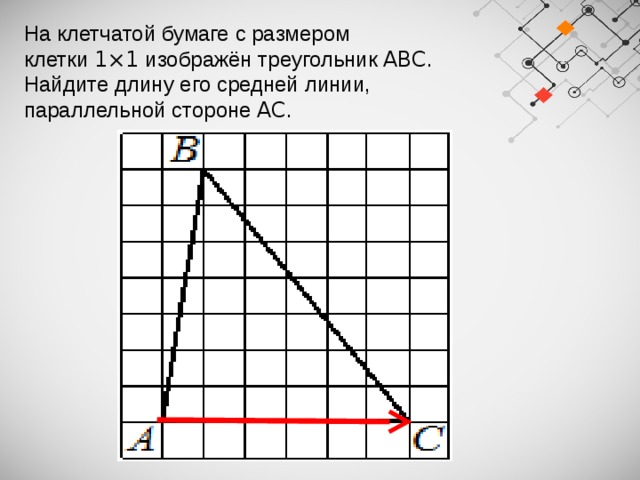
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .

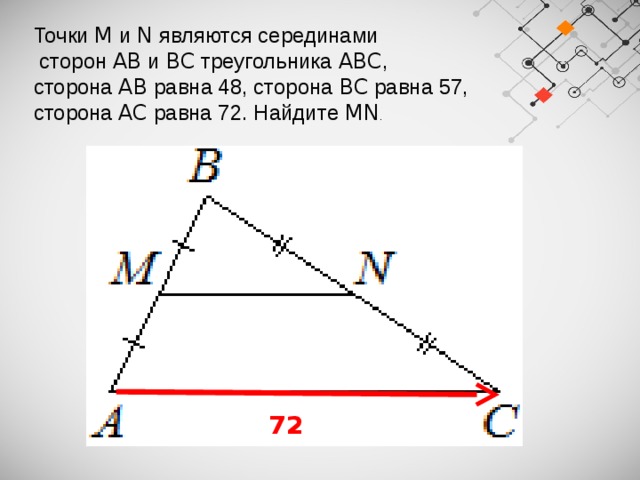
Точки M и N являются серединами

сторон AB и BC треугольника ABC ,

сторона AB равна 48, сторона BC равна 57,

сторона AC равна 72. Найдите MN .

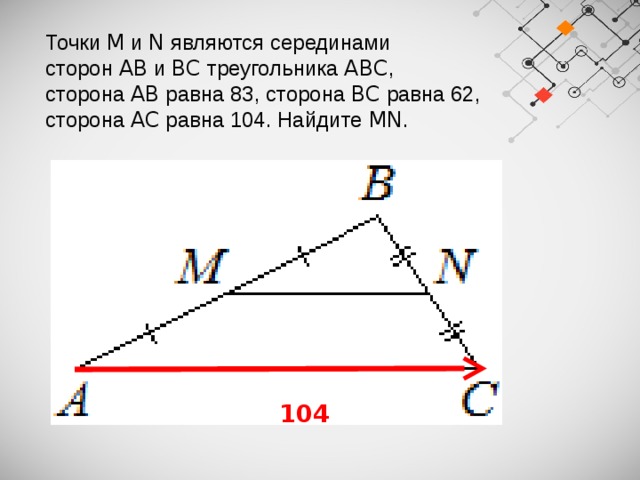
Точки M и N являются серединами сторон AB и BC треугольника ABC ,

сторона AB равна 83, сторона BC равна 62, сторона AC равна 104. Найдите MN .

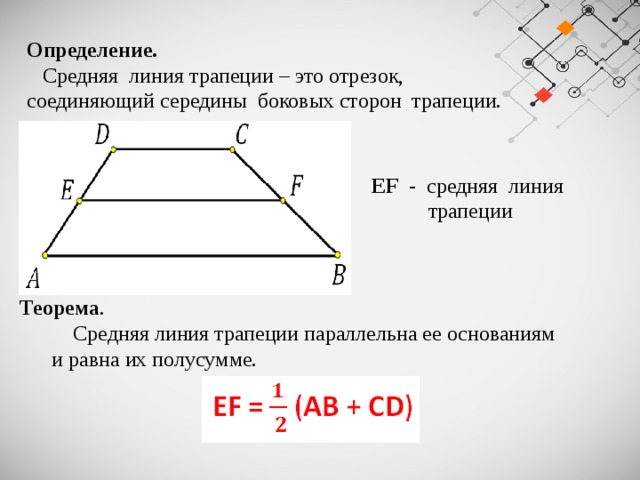
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции.

EF — средняя линия

Средняя линия трапеции параллельна ее основаниям

и равна их полусумме.

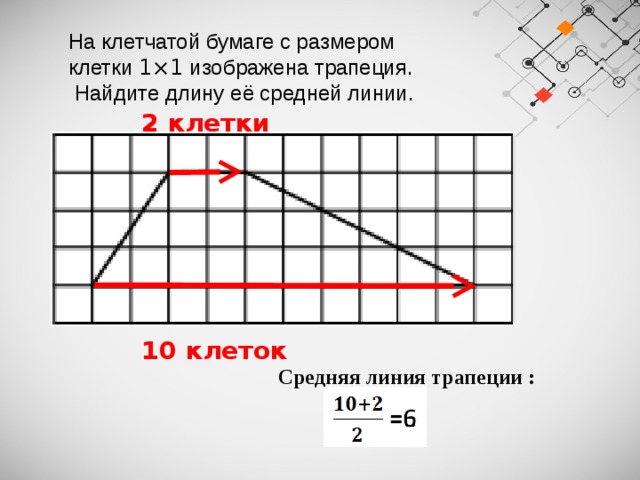
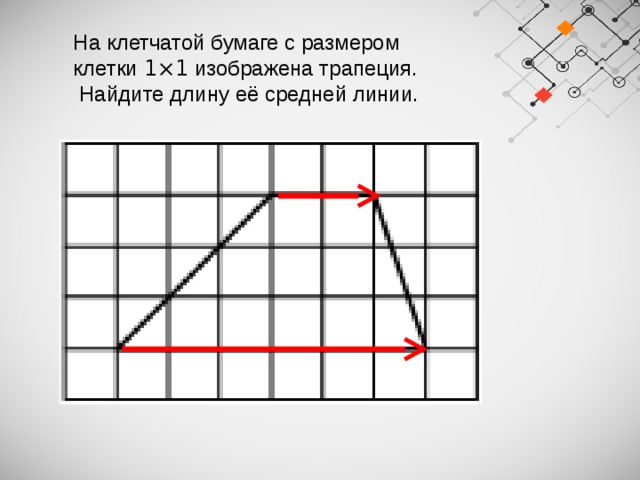
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.

Найдите длину её средней линии.

Средняя линия трапеции :

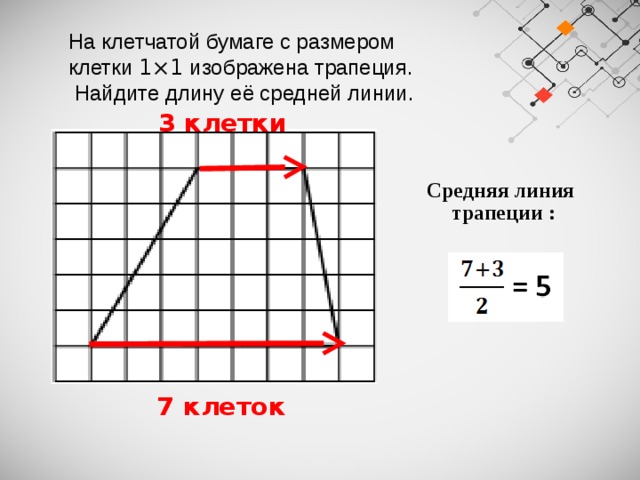
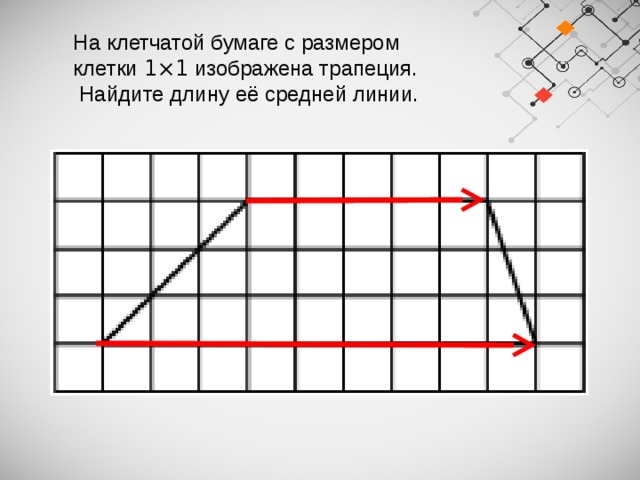
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.

Найдите длину её средней линии.

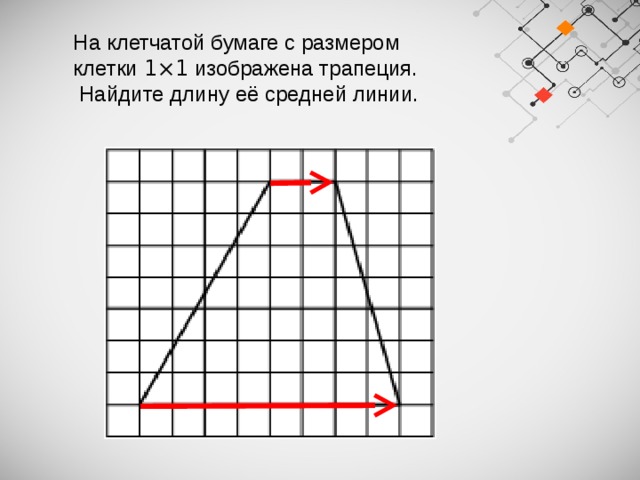
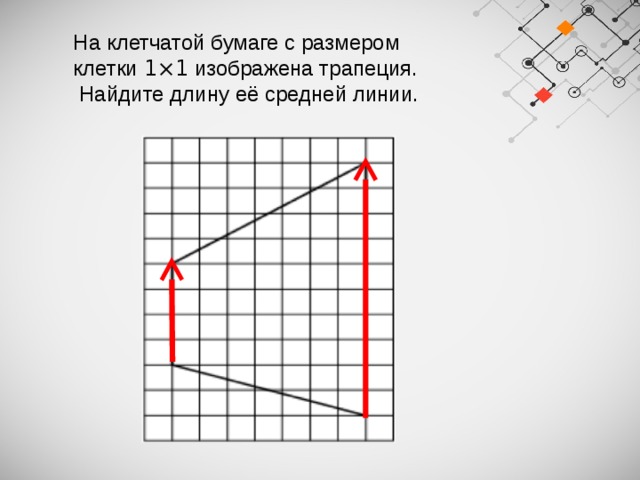
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.

Найдите длину её средней линии.

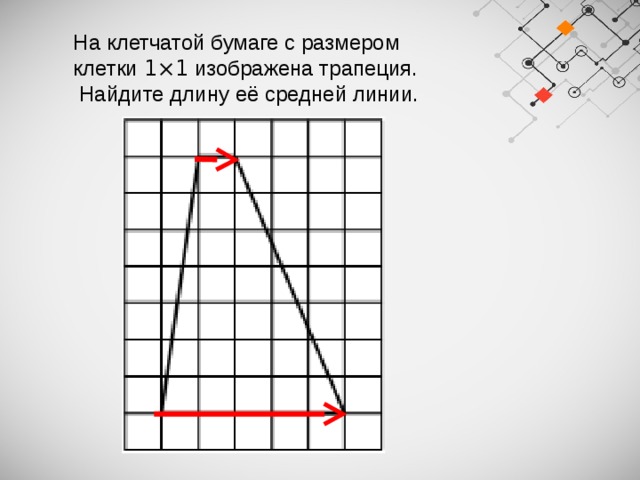
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.

Найдите длину её средней линии.

На клетчатой бумаге с размером клетки 1×1 изображена трапеция.

Найдите длину её средней линии.

На клетчатой бумаге с размером клетки 1×1 изображена трапеция.

Найдите длину её средней линии.

На клетчатой бумаге с размером клетки 1×1 изображена трапеция.

Найдите длину её средней линии.

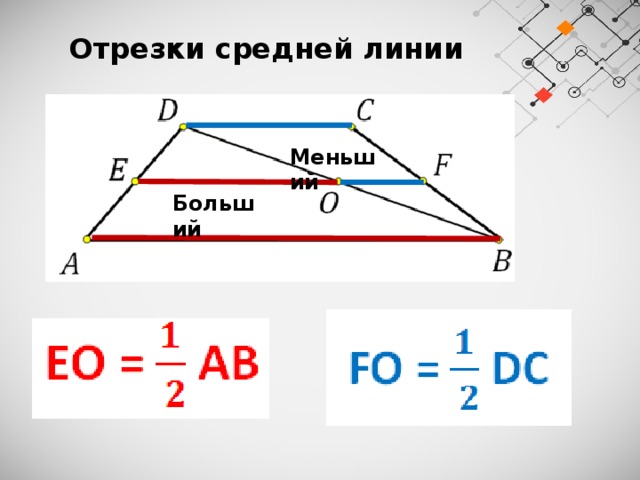
Отрезки средней линии

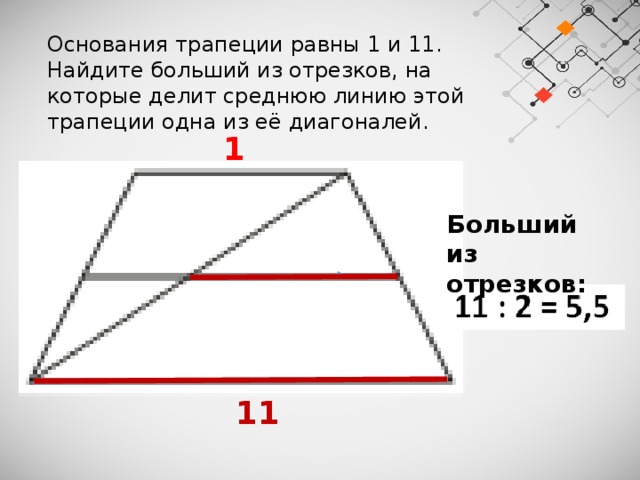
Основания трапеции равны 1 и 11.

Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Больший из отрезков:

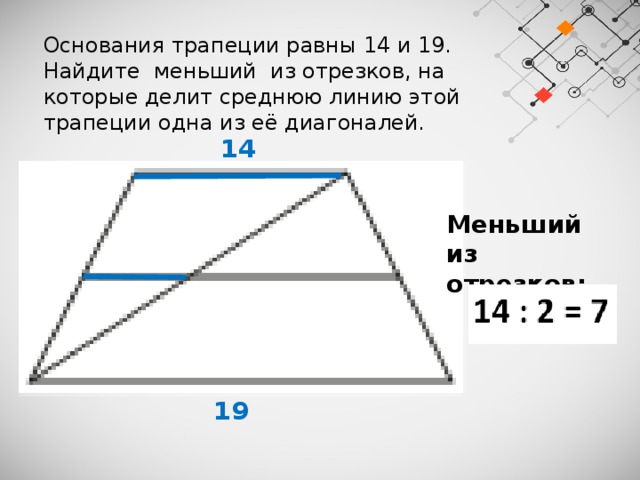
Основания трапеции равны 14 и 19.

Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

Меньший из отрезков:

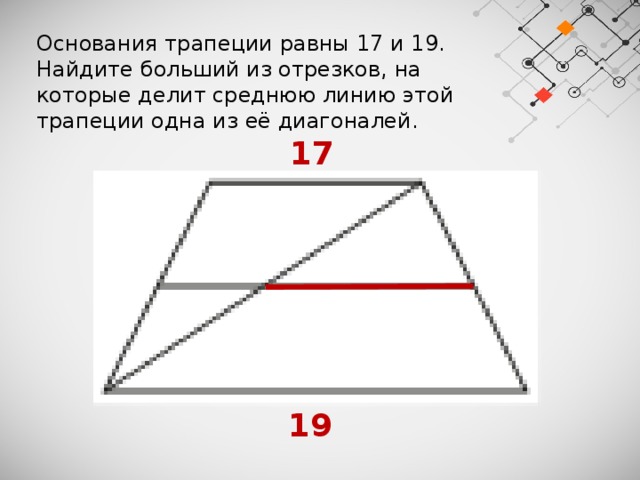
Основания трапеции равны 17 и 19.

Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

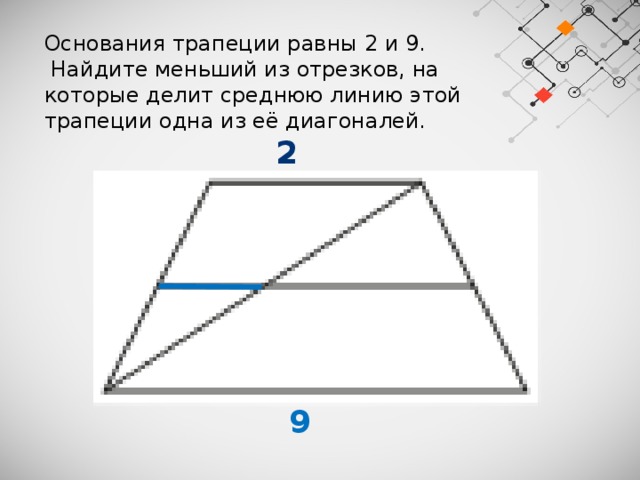
Основания трапеции равны 2 и 9.

Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

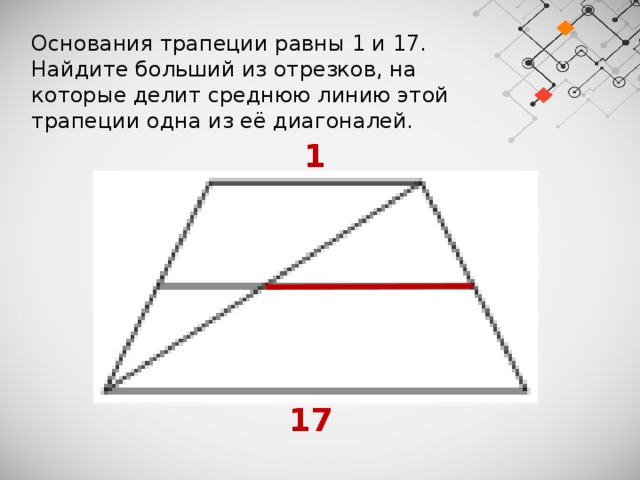
Основания трапеции равны 1 и 17.

Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

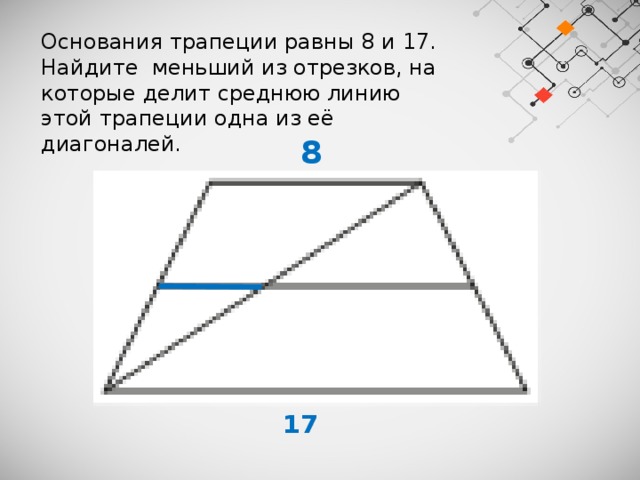
Основания трапеции равны 8 и 17.

Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.