Средний геометрический радиус окружностей

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. 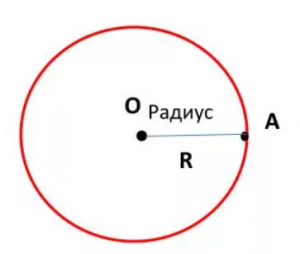Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

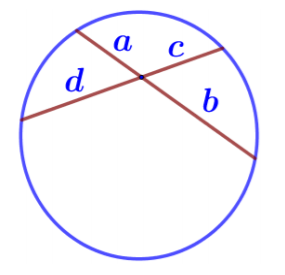
Свойство хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Дуга, касательная, круг, сектор, сегмент

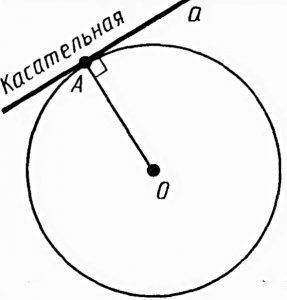
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

Свойства касательной

На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

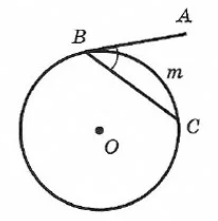
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

Сектор и его площадь

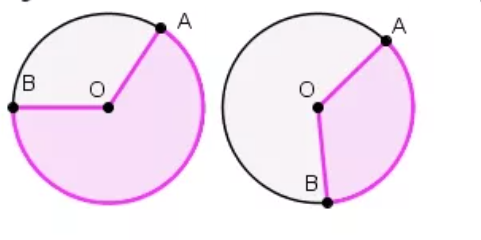
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.

Радиус и диаметр окружности

Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).

Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.

Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности

Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.

Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.

На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;

Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.

Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.

Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.

Формула радиуса окружности через диаметр:

Формула диаметра окружности через радиус:

Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.

Существует радиус вписанной окружности
и радиус описанной окружности.

Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.

Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.

Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.

Радиус — что это такое и как найти радиус окружности

Через длину стороны

Формула для нахождения длины окружности через радиус:

, где r — радиус окружности.

Найти радиус круга, зная окружность

Окружность круга PРезультат

Радиус и диаметр

Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.

А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:

Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.

Обозначается диаметр также первой буквой своего слова – D или d.

Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.

Длина диаметра равна удвоенной длине радиуса.

Вычисление радиуса

Радиус можно посчитать разными способами.

Если известен диаметр

Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.

Если известна длина окружности круга

Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.

Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:

Означает данное значение отношение длины окружности к диаметру той же окружности.

Если известна площадь круга

Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:

В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.

Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.

Способ расчета радиуса круга:

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14

Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

• r — искомый радиус окружности.
• a — сторона описанного квадрата.

Как посчитать радиус зная длину окружности

Чему равен радиус (r) если длина окружности C?

Формула

r = C /_2π , где π ≈ 3.14

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

1. Радиус составляет половину диаметра. Это мы продемонстрировали только что.
2. У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

Радиус, который перпендикулярен хорде, делит ее на две равные части.

Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

По площади сектора и центральному углу

• Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем

В случае, когда величина α выражена в в радианах , получаем

Формулы для площади круга и его частей

,

где R – радиус круга, D – диаметр круга

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Числовая характеристика	Рисунок	Формула
Площадь круга
Площадь сектора
		Площадь сегмента

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Центральный угол, вписанный угол и их свойства

Связанные определения

• Центральный угол в окружности — это угол , образованный двумя радиусами.
• Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .

В случае, когда величина α выражена в градусах , справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах , справедлива пропорция

из которой вытекает равенство:

Уравнение окружности

r 2 = ( x – a ) 2 + ( y – b ) 2

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:

<	x = a + r cos t
	y = b + r sin t

Углы между двумя хордами

Случай 1: два секущие пересекаются внутри окружности.

Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.

Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

• r — искомый радиус окружности.
• S — площадь треугольника.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

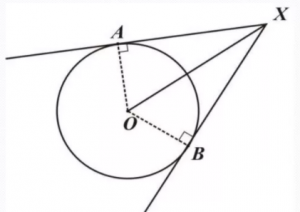
Основные свойства касательных к окружности

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

Обобщения

Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

• R — искомый радиус окружности.
• d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
• a, b — стороны вписанного прямоугольника.

Площадь круга, онлайн расчет

Как найти площадь круга по формуле через радиус либо диаметр круга.Площадь круга, онлайн расчет

Вместо заключения

Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.

Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.