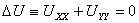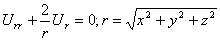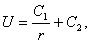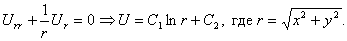Среднее значение на окружности (3 видео)

Лекция 7. Гармонические функции и их свойства

Рассмотрим уравнение Лапласа на плоскости

и в пространстве

Уравнение (33) при переходе к полярным координатам преобразуется к виду

Рис 14 Рис 14.1

Если в пространстве перейти к сферическим координатам

то уравнение (34) примет вид

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (33) или (34) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных — круговой) симметрией.

Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения

Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим

где C₁ и C₂ — произвольные постоянные. Полагая C₁=1, C₂=0, получим функцию

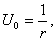
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U₀ является гармонической всюду в пространстве, кроме начала координат 0.

Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:

Выбирая С₁=-1 и С₂=0, будем иметь функцию

Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q , помещенным в начало координат. Тогда потенциал этого поля равен

Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен

где q₁ — линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).

Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.

Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (х_o,у_o) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть

При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)

Если в этой формуле положить ρ=0, то получится формула (35).

Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 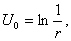(см. рис.15.1):

Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:

где D — круг радиуса R. Разделив обе части полученного равенства на R 2 /2 , будем иметь

В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.

Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (х_о, у_о), то эта функция гармоническая в D. Из формулы (37) получается:

Следствие. Если функция U=U(x,y) гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге ,то

Число называют нормой функции U=U(x,y) в области D , и неравенство (38) можно переписать в виде

Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:

Применим это неравенство к формуле (37):

Что и требовалось доказать.

Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.

Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (x_o, у_o) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству

Из неравенства Харнака следует теорема Лиувилля.

Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.

Доказательство. Если функция U=U(x, у) ограничена сверху, то U₁=-U(x, y) — ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: Более того, можно считать, что M=0. Действительно, ,а разность (U-M) тоже гармоническая функция. Итак, предполагая существование гармонической во всей плоскости неотрицательной функции U(x, у), мы докажем, что эта функция постоянная.

Воспользуемся неравенством Харнака

Если функция U(x, у) гармоническая во всей плоскости то, фиксировав произвольное и неограниченно увеличивая R мы получим

то есть Теорема Лиувилля доказана.

Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.

Терема о среднем. Пусть функция U=U(x, у) гармоническая в некотором шаре D радиуса R c центром
(x_o , у_o , z_o ) и непрерывная в соответствующем замкнутом шаре Тогда значение этой функции в центре шара равно:

а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть

б) ее среднему значению в шаре D, то есть

Содержание

Среднее геометрическое чисел
Расчет среднего геометрического
Пример задачи
Как вы вычисляете среднее значение набора круговых данных?
29 ответов
📹 Видео

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Среднее геометрическое чисел

В данной публикации мы рассмотрим, с помощью какой формулы можно найти среднее геометрическое чисел, а также разберем примеры задач для ее демонстрации на практике.

Видео:Как искать точки на тригонометрической окружности.Скачать

Расчет среднего геометрического

Чтобы вычислить среднее геометрическое двух или более чисел, требуется их перемножить, а затем из полученного результата извлечь корень, степень которого равняется их количеству.

Допустим, у нас есть числа . Среднее геометрическое находится по формуле:

Частные случаи формулы:

Количество чиселФормула2

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value="» data-order=»«> 3

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value="» data-order=»«> 4

Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Пример задачи

Задание 1
Найдем среднее геометрическое чисел 3, 6 и 12.

Решение:
Воспользуемся соответствующей формулой для трех чисел:

Задание 2
Среднее геометрическое четырех чисел равняется 4, а также известны три из них – 2, 2 и 4. Найдем четвертое.

Решение:
Обозначим число, которое требуется найти буквой x . Формула выглядит следующим образом:

Помещаем число 4 под знак корня, сохранив равенство (для этого возводим его в четвертую степень, т.е. ):

Видео:Тригонометрическая окружность. Как выучить?Скачать

Как вы вычисляете среднее значение набора круговых данных?

Я хочу рассчитать среднее значение набора круговых данных. Например, у меня может быть несколько образцов показаний компаса. Проблема, конечно, в том, как справиться с оберткой. Тот же алгоритм может быть полезен и для циферблата.

фактический вопрос сложнее-что означает статистика на сфере или в алгебраическом пространстве, которое «обертывается», например, аддитивная группа mod n. Ответ может быть не уникальным, например, среднее значение 359 градусов и 1 степени может быть 0 градусов или 180, но статистически 0 выглядит лучше.

Это реальная проблема программирования для меня, и я пытаюсь сделать так, чтобы это не выглядело как просто математическая проблема.

Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

29 ответов

вычислить единичные векторы по углам и взять угол их среднего значения.

этот вопрос подробно рассматривается в книге: «Статистика сфер», Джеффри С. Уотсон, лекция Университета Арканзаса Заметки в математических науках, 1983 John Wiley & Sons, Inc. как упоминалось в http://catless.ncl.ac.uk/Risks/7.44.html#subj4 Брюс Карш.

хороший способ оценить средний угол, A, из набора угловых измерений a[i] 0

метод, заданный starblue, вычислительно эквивалентен, но его причины понятнее и, вероятно, программно более эффективны, а также хорошо работают в нулевом случае, так что слава ему.

предмет теперь исследуется более подробно Википедии, и с другими пользами, как частичные части.

Я вижу проблему — например, если у вас есть угол 45′ и угол 315′, «естественное» среднее будет 180′, но значение, которое вы хотите, на самом деле 0′.

Я думаю, что Starblue на что-то. Просто вычислите декартовые координаты (x, y) для каждого угла и добавьте эти результирующие векторы вместе. Угловое смещение конечного вектора должно быть вашим требуемым результатом.

я игнорирую сейчас, что направление компаса начинается с севера и идет по часовой стрелке, тогда как «нормальные» декартовые координаты начинаются с нуля вдоль оси X, а затем идут против часовой стрелки. Математика должна работать одинаково независимо.

ДЛЯ ЧАСТНОГО СЛУЧАЯ ДВУХ УГЛОВ:

ответ ((a + b) mod 360) / 2 is неправильно. Для углов 350 и 2 ближайшая точка равна 356, а не 176.

единичный вектор и тригонометрические решения могут быть слишком дорогими.

то, что я получил от немного возиться:

0, 180 -> 90 (два ответа на это: это уравнение принимает ответ по часовой стрелке от a)
180, 0 -> 270 (см. выше)
180, 1 -> 90.5
1, 180 -> 90.5
20, 350 -> 5
350, 20 -> 5 (все следующие примеры обратного тоже правильно)
10, 20 -> 15
350, 2 -> 356
359, 0 -> 359.5
180, 180 -> 180

ackb прав, что эти векторные решения не могут считаться истинными средними углов, они являются только средним из единичных векторных аналогов. Однако предлагаемое решение ackb не кажется математически обоснованным.

ниже приводится решение, которое математически выведено из цели минимизации (угол[i] — avgAngle)^2 (где разница корректируется при необходимости), что делает его истинным арифметическим средним углов.

во-первых, мы нужно посмотреть, в каких именно случаях разница между углами отличается от разницы между их нормальными числовыми аналогами. Рассмотрим углы x и y, если y >= x — 180 и y

вот изображение, демонстрирующее, где возникают проблемы при вычислении разностей углов. Если x лежит в серой области, то будет проблема.

чтобы минимизировать переменную, в зависимости от кривой, мы можем взять производную от того, что мы хотим минимизировать, а затем найти поворотную точку (где производная = 0).

здесь мы применим идею минимизации квадратной разности для получения общей формулы среднего арифметического: sum (a[i])/n. Кривая y = sum ((a[i]-x)^2) может быть минимизирована следующим образом:

Теперь применяя его к кривым с нашими скорректированными различиями:

b = подмножество a, где правильная (угловая) разность a[i] — x c = подмножество a, где правильная (угловая) разность (a[i]-360) — x cn = размер c d = подмножество a, где правильная (угловая) разность (a[i]+360) — x dn = размер d

этого недостаточно, чтобы получить минимум, в то время как он работает для нормальных значений, который имеет неограниченный набор, поэтому результат определенно будет находиться в диапазоне набора и поэтому действителен. Мы нужен минимум в пределах диапазона (определенного сегментом). Если минимум меньше нижней границы нашего сегмента, то минимум этого сегмента должен быть на нижней границе (потому что квадратичные кривые имеют только 1 поворотную точку), и если минимум больше верхней границы нашего сегмента, то минимум сегмента находится на верхней границе. После того, как у нас есть минимум для каждого сегмента, мы просто находим тот, который имеет наименьшее значение для того, что мы минимизируем (sum ((b[i] — x)^2) + sum(((c[i]-360)-b)^2) +sum(((d[i] + 360)-c)^2)).

вот изображение кривой, которое показывает, как она изменяется в точках, где x=(a[i]+180)%360. Набор данных в вопрос .

вот реализация алгоритма на Java, включая некоторые оптимизации, его сложность составляет O (nlogn). Его можно уменьшить до O (n), если заменить сортировку на основе сравнения сортировкой, не основанной на сравнении, такой как radix род.

среднее арифметическое множества углов может не совпадать с вашим интуитивным представлением о том, каким должно быть среднее. Например, среднее арифметическое множества равно 216 (и 144). Ответ, который вы сразу подумаете, вероятно, 180, однако хорошо известно, что среднее арифметическое сильно зависит от значений ребер. Вы также должны помнить, что углы не являются векторами, как это может показаться привлекательным при работе с углами иногда.

этот алгоритм, конечно, также применяется ко всем величинам, которые подчиняются модульной арифметике (с минимальной регулировкой), например, времени суток.

Я также хотел бы подчеркнуть, что, хотя это истинное среднее углов, в отличие от векторных решений, это не обязательно означает, что это решение, которое вы должны использовать, среднее значение соответствующих единичных векторов вполне может быть значением, которое вы на самом деле должны использовать.

вы должны определить в среднем более точно. Для конкретного случая двух углов я могу придумать два разных сценария:

» истинное » среднее значение, т. е. (a + b) / 2% 360.
угол, который указывает «между» двумя другими, оставаясь в том же полукруге, например, для 355 и 5, это будет 0, а не 180. Для этого нужно проверить, больше ли разница между двумя углами 180 или нет. Если это так, увеличьте меньший угол на 360 перед использованием приведенной выше формулы.

Я не вижу, как вторая альтернатива может быть обобщена для случая более двух углов.

Как и все средние, ответ зависит от выбора метрики. Для заданной метрики M среднее некоторых углов a_k в [- pi,pi] для k в [1,N] является тем углом a_M, который минимизирует сумму квадратов расстояний d^2_M(a_M, a_k). Для средневзвешенного значения в сумму просто входят веса w_k (такие, что sum_k w_k = 1). То есть,

a_M = arg min_x sum_k w_k d^2_M (x,a_k)

двумя общими вариантами метрики являются метрики Фробениуса и Римана. Для Метрика Фробениуса, существует прямая формула, соответствующая обычному понятию среднего подшипника в круговой статистике. См.» средства и усреднение в группе ротаций», Maher Moakher, SIAM Journal on Matrix Analysis and Applications, Volume 24, Issue 1, 2002, подробнее.
http://link.aip.org/link/?SJMAEL/24/1/1

вот функция для GNU Octave 3.2.4, которая выполняет вычисления:

Я хотел бы поделиться методом, который я использовал с микроконтроллером, который не имел возможности с плавающей запятой или тригонометрии. Мне все еще нужно было «усреднить» 10 сырых показаний подшипника, чтобы сгладить изменения.

проверьте, является ли первый подшипник диапазоном 270-360 или 0-90 градусов (северные два квадранта)
если это так, поверните это и все последующие показания на 180 градусов, сохраняя все значения в диапазоне 0
после того, как 10 показаний были взяты вычислить числовое среднее, предполагая, что не было обертки
если вращение на 180 градусов действовало, то поверните рассчитанное среднее значение на 180 градусов, чтобы вернуться к «истинному» подшипнику.

Это не идеально; он может сломаться. В этом случае мне это сошло с рук, потому что устройство вращается очень медленно. Я поставлю его там, на случай, если кто-то еще обнаружит, что работает под подобное ограничение.

вот полное решение: (входной сигнал массив подшипника в градусах (0-360)

Я бы пошел векторным путем, используя комплексные числа. Мой пример в Python, который имеет встроенные комплексные числа:

обратите внимание, что Python не нужно чтобы создать временный новый список векторов, все вышеперечисленное можно сделать за один шаг; я просто выбрал этот способ приблизить псевдо-код, применимый к другим языкам.

вот полное решение C++:

Он принимает углы в виде вектора двойников и возвращает среднее значение просто как двойник. Углы должны быть в градусах, и, конечно, среднее значение также в градусах.

в python, с углами между [-180, 180)

в среднем два угла есть два средних 180° друг от друга, но мы можем ближе средний.

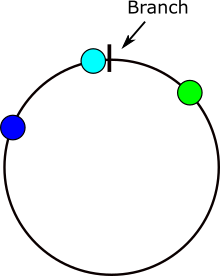
визуально, среднее значение синего (b) и зеленый (a) дает точку чирок:

углы «обернуть» (например, 355 + 10 = 5), но стандартная арифметика проигнорирует это точка ветвления. Однако если угол b находится напротив точки ветви, тогда (b + g) / 2 дает ближайшую среднюю: точку чирок.

для любых двух углов мы можем повернуть задачу так, чтобы один из углов был противоположен точке ветви, выполнить стандартное усреднение, а затем повернуть назад.

вот идея: постройте среднее итеративно, всегда вычисляя среднее значение углов, которые ближе всего друг к другу, сохраняя вес.

еще одна идея: найти наибольший зазор между заданными углами. Найдите точку, которая делит его пополам, а затем выберите противоположную точку на окружности в качестве опорного нуля для вычисления среднего.

обозначим эти углы с точками на окружности.

можем ли мы предположить, что все эти точки попадают на одну и ту же половину круга? (В противном случае нет очевидного способа определить «средний угол». Подумайте о двух точках на диаметре, например, 0 град и 180 град — — — это средний 90 град или 270 град? Что происходит, когда у нас есть 3 или более равномерного распределения точек?)

с этим предположением, мы выбираем произвольную точку на полуокружности как «начало координат «и измеряют данный набор углов относительно этого начала координат (назовем это»относительным углом»). Обратите внимание, что относительный угол имеет абсолютное значение строго меньше 180 градусов. Наконец, возьмите среднее из этих относительных углов, чтобы получить желаемый средний угол (относительно нашего происхождения, конечно).

нет единого «правильного ответа». Рекомендую почитать книгу, К. В. Mardia и П. Е. Юпп, «курсовую по статистике», (М., 1999), для тщательного анализа.

Alnitak имеет правильное решение. Решение Ника Фортескью функционально то же самое.

для частного случая где

(sum(x_component) = 0.0 && sum (y_component) = 0.0 ) // например, 2 угла 10. и 190. степени ЕА.

используйте 0.0 градусов в качестве суммы

вычислительно вы должны проверить для этого случая, так как atan2 (0. , 0.) не определено и будет генерировать ошибку.

средний угол phi_avg должен иметь свойство, что sum_i|phi_avg-phi_i / ^2 становится минимальным, где разница должна быть в [-Pi, Pi) (потому что это может быть короче, чтобы идти в другую сторону!). Это легко достигается путем нормализации всех входных значений до [0, 2Pi), сохранения среднего значения phi_run и выбора нормализации / phi_i-phi_run / to [- Pi,Pi) (путем добавления или subtractin 2Пи). Большинство предложений выше делают что-то еще, что делает не имейте это минимальное свойство, то есть они средние что-то, но не углы.

на английском языке:

сделайте второй набор данных со всеми углами, сдвинутыми на 180.
возьмите дисперсию обоих наборов данных.
возьмите среднее значение набора данных с наименьшей дисперсией.
если это среднее значение из сдвинутого набора, то сдвиньте ответ снова на 180.

массив углов #numpy NX1

(просто хочу поделиться своей точкой зрения из теории оценки или статистического вывода)

Проворный испытание, чтобы получить ММСЕ^ оценка углы, но это один из вариантов, чтобы найти «усредненное» направлении; можно также найти MMAE^ оценка, или некоторые другие оценки «усредненной» направление, и это зависит от Метрики количественной оценки погрешности направлении; или в более общем плане теория оценивания, определение функции затрат.

^ MMSE/MMAE соответствует минимальная средняя квадратная / абсолютная ошибка.

ackb сказал: «средний угол phi_avg должен иметь свойство, что sum_i|phi_avg-phi_i / ^2 становится минимальным. они усредняют что-то, но не углы»

— — — — — вы количественно оцениваете ошибки в среднем квадрате, и это один из наиболее распространенных способов, однако, не единственный способ. Ответ, который предпочитает большинство людей здесь (т. е. сумма единичных векторов и получить угол результата), на самом деле является одним из разумных решений. Это (может быть доказано) оценка ML, которая служит «усредненным» направлением, которое мы хотим, если направления векторов моделируются как распределение фон Мизеса. Это распределение не является причудливым и является просто периодически выборочным распределением из 2D Guassian. Увидеть Eqn По. (2.179) в книге Бишопа «распознавание образов и машинное обучение». Опять же, ни в коем случае это не единственное лучшее представление «среднего» направления, однако вполне разумное, которое имеет как хорошее теоретическое обоснование, так и простое реализация.

Nimble сказал: «ackb прав, что эти векторные решения не могут считаться истинными средними углов, они являются только средним значением единичных векторных аналогов»

—-Это не правда. «Единичные векторные аналоги»раскрывают информацию о направлении вектора. Угол-это величина без учета длины вектора, а единичный вектор-это что-то с дополнительной информацией о том, что длина равна 1. Вы можете определить свой «единичный» вектор должен быть длиной 2, это не имеет большого значения.

Я решил проблему с помощью ответа от @David_Hanak. Как он заявляет:

угол, который указывает «между» двумя другими, оставаясь в том же полукруге, например, для 355 и 5, это будет 0, а не 180. Для этого нужно проверить, больше ли разница между двумя углами 180 или нет. Если это так, увеличьте меньший угол на 360 перед использованием приведенной выше формулы.

Итак, что я сделал, это вычислить среднее значение всех угол. И тогда все углы, которые меньше этого, увеличить их на 360. Затем пересчитайте среднее значение, добавив их все и разделив их на длину.