Спираль прямая линия окружность

В первой экспериментальной установке отрицательно заряженная частица влетает в однородное электрическое поле так, что вектор скорости перпендикулярен вектору напряжённости электрического поля (рис. 1). Во второй экспериментальной установке вектор скорости такой же частицы параллелен индукции магнитного поля (рис. 2).

Установите соответствие между экспериментальными установками и траекториями движения частиц в них.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

А) в первой установке

Б) во второй установке

4) парабола

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

А) На частицу действует сила Кулона, она направлена перпендикулярно к начальной скорости частицы. Рассмотрим проекции скорости частицы на горизонтальную ось и ось, параллельную силовым линиям электрического поля. По горизонтальной оси скорость будет постоянной следовательно, координата Скорость по второй оси будет меняться по закону где a — ускорение создаваемое силой Кулона. Это движение подобно движению частицы в поле силы тяжести, значит, движение происходит по параболе.

Б) На частицу должна действовать сила Лоренца, но, в силу того, что скорость частицы параллельна линиям магнитного поля сила Лоренца будет равна нулю. Следовательно, скорость частицы не меняется и траектория её движения — прямая линия.

Видео:Построение эвольвенты окружностиСкачать

Рисование простых линий и фигур

Видео:Лекальные кривые. Спираль Архимеда. Эвольвента окружности. ЦиклоидаСкачать

Рисование прямых линий

Чтобы нарисовать один прямой отрезок линии, используйте инструмент «Отрезок линии». Обучающую игру с демонстрацией инструмента «Отрезок линии» см. в разделе Использование инструмента «Отрезок линии».

Выберите инструмент «Отрезок линии» .

Выполните одно из следующих действий:

Поместите указатель в ту точку, где должна начинаться линия, и перетащите его в точку ее окончания.

Щелкните в том месте, где должна начинаться линия. В диалоговом окне укажите значения длины и угла линии. Чтобы окрасить линию в текущий цвет заливки, выберите параметр Окрашивать отрезок в цвет заливки . Затем нажмите ОК .

Видео:Спираль Архимеда построениеСкачать

Рисование дуг

Нажмите и удерживайте инструмент «Отрезок линии» (). Выберите инструмент «Дуга» .

Выполните одно из следующих действий:

Поместите указатель в ту точку, где должна начинаться дуга, и перетащите его в точку ее окончания.

Щелкните в том месте, где должна начинаться дуга. Чтобы определить точку, из которой будет нарисована дуга, щелкните в диалоговом окне квадратик на локаторе неподвижной точки . После этого задайте любые из следующих параметров и нажмите кнопку ОК .

Длина по оси Х. Определяет ширину дуги.

Длина по оси Y. Определяет высоту дуги.

Тип. Определяет, каким контуром будет этот объект: замкнутым или открытым.

Вдоль. Определяет направление дуги. Выберите «Ось X» или «Ось Y» в зависимости от того, вдоль какой оси должна располагаться база дуги: горизонтальной (x) или вертикальной (y).

Наклон: определяет направление наклона дуги. Чтобы получить вогнутую дугу, введите отрицательное значение. Чтобы получить выгнутую дугу, введите положительное значение. При нулевом значении наклона получается прямая линия.

Окрашивать дугу в цвет заливки. Дуга окрашивается в текущий цвет заливки.

Примечание. Для динамического просмотра дуги по мере ввода параметров дважды щелкните инструмент «Дуга» на панели «Инструменты».

Видеоролик с инструкциями по использованию инструментов для рисования фигур см. в разделе Рисование основных фигур.

Видео:1 2 4 сопряжение окружностейСкачать

Рисование спиралей

Нажмите и удерживайте инструмент «Отрезок линии» ( ). Выберите инструмент «Спираль» .

Выполните одно из следующих действий:

Перетащите курсор, пока не получите спираль нужного размера. Чтобы повернуть спираль, перетащите указатель в дуге.

Щелкните в том месте, где должна начинаться спираль. В диалоговом окне задайте любые из следующих параметров и нажмите кнопку ОК .

Радиус. Определяет расстояние от центра до самой дальней точки спирали.

Рост. Определяет величину, на которую каждый виток спирали будет уменьшаться по сравнению с предыдущим витком.

Число сегментов. Определяет количество сегментов в спирали. Каждый полный виток спирали состоит из четырех сегментов.

Стиль. Определяет направление спирали.

Видеоролик с инструкциями по использованию инструментов для рисования фигур см. в разделе Рисование основных фигур.

Видео:Сопряжение прямой с окружностьюСкачать

Рисование сеток

Инструменты сеток используются для быстрого рисования прямоугольных и полярных сеток. Инструмент «Прямоугольная сетка» создает прямоугольные сетки заданного размера с заданным количеством разделителей. Инструмент «Полярная сетка» создает концентрические круги заданного размера с заданным количеством разделителей.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Рисование прямоугольных сеток

Нажмите и удерживайте инструмент «Отрезок линии» (). Выберите инструмент «Прямоугольная сетка» .

Выполните одно из следующих действий:

Перетащите курсор, пока не получите сетку нужного размера.

Щелкните, чтобы задать неподвижную точку сетки. Чтобы определить точку, из которой будет нарисована сетка, щелкните в диалоговом окне квадратик на локаторе неподвижной точки . После этого задайте любые из следующих параметров и нажмите кнопку ОК .

Размер по умолчанию. Определяет ширину и высоту всей сетки.

Горизонтальные разделители. Определяет количество горизонтальных разделителей между верхним и нижним краями сетки. Значение «Асимметрично» позволяет распределять горизонтальные разделители неравномерно с увеличением их частоты в сторону верхнего или нижнего края сетки.

Вертикальные разделители. Определяет количество вертикальных разделителей между левым и правым краями сетки. Значение «Асимметрично» позволяет распределять вертикальные разделители неравномерно с увеличением их частоты в сторону левого или правого края сетки.

Использовать внешний прямоугольник в качестве рамки. Заменяет верхний, нижний, левый и правый сегменты отдельным прямоугольным объектом.

Окрашивать сетку в цвет заливки. Сетка окрашивается в текущий цвет заливки (в противном случае заливка не задается).

Видео:Построение спиралей по окружностиСкачать

Рисование круговых (полярных) сеток

Нажмите и удерживайте инструмент «Отрезок линии» (). Выберите инструмент «Полярная сетка» .

Выполните одно из следующих действий:

Перетащите курсор, пока не получите сетку нужного размера.

Щелкните, чтобы задать неподвижную точку сетки. Чтобы определить точку, из которой будет нарисована сетка, щелкните в диалоговом окне квадратик на локаторе неподвижной точки . После этого задайте любые из следующих параметров и нажмите кнопку ОК .

Размер по умолчанию. Определяет ширину и высоту всей сетки.

Концентрические разделители. Определяет количество круговых концентрических разделителей в сетке. Значение «Асимметрично» позволяет распределять концентрические разделители неравномерно с увеличением их частоты в сторону внутренней или внешней части сетки.

Радиальные разделители. Определяет количество радиальных разделителей между центром и периферической частью сетки. Значение «Асимметрично» позволяет распределять радиальные разделители неравномерно с увеличением их частоты по часовой стрелке или против часовой стрелки.

Создать составной контур на основе эллипсов. Преобразует концентрические круги в отдельные составные контуры и добавляет в них заливку через один.

Окрашивать сетку в цвет заливки. Сетка окрашивается в текущий цвет заливки (в противном случае заливка не задается).

Видео:20/1.Adobe Illustrator. Инструменты - ПРЯМАЯ ЛИНИЯ, ДУГА, СПИРАЛЬ. Максимально подробно.Скачать

Как начертить правильную спираль

Спиралью называется плоская кривая, описываемая точкой, удаляющейся от центра при совершении кругового движения в плоскости чертежа вокруг центра спирали. На практике различают спирали с постоянным и постепенно возрастающим расстоянием между завитками. Обычно спирали строят по точкам и вычерчивают с помощью лекала.

Для того чтобы расчертить спираль, необходимо наметить не менее двух ее центров. Если вычерчивают спираль из трех или более центров, то обычно центрами спирали являются вершины правильного треугольника или правильного многоугольника. Каждую дугу проводят из последующей вершины до пересечения с лучом из угла треугольника или многоугольника. Радиус при этом каждый раз увеличивается на длину, равную длине стороны треугольника или многоугольника.

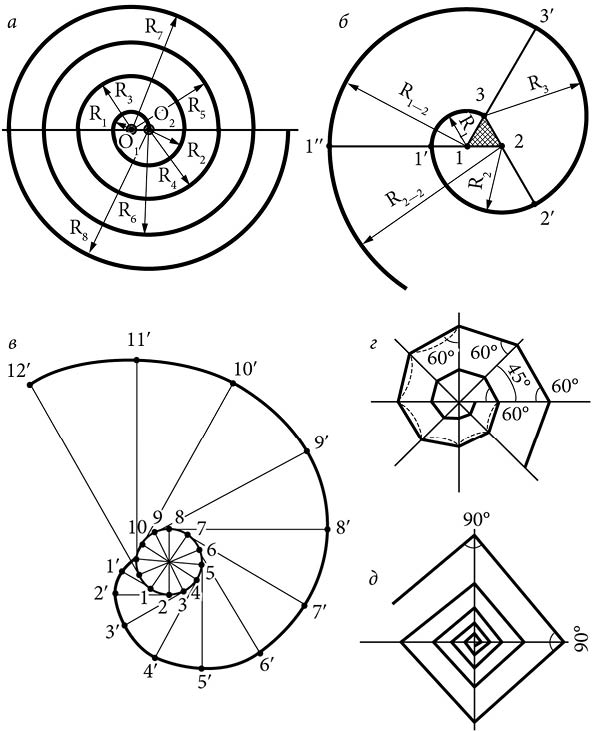
Рассмотрим, например, как начертить так называемую «архимедову спираль» (рис. 17, а ). Для этого нужно провести горизонтальную линию и отметить на ней две точки О 1 и О 2, отстоящие одна от другой примерно на 3 мм. Поставив ножку циркуля в одну из этих точек (О 1), проведите дугу радиусом 3 мм (R 1), равную половине окружности. Концы этой дуги должны опираться на горизонтальную ось (в данном примере – сверху).

Затем перенесите ножку циркуля во вторую из отмеченных точек и увеличьте его раствор так, чтобы карандаш попал в конец первой дуги. Снова проведите половину окружности радиусом R 2, опирающуюся на горизонтальную линию, но уже с противоположной стороны (снизу). Таким же образом, переставляя ножку циркуля то в первую, то во вторую точку и каждый раз увеличивая его раствор, продолжайте разворачивать спираль. На рис. 17, а , изображено четыре полных оборота.

Для построения спирали, имеющей три центра (рис. 17, б), находящихся на равных расстояниях один от другого, необходимо предварительно построить равносторонний треугольник 1–2–3 (заштрихован) и продолжить его стороны так, как это показано на рисунке (линии 1–1’, 2–2’ и 3–3’ ).

Из центра 1 проводим дугу 3–1’ радиусом R 1, равным длине стороны треугольника, до пересечения с продолжением стороны 1–1’ . Затем из центра 2 описываем дугу радиусом R 2 = 2R 1 до пересечения с продолжением стороны 2 (линия 2–2’ ). После этого из центра 3 проводим дугу радиусом R 3 = 3R 1 до пересечения с продолжением стороны 3 (линия 3–3’ ) в точке 3’ . После этого возвращаемся в центр 1 и продолжаем построение в такой же последовательности, каждый раз увеличивая радиус дуги на величину стороны треугольника.

Рис. 17. Построение спиралей: а – «архимедова спираль» с двумя центрами; б – трехцентровая спираль; в – эвольвента круга; г, д – ломаные (хордовые) спирали.

Аналогично выполняют спирали с четырьмя, пятью и т. д. центрами.

Эвольвента круга (рис. 17, в ) – это плоская кривая, образуемая точкой на прямой, которая перемещается без скольжения по неподвижной окружности заданного радиуса. Эта кривая иногда называется разверткой окружности. Построение эвольвенты начинается с деления заданной окружности на произвольное число равных частей, например 12. В каждой точке деления проводим касательные к окружности. На каждой из этих касательных последовательно откладываем длину окружности, равную πd /12: в точке 1 – πd /12, в точке 2 – 2πd /12, в точке 3 – 3πd /12 и т. д. На касательной к точке 12 откладываем длину окружности, равную πd . Соединяя последовательно плавной кривой по лекалу полученные на касательных точки 1’, 2’, 3’ и т. д., получим кривую, называемую эвольвентой.

Схема построения ломаных спиралей показана на рис. 17, г, д . Они строятся так же, как и циркульные, но дуги заменяются соответствующими хордами.

Золотая спираль или спираль Фибоначчи — логарифмическая спираль, коэффициент роста которой равен φ 4 , где φ — золотое сечение. Коэффициент роста логарифмической спирали показывает во сколько раз изменился полярный радиус спирали при повороте на угол 360°. [1] Свое название эта спираль получила из-за связи с последовательностью вложенных друг в друга прямоугольников с отношением сторон, равным φ , которые принято называть золотыми. Золотую спираль можно как вписать в систему таких прямоугольников, так и описать вокруг нее. Популярность золотая спираль приобрела из-за того, что известная с начала XVI века и применяющаяся в искусстве [2] спираль, построенная по методу Дюрера [3] [4] , оказалась хорошей аппроксимацией для золотой спирали (см. рисунок)

Видео:Уравнение окружности (1)Скачать

Содержание

Видео:Как начертить золотую спиральСкачать

Формула [ править | править код ]

Уравнение для золотой спирали в полярной системе координат то же самое, что и для других логарифмических спиралей, но со специальным значением коэффициента роста – φ 4 :

r = a φ ± 2 θ π >> ,

где a — произвольная положительная вещественная константа, а φ = 5 + 1 2 >+1> >> — золотое сечение.

Основное свойство логарифмической спирали: угол между радиус-вектором, исходящим из полюса, и касательной к спирали – μ – постоянен, и для золотой спирали определяется формулой:

tg ⁡ μ = r r ′ = π 2 ln ⁡ φ mu = , где r ′ =”” d r d θ >> .

Откуда μ ≈ 73 ∘ > .

Видео:СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]Скачать

Приближения золотой спирали [ править | править код ]

Существует несколько похожих спиралей, которые близки, но не совпадают в точности с золотой спиралью [5] , с которой их часто путают.

Как уже было написано выше, при вписывании золотой спирали в последовательность вложенных друг в друга золотых прямоугольников, она аппроксимируется спиралью, построенной по методу Дюрера. Золотой прямоугольник можно разделить на квадрат и подобный ему прямоугольник, его, в свою очередь, разделить тем же образом, и продолжать этот процесс произвольное число раз. Если в эти квадраты вписать соединенные между собой четвертинки окружностей, то получается спираль, изображенная на первом рисунке.

Ещё одной аппроксимацией является спираль Фибоначчи, которая строится подобно вышеописанной спирали, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины. Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов (см. второй рисунок).

Видео:Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Спирали в природе [ править | править код ]

В природе встречаются приближения к логарифмическим спиралям с коэффициентом роста равным φ k . Так раковины моллюсков Nautilus pompilius и окаменелых аммонитов хорошо описываются при k = 2, а раковины некоторых улиток при k = 1. [6] Отношение длин трех витков спирали уха у человека равно φ [7] , что соответствует спирали с k = 1. Рукава спиральных галактик, несмотря на существующие утверждения [8] , если и описываются логарифмической, то не золотой спиралью. В данном случае, описание ею является проявлением случайной близости. Недавний анализ спиралей, встречающихся в роговичном эпителии мышей, показал, что там встречаются как золотая, так и другие логарифмические спирали. [9]

Построение спирали Архимеда.

Спираль Архимеда – это траектория точки, движущейся с постоянной скоростью от центра окружности по

радиусу, вращающемуся также с постоянной угловой скоростью.

1. Делим радиус окружности на одинаковое число равных частей (в примере на 8).

2. Делим окружность на такое же число равных частей.

3. Проводим лучи из центра через точки деления окружности.

4. На первом луче откладываем одно деление радиуса.

5. На втором луче откладываем два деления радиуса и т. д.

6. Если строить спираль дальше, то на луче 1 откладываем 8+1 деление радиуса (получаем точку IX ).

7. На втором луче откладываем 8+2 деления радиуса (получаем точку X) .

8. На третьем луче откладываем 8+3 деления радиуса (получаем точку XI) и т. д.

Соединяем точки по лекалу.

Спираль. Спираль Архимеда. Построение спирали Архимеда.

📺 Видео

Числовая спираль в ГеогебреСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Окружность Эйлера (окружность 9 точек) и прямая ЭйлераСкачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

9 класс, 7 урок, Уравнение прямойСкачать

8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Логарифмическая спиральСкачать