Сообщение о параллельных и перпендикулярных прямых с чертежом (4 видео)

Сообщение о параллельных и перпендикулярных прямых с чертежом

Определение.1. Параллельные прямое
Определение.2. Перпендикулярные прямые
Теорема.1. I свойство параллельных прямых
Теорема.2. II свойство параллельных прямых
Теорема.3. III свойство параллельных прямых
Теорема.4. IV свойство параллельных прямых
Теорема.5. V свойство параллельных прямых
Теорема.6. I признак параллельных прямых
Теорема.7. II признак параллельных прямых
Теорема.8. III признак параллельных прямых
Теорема.9. IV признак параллельных прямых
Теорема 10. V признак параллельных прямых
Теорема 11. Две прямые, параллельные третей
Теорема 11.1 Следствие
Теорема 12. Прямая, пересекающая одну из параллельных прямых
Теорема 13. Отрезки параллельных прямых
Теорема 14. Теорема Фалеса
Теорема 14.1. Параллельные прямые, пересекающие стороны угла
Теорема 15. Прямая, перпендикулярна одной из параллельных прямых
Теорема 16. Две (и более) прямые, перпендикулярные третей прямой

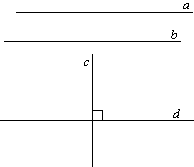
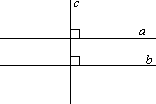
Определение 1. Параллельными называются прямые, которые не пересекаются, сколько бы мы их не продолжали.
На рисунке a и b.

Определение 2. Перпендикулярными называются прямые, которые пересекаются под прямым углом.
На рисунке c и d.
При пересечении пары прямых (параллельных в данном случае) некой прямой (такая прямая называется секущей прямой) образуются (акромя пройденных нами в теме углы смежных и вертикальных) следующие углы:
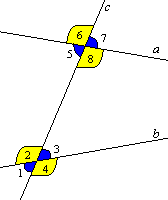
Внутренние накрестлежащие углы — 2 и 8; 3 и 5
Внешние накрестлежащие углы — 1 и 7; 4 и 6
Внутренние односторонние углы — 2 и 5; 3 и 8
Внешние односторонние углы — 1 и 6; 4 и 7
Соответственные углы — 1 и 5; 2 и 6; 3 и 7; 4 и 8
Между этими углами можно вывести закономерности. Свойства параллельных прямых:
Теорема 1. Внутренние накрестлежащие углы равны

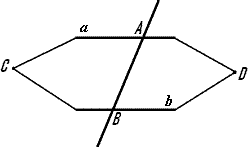
Доказательство: Пусть a и b — две параллельные прямые, c — секущая, A и B — точки пересечения секущей с этими прямыми. Пусть утверждение теоремы ложно. Проведем тогда через точку A прямую d, такую что внутренние накрест лежащие углы при прямых b и d и секущей c равны. Тогда по первому признаку параллельности прямых, прямые b и d параллельны. Но прямые b и a параллельны. Значит, через точку A проходят две прямые — a и d, параллельные прямой b. Это противоречит IX аксиоме. Значит, утверждение теоремы верно. Теорема доказана.
Теорема 2. Внешние накрестлежащие углы равны

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 3. Сумма внутренних односторонних углов равна 180 градусам

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 4. Сумма внешних односторонних углов равна 180 градусам

Доказательство: Очевидно из первого свойства параллельных прямых.
Теорема 5. Соответственные углы равны

Доказательство: Очевидно из первого свойства параллельных прямых.

Теорема 6. Если при пересечении двух прямых а и b третей прямой с внутренние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Пусть прямые a и b пересекаются секущей в точках A и B, но прямые a и b пересекаются в точке C (рис. 15). Секущая c разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник ABD, равный треугольнику ABC, с вершиной D в другой полуплоскости. Угол DAB равен углу ABC, а значит, точка D лежит на прямой a по условию. Аналогично точка D лежит на прямой b. Следовательно, точка D принадлежит прямым a и b. Значит, прямые a и b пересекаются в двух точках — C и D. Противоречие. Значит, исходное предположение не верно. Теорема доказана.
Теорема 7. Если при пересечении двух прямых а и b третей прямой с внешние накрестлежащие углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 8. Если при пересечении двух прямых а и b третей прямой с сумма внутренних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 9. Если при пересечении двух прямых а и b третей прямой с сумма внешних односторонних углов равна 180 градусам (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 10. Если при пересечении двух прямых а и b третей прямой с соответственные углы равны (одна пара), то такие прямые а и b являются параллельными

Доказательство: Очевидно из первого признака параллельности прямых.
Теорема 11. Две прямые, параллельные третей, параллельны.

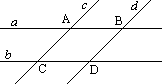
Доказательство: Пусть прямые a и b параллельны прямой c. Допустим, что прямые a и b не па-раллельны. Тогда либо прямые a и b совпадают, что противоречит условию, либо пересекаются в не-которой точке S. Тогда через точку S проходит две прямые — a и b, параллельные прямой c, что противоречит IX аксиоме. Значит, исходное предположение не верно. Теорема доказана.
Теорема 11.1. Если параллельно одной из двух параллельных прямых провести третью прямую, вторая из этих прямых либо параллельна третьей, либо совпадает с ней.

Доказательство: Очевидно из теоремы 11 параллельности прямых.
Теорема 12. Если прямая пересекает одну из параллельных прямых, то она пересекает и вторую.
Теорема 13. Отрезки параллельных прямых, заключенные между некой (иной) парой параллельных прямых, равны.
Теорема 14. (Теорема Фалеса) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

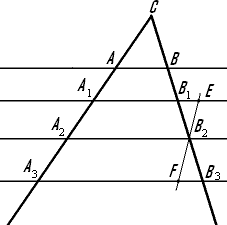
Доказательство: Пусть A₁, A₂, A₃ — точки пересечения параллельных прямых с одной из сторон угла, и точка A₂ лежит между точками A₁ и A₃. Пусть B₁, B₂, B₃ — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A₁A₂ = A₂A₃, то B₁B₂ = B₂B₃. Проведем через точку B₂ прямую EF, параллельную прямой A₁A₃. Треугольники EB₂B₁ и FB₂B₃ равны по второму признаку равенства треугольников. У них стороны EB₂ и FA₂ равны по условию, углы B₁B₂E и B₃B₂F равны как вертикальные, а углы B₁EB₂ и B₂FB₃ равны как внутренние накрест лежащие при секущей EF. Значит, B₁B₂ = B₂B₃. Что и требовалось доказать.
Теорема 14.1.. Параллельные прямые, пересекая стороны угла, отсекают пропорциональные отрезки.

Теорема 15. Две (и более) прямые, перпендикулярные третей прямой, параллельны.

Доказательство: Действительно, внутренние накрест лежащие углы равны 90°. Следовательно, по первому признаку параллельных прямых, эти прямые параллельны.
Теорема 16. Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй.

Доказательство: Очевидно из теоремы 15.

Содержание

Прямая. Параллельные и перпендикулярные прямые.
теория по математике 📈 планиметрия
Обозначения прямой
Признаки параллельности прямых
Аксиома параллельных прямых
Следствия из аксиом параллельных прямых
Перпендикулярные прямые
Перпендикулярные и параллельные прямые
Перпендикулярные прямые
Готовые работы на аналогичную тему
Параллельные прямые
🔍 Видео

Видео:Перпендикулярные прямыеСкачать

Прямая. Параллельные и перпендикулярные прямые.

теория по математике 📈 планиметрия

Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

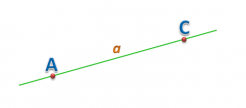
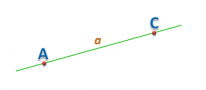
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

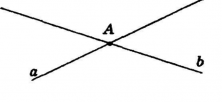
Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых

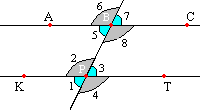
Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.

Необходимо запомнить названия следующих углов:

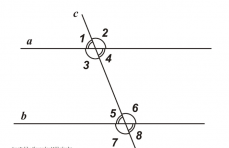
накрест лежащие углы: 4 и 5; 3 и 6;
односторонние углы: 4 и 6; 3 и 5;
соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 0 , то прямые параллельны.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Следствия из аксиом параллельных прямых

Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Видео:Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Перпендикулярные прямые

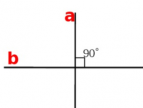
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.

Видео:Параллельные прямые. 6 класс.Скачать

Перпендикулярные и параллельные прямые

Вы будете перенаправлены на Автор24

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Перпендикулярные прямые

Перпендикулярными прямыми называются прямые, которые располагаются на одной плоскости и пересекаются под прямым углом.

Прямой угол равен $90^о$.

Перпендикулярными могут быть не только прямые, но и лучи, и отрезки.

Рассмотрим прямоугольник и квадрат. В них все углы прямые, т.е. равны 90о. Следовательно, соседние стороны каждой и этих геометрических фигур перпендикулярны между собой.

Для построения прямого угла, например, в школьной тетради, можно использовать чертежный треугольник, у которого один из углов равен $90^circ$. Также можно воспользоваться транспортиром: провести ровную линию, отметить точку возле цифры $90$ и построить проекцию из этой точки на проведенную прямую. Самый простой способ – нарисовать перпендикулярные прямые по клеточкам в тетради, т.к. они имеют форму квадрата со сторонами, которые располагаются под прямым углом.

Прямые, которые пересекаются под прямым углом, называются перпендикулярными прямыми.

Перпендикулярные прямые сокращенно в математике обозначают с помощью специального знака «perp». Например, тот факт, что прямая $AB$ перпендикулярна относительно прямой $MN$ записывается как $AB perp MN$.

Если $AB perp MN$, то $MN perp AB$.

Отрезки (или лучи), которые лежат на перпендикулярных прямых, называются перпендикулярными отрезками (или лучами).

Готовые работы на аналогичную тему

Видео:Параллельные и перпендикулярные прямые.Скачать

Параллельные прямые

Представим плоскость, на которой проведена одна прямая линия. Назовем ее $AB$. На этой же плоскости вне прямой отмечена точка $C$. Через эту точку $C$ можно провести бесконечное количество прямых, но только одна из них (назовем ее $CD$) никогда не пересечется с прямой $AB$. Говорят, что прямая $AB$ параллельна относительно прямой $CD.$

Параллельными прямыми называются две прямые, которые расположены на плоскости и не пересекаются.

Сформулируем еще и правило:

Через точку, которая не принадлежит на прямой, можно провести только одну прямую, которая будет параллельна исходной.

В жизни параллельные прямые можно встретить, например, на прямых участках железнодорожных путей или прямых участках трамвайных путей.

Довольно часто параллельные прямые встречаются в геометрических фигурах. Например, противоположные стороны квадрата, прямоугольника, параллелограмма, основания трапеции.

Такие геометрические фигуры, как квадрат и прямоугольник, интересны тем, что они содержат и перпендикулярные, и параллельные стороны.

Таким образом, две любые прямые на плоскости могут или пересекаться в одной точке, или не пересекаться.

Параллельные прямые сокращенно в математике обозначают с помощью специального знака «parallel». Например, тот факт, что прямая $AB$ параллельна прямой $MN$ записывается как $AB parallel MN$.

Если $AB parallel MN$, то $MN parallel AB$.

Отрезки (или лучи), которые лежат на параллельных прямых, называются параллельными отрезками (или лучами).

Рассмотрим квадрат $ABCD$.

Его стороны $AB$ и $CD$, $BC$ и $DA$ – попарно параллельные.

Стороны $AB$ и $BC$, $BC$ и $CD$, $CD$ и $DA$, $DA$ и $AB$ – попарно перпендикулярные.

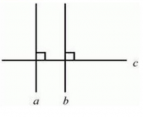
Если представить любые две прямые, которые находятся в одной плоскости, такие, что они перпендикулярны третей прямой, следовательно, эти прямые параллельные между собой.

Прямые $m$ и $n$ на рисунке перпендикулярны прямой $l$. Они параллельны друг другу.

В прямоугольнике противоположные стороны параллельны и образуют прямые углы с другими сторонами этого прямоугольника.

Для построения параллельных прямых можно использовать треугольник и линейку. На рисунке показано, как с помощью чертежных приборов можно начертить прямую $n$, которая проходит через точку $A$ параллельно прямой $m$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 20 06 2021