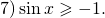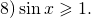Sin x больше 0 на окружности (2 видео) | Курс школьной геометрии

sin(x)>0 (неравенство)

Содержание

Шаг 1. Введите неравенство
Решение
Где учитесь?
Здравствуй, уважаемый посетитель!
Узнать ещё
a»>sinx>a
🌟 Видео

Видео:Решить тригонометрические неравенства sinxСкачать

Шаг 1. Введите неравенство

Укажите решение неравенства: sin(x)>0 (множество решений неравенства)

Решение

Дано неравенство:
$$sin > 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$sin = 0$$
Решаем:
Дано уравнение
$$sin = 0$$
— это простейшее тригонометрическое ур-ние

Получим:
$$sin = 0$$
Это ур-ние преобразуется в
$$x = 2 pi n + operatorname$$
$$x = 2 pi n — operatorname + pi$$
Или
$$x = 2 pi n$$
$$x = 2 pi n + pi$$
, где n — любое целое число
$$x_ = 2 pi n$$
$$x_ = 2 pi n + pi$$
$$x_ = 2 pi n$$
$$x_ = 2 pi n + pi$$
Данные корни
$$x_ = 2 pi n$$
$$x_ = 2 pi n + pi$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_ 0$$
$$sin<left (2 pi n — frac right )> > 0$$

Тогда
$$x 2 pi n wedge x

Видео:Как решать тригонометрические неравенства?Скачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Здравствуй, уважаемый посетитель!

Меня зовут Александр Бабаев. И это мой сайт.Он посвящён не только математике. Вы найдёте здесь много интересных и полезных, я надеюсь, для себя вещей.
Кроме того, что здесь выкладываются интересные задачки, разбираются непонятные моменты и осуществляется помощь в решении трудных задач, на сайте выкладывается фото и видео мероприятий, которые я провожу, в блоге вы найдёте обсуждение различных проблем с которыми я сталкиваюсь и могу поделиться с вами, дорогой посетитель.
Для моих замечательных студентов есть специальный раздел, где они могут посмотреть всё, что им нужно для овладевания курсом математики.
Более того, в специальных разделах я публикую мои рецензии на просмотренные мной фильмы и игры.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Что больше ➜ sin4 или sin5 ➜ Супер способСкачать

a»>sinx>a

Простейшие тригонометрические неравенства вида sin x>a — основа для решения более сложных тригонометрических неравенств.

Рассмотрим решение простейших тригонометрических неравенств вида sin x>a на единичной окружности.

С помощью ассоциации косинус-колобок (оба начинаются с ко-, оба «кругленькие»), вспоминаем, что косинус — это x, соответственно, синус — y. Отсюда строим график y=a — прямую, параллельную оси ox. Если неравенство строгое, точки пересечения единичной окружности и прямой y=a выколотые, если неравенство нестрогое — точки закрашиваем (как легко запомнить, когда точка выколотая, когда — закрашенная, смотрите здесь ). Наибольшие затруднение при решении простейших тригонометрических неравенств вызывает правильное нахождение точек пересечения единичной окружности и прямой y=a.

Первую из точек найти несложно — это arcsin a. Определяем путь, по которому из первой точки идем ко второй. На прямой y=a sinx=a, сверху, над прямой, sin x>a, а ниже, под прямой, sin xa, нам нужен верхний путь. Таким образом, от первой точки, arcsin a, ко второй, мы идем против часовой стрелки, то есть в сторону увеличения угла. Мы не доходим до п. На сколько не доходим? На arcsin a. Раз не дошли до п, то вторая точка меньше п, значит, чтобы ее найти, надо из п вычесть arcsina. Решением неравенства sin x>a в этом случае является промежуток от arcsin a до п-arcsin a. Поскольку период синуса равен 2п, чтобы учесть все решения неравенства (а таких промежутков — бесконечное множество), к каждому из концов интервала прибавляем 2пn, где n — целое число (n принадлежит Z).

2) a=0, то есть sin x>0

В этом случае первая точка промежутка — 0, вторая — п. К обоим концам промежутка с учетом периода синуса прибавляем 2пn.

3) при a=-1, то есть sinx>-1

В этом случае первая точка -п/2, а чтобы попасть во вторую, обходим всю окружность против часовой стрелки. Попадаем в точку -п/2+2п=3п/2. Чтобы учесть все интервалы, являющиеся решением данного неравенства, к обоим концам прибавляем 2пn.

4) sinx>-a, при 0

Первая точка — как обычно, arcsin(-a)=-arcsina. Чтобы попасть во вторую точку, идем верхним путем, то есть в сторону увеличения угла.

На этот раз мы за п переходим. На сколько переходим? На arcsin x. Значит, вторая точка — это п+arcsin x. Почему нет минуса? Потому что минус в записи -arcsin a обозначает движение по часовой стрелки, а мы шли против. И в заключении, к каждому концу интервала прибавляем 2пn.

5) sinx>a, если а>1.

Единичная окружность лежит целиком под прямой y=a. Нет ни одной точки выше прямой. Значит, решений нет.

6) sinx>-a, где a>1.

В этом случае вся единичная окружность целиком лежит над прямой y=a. Поэтому любая точка удовлетворяет условию sinx>a. Значит, x — любое число.

И здесь x — любое число, поскольку точки -п/2+2пn входят в решение, в отличие от строгого неравенства sinx>-1. Ничего исключать не надо.

Единственной точкой на окружности, удовлетворяющей данному условию, является п/2. С учетом периода синуса, решением данного неравенства является множество точек x=п/2+2пn.

Например, решить неравенство sinx>-1/2: