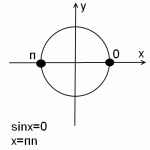Син равен 0 на окружности

Знание — сила. Познавательная информация

sinx=0

Эта ассоциация позволяет легко запомнить, где синус равен 0, и быстро решить уравнение sin x=0.

Как обычно, частные случаи синуса рассматриваем на единичной окружности.

Используем ассоциацию косинус-колобок. Оба начинаются с ко-, в названии cos x буква o тоже косвенно на колобка указывает. Колобок движется по горизонтали. На координатной плоскости движение по горизонтали происходит вдоль оси x.

Поэтому cos x — это x, соответственно, sin x — это y.

Таким образом, чтобы найти, где синус равен 0, нужно выяснить, в каких точках y=0.

Раз y=0, то движения вверх-вниз не происходит.

На единичной окружности условию sin x=0 удовлетворяют две точки: 0 и π.

Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть π.

Поскольку таких точек, в которых синус равен 0, бесконечное множество, прибавляем не π, а πn, где n — целое число (то есть n принадлежит Z): x=0+πn.

Следовательно, решение уравнения sin x=0, есть множество точек

Таблица СИНУСОВ для углов от 0° до 360° градусов

СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.

Малая таблица значений тригонометрических функций (в радианах и градусах)

α (радианы)	0	π/6	π/4	π/3	π/2	π	√3π/2	2π
α (градусы)	0°	30°	45°	60°	90°	180°	270°	360°
SIN α (СИНУС)	0	1/2	√ 2/2	√3 /2	1	0	-1	0

Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°

Угол в градусах	Sin (Синус)
0°	0
1°	0.0175
2°	0.0349
3°	0.0523
4°	0.0698
5°	0.0872
6°	0.1045
7°	0.1219
8°	0.1392
9°	0.1564
10°	0.1736
11°	0.1908
12°	0.2079
13°	0.225
14°	0.2419
15°	0.2588
16°	0.2756
17°	0.2924
18°	0.309
19°	0.3256
20°	0.342
21°	0.3584
22°	0.3746
23°	0.3907
24°	0.4067
25°	0.4226
26°	0.4384
27°	0.454
28°	0.4695
29°	0.4848
30°	0.5
31°	0.515
32°	0.5299
33°	0.5446
34°	0.5592
35°	0.5736
36°	0.5878
37°	0.6018
38°	0.6157
39°	0.6293
40°	0.6428
41°	0.6561
42°	0.6691
43°	0.682
44°	0.6947
45°	0.7071
46°	0.7193
47°	0.7314
48°	0.7431
49°	0.7547
50°	0.766
51°	0.7771
52°	0.788
53°	0.7986
54°	0.809
55°	0.8192
56°	0.829
57°	0.8387
58°	0.848
59°	0.8572
60°	0.866
61°	0.8746
62°	0.8829
63°	0.891
64°	0.8988
65°	0.9063
66°	0.9135
67°	0.9205
68°	0.9272
69°	0.9336
70°	0.9397
71°	0.9455
72°	0.9511
73°	0.9563
74°	0.9613
75°	0.9659
76°	0.9703
77°	0.9744
78°	0.9781
79°	0.9816
80°	0.9848
81°	0.9877
82°	0.9903
83°	0.9925
84°	0.9945
85°	0.9962
86°	0.9976
87°	0.9986
88°	0.9994
89°	0.9998
90°	1

Полная таблица синусов для углов от 91° до 180°

Угол в градусах	Sin (Синус)
91°	0.9998
92°	0.9994
93°	0.9986
94°	0.9976
95°	0.9962
96°	0.9945
97°	0.9925
98°	0.9903
99°	0.9877
100°	0.9848
101°	0.9816
102°	0.9781
103°	0.9744
104°	0.9703
105°	0.9659
106°	0.9613
107°	0.9563
108°	0.9511
109°	0.9455
110°	0.9397
111°	0.9336
112°	0.9272
113°	0.9205
114°	0.9135
115°	0.9063
116°	0.8988
117°	0.891
118°	0.8829
119°	0.8746
120°	0.866
121°	0.8572
122°	0.848
123°	0.8387
124°	0.829
125°	0.8192
126°	0.809
127°	0.7986
128°	0.788
129°	0.7771
130°	0.766
131°	0.7547
132°	0.7431
133°	0.7314
134°	0.7193
135°	0.7071
136°	0.6947
137°	0.682
138°	0.6691
139°	0.6561
140°	0.6428
141°	0.6293
142°	0.6157
143°	0.6018
144°	0.5878
145°	0.5736
146°	0.5592
147°	0.5446
148°	0.5299
149°	0.515
150°	0.5
151°	0.4848
152°	0.4695
153°	0.454
154°	0.4384
155°	0.4226
156°	0.4067
157°	0.3907
158°	0.3746
159°	0.3584
160°	0.342
161°	0.3256
162°	0.309
163°	0.2924
164°	0.2756
165°	0.2588
166°	0.2419
167°	0.225
168°	0.2079
169°	0.1908
170°	0.1736
171°	0.1564
172°	0.1392
173°	0.1219
174°	0.1045
175°	0.0872
176°	0.0698
177°	0.0523
178°	0.0349
179°	0.0175
180°	0

Таблица синусов для углов 181° — 270°

Угол	Sin (Синус)
181°	-0.0175
182°	-0.0349
183°	-0.0523
184°	-0.0698
185°	-0.0872
186°	-0.1045
187°	-0.1219
188°	-0.1392
189°	-0.1564
190°	-0.1736
191°	-0.1908
192°	-0.2079
193°	-0.225
194°	-0.2419
195°	-0.2588
196°	-0.2756
197°	-0.2924
198°	-0.309
199°	-0.3256
200°	-0.342
201°	-0.3584
202°	-0.3746
203°	-0.3907
204°	-0.4067
205°	-0.4226
206°	-0.4384
207°	-0.454
208°	-0.4695
209°	-0.4848
210°	-0.5
211°	-0.515
212°	-0.5299
213°	-0.5446
214°	-0.5592
215°	-0.5736
216°	-0.5878
217°	-0.6018
218°	-0.6157
219°	-0.6293
220°	-0.6428
221°	-0.6561
222°	-0.6691
223°	-0.682
224°	-0.6947
225°	-0.7071
226°	-0.7193
227°	-0.7314
228°	-0.7431
229°	-0.7547
230°	-0.766
231°	-0.7771
232°	-0.788
233°	-0.7986
234°	-0.809
235°	-0.8192
236°	-0.829
237°	-0.8387
238°	-0.848
239°	-0.8572
240°	-0.866
241°	-0.8746
242°	-0.8829
243°	-0.891
244°	-0.8988
245°	-0.9063
246°	-0.9135
247°	-0.9205
248°	-0.9272
249°	-0.9336
250°	-0.9397
251°	-0.9455
252°	-0.9511
253°	-0.9563
254°	-0.9613
255°	-0.9659
256°	-0.9703
257°	-0.9744
258°	-0.9781
259°	-0.9816
260°	-0.9848
261°	-0.9877
262°	-0.9903
263°	-0.9925
264°	-0.9945
265°	-0.9962
266°	-0.9976
267°	-0.9986
268°	-0.9994
269°	-0.9998
270°	-1

Таблица синусов для углов от 271° до 360°

Угол	Sin (Синус)
271°	-0.9998
272°	-0.9994
273°	-0.9986
274°	-0.9976
275°	-0.9962
276°	-0.9945
277°	-0.9925
278°	-0.9903
279°	-0.9877
280°	-0.9848
281°	-0.9816
282°	-0.9781
283°	-0.9744
284°	-0.9703
285°	-0.9659
286°	-0.9613
287°	-0.9563
288°	-0.9511
289°	-0.9455
290°	-0.9397
291°	-0.9336
292°	-0.9272
293°	-0.9205
294°	-0.9135
295°	-0.9063
296°	-0.8988
297°	-0.891
298°	-0.8829
299°	-0.8746
300°	-0.866
301°	-0.8572
302°	-0.848
303°	-0.8387
304°	-0.829
305°	-0.8192
306°	-0.809
307°	-0.7986
308°	-0.788
309°	-0.7771
310°	-0.766
311°	-0.7547
312°	-0.7431
313°	-0.7314
314°	-0.7193
315°	-0.7071
316°	-0.6947
317°	-0.682
318°	-0.6691
319°	-0.6561
320°	-0.6428
321°	-0.6293
322°	-0.6157
323°	-0.6018
324°	-0.5878
325°	-0.5736
326°	-0.5592
327°	-0.5446
328°	-0.5299
329°	-0.515
330°	-0.5
331°	-0.4848
332°	-0.4695
333°	-0.454
334°	-0.4384
335°	-0.4226
336°	-0.4067
337°	-0.3907
338°	-0.3746
339°	-0.3584
340°	-0.342
341°	-0.3256
342°	-0.309
343°	-0.2924
344°	-0.2756
345°	-0.2588
346°	-0.2419
347°	-0.225
348°	-0.2079
349°	-0.1908
350°	-0.1736
351°	-0.1564
352°	-0.1392
353°	-0.1219
354°	-0.1045
355°	-0.0872
356°	-0.0698
357°	-0.0523
358°	-0.0349
359°	-0.0175
360°	0

Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.

Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».

Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.

Чему равен синус 45? …

— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071

Синус

Синус – одна из тригонометрических функций. Значение синуса определяется для угла или для числа (в этом случае используют числовую окружность).

Аргумент и значение

Синус острого угла

Синус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению противолежащего катета к гипотенузе.

1) Пусть дан угол и нужно определить синус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить (sinA).

Синус числа

Синус числа можно определить с помощью числовой окружности – синус числа равен ординате соответствующей точки на ней.

Числовая окружность позволяет определить синус любого числа, но обычно находят синус чисел как-то связанных с Пи : (frac) , (frac) , (-2π).

Например, для числа (frac) — синус будет равен (0,5). А для числа (-) (frac) он будет равен (-) (frac<sqrt>) (приблизительно (-0,71)).

Подробнее как вычисляется синус разных чисел можно прочитать в этой статье .

Значение синуса всегда лежит в пределах от (-1) до (1). При этом вычислен он может быть для абсолютно любого угла и числа.

Синус любого угла

Благодаря единичному кругу можно определять тригонометрические функции не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать — проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить (sin∠КОА) с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам (sin⁡∠KOA).

Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) — целых семь.

Как вы могли заменить, и синус числа, и синус произвольного угла определяется практически одинаково. Изменяются только способ нахождения точки на окружности.

Связь с другими тригонометрическими функциями:

— косинусом того же угла (или числа): основным тригонометрическим тождеством (sin^2⁡x+cos^2⁡x=1)
— тангенсом и косинусом того же угла (или числа): формулой (tg⁡x=) (frac)
— котангенсом того же угла (или числа): формулой (1+сtg^2⁡x=) (frac)
Другие наиболее часто применяемые формулы смотри здесь .

Функция (y=sin⁡x)

Если отложить по оси (x) углы в радианах, а по оси (y) — соответствующие этим углам значения синуса, мы получим следующий график:

График данной функции называется синусоида и обладает следующими свойствами:

— область определения – любое значение икса: (D(sin⁡x )=R)
— область значений – от (-1) до (1) включительно: (E(sin⁡x )=[-1;1])
— нечетная: (sin⁡(-x)=-sin⁡x)
— периодическая с периодом (2π): (sin⁡(x+2π)=sin⁡x)
— точки пересечения с осями координат:
ось абсцисс: ((πn;0)), где (n ϵ Z)
ось ординат: ((0;0))
— промежутки знакопостоянства:
функция положительна на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
— промежутки возрастания и убывания:
функция возрастает на интервалах: ((-) (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
функция убывает на интервалах: (() (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
— максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=) (frac) (+2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=-) (frac) (+2πn), где (n ϵ Z).

🔥 Видео