Шестиугольник вписанный в окружность в диметрии (4 видео)

Шестиугольник вписанный в окружность в диметрии

Контрольные задания по теме: эпюр № 6

Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.

Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:

— изометрические, когда все три коэффициента искажения одинаковы (k_x=k_y=k_z);

— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (k_x= k_z ≠k_y);

— триметрические, когда все три коэффициенты искажения не равны между собой (k_x≠k_y≠k_z).

В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в 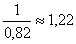раза.

Изометрические оси изображены на рисунке 57.

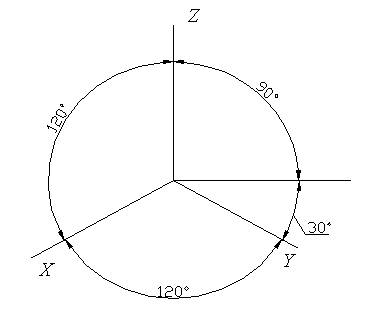
Рисунок 57

Построение изометрических осей можно выполнить при помощи циркуля (рисунок 58). Для этого сначала проводят горизонтальную линию и перпендикулярно к ней проводят ось Z. Из точки пересечения оси Z с горизонтальной линией (точка О) проводят вспомогательную окружность произвольным радиусом, которая пересекает ось Z в точке А. Из точки А этим же радиусом проводят вторую окружность до пересечения с первой в точках В и С. Полученную точку В соединяют с точкой О — получают направление оси Х. Таким же образом соединяют точку С с точкой О — получают направление оси Y.

Рисунок 58

Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.

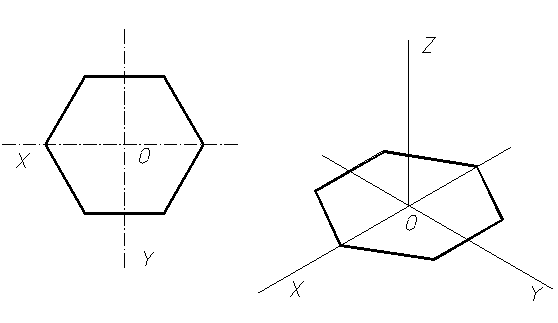
Рисунок 59

Построение окружности в прямоугольной изометрической проекции

Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.

Размер большой оси эллипса 1,22d, малой 0,7d, где d — диаметр той окружности, изометрия которой строится. На рисунке 60 показан графический способ определения большой и малой осей изометрического эллипса. Для определения малой оси эллипса соединяют точки С и D. Из точек С и D, как из центров, проводят дуги радиусов, равных СD, до взаимного их пересечения. Отрезок АВ — большая ось эллипса.

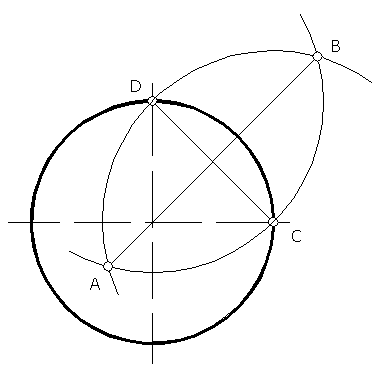
Рисунок 60

Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О₁, О₂, О₃, О₄, являющиеся центрами дуг овала (рисунок 61).

Для определения точек сопряжения проводят линии центров, соединяя О₁, О₂, О₃, О₄. из полученных центров О₁, О₂, О₃, О₄ проводят дуги радиусами R и R₁. размеры радиусов видны на чертеже.

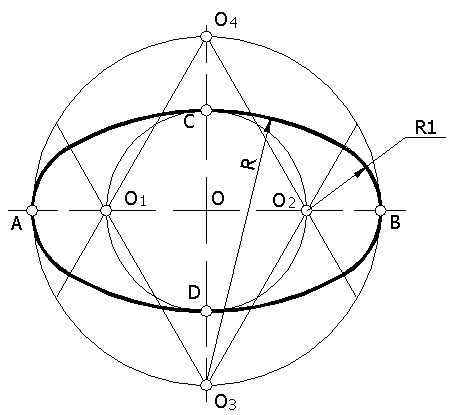
Рисунок 61

Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).

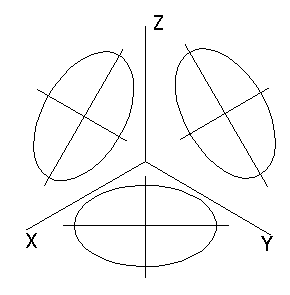
Рисунок 62

Штриховка и изометрической проекции

Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.

Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.

По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты k_x=k_z=1, k_y=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.

Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:

На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.

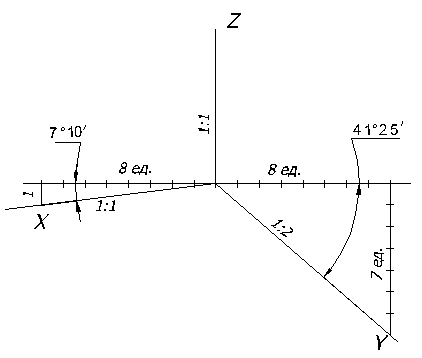
Рисунок 63

Построение диметрической проекции шестиугольника

Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П₁ (рисунок 64).

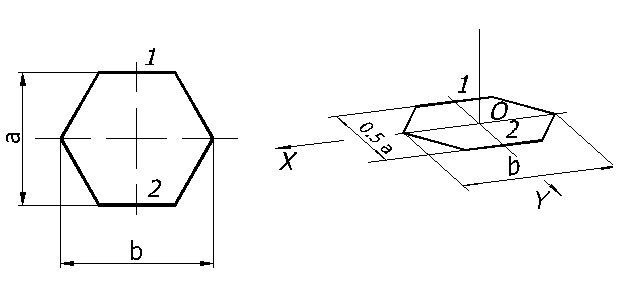
Рисунок 64

На оси Х откладываем отрезок равный величине b, чтобы его середина находилась в точке О, а по оси Y – отрезок а, размер которого уменьшен вдвое. Через полученные точки 1 и 2 проводим прямые параллельно оси ОХ, на которых откладываем отрезки равные стороне шестиугольника в натуральную величину с серединой в точках 1 и 2. Полученные вершины соединяем. На рисунке 65а изображен в диметрии шестиугольник, расположенный параллельно фронтальной плоскости, а на рисунке 66б -параллельно профильной плоскости проекции.

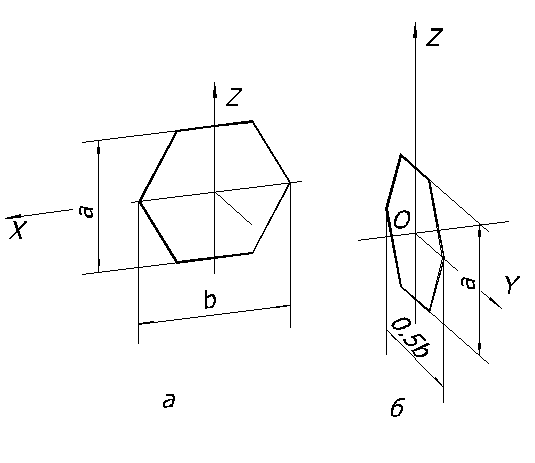
Рисунок 65

Построение окружности в диметрии

В прямоугольной диметрии все окружности изображаются эллипсами,

Длина большой оси для всех эллипсов одинакова и равна 1,06d. Величина малой оси различна: для фронтальной плоскости равна 0,95d , для горизонтальной и профильной плоскостей – 0,35 d.

На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).

Через точку О – начало аксонометрических осей, проводим две взаимно перпендикулярные прямые и откладываем на горизонтальной линии величину большой оси АВ=1,06d , а на вертикальной линии величину малой оси СD=0,35d. Вверх и вниз от О по вертикали откладываем отрезки ОО₁ и ОО₂, равные по величине 1,06d. Точки О₁ и О₂ являются центром больших дуг овала. Для определения еще двух центров (О₃ и О₄) откладываем на горизонтальной прямой от точек А и В отрезки АО₃ и ВО₄, равные ¼ величины малой оси эллипса, то есть d.

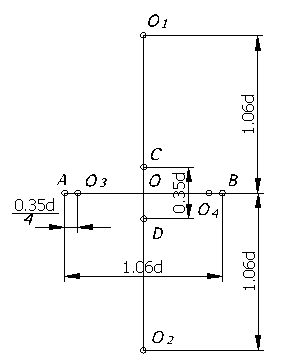
Рисунок 66

Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).

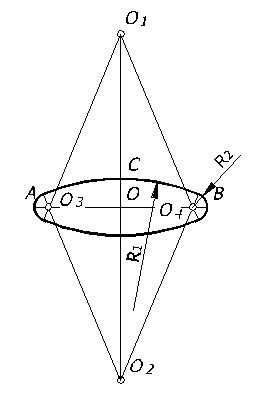
Рисунок 67

Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П₂, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О₁, О_2, О_3, О₄ – центры дуг овала (рисунок 68).

Из центров О₃ и О₄ описывают дугу радиусом R₂=О₃ М, а из центров О₁ и О₂ — дуги радиусом R₁= О₂ N

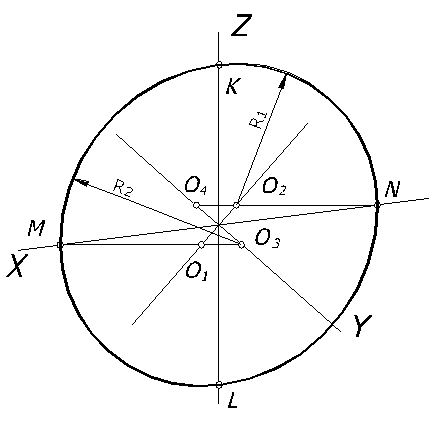
Рисунок 68

Штриховка а прямоугольной диметрии

Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).

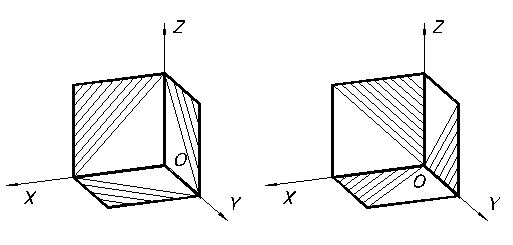
Рисунок 69

Какие виды аксонометрических проекций вы знаете?
Под каким углом расположены оси в изометрии?
Какую фигуру представляет изометрическая проекция окружности?
Как расположена большая ось эллипса для окружности, принадлежащей профильной плоскости проекций?
Какие приняты коэффициенты искажения по осям X, Y, Z для построения диметрической проекции?
Под какими углами расположены оси в диметрии?
Какой фигурой будет являться диметрическая проекция квадрата?
Как построить диметрическую проекцию окружности, расположенной во фронтальной проскости проекций?
Основные правила нанесения штриховки в аксонометрических проекциях.

Тема 12

Наверх

Заключение

Содержание

Консультации по отчетам к практике, контрольные, курсовые
Начертательная геометрия. Расчетно-графическая работа
Презентация по черчению на тему «Аксонометрия шестиугольника»
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Описание презентации по отдельным слайдам:
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Материал подходит для УМК
Дистанционные курсы для педагогов
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
🎦 Видео

Видео:Шестиугольник в изометрииСкачать

Консультации по отчетам к практике, контрольные, курсовые

Линейная алгебра

Смотреть онлайн бесплатно экстрасенс в новосибирске astrolog-novosibirsk.ru. Заходи на порнк!

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Начертательная геометрия. Расчетно-графическая работа

Построении в диметрической проекции плоских фигур.

Построим правильный шестиугольник в диметрической проекции.

В технической практике принято рассматривать образование поверхности (как и линии) с позиций кинематики – движения. Поверхность – это множество последовательных положений движущейся линии – образующей. Лекции по черчению, начертательной геометрии

По оси ox откладываются отрезки 01’ = 01 и 02’ = 02, а по оси oy – расстояние 03 и 04, уменьшенное в 2 раза /03’ и 04’/. Дальнейшие построения аналогичны построениям шестиугольника в изометрической проекции (рисунок 11.17).

Геометрические тела, имеющие квадратные поверхности, строятся преимущественно в прямоугольной диметрии (рис.11.12).

Построение окружности в диметрической проекции.

Окружности, лежащие в плоскостях, параллельных плоскостям проекции, проецируются на аксонометрическую плоскость проекций в эллипсы. Большая ось эллипсов равна 1,06 диаметра окружности, а малая ось эллипса – 0,35 Ø или 0,95 Ø.

Рассмотрим построение в прямоугольной диметрии окружности (рисунок 11.18).

В плоскости xoy через центр С1 проводим прямые, параллельные осям ox и oy и откладываем 1121 = 12,3’4’ = .

Направление большой оси эллипса перпендикулярно оси OZ и равно 1,06 Ø, малая ось перпендикулярна большой и равна 0,35 Ø. Аналогично строиться эллипс в плоскости YOZ. Во фронтальной плоскости XOZ большая ось эллипса перпендикулярна оси OY и равна 1,03 Ø, малая ось равна 0,95 Ø. По прямым параллельным осям OX и OZ, откладываю размер диаметра Ø (1222.3242), полученные точки соединяют плавной кривой.

Для упрощения построения эллипсы заменяют овалами. Построение овалов осуществляется различными способами. На рисунке 11.19 дано построение эллипсов по большой и малой осям. Построение понятно из чертежа.

Более удобен другой способ, при котором не требуется определение большой и малой осей эллипса (рисунок 11.20).

Разрез в аксонометрических проекциях.

При выполнении аксонометрических изображений сложных деталей, имеющие внутренние полости, применяют разрезы для выявления внутренних форм деталей. Их осуществляют двумя или тремя плоскостями, каждую из которых располагают параллельно координатной плоскости. Чаще всего секущие плоскости совпадают с плоскостями симметрии детали и соответствуют плоскостям разрезов, выполненных на чертеже детали. На аксонометрических проекциях не рекомендуется выполнять полный разрез, так как при этом теряется наглядность изображения. Обычно вырезают одну четвертую часть детали. Угол, образованный секущими плоскостями, всегда должен быть видимым.

Для определения наклона линии штриховки в каждой плоскости сечений поступают следующим образом. Строят аксонометрические проекции квадратов, лежащих в координатных плоскостях XOY, XOZ,YOZ, причем стороны квадратов параллельны и лежат на координатных осях X, Y, Z. Линии штриховки наносят параллельно диагоналям квадратов (рисунок 11.21, 11.22).

Рисунок 11.21 Рисунок 11.22

На рисунках 11.23, 11.24 показано направление штриховки прямоугольной изометрической проекции, на рисунках 11.25, 11.26 – в прямоугольной диметрической проекции.

Видео:Как построить правильный шестиугольник.Скачать

Презентация по черчению на тему «Аксонометрия шестиугольника»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Черчение. 8 класс. Мазаева И.М. Изометрия и ДиметрияСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Аксонометрия шестиугольника. Этапы построения. Черчение 8 класс

Задание: Выполнить в рабочей тетради изометрию и диметрию шестиугольника, воспользовавшись следующими этапами построения

1. Развернуть тетрадный лист горизонтально

2. Провести центровые линии в верхней части тетрадного листа

3. Начертить окружность R25

4. Разделить окружность на 6 равных частей

5. Построить изометрическую и диметрическую проекции Способ построения по клеткам

6. Построение изометрической проекции шестиугольника. Замеряем радиус и откладываем на оси ОХ точки 1 и 4

7. Замеряем расстояние от центра до стороны 2, 3 и откладываем на оси ОУ

8. Проводим параллельные линии через полученные точки

9. Замеряем половину стороны 2,3 и откладываем это расстояние на изометрической проекции

10. Соединить полученные точки

11. Строим диметрическую проекцию шестиугольника. Замеряем радиус и откладываем на оси ОХ точки 1 и 4

12. Для построения диметрической проекции шестиугольника необходимо найти середину расстояния от центра до стороны 5,6 (2,3) и отложить полученную величину на оси ОУ

13. Проводим параллельные линии и откладываем точки 2,3,5,6

13. Соединить полученные точки

Домашнее задание: Выполнить изометрию и диметрию треугольника (R25)

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 490 771 материал в базе

Материал подходит для УМК

«Черчение», Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С

7. Построение аксонометрических проекций

Видео:Как построить шестиугольник вписанный в окружностьСкачать

Дистанционные курсы для педагогов

Другие материалы

13.06.2020
1293

12.06.2020
813

12.06.2020
1551

08.06.2018
2040

06.06.2018
1529

08.05.2018
350

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

03.12.2020 1647 —> —> —> —>
PPTX 7.5 мбайт —> —>
Оцените материал:

Настоящий материал опубликован пользователем Плотникова Алена Павловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 6 лет и 1 месяц
Подписчики: 0
Всего просмотров: 18273
Всего материалов: 31

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Как начертить ПРИЗМУ ШЕСТИГРАННУЮ в объемеСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Ускоренный просмотр онлайн-лекций не мешает их пониманию

Время чтения: 3 минуты

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Регионы запустили работу по капремонту школ

Время чтения: 1 минута

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

Пандемия позволила детям получить больше внимания со стороны родителей

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.