Серединный перпендикуляр к хорде окружности

Видео:8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

Определение хорды

Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности

Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .

Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.

Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.

Видео:Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать

Свойства хорды к окружности

• Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
• Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
• Наибольшая возможная хорда является диаметром
• Серединный перпендикуляр к хорде проходит через центр окружности

• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу

• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
• Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Свойства хорды и вписанного угла

Видео:Геометрия 8 класс (Урок№30 - Свойство серединного перпендикуляра.)Скачать

Свойства хорды и центрального угла

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Формулы нахождения хорды

Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде

Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.

Видео:Серединный перпендикуляр. 7 класс геометрия. Центр описанной окружности треугольникаСкачать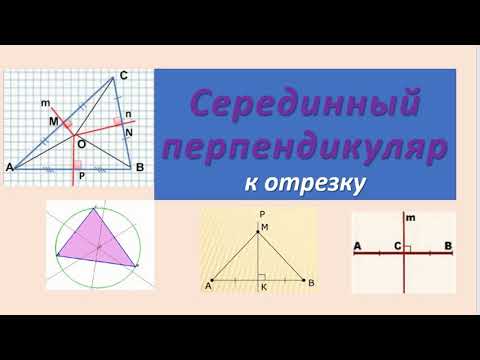

Решение задач

Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.

Задача.

Решение.

Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x

Согласно свойству хорд AS x SB = CS x SD, тогда

2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10

Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10

Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то

3,5х + 5,5х + 3х = 360
12х = 360
х = 30

Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165

Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:

90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5

Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Докажите, что серединный перпендикуляр к хорде окружности проходит через ее центр?

Геометрия | 5 — 9 классы

Докажите, что серединный перпендикуляр к хорде окружности проходит через ее центр.

Можно с рисунком, пожалуйста.

1) Диаметр, перпендикулярный хорде, делит ее пополам.

2) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.

3) Серединный перпендикуляр к хорде проходит через центр окружности.

4) Равные хорды удалены от центра окружности на равные расстояния.

5) Хорды окружности, удаленные от центра на равные расстояния, равны.

6) Окружность симметрична относительно любого своего диаметра.

7) Дуги окружности, заключенные между параллельными хордами, равны.

8) Из двух хорд больше та, которая менее удалена от центра.

9) Диаметр есть наибольшая хорда окружности.

2. Замечательное свойство окружности.

Геометрическое место точек M, из которых отрезок AB виден под прямым углом (AMB = 90°), есть окружность с диаметром AB без точек A и B.

3. Свойство серединных перпендикуляров к сторонам треугольника.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.

4. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.

5. Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы.

Это нужно запомнить и знать.

Окружность симметрична относительно центра и относительно любого своего диаметра.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Докажите , что диаметр окружности , проходящий через середину хорды , перпендикулярен хорде ?

Докажите , что диаметр окружности , проходящий через середину хорды , перпендикулярен хорде .

Видео:Геометрия. 8 класс. Урок 10 "Серединный перпендикуляр как ГМТ. Описанная окружность"Скачать

Докажите что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде?

Докажите что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

1) из точки О, являющейся центром окружности, на хорду СЕ опущен перпендикуляр ОМ?

1) из точки О, являющейся центром окружности, на хорду СЕ опущен перпендикуляр ОМ.

Докажите, что точка М является серединой хорды.

2)Проведите в окружности 2 диаметра MN и DF.

Докажите, что хорды MD и NF равны.

3)Дано : О — центр окружности, АВ = DC Доказать : угол АОВ = углу DOC.

Видео:Урок 12. Серединный перпендикуляр к отрезку (7 класс)Скачать

Докажите , что диаметр окружности, проведенный через середину хорды(не является диаметром), перпендикулярен этой хорде?

Докажите , что диаметр окружности, проведенный через середину хорды(не является диаметром), перпендикулярен этой хорде.

Видео:Теорема о диаметре и хордеСкачать

Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности?

Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Помогите пожалуйста?

1. Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности.

2. Докажите, что хорда перпендикулярная диаметру, делится диаметром на равные отрезки.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Докажите что перпендикуляры опущенные из цнтра окружности на две равные хорды равны между собой?

Докажите что перпендикуляры опущенные из цнтра окружности на две равные хорды равны между собой.

О — центр окружности AB и CD — хорды.

Видео:Геометрия 7класс Тема 14. Серединный перпендикуляр к отрезкуСкачать

Докажите что прямая содержащая середины двух параллельных хорд окружности проходит через ее центр?

Докажите что прямая содержащая середины двух параллельных хорд окружности проходит через ее центр.

Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Докажите , что прямая, содержащая середины двух параллельных хорд окружности , проходит через её центр?

Докажите , что прямая, содержащая середины двух параллельных хорд окружности , проходит через её центр.

Видео:Построение окружности по трём точкам.Скачать

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополамПОМОГИТЕ?

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополам

Вы открыли страницу вопроса Докажите, что серединный перпендикуляр к хорде окружности проходит через ее центр?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Радиусы и хорда образуют равнобедренный прямоугольный треугольник, в котором хорда — гипотенуза, найдем ее по теореме Пифагора √5 ^ 2 + 5 ^ 2 = √50 = 5√2.

Меньшая сторона — х Большая сторона — 4х х + х + 4х + 4х = 60 10х = 60 х = 6 4х = 24 Меньшая сторона = 6 Большая сторона = 24.

1)а, думаю верно, тип наколнная — это гипотенуза прямоугольного треугольника, которая образовалась с помощью наклонной, и её проекцией, и этот треугольник будет равнобедренным прямоугольным треугольником, ну и типо sin45 = a / c sqrt(2) / 2 = a / 24 ..

AA1 = СС1 ; AC = AA1 — CA1 ; A1C1 = CC1 — CA1 Тогда, АС = А1С1 ВС = В1С1(по условию), треугльники прямоугольные ΔАВС = ΔА1В1С1 — по двум катетам.

Дана трапеция ABCD : угол A = 68 угол D = 71 т. К. углы A, B односторонние , их сумма равна 180. Отсюда следует , что B = 180 — A = 112 углы C, D тоже односторонние , отсюда следует , что С = 180 — D = 109 /.

Повторяю ответ : Плоскость α параллельна прямой АВ, значит она пересекает стороны СА и СВ по прямой, параллельной АВ, то есть прямая EF параллельна прямой АВ. Тогда по теореме Фалеса СF : FB = CE : EA. СF : CB = 3 : 11, значит СF : FB = 3 : (11 — 3..

Решение во вложении, номер 12.

Значит есть формула d ^ 2 = a ^ 2 + b ^ 2 + c ^ 2 где d — диагональ a, b, c — высота, ширина и длина отсюда высота(c) равна c ^ 2 = d ^ 2 — a ^ 2 — b ^ 2 c ^ 2 = 49 — 4 — 9 = 36 c = 6 Площадь боковой поверхности равна сумме боковых граней т. Е. S = ..

1 задание : 1) да 2) нет 3) да 4) да 2 задание : угол А = 45 градусов угол В = 45 градусов угол М = 90 градусов.

🎦 Видео

Серединный перпендикуляр отрезкаСкачать