Считаем треугольники внутри треугольника

Школьные олимпиады — это не просто проверка знаний по пройденным темам. Это стимул изучать предметы шире и глубже, чем требуется по программе. Математика во втором классе еще не делится на алгебру и геометрию.

Геометрии во втором классе нет, но с основными геометрическими фигурами второклассники уже знакомы. Если возникнут вопросы по основным геометрическим терминам, можно обратиться к сайту http://simple-math.ru/ по ссылке.
Поэтому практически всегда в олимпиадных заданиях есть блок геометрических задач. В частности, задания на подсчет фигур.
Рассмотрим самую простую задачу.

Видео:Сколько треугольников на картинке? Расскажу, как посчитать это за 7 секунд!Скачать

Задача №1.

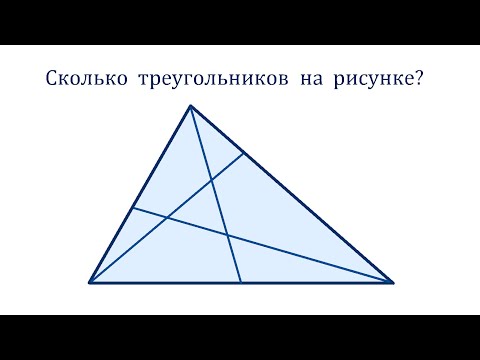
Сколько треугольников изображено на рисунке.

Есть три варианта рисунков — а, б, в.

Такого плана задания обычно не вызывают проблем, но все-таки разберем их, чтобы показать, как надо рассуждать при решении таких задач.

Рисунок А.

Обозначим уголки треугольника буквами A, B, C.

Проведем отрезок KL. Точка K лежит на на стороне треугольника AB, точка L лежит на стороне треугольника AC.

Был треугольник ABC. Добавился треугольник AKL.

Итого, получилось, что на рисунке всего 2 треугольника.

Рисунок Б.

Обозначим уголки треугольника буквами A, B, C.

Проведем отрезок KL. Точка K лежит на на стороне треугольника AB, точка L лежит на стороне треугольника AC.

Проведем отрезок NM . Точка N лежит на на стороне треугольника AB , точка M лежит на стороне треугольника AC.

Был треугольник ABC. Добавился треугольник AKL.

Добавился треугольник ANM .

Итого, получилось, что на рисунке всего 3 треугольника.

Рисунок В.

Решается аналогично. На рисунке 4 треугольника.

Видео:Способ сосчитать треугольники, которому не учат в школе! Сколько треугольников на картинке?Скачать

Задача №2.

Сколько треугольников изображено на рисунке?

Три варианта рисунков.

Начнем с самого простого.

Рисунок А

Обозначим уголки треугольника буквами A, B, C.

Проведем отрезок AL. Точка L лежит на стороне ВС.

Был треугольник ABC. Добавился треугольник ALB.

Добавился треугольник ALC .

Итого, всего стало 3 треугольника.

Рисунок Б

Обозначим уголки треугольника буквами A, B, C.

Проведем отрезок AL. Точка L лежит на стороне ВС.

Проведем отрезок AM . Точка M лежит на стороне ВС .

Получилось 6 треугольников.

Рисунок В

Добавился еще один отрезок, соответственно, добавились еще 4 треугольника. Всего 10 треугольников.

Давайте пересчитаем еще раз. Можно не давать названия треугольникам, а красить их. Вот так:

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Задача №3

Сколько четырехугольников изображено на рисунке?

Принцип решения задачи точно такой же, как и с треугольниками. мы можем рассуждать, задав каждой точке на рисунке свое буквенное имя.

Но для детей проще воспользоваться способом окраски.

Вариант А

Всего 3 четырехугольника.

Вариант Б

Всего 6 четурехугольников.

Вариант В

Всего 10 прямоугольников.

Видео:Сколько треугольников на рисунке? Универсальный алгоритм решения задачиСкачать

Задача №4

Сколько прямоугольников изображено на рисунке?

Решение:

Можно воспользоваться методом раскраски, как в предыдущей задаче.

А можно перечислить все прямоугольники по буквенному обозначению.

ABKL, ACHL, ADGL, AEFL — прямоугольники, начиная с первого перечислены.

BCHK, BDGK, BEFK — прямоугольники, начиная со второго перечислены.

CDGH, CEFH — прямоугольники, начиная с третьего перечислены.

DEFG — прямоугольники, начиная с четвертого перечислены.

Итого: 4 + 3 + 2 + 1 = 10

Всего 10 прямоугольников.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Задача №5

Сколько квадратов изображено на рисунке.

Подсчет ведем по количеству клеток-квадратиков в большем квадрате.

Начнем с варианта а.

Вариант А

В квадрате 4 клеточки, плюс сам квадрат

Итого 5 квадратов.

Вариант Б

Воспользуемся методом раскраски.

В квадрате 9 маленьких квадратиков, плюс сам квадрат, плюс 4 квадрата по 4 клетки.

Итого 14 квадратов.

Вариант В

Одноклеточных квадратов — 16 (4 ряда по 4 клетки в ряд )

Четырехклеточных квадратов — 9 (3 по 3)

Трехклеточных квадратов 4 (2 по 2).

Четырехклеточный квадрат 1.

16 + 9 + 4 + 1 = 30

Ответ: 30 квадратов.

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо.

Видео:Сколько треугольников на рисунке? Простая задача, которая позволяет загрузить даже студентовСкачать

Считаем треугольники — разбор задания

Неделю назад дал ученикам своих мини-групп задание посчитать все треугольники, из которых состоят два рисунка:

Легкий треугольник

Сложный треугольник

Задание 1.

К выполнению подобных заданий нужно подходить системно. (Именно этому я учу детей, которые собираются поступать в 5 класс математических гимназий и лицеев, на моем математическом кружке и в мини-группах в Новых Черемушках.)

Пронумеруем все элементы легкого треугольника.

Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.

1. Из 1 элемента: 1, 2, 3, 5 — всего 4 треугольника (некоторые дети автоматически зачисляют в треугольники элементы № 4 и № 6 — это неправильно!).

2. Из 2 элементов: 12, 34, 56, 13, 35, 24 — всего 6 треугольников.

3. Из 3 элементов: 135, 246 — 2 треугольника.

4. Из 4 элементов: 1234 и 3456 — 2 треугольника.

5. Из 5 элементов — ничего нет.

6. Из 6 элементов — единственный 123456.

Итого: 15 треугольников.

Задание 2.

Сложное задание, требующее от детей внимательности, усидчивости и аккуратности в подсчетах. Пронумеруем все элементы легкого треугольника, причем цифр от 1 до 9 нам не хватит. Задействуем 10, 11 и 12.

Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.

1. Из 1 элемента: все от 1 до 12 — это треугольники. Их 12 штук.

2. Из 2 элементов. Начинаем считать от вершины и движемся по часовой стрелке. 12, 17, 18, 9 11, 11 12, 12 10, 56, 54, 43. Не забудем про внутренние треугольники: 28, 9 10, 36. Насчитали снова 12 штук.

3. Из 3 элементов — отыщем их только во внутреннем треугольнике. 289, 36 10, 823, 9 10 6, 10 98, 632. Их 6 штук.

4. Из 4 элементов: 1234, 1236, 789 10, 789 11, 12 10 63, 12 10 65, 289 11, 4328, 56 10 9. Набрали еще 9 треугольников.

5. Из 5 элементов — ничего не нашел. Кто найдет — напишите, объявлю благодарность.

6. Из 6 элементов: 123456, 789 10 11 12, 12789 11, 12 10 6345, 56 10 9 11 12, 432178 — нарыли еще 6 штук. Плюс центральный: 236 10 98. Итого — 7 треугольников.

7. Ну и самый большой, из 12 элементов — 1 треугольник.

Кратко:
1 — 12
2 — 12
3 — 6
4 — 9
6 — 7
12 — 1

Итого: 47 треугольников. (Огромное спасибо мамам Антона и Маруси, которые помогли мне найти недостающие треугольники из 4-х элементов).

Бедные мои ученики…

Сочувствую. Но если им нужно сдавать вступительные экзамены в наши математические школы Юго-Запада (1533, 1534, 1543, 2007, Л2Ш, 1514 и т.д.) или участвовать в олимпиадах, то такая тренировка мозгов пойдет им только на пользу.

Так что их ждут новые задания. Что-то — полегче, что-то — потяжелее. Поступление в хорошую школу стоит того, чтобы усердно работать над заданиями, чуть-чуть выходящими за рамки школьной программы.

Видео:Сколько треугольников вы видите на рисункеСкачать

Задачи «на подсчет треугольников»

5.3.2. Опишем проведенную работу при решении задач «на подсчет треугольников». В первых геометрических задачах будет применяться термин «взаимопроникающие фигуры», предложенный И.С. Якиманской. Вслед за ней взаимопроникающими мы называем такие фигуры, которые имеют часть общей площади: одними своими частями они перекрывают друг друга, другими частями не совпадают [196].

Посмотрите на рис. 5.2, а: треугольник АВС можно разделить на составляющие его фигуры: треугольники АЕО, О DC, АОС и четырехугольник BEOD (рис. 5.2, б).

Можно рассмотреть и другие имеющиеся в треугольнике АВС треугольники: ABD, ЕВС, АЕС, ADC (рис. 5.2, в). В этом случае мы получаем «взаимопроникающие» фигуры.

Исследование И.С. Якиманской [196] было направлено на изучение того, как учащийся анализирует геометрический чертеж, какие фигуры выступают для него более явно, бросаются в глаза, а какие трудны для выделения, на что опирается учащийся при рассмотрении чертежа, какие умственные процессы обеспечивают возможность различного видения чертежа. Результаты, полученные И.С. Якиманской, очень интересны, к сожалению, их недостаточно используют при работе с учащимися.

Задачи с взаимопроникающими элементами использовал в своей работе и В. А. Крутецкий. С помощью этих задач он исследовал особенности аналитико-синтетического восприятия геометрических фигур учащимися, в частности умения рассматривать и оценивать взаимопроникающие элементы геометрических фигур с различных точек зрения, выделять элементы фигур и фигуры из фона, включать один и тот же элемент в разные фигуры и соответственно давать им различную интерпретацию.

Рассмотрим некоторые задачи по подсчету треугольников с учетом взаимопроникающих фигур.

Задача 5.8. Сколько отрезков вы видите на рис. 5.3? Назовите их.

Задача 5.9. Сколько треугольников изображено на рис. 5.4? Назовите их.

Задача 5.10. Сколько углов вы видите на рис. 5.5? Назовите их.

В.А. Крутецкий ограничивал исследование тем, что фиксировал, «насколько полный ответ дают испытуемые, какую роль играют „видение» и „рассуждение»» [98].

Учитывая вышеизложенное, рассмотрим, как можно использовать «цепочки задач на подсчет треугольников» для выявления «геометрического зрения», уровней владения приемами анализа и синтеза, алгоритмических способностей учащихся, причем не будем ограничиваться только окончательным ответом, а приведем качественный анализ выполнения задания.

Б.М. Теплов подчеркивал, что «не следует вовсе исключать возможность количественного подхода при исследовании способностей. Он возможен, однако, только в том случае, когда он следует за качественным анализом, вытекает из него, им определяется» [171].

Количественная характеристика применялась нами при оценке:

• • геометрического зрения — насколько полно и точно учащийся увидел искомые фигуры; количество выделенных фигур из фона;
• • аналитико-синтетической деятельности — наличие и количество «идей» при решении задач, выбор наиболее рационального способа решения;
• • алгоритмические способности — количество шагов, приводящих к правильному решению.

Ниже приведены некоторые из предлагаемых учащимся заданий по подсчету треугольников и дан анализ их решения.

Задача 5.11. Сосчитайте, сколько треугольников изображено на рис. 5.6.

Цепочка задач построена таким образом, что при переходе к каждой последующей фигуре увеличивается число искомых треугольников (принцип нарушается при переходе от слу-

чая 5.6, в к случаю, изображенному на рис. 5.6, г, но в случае 5.6, г усложняется «геометрический фон», т. е. появляются такие взаимопроникающие треугольники, которые состоят, например, из треугольника и четырехугольника, а в случае 5.6, в все взаимопроникающие треугольники можно рассматривать состоящими только из треугольников).

Оценка выполнения задания (а)

• 1. Если учащийся увидел на рис. 5.6, а большой треугольник, состоящий из двух маленьких, т. е. всего три треугольника, то он получает 1 балл.
• 2. Если учащийся не видит какой-либо из трех треугольников, то он получает 0 баллов.

Оценка выполнения задания (б)

На рис. 5.6, б изображен большой треугольник, состоящий из трех маленьких, всего четыре треугольника. Такое решение оценивается в 1 балл.

Схема рассуждений и ход решения (в)

1. Воспроизведем рис. 5.6, в. Пронумеруем треугольники (рис. 5.7, а). Сосчитаем все маленькие треугольники, их всего шесть (рис. 5.7, б).

• 2. Сосчитаем треугольники, состоящие из двух маленьких, их всего три (рис. 5.7, в).
• 3. Сосчитаем треугольники, состоящие из трех маленьких, их всего шесть (рис. 5.7, г).
• 4. Треугольник, состоящий из шести маленьких треугольников, — один (рис. 5.7, а).

Всего получилось 16 треугольников.

Оценка выполнения задания (в)

• 1. Учащиеся сосчитали (увидели) все взаимопроникающие треугольники, подсчет вели с помощью алгоритма — 2 балла.
• 2. Задача решалась без применения алгоритма (какие треугольники учащийся увидел, такие и сосчитал, но нашел больше семи треугольников — 1 балл).
• 3. Учащийся при решении насчитал меньше семи треугольников, т. е. не увидел взаимопроникающих треугольников, — оценка 0 баллов.

Схема рассуждений и ход решения (г)

• 1. Сосчитаем треугольники в «нижней» части рис. 5.6, г, их всего шесть, причем все они состоят только из треугольников (рис. 5.8, а, б, в).
• 2. Добавляем «верхнюю» часть, получаем треугольники, состоящие из треугольников и четырехугольника, решение аналогично решению в случае а, треугольников тоже шесть (рис. 5.9, а, б, в).

Всего получилось: (3 + 2 + 1) + (3 + 2+ 1) = 12 треугольников.

Оценка выполнения задания (г)

• 1. Учащийся подсчитал все треугольники с помощью алгоритма (выбор алгоритма значения не имеет) — оценка 3 балла.
• 2. Учащийся применил для решения алгоритм, не позволивший выделить все имеющиеся на рисунке треугольники — оценка 2 балла.
• 3. Учащиеся, сосчитавшие только треугольники на рис. 5.8, а, в и рис. 5.9, а, в, т. е. не увидевшие взаимопроникающих треугольников, получают 1 балл.

4. Учащиеся, увидевшие на рисунке меньше семи треугольников, получают О баллов.

Схема рассуждений и ход решения (д)

В этой задаче (как, впрочем, и в других) при подсчете числа треугольников без алгоритма есть опасность «потерять» треугольники, поэтому полезно обозначить треугольники цифрами (рис. 5.10).

• 1. Начнем подсчет с маленьких треугольников, их всего 12 (рис. 5.10).
• 2. Считаем треугольники, состоящие из трех маленьких (два маленьких треугольника образуют ромб), таких треугольников шесть (рис. 5.11).

3. Четыре, пять, шесть, семь, восемь маленьких треугольников не образуют новых треугольников, а треугольников, состоящих из девяти маленьких треугольников, — два (рис. 5.12).

Всего получилось 12 + 6 + 2 = 20 треугольников.

Оценка выполнения задания (д)

• 1. Учащиеся, предложившие алгоритм подсчета и сосчитавшие все треугольники, получают 3 балла.
• 2. Учащиеся, сосчитавшие все треугольники, но не предложившие алгоритм подсчета, получают 2 балла.
• 3. Учащиеся, увидевшие случаи, изображенные на рис. 5.11 и рис. 5.12, но пропустившие некоторые треугольники, получают 1 балл.
• 4. Учащиеся, не увидевшие случаи, изображенные на рис. 5.11, 5.12, получают 0 баллов.

Схема рассуждений и ход решения (е)

Эта задача самая сложная в цепочке, выявляющей «уровни видения» взаимопроникающих треугольников, так как в ней появляются треугольники, состоящие из треугольников и пятиугольника. Пронумеруем все элементы пятиугольника (рис. 5.13).

1. Десять маленьких треугольников (1-10) (рис. 5.13).

• 2. Десять треугольников, состоящих из двух маленьких треугольников (1-2, 2-3,
• 3-4, 4-5, 5-6, 6-7, 7-8, 8-9, 9-10, 10-1).
• 3. Пять треугольников, состоящих из трех маленьких треугольников (1-2-3,
• 3-4-5, 5-6-7, 7-8-9, 9-10-1).
• 4. Пять треугольников, состоящих из двух маленьких треугольников и пятиугольника (2-11-6, 4-11-8, 6-11-10, 8-11-2,10-11-4).
• 5. Пять треугольников, состоящих из четырех маленьких треугольников и пятиугольника (1-2-10-11-6, 3-4-2-11-8, 5-6-4-11-10,7-8-6-11-2,9-8-10-11-4).

Всего получилось 10 + 10 + 5 + 5 + 5 = 35 треугольников.

Оценка выполнения задания (д)

• 1. Учащийся увидел все взаимопроникающие треугольники, предложил алгоритм подсчета (не обязательно рассмотренный нами) — оценка 4 балла.
• 2. Учащийся увидел треугольники, соответствующие пп. 1, 2, 3, 4 или 1, 2, 3, 5 и какие-то треугольники, соответствующие пп. 4 или 5, — оценка 3 балла.
• 3. Учащийся увидел треугольники, соответствующие пп. 1, 2, 3, но не увидел ни одного треугольника, соответствующего пп. 4 и 5, — оценка 2 балла.
• 4. Учащийся увидел какие-то треугольники, соответствующие пп. 1, 2, 3, но не все — оценка 1 балл.
• 5. Учащийся увидел только треугольники, соответствующие п. 1, — оценка 0 баллов.

При рассмотрении предложенных в предыдущей задаче случаев видно, что можно пользоваться «методом проб и ошибок», но без подключения «анализа» (причем иногда довольно углубленного) успеха добиться трудно.

Задача 5.12. Сосчитайте, сколько треугольников изображено на рис. 5.14.

Ответ: на рис. 5.14, а изображено 13 треугольников; 5.14,6 — 27 треугольников; 5.14, в — 47 треугольников; 5.14, г —27 треугольников; 5.14, д — 32 треугольника; 5.14, е — 48 треугольников.

🎬 Видео

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

ВЫСОТА ТРЕУГОЛЬНИКА #shorts #математика #треугольник #высотатреугольника #геометрия #егэ #огэСкачать

Треугольники. 7 класс.Скачать

7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Где находится точка в треугольнике заданном координатами вершин, внутри или вне треугольника.Скачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Лайфхак про среднюю линию треугольника #геометрия #математика #бравлстарс #brawlstarsСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Сколько треугольников на рисунке?Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать